稳健的双基地MIMO雷达目标角度跟踪算法*

张正言,周青松,黄中瑞,徐旭宇

(1.电子工程学院,安徽 合肥　230037；2.中国人民解放军73677部队，江苏 南京　210016)



探测跟踪技术

稳健的双基地MIMO雷达目标角度跟踪算法*

张正言1,周青松1,黄中瑞1,徐旭宇2

(1.电子工程学院,安徽 合肥230037；2.中国人民解放军73677部队，江苏 南京210016)

摘要：针对双基地多输入多输出(MIMO)雷达变速目标角度跟踪问题，提出了基于变遗忘因子的跟踪算法。首先研究了遗忘因子对算法的收敛速率和跟踪性能的影响；其次借鉴变步长最小均方(LMS)算法的思路，提出遗忘因子的递推公式；最后将遗忘因子递推公式引入PASTd算法中，实现变速目标的收发角度跟踪。实验表明：算法的收敛速度和性能都有较大的提高，稳定性得到了增强。

关键词：双基地MIMO雷达；变速目标；角度跟踪；变遗忘因子；旋转不变子空间技术；紧缩近似投影子空间跟踪

0引言

近年来，多输入多输出(multiple-inputmultiple-output,MIMO)雷达作为一种新的雷达体制受到了广泛关注，与传统相控阵雷达不同的是，MIMO雷达能显著提高系统的目标检测、跟踪、识别和参数估计等性能[1]。在双基地MIMO雷达目标定位中，目标的发射角(DOD)和接收角(DOA)是需要被估计的主要参数[2-6]。但是当目标运动时，文献[2-7]中的算法性能会急剧下降甚至失效。目前大部分关于双基地MIMIO的文献都是针对目标静止的情况，不能适用于目标运动的情况，因为这类算法大多是基于子空间类算法，需要进行协方差矩阵的估计和分解，这就会出现2个问题：一是协方差矩阵的估计需要大量的快拍数，而目标运动时，接收的数据对应的角度在不同快拍数是不同的，大量的快拍数会造成目标角度的失真；二是协方差矩阵的估计与分解，运算量较大，不能够实时的给出目标位置，而运动目标位置是变化的，需要给出目标的实时位置，否则跟踪算法是没有意义的。

关于MIMO雷达角度跟踪的研究还处于起步阶段，文献[8]提出PARAFAC自适应算法并且应用到单基地MIMO雷达，成功实现了目标角度的跟踪。文献[9]简单的利用PASTd算法实现了双基地MIMO雷达角度的跟踪，但是上述算法需要额外的数据相关运算。文献[10]提出Kalman-PASTd算法，应用到单基地MIMO雷达中，能够实现自动相关运算。然而PARAFAC算法、PASTd算法和Kalman-PASTd算法都有较高的运算复杂度。文献[11]提出了一种适合单基地MIMO雷达的低复杂度角度跟踪算法，但是该算法只适用于单基地MIMO雷达，而双基地MIMO雷达的联合方向矢量更加复杂，文献[11]的算法不再适用。

文献[8-11]的算法只适合目标运动速度不变的情况，在PASTd算法中的遗忘因子是恒定的。PASTd算法基本思想是将RLS-like(recursiveleasesquare-like)算法应用到信号子空间跟踪中。在RLS算法中，遗忘因子λ在收敛性、精度和稳定性起到至关重要的作用，遗忘因子的取值范围在0～1，当遗忘因子接近1时，算法有较好的稳定性和跟踪性能，但是收敛速度较慢，跟踪能力较差；当遗忘因子降低时，收敛速度变快，跟踪能力加强，但是稳定性和跟踪性能变差。目前最小二乘变步长算法已经很成熟，有大量的变步长算法，变步长算法和变遗忘因子算法有相似之处。因此，为了解决RLS算法对遗忘因子要求的矛盾，本文借鉴LMS算法中变步长的思想，提出基于变遗忘因子的双基地MIMO雷达的角度跟踪算法。

1信号模型

假设双基地MIMO雷达收发阵元均是均匀分布的，收发阵元个数为N和M个，阵元间距dt和dr为波长λ的一半。双基地MIMO雷达的配置如图1所示。

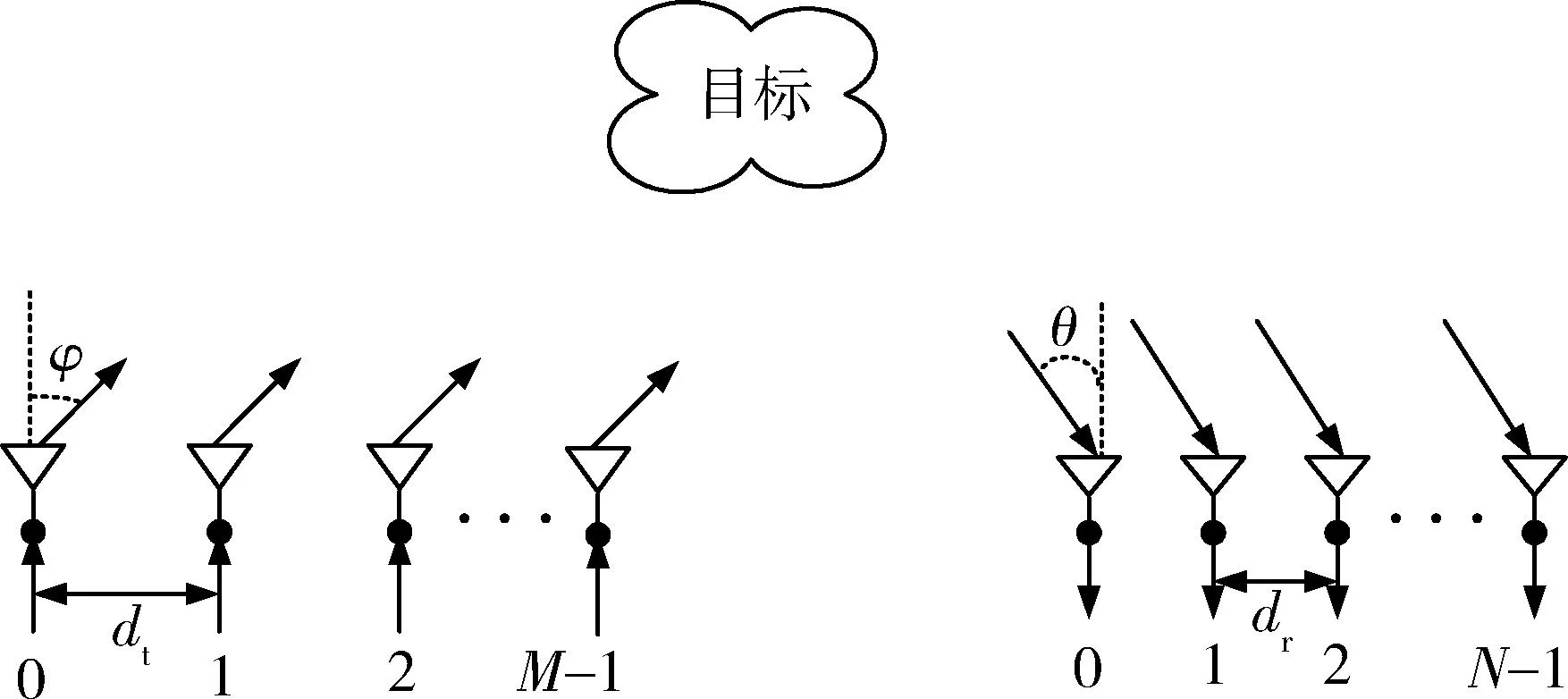
图1　双基地MIMO雷达收发阵元配置Fig.1　Arrays configuration of bistatic MIMO radar transceiver

假设有P个远场运动目标，假设目标是非相干的，在t时的目标的收发角度为[(θt,1,φt,1),(θt,2,φt,2),…，(θt,P,φt,P)]，则到达第N个接收阵元的信号为

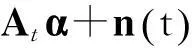
(1)

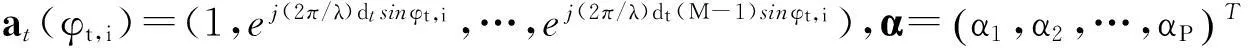
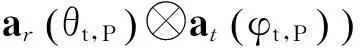
(2)

2算法描述

2.1遗忘因子的递推公式

首先，考虑目标运动过程中速度发生变化的情况，即目标角度变化速率不能再看做恒定时。当遗忘因子固定时，只对某一运动速度具有较好的跟踪性能，对于其他速率的跟踪性能较差。文献[12]已经证明LMS变步长方法中的步长与RLS算法中的1-λ的作用相同，文献[13]已经成功将变步长的思想应用到了RLS算法中，因此，本文将变步长的思想应用到PASTd算法中。在LMS算法中，有如下的变步长策略：

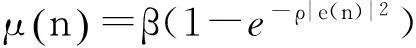
(3)

式中：β为最大步长;ρ为控制μ(n)形状的参数；e(n)为误差;e(n)的变化用来控制步长的变化。

由于u(n)与1-λ(n)的作用相同，不妨设u(n)=1-λ(n)，则λ(n)=(1-β)+βe-ρ|e(n)|2=λmin+(1-λmin)e-ρ|e(n)|2，

(4)

由于β是最大步长，所以λmin=1-β，λmin为极小遗忘因子。

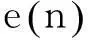
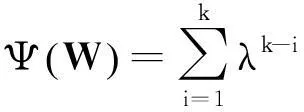
(5)

式中：y(k)=WH-(k-1)x(k)。

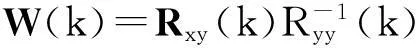
Rxy(k)=λRxy(k-1)+x(k)yH-(k)，

(6)

Ryy(k)=λRyy(k-1)+y(k)yH-(k).

(7)

由先验信息得到估计误差

e(k)=x(k)-W(k-1)y(k)，

(8)

式中：x(k)为当前接收到的数据；W(k-1)为满足上一时刻代价函数最小的子空间，当信号角度变化速率小时，误差e(k)小，当信号角度变化速率大时，误差e(k)变大。信号角度速率变化大时，需要相对较小的遗忘因子提高收敛速度，提高跟踪能力。信号角度速率变化较小时，需要相对较大的遗忘因子提高跟踪的性能和稳定性。可以看出PASTd算法中的误差e(k)与式(4)中的e(n)作用相同，因此可以用e(k)代替e(n)。式(4)计算较复杂，用2代替e作为底数，对其改进得到PASTd算法的遗忘因子递推公式：

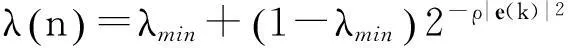
(9)

从式(9)中可以看出，当目标角度变化速率增大时，e(k)的模值增大，λ(n)接近于极小值λmin，保证收敛速度，当目标角度变化速率减小时，e(k)的模值减小，λ(n)接近于1，保证算法的性能。ρ是一个参数，控制系统敏感度。

在开始跟踪的初始阶段，或者当目标运动速度相对较大时，称为目标位置发生突变，这时系统处于不稳定状态，算法未收敛，误差e(k)极大，式(9)中的极小值λmin无法满足此时的收敛速度要求，需要设置一个最小的遗忘因子λzmin。下面给出这种情况下的遗忘因子选取策略：

If|e(k)|2>δ

λ(n)=λzmin

(10)

End

式中：δ为门限，当误差的模值大于δ，认为此时系统处于不稳定状态，选取遗忘因子等于最小值λzmin，加快收敛速度，使系统尽快进入稳定状态。

2.2PASTd算法

在PASTd算法中，信号子空间可以通过最小化下面的目标函数得到：

tr(C(t))-2tr(WH(t)C(t)W(t))+

tr(WH(t)C(t)W(t)WH(t)W(t))，

(11)

在1≤i≤t内的所有数据都被用来估计时刻t的信号子空间，当目标运动时，λ用来确定时刻t之前数据的权重，能够更好地满足跟踪要求，提高跟踪效果。

可以采用快速递归最小二乘法求解目标函数的最小值，当信号处于慢变或静止时，W(i)r(i)可以和W(i-1)r(i-1)非常接近，算法收敛。

下面给出PASTd算法的具体步骤：

Fort=1:Ns

x1(t)=r(t)

(12)

Fork=1:P

(13)

βk(t)=λβk(t-1)+|yk(t)|2

(14)

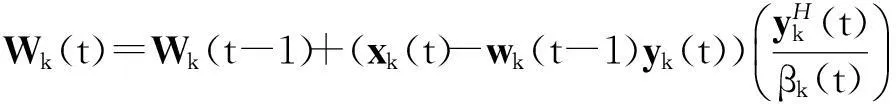
(15)

xk+1(t)=xk(t)-Wk(t)yk(t)

(16)

Endfor

Endfor

可以证明由W(i)张成的信号子空间与Us(t)张成的信号子空间相同，即span{W(t)}=span{Us(t)}，因此可以通过PASTd算法获得信号子空间，避免了互相关矩阵的特征值分解，减小了大量的计算量，因此PASTd算法适合跟踪运动目标的DOD和DOA。

2.3基于变遗忘因子的改进算法

把变遗忘因子递推公式引入到PASTd算法中，将改进后的PASTd算法归纳如下：

Fort=1:Ns

x1(t)=y(t)

(17)

Fork=1:K

(18)

βk(t)=λ(t-1)βk(t-1)+|yk(t)|2

(19)

e(t-1)=xk(t)-wk(t-1)yk(t)

(20)

(21)

xk+1(t)=xk(t)-Wk(t)yk(t)

(22)

If|e(k)|2>δ

(23)

else

λ(t)=λmin+(1-λmin)2-ρ|e(t-1)|2

(24)

End

Endfor

Endfor

2.4正交化过程

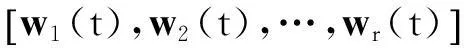
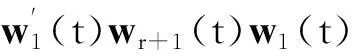
(25)

wr+1(t)=v/‖v‖，

(26)

通过上面的步骤得到了信号子空间W(t)。

2.5收发角度的估计及配对

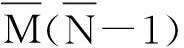
Ur2=Ur1Ψr.

(27)

对Ψr特征值分解得到Φr，Φr包含所有的DOA的信息[14]，

Ψr=T-1ΦrT.

(28)

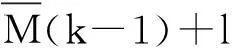
Ut2=Ut1Ψt,

(29)

对Ψt特征值分解得到Φt，Φt包含所有的DOD的信息，

Ψt=T-1ΦtT.

(30)

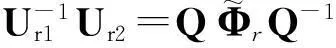
(31)

根据式(28)与式(31)可以看出Q，T-1与Ψr的特征向量是线性关系[15]，所以

Q=T-1F,

(32)

式中：F为变换矩阵。将式(32)代入(31)，与式(28)比较得

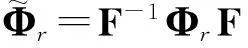
(33)

构造如下矩阵

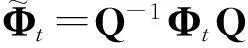
(34)

并将式(30)和式(32)代入式(34)得

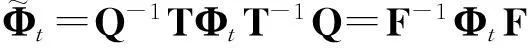
(35)

至此，完成了目标收发角度的自动配对，通过式(36)获得配对后的收发角

(36)

式中：angle为去相运算；p=1,2,…，P。

2.6算法流程

步骤1使用变遗忘因子算法中式(17)～(24)得到特征向量矩阵W；

步骤2利用2.4节式(25)和式(26)进行正交化；

步骤3根据2.5节ESPRIT算法得到包含目标收发角度的对角矩阵Φr和Φt，由配对方法进行自动配对，由式(36)得到收发角度；

步骤4重复步骤1～4估计下一时刻的角度。

3实验仿真及结果分析

双基地MIMO雷达收发阵元分别为N=5和M=8，噪声为高斯加性白噪声，目标位远场目标。定义

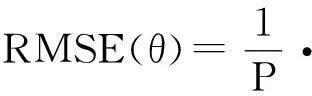
实验1：验证算法的有效性

假设空中存在一个目标，在前30s目标每秒变化1°，且在30s时发生突变，后30s内目标角度每秒变化速率降低，信噪比为SNR=10dB，误差e(k)的模值和遗忘因子如图2所示。

从图2a)可以看出，在开始跟踪的初始阶段，和t=30s时，目标角度发生突变时，误差变大，且超过了门限δ，系统处于不稳定状态，此时需要最小的遗忘因子λzmin，增加收敛速度，使系统处于稳定状态。在前30s内信号角度变化较快，此时误差较大且不稳定，需要极小遗忘因子，后30s内信号角度变化较慢，误差较小且相对稳定，需要相对较大的遗忘因子。图2b)可以看出在开始跟踪和信号角度处于突变阶段，遗忘因子等于最小值λzmin，前30s内遗忘因子相对较小，而后30s内遗忘因子相对较大，符合遗忘因子选取原则，验证了算法的有效性。

空中存在一个目标，在前30s目标每秒变化1°，后30s内目标角度每秒变化速率降低，信噪比为SNR=10dB，本文算法与文献[8]算法(Wu-Method)仿真结果如图3所示。

从图3可以看出在前30s内本文算法性能比Wu-Method性能要好，后30s内本文算法与Wu-Method性能相当。在t=30s时，本文算法有效，而Wu-Method跟踪性能较差，基本失效。这是因为Wu-Method的遗忘因子固定为0.97，适合慢速运动的目标，所以后30s目标运动较慢时，性能略好，而当前30s目标运动速度快时。Wu-Method跟踪性能低于本文算法，本文算法是根据运动速度选取遗忘因子，能够适应于目标速度的变化，特别是信号角度

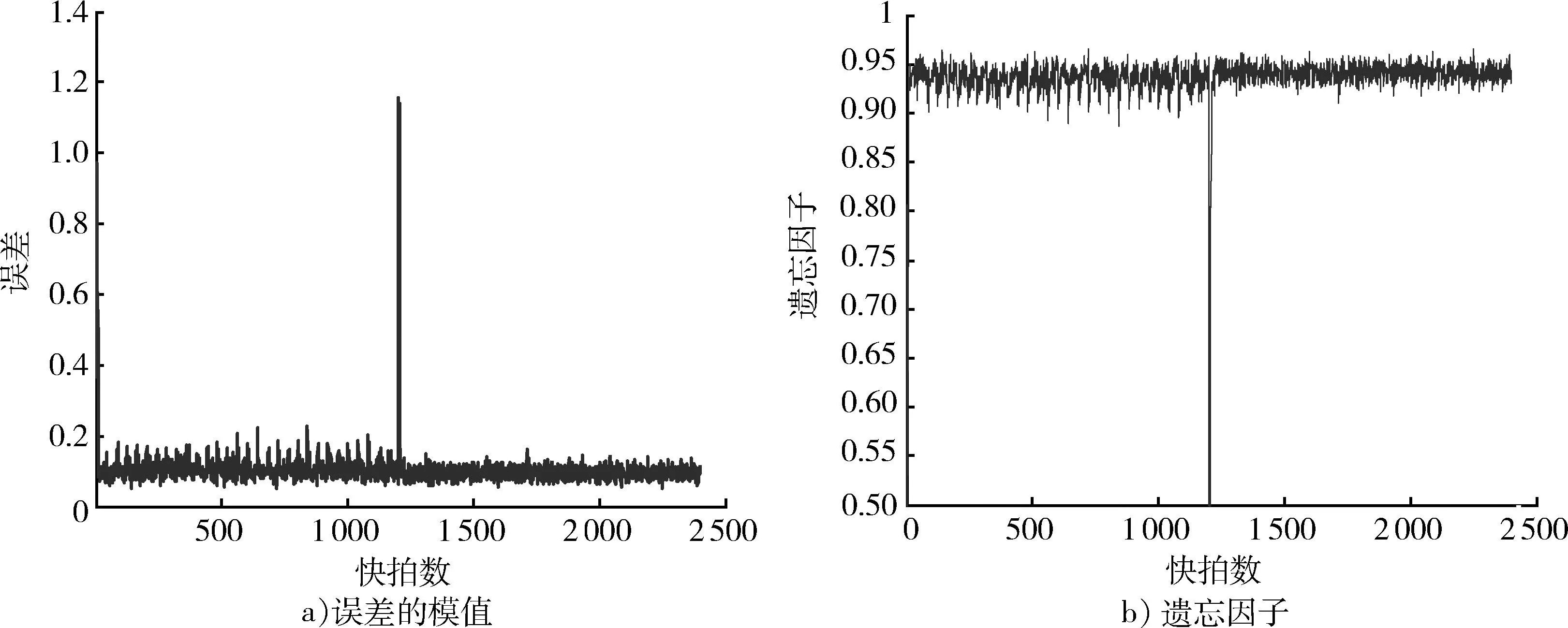
图2　误差和遗忘因子随快拍数的变化Fig.2　Error and forgetting factor along with the number of snapshots

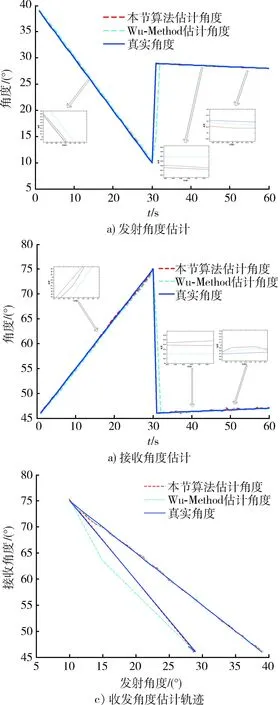
图3　目标角度跟踪Fig.3　Target angle tracking

突变时，Wu-Method的算法基本失效，而本文算法仍然有效，实验结果验证算法的有效性。多目标时本文算法仍然有效，因为文中的算法是改变PASTd算法中的遗忘因子，PASTd算法能够解决多目标角度跟踪问题，变遗忘因子递推公式是针对误差的变化，多目标时时针对整体误差的变化，对单个目标可能不是最佳的遗忘因子，但是对整体目标是最佳的。PASTd算法在目标运动相交时跟踪精度变低，可以结合经典的数据关联算法如卡尔曼预测算法[10]，解决目标运动相交的问题。因此本文算法在多目标时仍然有效，跟踪性能较好，稳健性较强。

实验2：算法的RMSE随信噪比的变化

信噪比SNR=0～15dB，F=500，其余条件与实验1相同，算法性能的仿真结果如图4所示。

从图4中可以看出本文算法的RMSE随着信噪比的增大而减小，在信噪比相同的情况下，本文算法的性能明显高于Wu-Method，Wu-Method已基本失效，说明了本文算法能够成功跟踪变速运动目标的角度。

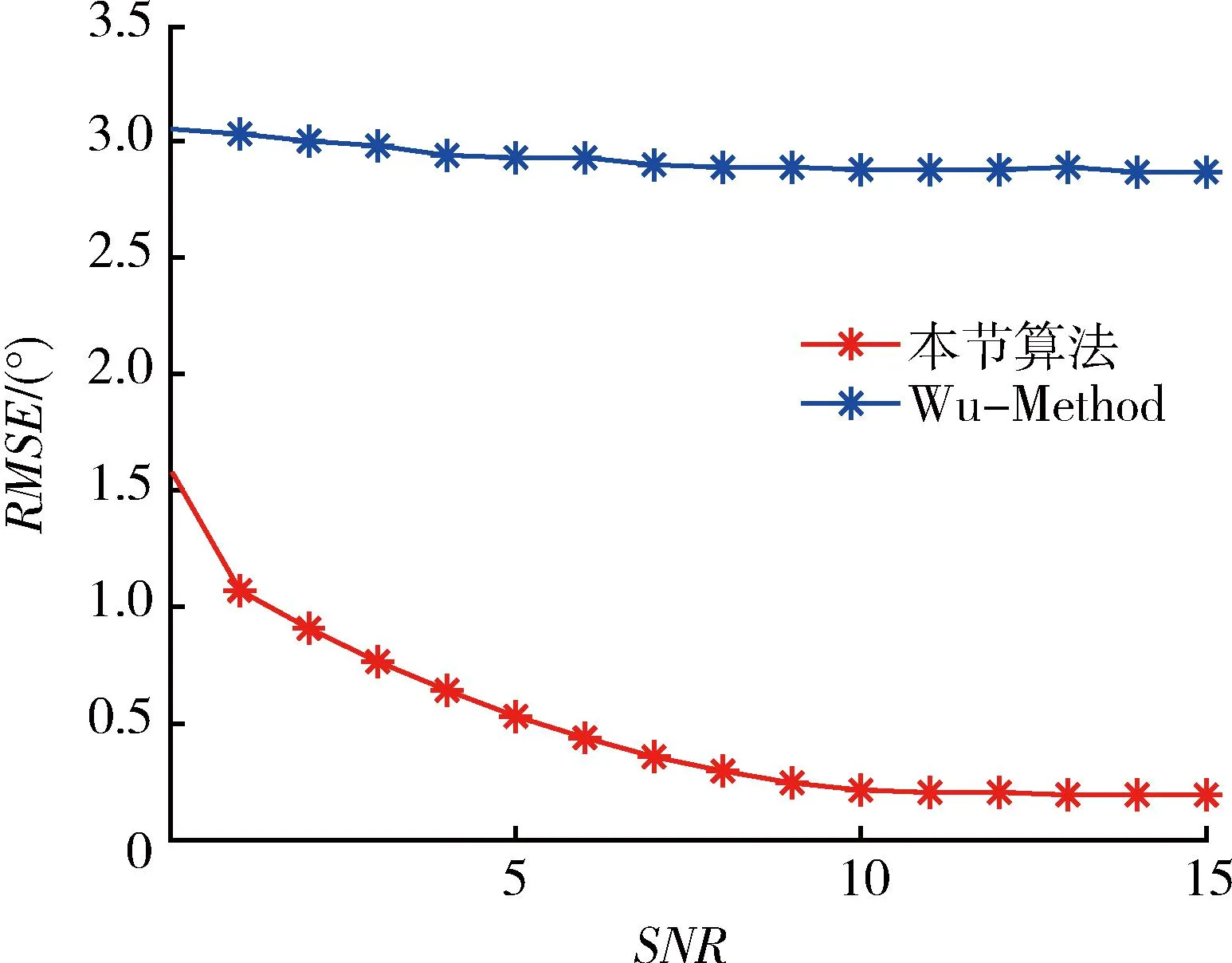
图4　RMSE与信噪比的关系Fig.4　Change of RMSE along with signal-to-noise ratio

4结束语

本文研究了变速目标条件下双基地MIMO雷达目标角度跟踪问题。首先分析了遗忘因子对于跟踪算法的影响，借鉴LMS变步长算法的思想，应用到双基地MIMO雷达目标角度跟踪中，提出基于变遗忘因子的方法。首先针对目标速度变化时，推导了遗忘因子的递推公式，然后考虑跟踪开始和目标角度发生突变时的情况，提出判别方法，将遗忘因子变为最小值，加快收敛速度，使跟踪系统尽快进入稳定状态。本文算法的遗忘因子可以随着目标的运动情况发生改变，能够自适应目标的速度变化，具有较好的跟踪速度和跟踪性能，在跟踪的初始阶段和目标角度发生突变时，本文算法的遗忘因子可以变为预设的最小遗忘因子，可以使系统最快的进入稳定状态，快速跟踪目标的角度。

参考文献：

[1]陈浩文, 黎湘, 庄钊文. 一种新兴的雷达体制——MIMO雷达[J]. 电子学报，2012, 40(6)：1190-1198.

CHENHao-wen,LIXiang,ZHUANGZhao-wen.ARisingRadarSystem——MIMORadar[J].ActaElectronicaSinica, 2012, 40(6): 1190-1198.

[2]ZHENGGui-mei,CHENBai-xiao,YANGMing-lei.UnitaryESPRITAlgorithmforBistaticMIMORadar[J].ElectronicsLetters, 2012, 48(3): 179-181.

[3]XIERong,LIUZheng,WUJian-xin.DirectionFindingwithAutomaticPairingforBistaticMIMORadar[J].SignalProcessing, 2012, 92(1): 198-203.

[4]YANH，LIJ,LIAOG.MultitargetIdentificationandLocalizationUsingBistaticMIMORadarSystems[J].EURASIPJournalonAdvancesinSingalProcessing, 2008, 8(2): 1-8.

[5]郑志东, 张剑云. 基于ESPRIT的MIMO雷达测向方法[J]. 雷达科学与技术，2009, 7(3)：205-209.

ZHENGZhi-dong,ZHANGJian-yun.DirectionFindingBasedonESPRITinMIMORadar[J].RadarScienceandTechnology, 2009, 7(3)：205-209.

[6]张剑云, 郑志东, 李小波. 双基地MIMO雷达收发角及多普勒频率的联合估计算法[J]. 电子信息学报，2010, 32(8)：1843-1848.

ZHANGJian-yun,ZHENGZhi-dong,LIXiao-bo.AnAlgorithmforDOD-DOAandDopplerFrequencyJointlyEstimationofBistaticMIMORadar[J].JournalofElectronics&InformationTechnology, 2010, 32(8)：1843-1848.

[7]CHENYM.OnSpatialSmoothingforTwo-DimensionalDirection-of-ArrivalEstimationofCoherentSignals[J].IEEETransactionsonSignalProcessing, 1997, 45 (7): 1689-1696.

[8]WUH,ZHANGX.DOATrackinginMonostaticMIMORadarUsingPARAFAC-RLSTAlgorithm[C]∥Proceedingsofthe3rdInternationalConferenceonInformationandSystemsEngineering(ICISE’11)：958-961.

[9]WUHL,ZHANGXF.DODandDOATrackingforBistaticMIMORadarUsingPASTdWithoutAdditionalAnglesPairing[C]∥IEEEFifthInternationalConferenceonAdvancedComputationalIntelligence, 2012：1132-1136.

[10]ZHANGXF,LIJF,FENGGP,etal.Kalman-PASTdBasedDOATrackingAlgorithmforMonostaticMIMORadar[C]∥InternationalConferenceonInformation,ServicesandManagementEngineering, 2011：220-224.

[11]YUHX,ZHANGXF,CHENXQ,etal.ComputationallyEfficientDOATrackingAlgorithminMonostaticMIMORadarwithAutomaticAssociation[C]∥InternationalJournalofAntennasandPropagation, 2014：1-10.

[12]HAYKINS.AdaptiveFilterTheory[M]. 4thed.EnglewoodCliffs.NJ:Prentice-Hall,2000.

[13]胡莉, 张力伟, 周希元. 基于可变遗忘因子RLS的盲多用户检测[J]. 网络安全与应用技术, 2012(9): 14-17.

HULi,ZHANGLi-wei,ZHOUXi-yuan.BlindMultiuserDetectorBasedonVariableForgettingFactorRLS[J].NetworkSecurityTechnologies&Application, 2012(9): 14-17.

[14]张娟, 张林让, 张楠, 等．一种有效的MIMO雷达相干信源波达方向估计方法[J]. 电子学报, 2011, 39(3): 680-684.

ZHANGJuan,ZHANGLin-rang,ZHANGNan,etal.AnEfficientDOAEstimationAlgorithmofCoherentSourcesforMIMORadar[J].ActaElectronicaSinica, 2011, 39(3):680-684.

[15]符渭波, 苏涛, 赵勇波, 等．空间色噪声环境下基于时空结构的双基地MIMO雷达角度和多普勒频率联合估计方法[J]. 电子与信息学报, 2011, 33(7): 1649-1654.

FUWei-bo,SUTao,ZHAOYong-bo,etal.JiontEstimationofAngleandDopplerFrequencyforBistaticMIMORadarinSpatialColoredNoiseBasedonTemporal-SpatialStructure[J].JournalofElectronic&InformationTechnology, 2011, 33(7):1649-1654.

Target Angle Tracking Algorithm Based on the Covariance MatrixforBistaticMIMORadar

ZHANG Zheng-yan1，ZHOU Qing-song1，HUANG Zhong-rui1，XU Xu-yu2

(1.Electronic Engineering Institute,Anhui Hefei 230037, China；2.PLA，No73677Troop,JingsuNanjing210016China)

Abstract:A new algorithm based on variable forgetting factor is put forward for MIMO radar tracking problem among the target whose speed is changing. Firstly, how the forgetting factor impacts the algorithm convergence speed and estimated performance is analyzed. Secondly, the forgetting factor recursive formula is put forward by referring the variable step size least mean square (LMS) algorithm. Lastly the tracking problem under the variable speed target is solved by brought the forgetting factor recursive formula into PASTd algorithm. Simulation results verify that the convergence speed and performance of the algorithm are greatly improved and the algorithm robustness is enhanced.

Key words:bistatic MIMO radar；variable speed target；angle tracking ；variable forgetting factor；ESPRT；PASTd

*收稿日期：2015-05-05；修回日期：2016-01-10

作者简介：张正言(1991-)，男，安徽宿州人。博士生，主要研究方向为MIMO雷达信号处理，阵列信号处理。

通信地址：230037安徽省合肥市黄山路460号，雷抗系502教研室E-mail：981890451@qq.com

doi:10.3969/j.issn.1009-086x.2016.03.022

中图分类号：TN953+.5；TP301.6

文献标志码：A

文章编号：1009-086X(2016)-03-0134-07