机动式地基无线电导航系统布站策略分析*

杨冬，宋才水

(北京电子工程总体研究所，北京　100854)



机动式地基无线电导航系统布站策略分析*

杨冬，宋才水

(北京电子工程总体研究所，北京100854)

摘要：利用多站测距定位方法实现无线电导航在近年来得到了快速发展。定位精度受到目标和地面机动测量站的几何构型制约。针对基于倒GPS原理的机动式地基导航系统的布站策略问题，建立满足最优解的几何规则布站方式。利用计算机仿真分析典型高度空域的定位精度分布，对我国机动式地基无线电导航系统的布站策略具有指导意义。

关键词：多站测距定位；地基导航系统；定位精度因子；布站策略；最优解；定位精度

0引言

无线电导航技术为各种航空、航天飞行器的飞行提供测控和导航支持, 是空天技术发展中不可或缺的重要组成部分[1]。

目前使用的无线电导航系统，大多使用了多站测距定位方法，即在获得目标接收点与多测量站间的距离后，结合已知的测量站位置从而解算出待定位的目标接收点位置。除了时钟误差、测距误差和传播误差以外，测量站与目标间的几何分布对目标定位精度有较大影响。对于空中导航系统，如GPS卫星导航，测量站的分布问题转化为最优星座选择问题；对于地基导航系统，测量站预先布置在地面上，且数目有限，布站策略对系统的影响较大，因此，有必要研究地基导航系统多测量站的分布策略。

相比于卫星定位系统，陆基导航系统成本低廉，维护保养方便，保密性好，抗干扰能力强，所以已成为一种重要的飞行器导航方式。本文的研究正是基于一种倒GPS原理的地基无线电导航系统，它由数辆能够发射导航信号到地球同步轨道的车载地面站和导航接收机组成，通过通信网构成一个综合体，实现了对高轨航天飞行器的测控和导航支持，目前，该系统已在工程实际中得到应用，其覆盖地球同步轨道能力显著优于陆基导航系统和GPS卫星导航系统，相比统一测控系统，在机动灵活性、适应多目标和多任务方面有一定优势。

三维空间定位精度因子普遍用于各种无线电导航系统的评价，本文从其基本定义出发[2]，建立满足最优解的几何规则布站方式，目的是获得较好的精度因子值，提高系统定位精度。

1导航定位体制

1.1双曲定位

双曲定位体制(n≥4)将测量坐标系建立在站1(主站)，测量站1与其余站返回信号的时间差，就可以获得距离差，利用多普勒频率可以获得距离差的变化率。GPS系统就是这种工作体制的代表[3]，如果将其中一颗星理解成主站，相当于获得的是与其他星间的距离差和多普勒差量。

(1)

速度测量则根据伪多普勒频率测量计算得到的。

该体制的工程设计核心是，每个测量站有一台发射机、一台原子钟和一个卫星双向对时子系统。有一主站统管整个系统，所有其他测量站的原子钟定期与主站进行时间同步。由卫星双向对时子系统保证原子钟之间精确的时间同步。

1.2球定位

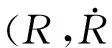
(2)

对于速度量，可以在位置量的求解基础上，由3个站测量多普勒频率求得，测量精度较高。

配合球定位体制工作的应答机必须按频分或时分方式多路应答，因此多路应答机是工程设计的关键问题之一[4]。

2PDOP的定义及表达式

可以通过数学方法证明[2]，在无线电定位导航解算中，采用数学递推的方法,导航定位精度与伪距测量精度之间的关系为

(3)

式中：A为目标与测量站站址相对位置关系的方向余弦矩阵；σ0为等效测距误差。

对于4站双曲定位系统，测量站坐标为(xi,yi,zi),i=1,2,3,4，目标坐标为(x,y,z)，根据伪距测量公式，目标到站1，2，3，4的距离为Ri。其方向余弦矩阵可以表述为

(4)

若时间延时可以通过上下行非相干精确测量，则其对测距几乎没有影响，系统变为3站球定位系统，方向余弦矩阵为

(5)

无论对于3站球定位，还是4站双曲定位，构成距离测量的误差主项相同,因此2种体制的测距精度是基本相同的。在已知飞行轨迹和站点布置的情况下，将式(4)或式(5)代入式(3)中，可以较方便地计算出相应在飞行轨迹每一点上的PDOP值，即表征该点的定位精确性。文献[5]中已得出结论，如果接收机的时间延时可以精确测量，则3站球定位算法的PDOP值要小于4站双曲定位算法。下面主要针对3站球定位算法进行几何建模。

3几何模型

建立一个以目标为原点的坐标系，如图1所示。其中，e1,e2,e3分别表示由目标到3个测量站的单位矢量，ei的方向余弦为exi,eyi,ezi，若使e1和x轴向保持一致，并且e2在Oxy平面内，e2≥0，在此情况下，有

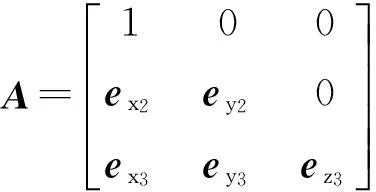
ex2+ey2=ex3+ey3+ez3=1.

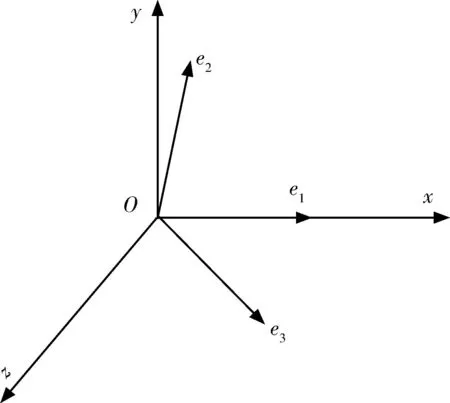
图1　几何模型图Fig.1　Geometry model

由

得到

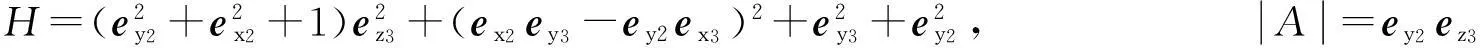
令

ez3-1).

利用拉格朗日待定系数的函数求PDOP的最小值，即F对各参数依次求导，并令其为0。可计算得到：

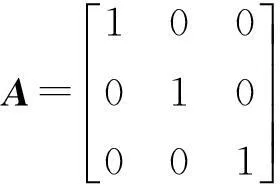
此时，e1,e2,e3任意两者之间的夹角都相等且等于90°，PDOPmin=1.732。即最小误差条件为“三球面正交”。

最优布站策略：

(1) 近距离测量时，选择合适的基线长度和布站形式使得目标和各测量站间矢量的夹角满足正交条件(综合考虑地球曲率对目标观测能力的影响)；

(2) 远距离测量时，尤其是针对地球同步轨道的导航应用，由于实际应用条件的限制，站间距配置无法满足正交条件，应尽可能保证长基线，基线愈长，定位精度愈高。

4系统布站分析

近年来，关于多站测距定位方法系统的最优布站问题研究很多[6-11]，这些文献主要分析了诸如Y型布站[6]、倒Y型布站等多种规则布站形式下定位精度的分布情况。在规则布站条件下,定位精度分布也是规则的，但在不同方向上精度不一致。在实际条件下，由于地形的影响，尤其是作战要求的限制，系统布站并不能保证规则性[7]，站与站之间的基线长度难以保持一致、构形难以对称。文献[9]中研究了不规则布站条件下的定位精度分布,指出基线长度和基线指向改变对定位精度分布的影响。

综合以上分析，系统体制和布站选择结合以下几项：

(1) 球定位体制精度高；

(2) 球体制要求的最少站数是3站，倒三角形布站是典型的无源雷达布站方式之一，与其他典型的布站方式相比较，其局部定位精度较高[11]；

(3) 考虑到若提供比最小定位要求的站数更多的站数，可确保某一站失效时系统的可工作性，在3站基础上增加1个测量站起到对原3个测量站的冗余备份作用，将其置于倒三角形的中心，使构成“倒Y型”[12]；

(4) 对于规则的倒Y型布站，在中心主站-辅站的基线方向上定位精度较高,其反向延长线上的定位精度要稍差；

(5) 基线长度应尽可能满足最优布站策略要求[13]。

5仿真分析

针对高轨航天飞行器导航应用的地基无线电导航系统的布站基线长度受限于我国地域范围，因此，特以目前国土范围所能达到的基线长度进行布站，对系统的工作区域和不同高度空域的定位精度的分布进行仿真分析，如图2所示。

5.1仿真条件

我国最大国土范围：西部(站1)、北部(站2)、南部(站3)，分别部署一测量站，根据相对形状，再选择中西部地区增加一站部署(站4)。

典型高度平面：5 000，10 000，20 000，30 000 km。采用Matlab进行仿真分析，得到不同高度平面下的工作区域及PDOP分布图,如图3所示。

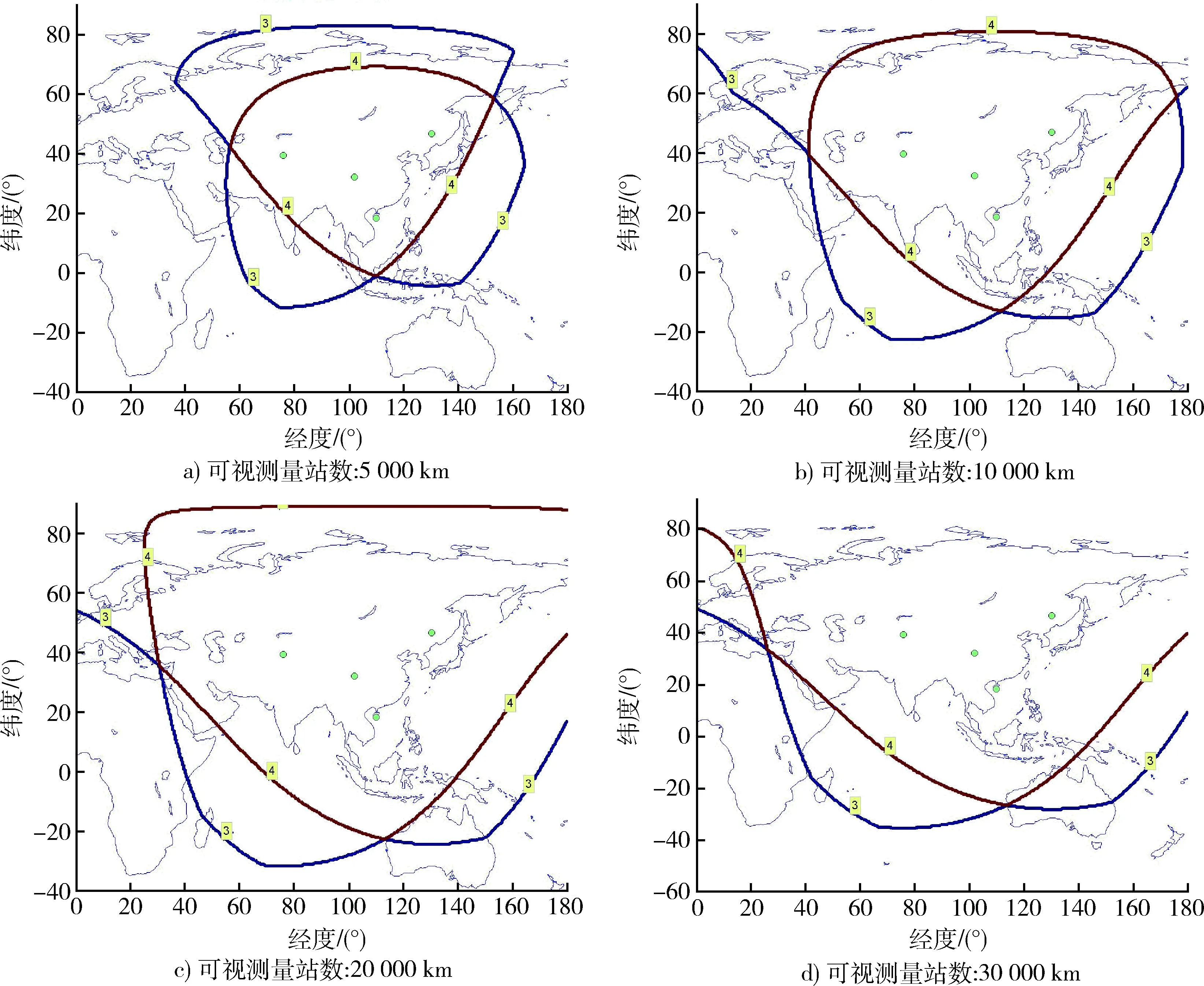
图2　工作区域仿真图Fig.2　Simulation results of working area

5.2工作区域

球定位体制要求的最少3站定位，图中给出了3站与4站同时可视时的系统工作区域。可看出，随着高度的增加，系统工作区域增大，可延伸到南半球。

5.3PDOP分布

结合系统工作区域可看出，随着作用高度的增加，系统精度逐渐降低。在30 000 km高度时，4站工作区域中，PDOP<30；3站工作区域中，PDOP<100。

为了更充分的分析某一站失效时系统的可工作性，固定10 000 km高度平面，分别将以上4个测量站剔除进行仿真，得到PDOP分布图，如图4所示。

由仿真结果可看出：

(1) 倒Y型的中心站对系统工作区域和精度几乎无影响，起到的是冗余备份作用；

(2) 倒Y型的某一分支失效时，对本站头顶空域的精度影响最大[14-15]，且当剩余三站的几何形状恶化到一定程度时，可能会使该站头顶区域PDOP值产生发散趋势，不可定位。

图3　PDOP分布仿真图Fig.3　Simulation results of PDOP map

图4　某一站失效时PDOP分布仿真图Fig.4　New simulation results of PDOP map

6结束语

针对基于倒GPS原理的机动式地基无线电导航系统的布站策略问题，从三维空间定位精度因子的基本定义出发，建立几何模型，得到“三球面正交”的最优布站策略。针对目前我国国土范围内最大布站方式，得到典型高度平面的系统工作区域和定位精度分布，对于我国机动式地基无线电导航系统的布站策略都具有指导意义。

参考文献：

[1]郑焕敏. 把握空天防御发展趋势加快总体部的发展速度[J]. 航天工业管理，2007(2):26.

ZHENG Huan-min. Holding Developing Trend of Space Defending and Accelerating Developing Speed of Design Department[J]. Aerospace Industry Management, 2007(2):26.

[2]庄奇祥，菅曙光，樊能娥. 三维位置几何因子探讨[J].天文学报, 1991, 32(2):113-120.

ZHUANG Qi-xiang, JIAN Shu-guang, FAN Neng-e. An Investigation of the Three Dimensional Position Dilution of Precision[J]. Acta Astronomica Sinica, 1991,32(2):113-120.

[3]Elliott D Kaplan, Christopher J Hegarty. Understanding GPS Principles and Applications[M].2nd ed. Beijing: Publishing House of Electronics Industry, 2008.

[4]刘楠，姜弢，杨莘元. 实现高精度新型陆基无线电导航系统技术难题分析[J]. 弹箭与制导学报,2006,26(2):370-373.

LIU Nan, JIANG Tao, YANG Shen-yuan. Difficult Problems for the New Type Onshore Radio Navegation System of High-Accuracy[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006,26(2):370-373.

[5]王丹丹，王小军. 陆基导航三站定位与四站定位PDOP值分析[J]. 航天控制，2009, 27(5):15-19.

WANG Dan-dan, WANG Xiao-jun. Analysis of PDOP Value of Position by Three Stations or by Four Stations of Ground Based Navigation[J]. Aerospace Control, 2009, 27(5):15-19.

[6]高虎，俞志强. 基于四站时差定位原理的星型布站分析[J]. 空军雷达学院学报, 2004,18(3)：22-24.

GAO Hu，YU Zhi-qiang. Analysis of Star-Model Station Positioning Based on 4-Station TDOA[J]. Journal of Air Force Radar Academy, 2004, 18(3):22-24.

[7]王成，李少洪，黄槐. 测时差定位系统定位精度分析与最优布站[J]. 火控雷达技术,2003,32(1):1-6,30.

WANG Cheng, LI Shao-hong, HUANG Huai. Location Accuracy Analysis and Optimal Distribution of TOA Difference Location System[J]. Fire Control Radar Technology, 2003，32(1):1-6,30.

[8]卫国，张挥.空间目标定位多站布局的若干考虑[J]. 天文学报, 1989, 30(4):401-408.

WEI Guo, ZHANG Hui. Considerations of Stations Distribution For Space Positioning[J]. Acta Astronomica Sinica, 1989, 30(4):401-408.

[9]王瀚，钟丹星，周一宇. 不规则布站时差定位系统定位精度分析[J]. 现代电子技术，2007(7):19-24.

WANG Han, ZHONG Dan-xing, ZHOU Yi-yu. Location Precision Analysis in the Time Difference of Arrival Location System Using Irregular Distribution[J]. Modern Electronic Technique, 2007(7):19-24.

[10]李锐，王雪梅. 陆基导航系统最优布站方法研究[J]. 微计算机信息,2009,25(7-1):194-195.

LI Rui, WANG Xue-mei. Research on Base Station Location for the Land-Based Navigation System[J]. Micro-Computer Information, 2009,25(7-1) :194-195.

[11]王永诚，张令坤. 多站时差定位技术研究[J]. 现代雷达, 2003,25(2):1-4.

WANG Yong-cheng, ZHANG Ling-kun. Position Location Using TDOA Measurements in Multisites[J]. Modern Radar, 2003,25(2):1-4.

[12]邵良琪，邵定蓉. 一种区域定位系统的布站策略[J]. 电子与信息学报，2009,29(3):553-556.

SHAO Liang-qi, SHAO Ding-rong. The Station Arrangement Strategy of a Regional Positioning System[J]. Journal of Electronics & Information Technology, 2009,29(3):553-556.

[13]王贵生，王东进，陈卫东. 基于距离差法目标定位的多站雷达优化布局[J]. 现代防御技术, 2006,34(6):93-97.

WANG Gui-sheng, WANG Dong-jin, CHEN Wei-dong. Multiradar System Optimal Constellation for Target Locating Based on the Method of TDOA[J]. Modern Defence Technology, 2006,34(6):93-97.

[14]常青，柳重堪，张其善. GPS的几何精度因子和定位解的递推算法[J]. 通信学报, 1998,19(12):83-88.

CHANG Qing, LIU Zhong-kan, ZHANG Qi-shan. The Recurrence Algorithm for GDOP and Positioning Solution in GPS[J]. Journal of China Institute of Communications, 1998,19(12):83-88.

[15]帅平，曲广吉. 卫星导航定位方程的病态条件[J]. 飞行器测控学报,2006,25(1):1-5.

SHUAI Ping, QU Guang-ji. Ill Conditions of Satellite Navigation Positioning Equations[J]. Journal of Spacecraft TT&C Technology, 2006,25(1):1-5.

Deployment Strategy Analysis of Motorized Ground-Based Navigation System

YANG Dong, SONG Cai-shui

(Beijing Institute of Electronic System Engineering, Beijing 100854, China)

Abstract:The navigation method using multi station location has achieved rapid development in recent years. Accuracy is restricted by the geometric configuration between the target and the station. Aiming at the stations distribution strategy of the motorized ground-based navigation system, the geometric model of the optimal solution is established. PDOP value of position distribution map of typical height is simulated, which is of the guiding significance for the distribution strategy.

Key words:multiple-station range finding positioning; ground-based navigation system; positioning accuracy factor; stations distribution strategy; optimal solution; positioning-accuracy

*收稿日期：2015-07-21；修回日期：2015-08-17

基金项目：有

作者简介：杨冬(1986-)，女，河南新乡人。硕士，工程师，研究方向为无线电导航技术、探测制导。

通信地址：100854北京市142信箱30分箱E-mail：331652485@qq.com

doi:10.3969/j.issn.1009-086x.2016.03.005

中图分类号：TN953;TP391.9

文献标志码：A

文章编号：1009-086X(2016)-03-0025-07

导航、制导与控制