红外点目标跟踪方法综述*

关键词：红外点目标；检测；跟踪；先跟踪后检测；贝叶斯估计；多目标

0引言

传统意义上，在点目标跟踪过程中，一般先利用阈值将目标从含噪声的图像中分割出来，再将各帧分割出来的目标关联起来形成轨迹。由于噪声的幅值也可能超过阈值，因此被分割出来的点可能是目标，也可能是虚警，这些点在本文中统称为“潜在目标”。若目标的信噪比高、同时目标数目不多，那么很容易选择合适的阈值将真目标较“干净”地分割出来，且跟踪目标也相对简单。但实际上，常常需要同时跟踪大量的目标，另外也更希望跟踪尽可能远的目标(即信噪比尽可能低的目标)，这使目标的跟踪问题变得相对复杂。若目标的数目很多且分布相对密集，则跟踪的难点在于如何处理潜在目标与轨迹的分配，即后文提到的关联冲突。而若目标的信噪比很低、潜在目标中虚警所占比例大，那么从潜在目标中挑选真目标会变得困难、也容易出错，故跟踪的难点在于如何从大量潜在目标中准确区分少数的真目标。实际的跟踪问题往往是以上两方面的结合，依据侧重点的不同，逐渐形成了不同的目标跟踪方法。

从20世纪六七十年代起，人们开始系统地研究点目标跟踪问题，将常见的目标跟踪算法暂且分为3个研究阶段。早期的研究集中在实现基本的单步目标跟踪，其中全局最近邻(GNN)算法[1]、概率数据关联(PDA)算法[2]及联合概率数据关联(JPDA)算法[3-4]是其中的代表。GNN算法是最基本的跟踪方法，建立了包括目标预报、目标搜索及轨迹关联在内的整个目标跟踪过程。PDA算法首次将加权平均的概念引入目标跟踪过程中，减少了目标轨迹被虚警“拉走”的可能性。JPDA算法则是最早提出利用剔除矛盾假设的办法解决多目标关联冲突的跟踪方法，其“多种可能就做多种假设”的想法为接下来的跟踪算法研究提供了发展思路。

随后的研究逐渐侧重于利用多步策略解决较低信噪比的目标的跟踪问题。在众多研究成果中，多假设跟踪(MHT)算法[5-7]和动态规划算法(DPA)[8]是其中的代表。MHT算法是应用最为广泛的利用多步跟踪和延迟逻辑来确定真目标的方法，它提供了非常优秀的目标跟踪性能。DPA算法是一种重要的先跟踪后检测算法，也是目前最有效的低信噪比目标跟踪方法，它通过逆向分步寻优实现在跟踪过程中检测目标，取得了检测效果和计算量上的平衡。

近年来，研究热点侧重于解决如何快速跟踪大量目标的问题。对这类问题，JPDA，MHT等传统算法都是通过对潜在目标的分配，将多目标联合跟踪问题转变为多个并行的单目标跟踪问题来处理。当目标数多，这种处理办法会导致关联假设过多，关联组合爆炸。Markov链蒙特卡罗(MCMC)数据关联方法[9]，利用有限的样本数对潜在目标的最优分配进行估计，被证明有效减小了算法在多目标跟踪时的计算量。而基于有限集统计(FISST)理论的概率假设密度(PHD)滤波方法[10]，利用PHD实现了多目标的联合跟踪，避免了对潜在目标的分配，也就减小了跟踪目标的计算量，改善了跟踪性能。PHD方法被普遍认为是目前最有发展前景的多目标跟踪方法。

1目标跟踪方法

1.1搜索区域的设置

引言提到，受噪声影响，潜在目标中存在虚警。在利用已有目标轨迹预测出下一时刻的目标位置后，若以预测位置为中心设置搜索范围，在该区域中寻找目标，则可大幅度降低虚警与目标轨迹匹配的可能性，提高目标的跟踪性能。

区域的大小要考虑虚警和漏检2方面的因素。区域太大则虚警增加，太小则漏检增加。Sea先后提出了矩形和椭圆区域的设置方法，其中的椭圆区域得到了广泛的应用，其半径的确定方法如下[1]。

首先定义对数似然比函数

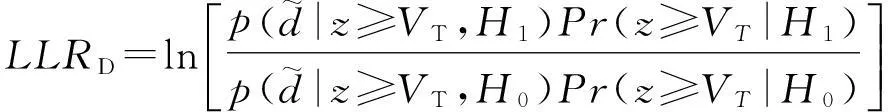
(1)

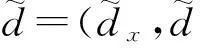
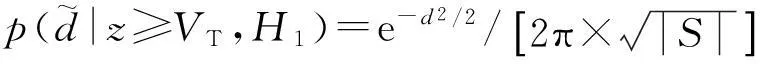
(2)

(3)

这样，式(1)可以化成

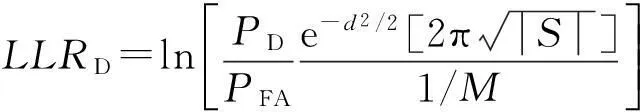
(4)

定义另外一个对数似然比函数LLRU，

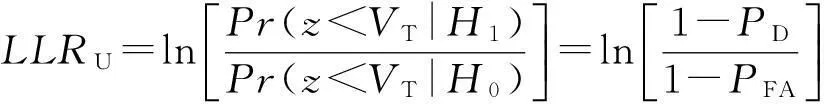
(5)

由于PFA通常很小，则LLRU可简化为

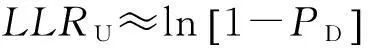
(6)

为使目标能够被分割出来，要求LLRD大于或等于LLRU，即

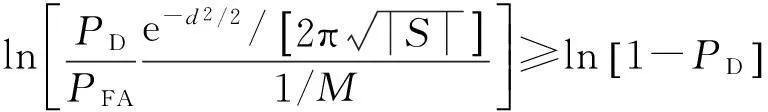
(7)

则

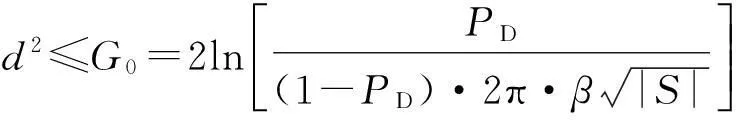
(8)

式中：

β=PFA/M，

(9)

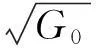
1.2全局最近邻(GNN)算法

GNN算法[1]是最基本的跟踪方法，其实现方式如下。

在搜索区域内，将潜在目标j与真目标i的相似程度用似然函数gij表示：

(10)

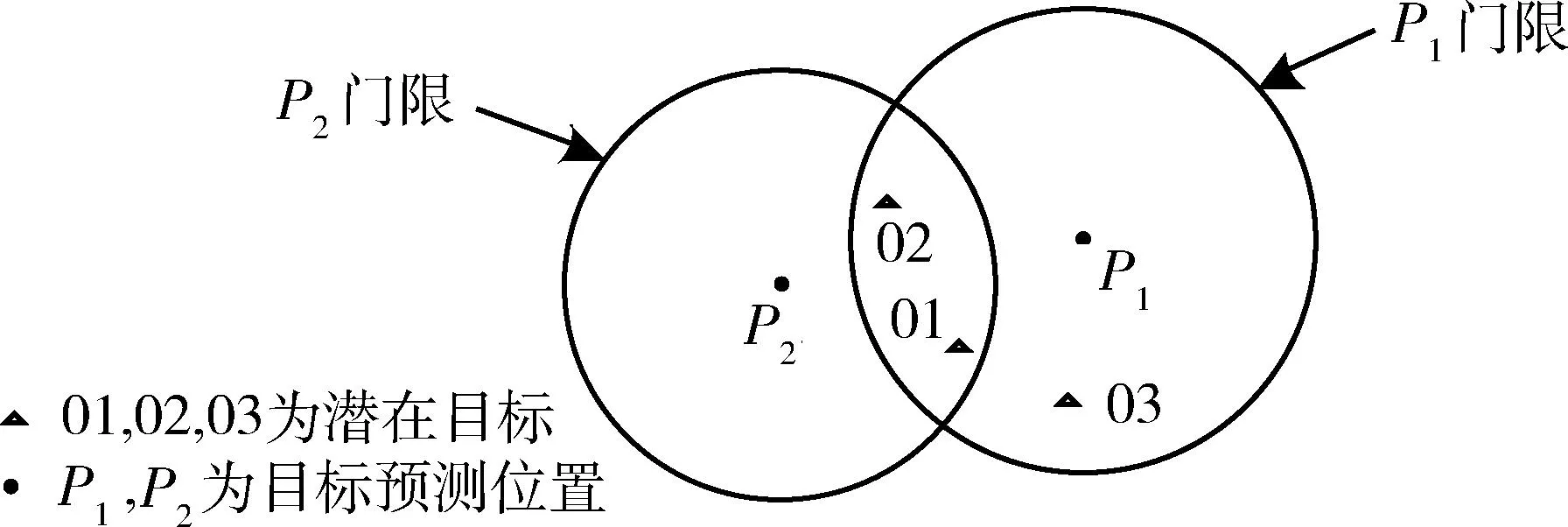
图1　关联冲突情况示例Fig.1　Illustration of association conflict

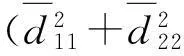
表1　关联冲突的分配矩阵

若分配矩阵较大，计算量会很大。对这一分配问题，Kuhn最初利用Hungarian算法[12]寻找最优解，但该算法只能求解正方形的分配阵。为此，Munkres等人提出了可求解一般矩形分配阵的Munkres算法[13-14]。随后，Jonker和Bertsekas等人提出了J-V松弛算法[15]和拍卖算法[16]，进一步减小了分配耗时。

显而易见，若目标的信噪比很高、搜索区域内不含虚警，GNN算法的目标轨迹就是真目标轨迹。但由于该方法将目标预测位置附近的某个单点作为真目标，则一旦区域内存在虚警，目标轨迹就可能被“拉走”，使接下来的目标预测精度下降，从而可能导致连续地选择假目标进行轨迹关联，甚至导致轨迹中断。故只要搜索区域内存在虚警，算法的跟踪性能就会明显下降。

1.3概率数据关联(PDA)算法

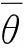
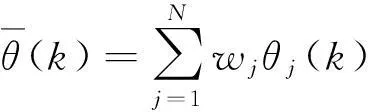
(11)

式中：权值wj为

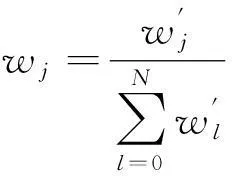
(12)

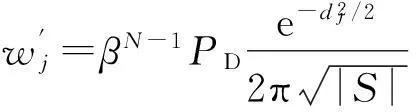
(13)

这样，用潜在目标的加权代替由GNN算法选出的单个潜在目标，PDA算法能够减小目标轨迹被虚警“拉走”的机会。仿真结果显示，采用PDA算法可以显著减小门限内偶尔存在虚警时，目标跟踪丢失的概率[2]。

应该指出，采用PDA算法给目标跟踪带来的改善是有限的。若某一帧门限内虚警较多、或接连几帧门限内均存在虚警，目标轨迹仍会被“拉走”，致使跟踪性能下降。同时，由于PDA算法的目标轨迹均由加权目标构成，只要存在虚警，其轨迹与真目标轨迹之间就存在偏差。而相同条件下，GNN算法的轨迹若未被假目标拉走，其轨迹与真目标轨迹是相同的。

1.4联合概率数据关联(JPDA)算法

为解决PDA算法在多目标跟踪时的关联冲突，Bar-Shalom等人在PDA算法的基础上又提出了JPDA算法[3-4]。仍以图1的情况为例，JPDA算法先列出所有的轨迹关联假设，再将其中存在关联冲突的假设去掉，计算剩余的各关联假设hi的概率p(hi)，见表2。以h2为例，p(h2)相当于事件“P1与01关联”及事件“P2轨迹中断”同时发生的概率。因为01为P1的目标的概率是PDg11，02，03是虚警的概率是β2，P2的目标没被分割出来的概率是(1-PD)，故

p(h2)=β2PD(1-PD)g11.

(14)

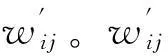
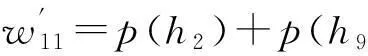
(15)

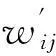
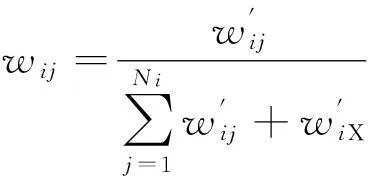
(16)

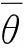
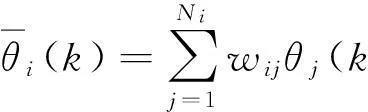
).　(17)

对JPDA算法来说，若想计算式(13)中的wij，必须列举出全部的关联假设。如果目标的个数多，那么关联假设的数量就会很多，出现NP-hard问题[17-20]，导致JPDA算法的计算量很大。为此，Oh等人提出了一种Markov链蒙特卡罗数据关联(MCMCDA)算法[9]。该算法对表2的部分关联假设采样，再利用Markov链蒙特卡罗方法由样本来估计wij。这样，计算wij前无需再将全部假设列举出来，仅需有限的关联假设样本就可以了。仿真结果表明，在跟踪大量目标时，MCMCDA算法比JPDA算法更有效率，而跟踪性能相差不大。

上述方法只适用于信噪比高的目标。如果目标的信噪比低，受虚警的影响，这些方法就很难达到要求的跟踪性能。为实现对低信噪比目标的有效跟踪，常采用多步跟踪和延迟逻辑，将多帧数据结合在一起使用，以达到或增强目标的信噪比、或更好的区分目标与虚警的目的。

1.5多假设跟踪(MHT)算法

单步跟踪算法之所以不适用于低信噪比目标，是因为只通过单帧图像很难区别目标和虚警。由于目标在图像中的运动是有规律的，若观察连续多帧图像中潜在目标的位置的规律，则不难将真目标甄别出来。多步跟踪方法就是由这种思想发展而来。

Reid提出的MHT算法是一种典型的多步跟踪算法[5-7,21]。还以图1为例，k时刻各轨迹与潜在目标的单步关联有10种假设。在下一时刻，若在各轨迹的搜索区域内仍存在多个潜在目标，每一个关联假设又会派生出多个新的关联假设，例如图2中由h6派生出的h6,1和h6,2等。考虑k时刻某单步关联假设hi及与其相关的所有历史假设的集合，若将评价函数s(k)定义为该集合中各关联假设的概率pk(hi)之和，即

s(k)=s(k-1)+pk(hi)，

(18)

利用SPRT[22]等方法对上述评价函数进行假设检验，即可得到真目标轨迹。

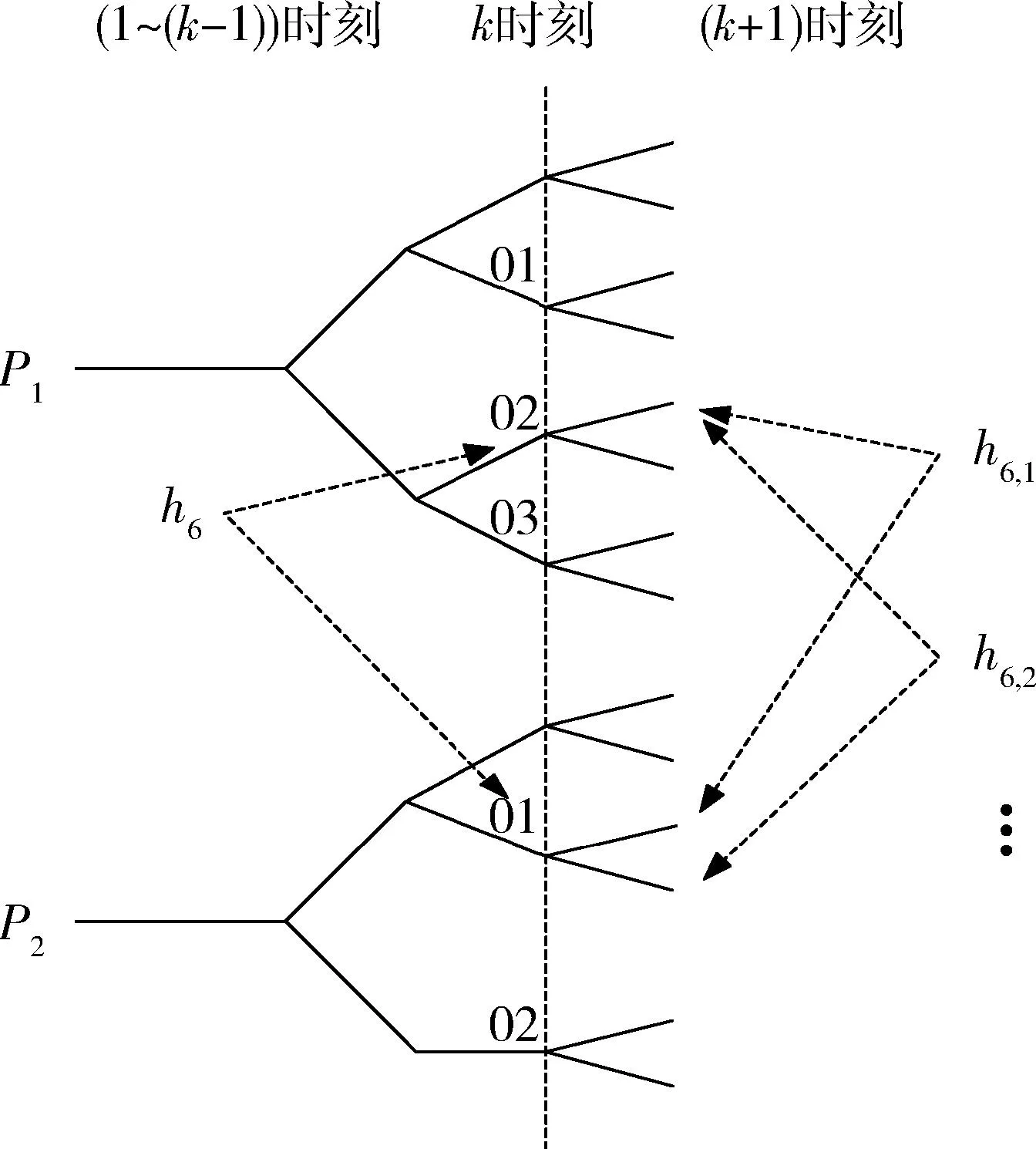
图2　MHT假设示意图Fig.2　Hypothesis for MHT

关联假设的数量由待跟踪目标个数及各搜索区域中潜在目标数决定，每增加一步跟踪，算法的计算量就会以指数增长。在虚警较多时，若不限制假设的规模，很容易出现组合爆炸。在实际使用中，MHT算法需不断地剔除分数低的假设以减小计算量。Murty算法[23-26]，Deb和Popp等人提出的s-d分配算法[27-28]以及Kurien等人提出的面向轨迹的MHT[29-31]等均是有效的假设剔除算法。Blackman等人指出，MHT算法在剔除错误假设后是有可能做到实时计算的[32-33]。同时，de Feo等人在比较多种跟踪方法后指出，若不考虑计算量，MHT算法具有在高虚警环境下跟踪目标的明显优势[34-35]。

在低信噪比情况下，需要降低图像分割阈值确保跟踪过程中不漏掉目标，但这会提高虚警概率。如对信噪比SNR=2的目标，若要求检测概率PD≥0.98，则虚警概率PFA≈0.52，即每帧由虚警产生的潜在目标数超过图像像素数的一半，关联假设的数量很大。若虚警概率增大到一个极限值，比如PFA=1(即不对图像进行阈值分割)，则MHT算法实际上成为一种对目标轨迹穷举式的搜索。以单目标跟踪为例，设图像由M个像元构成，若假定搜索区域为整幅图像，各时刻目标的位置均有M种可能(即存在M个关联假设)，各关联假设在下一时刻又派生出M个新的关联假设，即n帧后目标轨迹的关联假设数为Mn，致使MHT算法失去了工程实用价值。为此，我们需要一种减小穷举式搜索的计算量、以实现低信噪比目标跟踪的方法，即下文介绍的DPA算法。

1.6动态规划算法(DPA)

DPA算法是一种常见的检测和跟踪低信噪比目标的方法。经由Bellman，Larson，Viterbi等人对DPA的不断完善[36-38]，Barniv首次将其用于低信噪比目标的检测，并对跟踪性能进行了详尽地分析[8,39]。

以跟踪单个目标为例，若将目标轨迹记为(θ(n),θ(n-1),…,θ(1))，则对目标的估计可由评价函数s(θ(n),θ(n-1),…,θ(1))的n维寻优得到，即

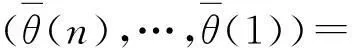
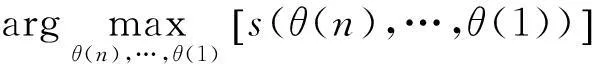
(19)

如前文所述，该n维寻优的计算量很大。若能将s(θ(n),θ(n-1),…,θ(1))拆分成多个相互独立或仅部分相关的子评价函数之和，例如拆成如2个首尾相关的子评价函数

s(θ(n),…,θ(k+1),θ(k),…,θ(1))=

s(θ(n),…,θ(k))+s(θ(k),…,θ(1)).

(20)

则式(19)的寻优过程便可大大简化。但在一般情况下，评价函数均是不能拆分的，例如式(18)就无法写成类似式(20)的形式，这一点借助式(10)，(15)及式(18)很容易证实。

Barniv找到了一种具有上述“可拆分”性质的评价函数[8,39]，他将式(18)的pk(hi)定义为

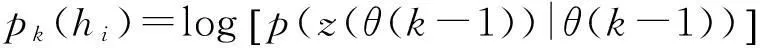
(21)

式中：z为测量值；pk(hi)为θ(k)与θ(k-1)的关联概率。由于按式(21)定义的pk只与pk-1相关，故s(θ(n),θ(n-1),…,θ(1))可拆分成n个只首尾相关的函数之和，即

s(θ(n),θ(n-1),…,θ(1))=

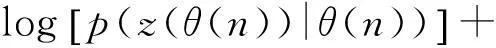
pn(θ(n),θ(n-1))+…+p2(θ(2),θ(1)).

(22)

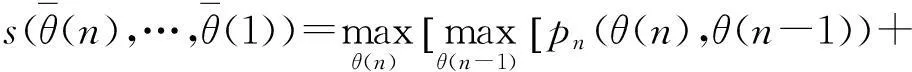
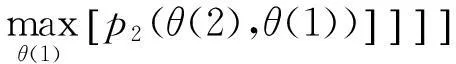
(23)

DPA算法的这种分步寻优，使算法的计算量由Mn减小为M2n，令其在检测低信噪比目标时，比MHT算法高效得多。

为进一步减小算法的计算量，可在各时刻k，将θ(k-1)的搜索范围限制在以θ(k)为中心的某个区域内。搜索区域的大小由目标运动的快慢决定：目标运动越快，θ(k-1)离θ(k)就会越远，搜索区域就要越大。

和Barniv的工作类似，Arnold找到了另一种“可拆分”的评价函数，他将pk(hi)定义为[40]

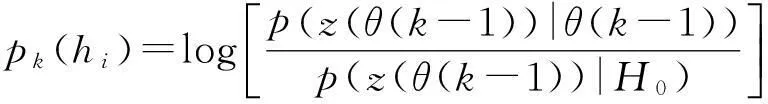
(24)

该评价函数能够比式(21)更有效地区分服从混合高斯分布的目标及噪声,如图3所示。

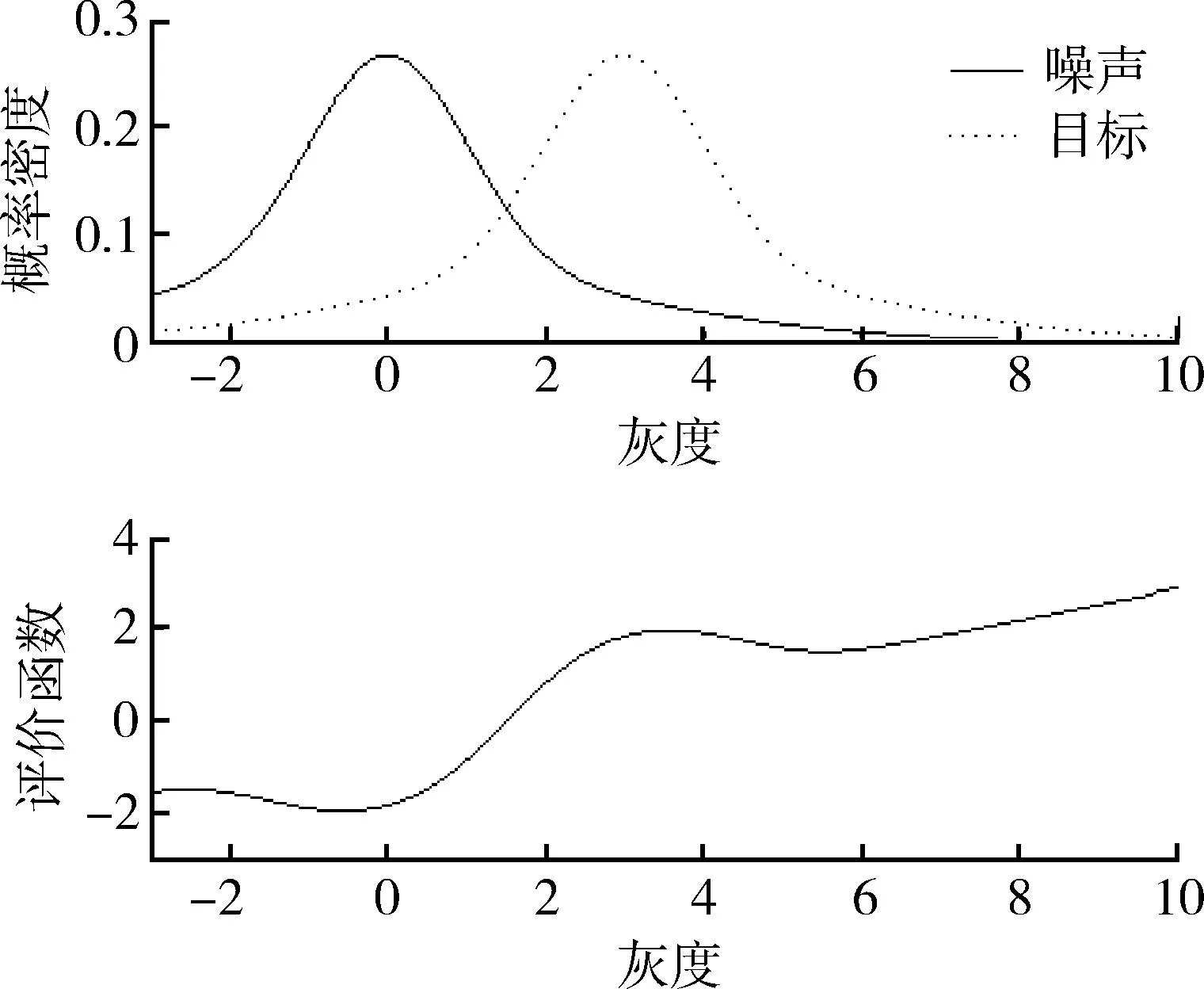
图3　Arnold评价函数特性Fig.3　Merit function for Arnold DPA

由式(21)，(24)，Barniv及Arnold的评价函数均利用了目标及噪声的先验信息。在目标信噪比很低时，先验信息可以帮助我们将目标从噪声中更好地辨别出来。但先验信息又是一把“双刃剑”，即若先验信息不准，如对a(k)的估计与实际存在较大误差，它反而会使检测性能变差。

为此，Tonissen给出了一种不涉及先验信息，而只与测量值z相关的评价函数[41]

pk(hi)=z(θ(k-1)).

(25)

利用Tonissen的评价函数，无论a(k)的估计是否准确，算法的性能均不受影响。但也正是由于缺少先验信息的修正，Tonissen方法对低信噪比目标的检测性能不如Barniv及Arnold方法。

DPA算法存在一些不足。

首先，跟踪算法一般从2个方面综合衡量某潜在目标为真目标的可能性：一是看各潜在目标的幅值，即图像中越“亮”的潜在目标越可能是真目标；二是看各潜在目标与目标预测位置的距离，即与目标预测位置越接近的潜在目标越可能是真目标。由于DPA算法不具备预测目标位置的能力，仅从“亮度”单方面评价寻优结果的好坏，这样目标的信噪比越低，“亮度”这一判断标准越不可靠，致使DPA算法在检测运动目标的过程中，目标运动越快，搜索区域越大，DPA算法受噪声干扰的机会越多，检测性能越弱。

其次，为分辨由式(17)得到的最优轨迹是否为目标轨迹，需对评价函数值进行假设检验。在目前的研究中，目标和噪声轨迹的评价函数均视为服从高斯分布[39,41]，而事实上，评价函数近似服从极值分布[42]。统计特性的偏差会影响对检验门限的估计，进而影响辨别目标轨迹的准确性。

再次，由于目标的评价函数值最大，其周围的噪声会关联到目标轨迹上，且离目标越近，关联越容易产生。噪声与目标轨迹关联会使其评价函数值增大，反映到评价函数图像上则表现为目标周围也被“点亮”，这种现象被称为评价函数的扩散[43]，如图4所示，其中A，B，C为目标。由于评价函数的扩散，某目标可能被其他目标的扩散区域覆盖，导致它在评价函数中无法“解析”(例如图中目标B，C的情况)，给多目标的跟踪带来困难[44]。

事实上，扩散等同于图1的关联冲突。对这一问题，JPDA和MHT两算法采用从所有的关联假设中，剔除关联冲突假设的解决办法。与之类似，Pulford等人提出了下述多假设Viterbi数据关联(MH-VDA)算法[45]。

图4　评价函数的扩散Fig.4　Scattering of merit function for DPA

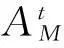
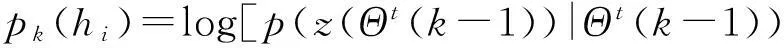
(26)

若k时刻各目标的测量值z(θi(k))相互独立，则

p(z(Θt(k-1))|Θt(k-1))=p(z(θ1(k-1))|θ1(k-1))p(z(θ2(k-1))|θ2(k-1))…

p(z(θt(k-1))|θt(k-1)).

(27)

由式(17)，算法在各时刻k对各Θt(k)寻找(k-1)时刻最优的Θt(k-1)，建立各目标轨迹的单步关联，并以此类推得到t个目标的轨迹。

由于在寻优中，Pulford方法始终保持各假设的目标数量一致，因此避免了将多个目标与一个目标关联，也就避免了关联冲突。这样就防止了图4中扩散的产生，使算法能够准确将多个目标检测出来。

显然，Pulford方法要做的假设会更多，远多于MHT算法。事实上，假设的数量为

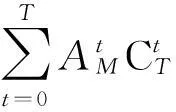
其中：C为组合数。

在此小结一下上述目标跟踪方法。实际上，它们都基于贝叶斯估计。对单目标情况，先利用Bayes预测和更新方程计算各时刻潜在目标θ(k)的后验密度，即

p(θ(k)|zk-1)=∫p(θ(k)|θ(k-1))p(θ(k-1)|

zk-1)dθ(k-1)，

(28)

p(θ(k)|zk)=K-1p(zk|θ(k))p(θ(k)|zk-1)，

(29)

式中：K-1为归一化系数；p(θ(k)|θ(k-1))为目标的状态转移概率。

式(28)对应1.1节一开始所提到的由已有目标轨迹预测接下来的目标位置的过程。式(29)则实现了利用新的测量zk来修正预测结果，p(θ(k)|zk)对应为式(10)潜在目标θ(k)的似然函数gij。

随后，利用上述后验密度来估计真目标位置。常用的估计方法包括极大后验估计(MAP)和期望后验估计(EAP)。对极大后验估计，真目标被视为后验密度最大的那个潜在目标，即

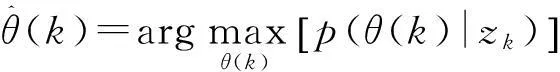
(30)

也就是GNN。对期望后验估计，真目标位置为各潜在目标位置以各自的后验密度为权值的加权平均，即

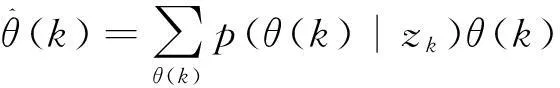
(31)

也就是PDA。而对MHT，DPA等多步方法，评价函数s(·)相当于目标轨迹上各状态的后验密度之和，由于真目标被视为评价函数最大者，故它们同样基于极大后验估计。

对多目标情况，式(28)，(29)中的单目标后验密度p(θ(k)|zk)及状态转移概率p(θ(k+1)|θ(k))变为多目标后验密度p(Θ(k)|zk)及状态转移概率p(Θ(k+1)|Θ(k))。由此，后验密度的预测和更新方程相应变为

p(Θ(k+1)|zk)=

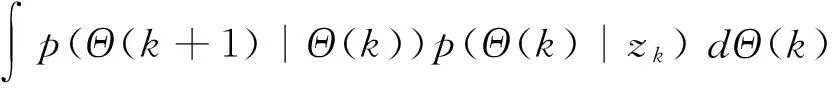
(32)

p(Θ(k+1)|zk+1)=K-1p(zk+1|Θ(k+1))·

p(Θ(k+1)|zk).

(33)

数学上，由于后验密度p(Θ(k)|zk)是高维的，式(32)，(33)很难直接计算。为此，一般假设各目标的状态及观测相独立，这样p(Θ(k)|zk)就可近似为各目标i(i=1,…,T)的后验密度p(θi(k)|zk)的乘积，即

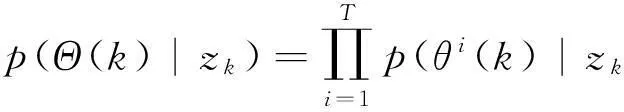
(34)

从而实现了对p(Θ(k)|zk)的降维计算，将多目标跟踪问题转化为多个相独立的单目标跟踪问题，简化了计算难度。为满足式(34)的假设，需在每一步跟踪目标之前剔除轨迹与潜在目标的关联冲突(如图1所示)，这也就是JPDA，MHT等方法在跟踪多目标时需要列出表2的原因。

然而，式(32)的假设经常是不成立的。比如，若目标重合，在重合处就存在着关联冲突。所以，若想从根本上解决多目标跟踪问题，必须要找到直接或者近似计算多目标后验密度p(Θ(k)|zk)的方法。

近年来，Mahler借助有限集统计理论(FISST)，提出用概率假设密度(PHD)来近似p(Θ(k)|zk)，并在此基础上提出了PHD滤波方法，解决了近似计算多目标后验密度的问题[10,46]。

1.7概率假设密度(PHD)滤波方法

Mahler将高维的后验密度p(Θ(k)|zk)用一个二维的“假设密度”PHD近似，实现了对p(Θ(k)|zk)的降维计算。

二维平面上某状态θ(k)的PHD(记为D(θ(k)))被定义为各目标i在θ(k)处的后验密度p(θi(k)|zk)之和。这样，PHD就有了明确的物理意义，即θ(k)的PHD越大，该θ(k)就越可能是目标，且某区域内各θ(k)的PHD的积分即为该区域内目标数的期望。

在此基础上，Mahler用对PHD的预测和更新来近似式(32),(33)的对p(Θ(k)|zk)的预测和更新，即

(35)

式中：λ为与虚警有关的常数。

由于式(35)仅计算各状态θ(k)处的后验密度，并不用来估计目标位置和它的轨迹，所以在得到二维平面上各θ(k)的PHD之后，需采用类似极大后验估计或者期望后验估计方法，由后验密度估计目标位置并形成轨迹[47-52]。

Erdinc等人指出，若目标漏检，PHD的计算会出错[53-54]。为此，Mahler引入目标数的高阶项提出了势概率假设密度(CPHD)滤波方法[54-56]。此外，Vo、Melzi等人提出了序贯蒙特卡罗PHD滤波、Gauss混合PHD滤波、快速傅里叶变换PHD滤波等快速计算PHD的方法[57-60]。其他有关PHD方法的发展及应用请参见文献[61]。

相比JPDA、MHT等传统算法，PHD避免了在跟踪多目标时剔除关联冲突、列举关联假设hi，这样就减小了计算量，防止了在目标数目多时遇到NP-hard问题。所以，PHD能更好完成对大量目标的跟踪任务。但Punithakumar等人发现，在跟踪低信噪比目标时，利用PHD会产生较大的轨迹偏差[62]，其目标跟踪性能与DPA算法相比还有一定差距。

2各算法的分析比较

前文介绍了一系列基于Bayes估计的目标跟踪算法。依照不同的后验密度估计准则，可以将它们大致分为基于极大后验估计的方法，以及基于期望后验估计(即“加权平均”)的方法2类。基于“加权平均”的方法一般采用单步跟踪，利用平均思想减小因偶尔误关联导致目标丢失的概率。然而，就像前面介绍PDA算法时所提到的，若目标信噪比低、虚警接连出现在目标周围，目标轨迹仍会被虚警“拉走”，导致目标轨迹中断。因此，这类方法在信噪比高的环境中更能发挥优势。

相对而言，基于极大后验估计的跟踪算法，特别是MHT、DPA这种多步算法，其优势体现在低信噪比目标的跟踪上。多步跟踪算法可以利用多帧测量信息，结合目标运动特可更准确地判断低信噪比目标的真正位置。相比MHT，DPA在跟踪性能和计算量上取得了较为理想的平衡，是目前跟踪低信噪比目标的首选。但正如前文所提到，它对运动目标的跟踪性能偏弱、无法准确估计评价函数分布、难以跟踪多个密集目标。

在跟踪多目标方面，认为Pulford等人提出的结合多假设的DPA(即MH-VDA)是目前较好的解决方式。但该方法计算量很大，离工程实现还很遥远。PHD滤波方法采用对多目标联合后验密度的降维估计，克服了其它算法跟踪多目标计算量大的问题。然而，它在轨迹生成、低信噪比目标跟踪等方面还存在不足，进一步研究的空间很大。表3分别从对信噪比的要求、多目标跟踪能力、以及跟踪单目标和多目标的计算量等角度对各算法的优缺点进行了比较。为达到理想的跟踪效果，选择算法时应依据实际需求，从对目标的跟踪要求、工程实现的复杂程度以及计算量等方面综合衡量。

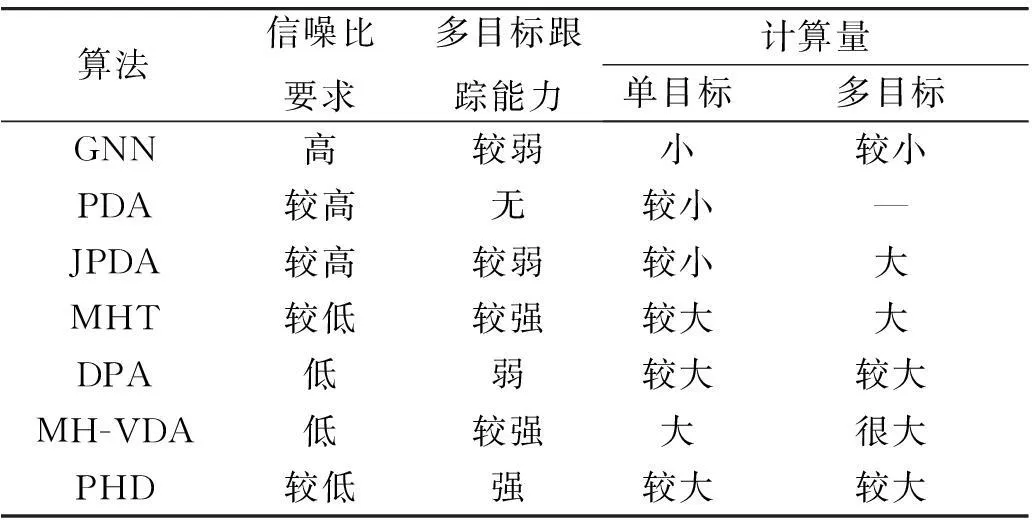
表3　算法的分析比较

3结束语

本文综述了红外点目标的跟踪算法，介绍了算法之间的联系以及各自的特点，并从多个角度对它们加以了分析和对比。目前，多目标跟踪性能较好的算法对低信噪比目标的跟踪性能普遍较弱。反之，对低信噪比目标跟踪性能较好的算法对多目标的跟踪能力或者偏弱，或者计算量很大以致难以应用。本文综述的各算法中，DPA和PHD相对其他算法分别在暗目标和多目标跟踪问题上更具优势。我们认为，对它们的完善和改进将是今后很长一段时间的研究重点。

参考文献：

[1]BLACKMAN S, POPOLI R. Design and Analysis of Modern Tracking Systems[M].Norwood,MA: Artech House, 1999.

[2]BAR-SHALOM Y, KIRUBARAJAN T, LIN X.. Probabilistic Data Association Techniques for Target Tracking with Application to Sonar, Radar and EO Sensors[J]. IEEE Aerospace and Electronic Systems Magazine,2005, 20(8): 37-56.

[3]FORTMANN T.E, THOMAS E, BAR-SHALOM Y, et al. Sonar tracking of Multiple Targets Using Joint Probabilistic Data Association[J]. IEEE Journal of Oceanic Engineering, 1983, 8(3): 173-184.

[4]BAR-SHALOM Y, FORTMANN E T. Tracking and Data Association[M].New York: Academic Press, 1988.

[5]REID D B. An Algorithm for Tracking Multiple Targets[J]. IEEE Trans. on Automatic Control, 1979, 24(6): 843-854.

[6]REID D B. A Multiple Hypothesis Filter for Tracking Multiple Targets in a Cluttered Environment[R]. Lockheed Missiles and Space Company Report No. LMSC, D-560254, 1977.

[7]BLACKMAN S S. Multiple Hypothesis Tracking for Multiple Target Tracking[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 5-18.

[8]BARNIV Y. Dynamic Programming Solution for Detecting Dim Moving Targets[J]. IEEE Trans. on Aerospace and Electronic Systems, 1985, 21(1): 144-156.

[9]OH S, RUSSELL S, SASTRY S. Markov Chain Monte Carlo Data Association for Multi-Target Tracking[J]. IEEE Trans to Automatic Control, 2009, 54(3):481-497.

[10]MAHLER R. Multi-Target Bayes Filtering Via First-Order Multi-Target Moment[J]. IEEE Trans. on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[11]TRUNK G V, WILSON J D. Track Initiation of Occasionally Unresolved Radar Targets[J]. IEEE Trans. on Aerospace and Electronic Systems, 1981, 17(3):122-130.

[12]KUHN H W. The Hungarian Method for The Assignment Problem[R]. Naval Research Logistics Quarterly No. 2, 1955: 83-97.

[13]MUNKRES J. Algorithm for The Assignment and Transportation Problems[J]. J. SIAM, 1957, 5(2): 32-38.

[14]BURGEOIS F, LASSALLE J C. An Extension of the Munkres Algorithm for the assignment Problem to Rectangular Matrices[J]. Communications of the ACM, 1971, 14(1):802-806.

[15]JONKER R, VOLGENANT A. A Shortest Augmenting Path Algorithm for Dense and Sparse Linear Assignment Problems[J]. Computing, 1987, 38(4): 325-340.

[16]BERTSEKAS D P. The Auction Algorithm for Assignment and Other Network Flow Problems: A Tutorial[J]. Interfaces, 1990,20(2): 133-149.

[17]COLLINS J, UHLMANN J. Efficient Gating in Data Association with Multivariate Distributed States[J]. IEEE Trans. on Aerospace and Electronic Systems, 1992, 28(3): 909-916.

[18]OH S. A Distributed Deterministic Approximation Algorithm for Data Association[C]∥IEEE International Conference on Distributed Computing in Sensor Systems and Workshops, 2011.

[19]SCHULZ D, BURGARD W, FOX D, et al. Tracking Multiple Moving Targets with a Mobile Robot Using Particle Filters and Statistical Data Association[C]∥IEEE International Conference on Robotics and Automation, 2001:1665-1670.

[20]NEMETH C, FEARNHEAD P, MIHAYLOVA L. Sequential Monte Carlo Methods for State and Parameter Estimation in Abruptly Changing Environments[J]. IEEE Trans. on Signal Processing, 2014, 62(5): 1245-1255.

[21]BAR-SHALOM Y, BLACKMAN S, FITZGERALD R. The Dimensionless Score Function for Multiple Hypothesis Tracking[C]∥SPIE Signal and Data Processing of Small Targets, Vol. 5913, 2005.

[22]BLOSTEIN S D, HUANG T S. Detecting Small, Moving Objects in Image Sequences Using Sequential Hypothesis Testing[J]. IEEE Trans. on Signal Processing, 1991, 39(7): 1611-1629.

[23]COX I J, HINGORANI S L. An Efficient Implementation of Reid’s Multiple Hypotheses Tracking Algorithm and Its Evaluation for The Purpose of Visual Tracking[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 1996, 18(2): 138-150.

[24]DING Z, VANDERVIES D. A Modified Murty Algorithm for Multiple Hypothesis Tracking[C]∥SPIE Signal and Data Processing of Small Targets, Vol. 6236, 2006.

[25]HE X, THARMARASA R, PELLETIER M, et al. Accurate Murty’s Algorithm for Multitarget Top Hypothesis Extraction[C]∥Proceedings of the 14th International Conference on Information Fusion, 2011.

[26]FORTUNATO E, KREAMER W, MORI S, et al. Generalized Murty’s Algorithm with Application to Multiple Hypothesis Tracking[C]∥10th International Conference on Information Fusion, 2007.

[27]DEB S, YEDDANAPUDI M, PATTIPATI K, et al. A Generalized s-d Assignment Algorithm for Multisensory-Multitarget State Estimation[J]. IEEE Trans. on Aerospace and Electronic Systems, 1997, 33(2): 523-538.

[28]POPP R, PATTIPATI K R, BAR-SHALOM Y. An M-best s-d Assignment Algorithm and Parallelization with Application to Multitarget Tracking[J]. IEEE Trans. on Aerospace and Electronic Systems, 2001, 37(1): 22-39.

[29]KURIEN T. Issues in The Design of Practical Multitarget Tracking Algorithms. Multitarget-Multisensor Tracking: Advanced Application[M].Norwood,MA: Artech House, 1990.

[30]CHAN D S K, LANGAN D.A. Performance Results of The Bi-Level MHT Tracking Algorithm for Two Crossing Targets in A High Clutter Environment[C]∥SPIE Signal and Data Processing of Small Targets, Vol. 2235, 1994: 406-416.

[31]BLOSTEIN S D, RICHARDSON H S. A Sequential Detection Approach to Target Tracking[J]. IEEE Trans. on Aerospace and Electronic Systems, 1994, 30(1): 197-211.

[32]BLACKMAN S S, DEMPSTER R, REED R. Demonstration of Multiple Hypothesis Tracking (MHT) Practical Real-Time Implementation Feasibility[C]∥SPIE Signal and Data Processing of Small Targets, Vol. 4473, 2001: 470-475.

[33]NORMAN B K, CRONIN B A, BLACKMAN S S, et al. Adaptive Processing to Ensure Practical Application of A Multiple Hypothesis Tracking System[C]∥ SPIE Sensor, and Command, Control, Communications, and Intelligence Technologies for Homeland Security and Homeland Defense, Vol. 6201, 2006.

[34]de Feo M, GRAZIANO A, MIGLIOLO R, et al. IMMJPDA Versus MHT and Kalman Filter with NN Correlation: Performance Comparison[J]. IEE Proceedings, Radar, Sonar, Navigation, 1997, 144(2),: 49-56.

[35]KENNEDY H. Comparison of MHT and PDA Tracking Initiation Performance[C]∥IEEE International Conference on Radar, 2008: 508-512.

[36]BELLMAN R. Dynamic Programming[M].Princeton,NS: Princeton University Press, 1957.

[37]LARSON R E, PESCHON J. A Dynamic Programming Approach to Trajectory Estimation[J]. IEEE Trans. on Automatic Control, 1966, 11(3): 537-540.

[38]VITERBI A J. Convolutional Codes and Their Performance in Communication Systems[J]. IEEE Trans. on Communication Technology, 1971 , 19(1): 751-772.

[39]BARNIV Y, KELLA O. Dynamic Programming Solution for Detecting Dim Moving Targets Part II: Analysis[J]. IEEE Trans. on Aerospace and Electronic Systems, 1987, 23(6): 776-788.

[40]ARNOLD J, SHAW S, PASTERNACK H. Efficient Target Tracking Using Dynamic Programming[J]. IEEE Trans. on Aerospace and Electronic Systems, 1993, 29(1): 44-56.

[41]TONISSEN S M, EVANS R J. Performance of Dynamic Programming Techniques for Track-Before-Detect[J]. IEEE Trans. on Aerospace and Electronic Systems, 1996, 32(4): 1440-1451.

[42]JOHNSTON L A, KRISHNAMURTHY V. Performance Analysis of A Dynamic Programming Track Before Detect Algorithm[J]. IEEE Trans. on Aerospace and Electronic Systems, 2002, 38(1): 228-242.

[43]YI W, KONG L, YANG J,et al. A Tracking Approach Based on Dynamic Programming Track-Before-Detect[C]∥IEEE Radar Conference, 2009.

[44]YI W, MORELANDE R, KONG L, et al. Multi-Target Tracking Via Dynamic-Programming Based Track-Before-Detect[C]∥IEEE Radar Conference, 2012:487-492.

[45]PULFORD G W, La Scala B F. Multihypothesis Viterbi Data Association: Algorithm Development and Assessment[J]. IEEE Trans. on Aerospace and Electronic Systems, 2010, 46(2): 583-609.

[46]MAHLER R. A Unified Foundation for Data Fusion[C]∥SPIE Selected Papers on Sensor and Data Fusion, 1996.

[47]LIN L, BAR-SHALOM Y, Kirubarajan T. Data Association Combined with The Probability Hypothesis Density Filter for Multitarget Tracking[C]∥SPIE Signal and Data Processing of Small Targets, 2004:464-475.

[48]PANTA K, VO B N, SINGH S, et al. Probability Hypothesis Density Filter Versus Multiple Hypothesis Tracking[C]∥SPIE Signal Processing, Sensor Fusion and Target Recognition, 2004: 284-295.

[49]LIN L, BAR-SHALOM Y, KIRUBARAJAN T. Track Labeling and PHD Filter for Multitarget Tracking[J]. IEEE Trans. on Aerospace and Electronic Systems, 2006, 42(3): 778-795.

[50]PANTA K, VO B.N, SINGH S. Novel Data Association Schemes for The Probability Hypothesis Density Filter[J]. IEEE Trans. on Aerospace and Electronic Systems, 2007, 43(2): 556-570.

[51]DUNNE D, RATNASINGHAM T, LANG T, et al. SMC-PHD Based Multi-Target Tracking with Reduced Peak Extraction[C]∥SPIE Signal and Data Processing of Small Targets, 2009.

[52]ERDINC O, WILLETT P, BAR-SHALOM Y. A Physical-Space Approach for The Probability Hypothesis Density and Cardinalized Probability Hypothesis Density Filters[C]∥SPIE Signal and Data Processing of Small Targets, 2006.

[53]ERDINC O, WILLETT P, BAR-SHALOM Y. Probability Hypothesis Density Filter for Multitarget Multisensor Tracking[C]∥IEEE International Conference on Information Fusion, 2005: 25-29.

[54]MAHLER R. PHD Filters of Higher Order in Target Number[J]. IEEE Trans. on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.

[55]MAHLER R, EAGAN M. Second-Generation PHD/CPHD Filters and Multitarget Calculus[C]∥SPIE Signal and Data Processing of Small Targets, 2009.

[56]VO B T, VO B N, CANTONI A. Performance of PHD Based Multi-Target Filters[C]∥IEEE International Conference on Information Fusion, 2006: 1-8.

[57]VO B N, SINGH S, DOUCET A. Sequential Monte Carlo Methods for Multi-Target Filtering with Random Finite Sets[J]. IEEE Trans. on Aerospace and Electronic Systems, 2005, 41(3): 1224-1244.

[58]VO B N, MA W. The Gaussian Mixture Probability Hypothesis Density Filter[J]. IEEE Trans. on Signal Processing, 2006, 54(11): 4091-4104.

[59]MELZI M, OULDALI A. Joint Multiple Target Tracking Abd Classification Using The Unscented Kalman Particle PHD Filter[C]∥ IEEE International New Circuits and Systems Conference, 2011: 534-537.

[60]PACE M, ZHANG H. Grid Based PHD Filtering by Fast Fourier Transform[C]∥IEEE International Conference on Information Fusion, 2011: 1-8.

[61]杨峰, 王永齐, 梁彦，等. 基于概率假设滤波方法的多目标跟踪技术综述[J]. 自动化学报, 2013, 39(11): 1944-1956.

YANG Feng,WANG Yong-qi,LIANG Yan,et al.A Survey of PHD Filter Based Multi-target Tracking[J].Acta Automatica Sinica,2013,39(11):1944-1956.

[62]PUNITHAKUMAR K, KIRUBARAJAN T, SINHA A. A Sequential Monte Carlo Probability Hypothesis Density Algorithm for Multitarget Track-Before-Detect[C]∥SPIE Signal and Data Processing of Small Targets, 2005.

Review of Point Target Tracking Methods Based on Infrared Sensor

WANG Shuo1, ZHANG Yi-qun1，2，SUN Bing-yan3

(1.Beijing Inst. of Electronic System Engineering, Beijing 100854, China；2. Beijing Simulation Center,Seience and Technology on Special System Simulation Laboratory，Beijing 100854,China；3.Military Representitive office of the PLA in 23nd Research Institute of the 2nd Research Academy of CASIC,Beijing 100854,China)

Abstract:Common methods are reviewed to detect and track point targets. During the review of conventional tracking methods, such as global nearest neighbor (GNN), probabilistic data association (PDA), joint probabilistic data association (JPDA), multiple-hypothesis tracking (MHT), and dynamic programming algorithm (DPA), the differences and connections are discussed. The probabilistic hypothesis density (PHD) filter for multi-target tracking is also mentioned, and its superiority to other methods in performance is put forward. It is indicated that the improvements of DPA and PHD are possible research areas for further study.

Key words:Infrared point target; detecting; tracking; track-before-detect; Bayesian estimation; multi-target

*收稿日期：2015-05-26；修回日期：2015-05-28

基金项目：有

作者简介：王硕(1987-)，男，辽宁丹东人。博士生，主要研究方向为目标识别与信息融合。

通信地址：100854北京142信箱30分箱E-mail：13718854129@163.com

doi:10.3969/j.issn.1009-086x.2016.02.021

中图分类号：TN911.73

文献标志码：A

文章编号：1009-086X(2016)-02-0124-11