多飞行器协同被动时差定位误差传播特性及构型研究

张 东 黄雪梅 石晓荣

1.北京控制与电子技术研究所，北京100038 2.中国航天科工二院，北京 100039



多飞行器协同被动时差定位误差传播特性及构型研究

张 东1,2黄雪梅1石晓荣1

1.北京控制与电子技术研究所，北京100038 2.中国航天科工二院，北京 100039

以多飞行器协同远距离精确定位为背景，针对高速飞行器协同被动时差定位误差大的特殊问题，根据被动时差定位原理，推导出瞬时定位误差传播特性，根据误差传播特性提出改善定位精度的基站最佳空间构型。理论分析和数学仿真结果表明，描述误差传播特性的模型正确，在允许条件下取最长基线，且飞行器以保持最佳空间构型的协同编队飞行时，对目标定位精度最高。

多飞行器协同；时差定位；误差传播；最佳构型

被动定位系统本身不发射电磁波，因此隐蔽性好，能显著提高自身的生存能力，在现代战争中越来越受到重视[1-2]。其中，被动时差定位技术又是被动定位技术研究的重点[3]。现阶段的被动时差定位主要用在地面固定或车载基站对空中机动目标的跟踪定位方面[4-5]。现代战争是体系间的对抗，若充分利用多飞行器被动雷达的测量信息来提高远距离目标的被动定位精度，将减少飞行器上主动雷达暴露和被干扰概率，增强飞行器的生存能力和打击效果。由于高速飞行器具有高动态特性，因此其所载基站自身定位误差大，基站的相对构型不断变化，对目标定位精度有较大影响[6]。因此需要分析定位误差的传播特性以及找到定位精度最高的基站构型。

本文以对大中型舰艇、预警机中远距离精确定位为应用背景，以舰载、机载主动预警雷达为被动时差定位辐射源并作为研究对象。针对高速高动态飞行器基站自身定位的大误差特性，分析误差传播特性和基站构型对时差定位精度的影响，并找出定位精度最高的基站构型。对多飞行器协同远距离精确定位具有一定的参考意义。

1 被动时差定位原理

四站(O，A，B，C)被动时差定位原理为：辐射源辐射信号到达2个基站有时间差，根据这个时间差在空间可以确定1个以两基站为焦点的双曲面，4个基站的到达时间有3个独立的时间差，可以确定3个双曲面，这3个双曲面的交点即为目标点。被动时差定位根据时差的组合方式分为中心站法和非中心站法。中心站法中，基站间时差的配对方式为OA，OB和OC，基站O称为主基站，基站A，B，C称为副基站。以瞄准点的北天东坐标系为参考坐标系，在该坐标系中，目标T的位置为(x,y,z)，基站O的位置为(x0,y0,z0)，基站A，B，C的位置分别为(xi,yi,zi)，i=1,2,3，则定位方程[7]为：

(1)

其中，r0为目标到主基站O的距离，ri为目标到副基站的距离，Δri=ri-r0为距离差，Δti为时间差，c为光速。由式(1)可得：

AX=B

(2)

其中，

X=(ATA)-1ATB或X=A-1B

(3)

式(3)可用Chan算法和Taylor级数展开法求解[8]。

2 定位精度与误差传播特性分析

2.1 精度分析

由B的表达式和式(3)可以看出，时差测量误差和基站站址误差会引起定位误差，可得[9]：

dX=A-1·dB

(4)

目标定位误差协方差为：

P=cov(dX)=A-1·cov(dB)·A-T

(5)

由

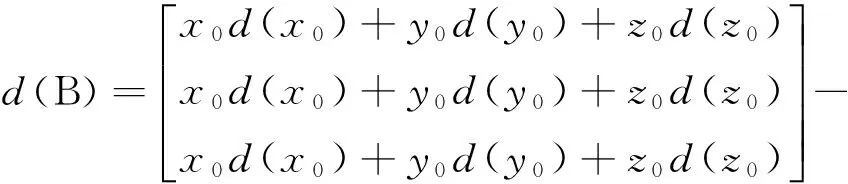
(6)

其中,d(Δri)=c·d(Δti)，i=1,2,3，d(Δti)表示时差测量误差。d(xi),d(yi),d(zi)，i=0,1,2,3，表示各基站三向站址误差。

设3个时差测量误差相互独立且均服从均值为0、标准差为σt的正态分布；各基站的三向站址误差相互独立且均服从均值为0、标准差为σs的正态分布；4个基站的自身定位相互独立；时差测量与基站自身定位相互独立。则式(5)可表示为：

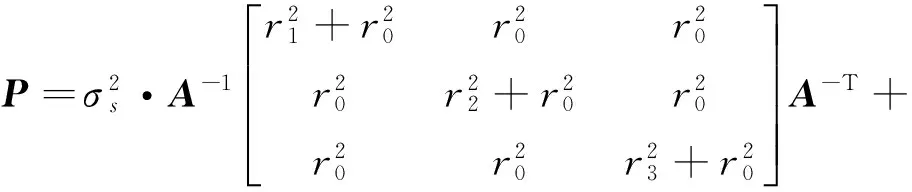
(7)

(8)

(9)

式(5)可简化为：

(10 )

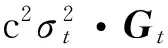
由此可以看出，定位误差σ与时差测量误差σt、站址误差σs、时差误差传递系数DOPt和位置误差传递系数DOPs有关。而DOPt和DOPs与基站位置矩阵A(基站空间构型和基站间距离)以及目标到基站的距离相关。

2.2 多飞行器协同下的误差传播特性分析

对于多飞行器协同被动时差定位，现有技术时差测量相当精确，可以达到σt≤30ns(转化为距离误差为cσt≤9m)[6]。当基站载体为采用惯性导航为主要导航手段的中远程高速再入飞行器时，其自身定位误差σs可达到公里级。

由式(8)和(9)可得：

(11)

因此有DOPs>DOPt。这种情况下，时差测量误差引起的定位误差DOPt·cσt相对站址误差引起的定位误差DOPs·σs是小量，可以忽略不计。则式(10)可简化为：

(12)

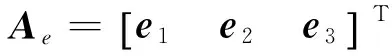
现做如下假设：

1)基站对称布局，有θ1=θ2=θ3=θ且l1=l2=l3=l。

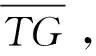
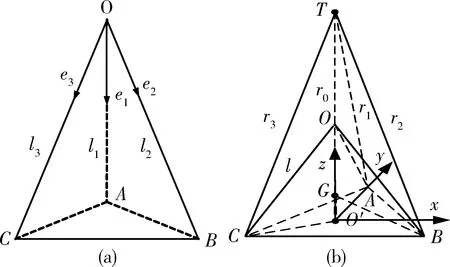
图1 被动时差定位空间关系图

目标T在O′O的延长线上。设a=r/l，为均距r与基线长l的比值。简化假设条件求得DOPs为DOPsg，则DOPsg/DOPs与a的关系如图2所示。

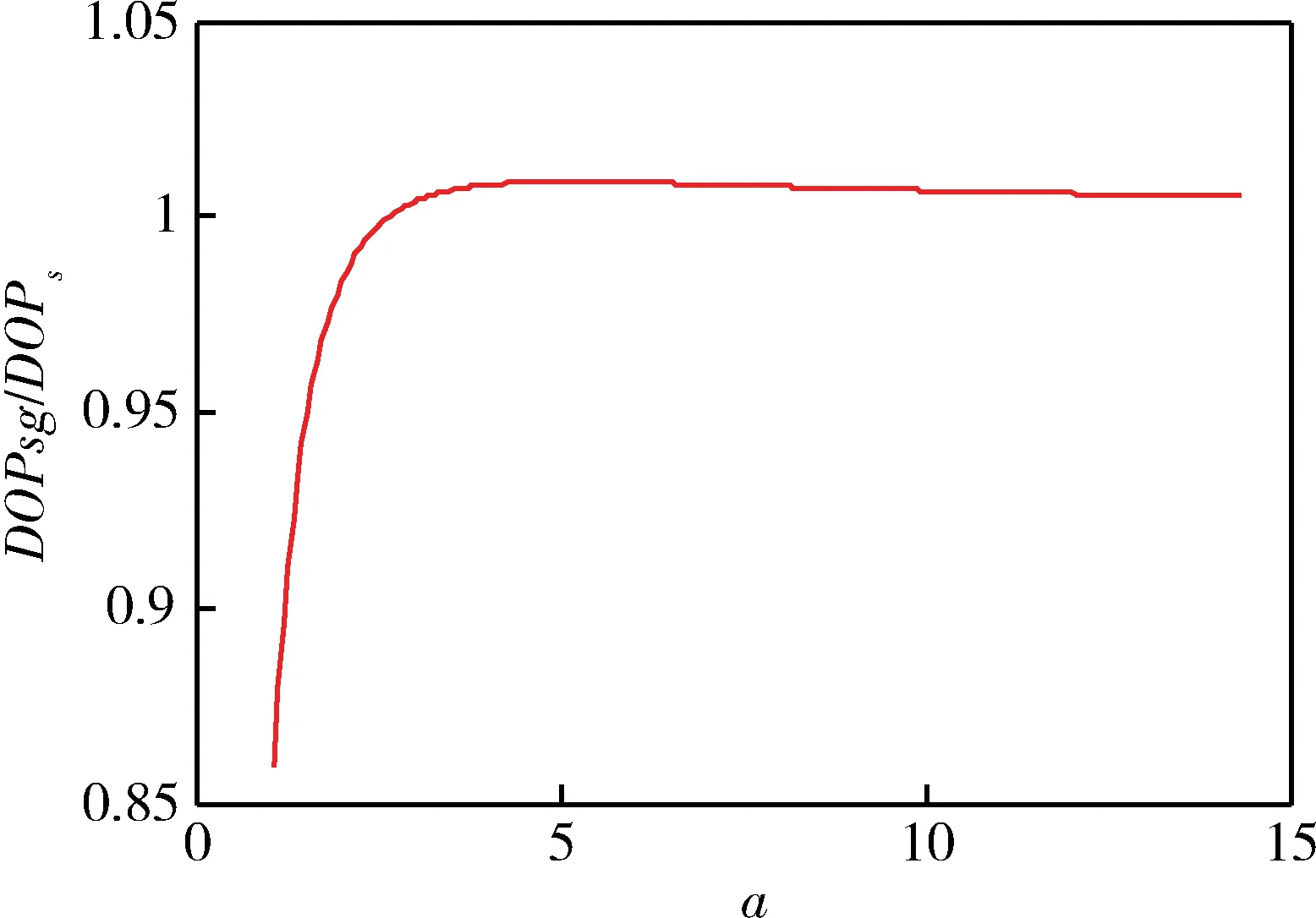
图2 DOPs简化误差与系数关系图

则Gs可写为：

(13)

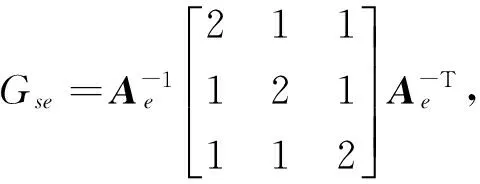
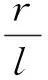
(14)

由此可以看出，在多飞行器协同被动时差定位中，当站址误差σs一定时，定位误差与基站构型有关，且与均距r成正比，与基线长度l成反比。基站构型对定位精度的影响将在下一节中分析。

3 最佳空间构型

为研究方便，建立以O站为原点的直角坐标系，使x轴和e1方向一致，e2在oxy平面内，且在y轴的分量为正。坐标系和单位矢量关系如图3所示。

图3 接收站连线矢量空间关系图

在上述坐标系下，单位构型矩阵可设为

(15)

由e1,e2,e3为单位矢量，满足

(16)

应用带拉格朗日待定系数(λ2,λ3)的函数F：

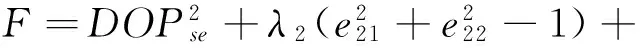
(17)

将F对i=e21,e22,e31,e32,e33分别求导并令其为0，结合式(16)，得到如下方程组：

(18)

式(18)所示方程组共有56组解，其中,满足-1≤eij≤1，i=2,3,j=1,2,3的解为需用解。需用解组成的单位构型矩阵Ae为：

(19)

式中，ei·ej=0.25，i,j=1,2,3,i≠j，这样的基站空间构型是任意两基线张角都为θ=75.5°。

因此，在基站对称布局且均距大于基线长度的2倍，基站的任意2个基线张角为75.5°时，定位精度最高。

4 仿真分析

仿真条件：目标在O′O延长线上，仿真参数设置如表1所示。10000次被动时差定位仿真，并对定位误差进行统计。

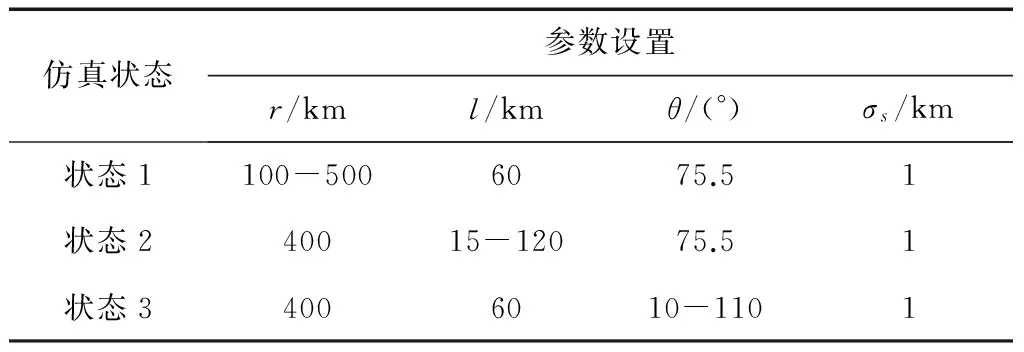
表1 仿真参数设置表

时差测量误差与站址误差对定位误差的影响如表2所示。位置误差传递系数DOPs和定位误差σ与均距r的关系如图4和5所示。位置误差传递系数DOPs和定位误差σ与基线长度l的关系如图6和7所示。位置误差传递系数DOPs和定位误差σ与基线张角的关系如图8和9所示。

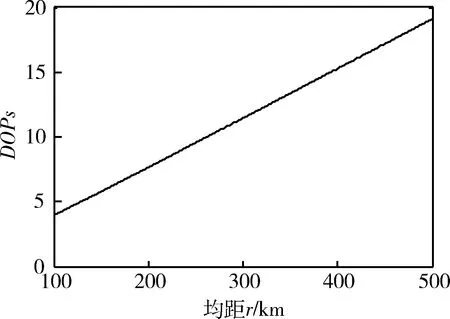
图4 位置误差传递系数与均距的关系

图5 误差与均距的关系

图6 位置误差传递系数与基线长度的关系

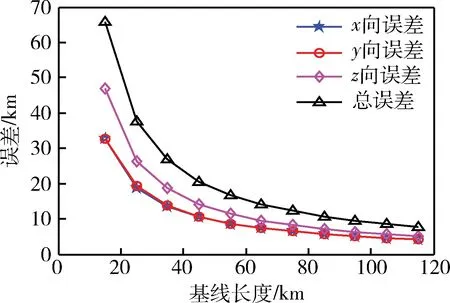
图7 误差与基线长度的关系

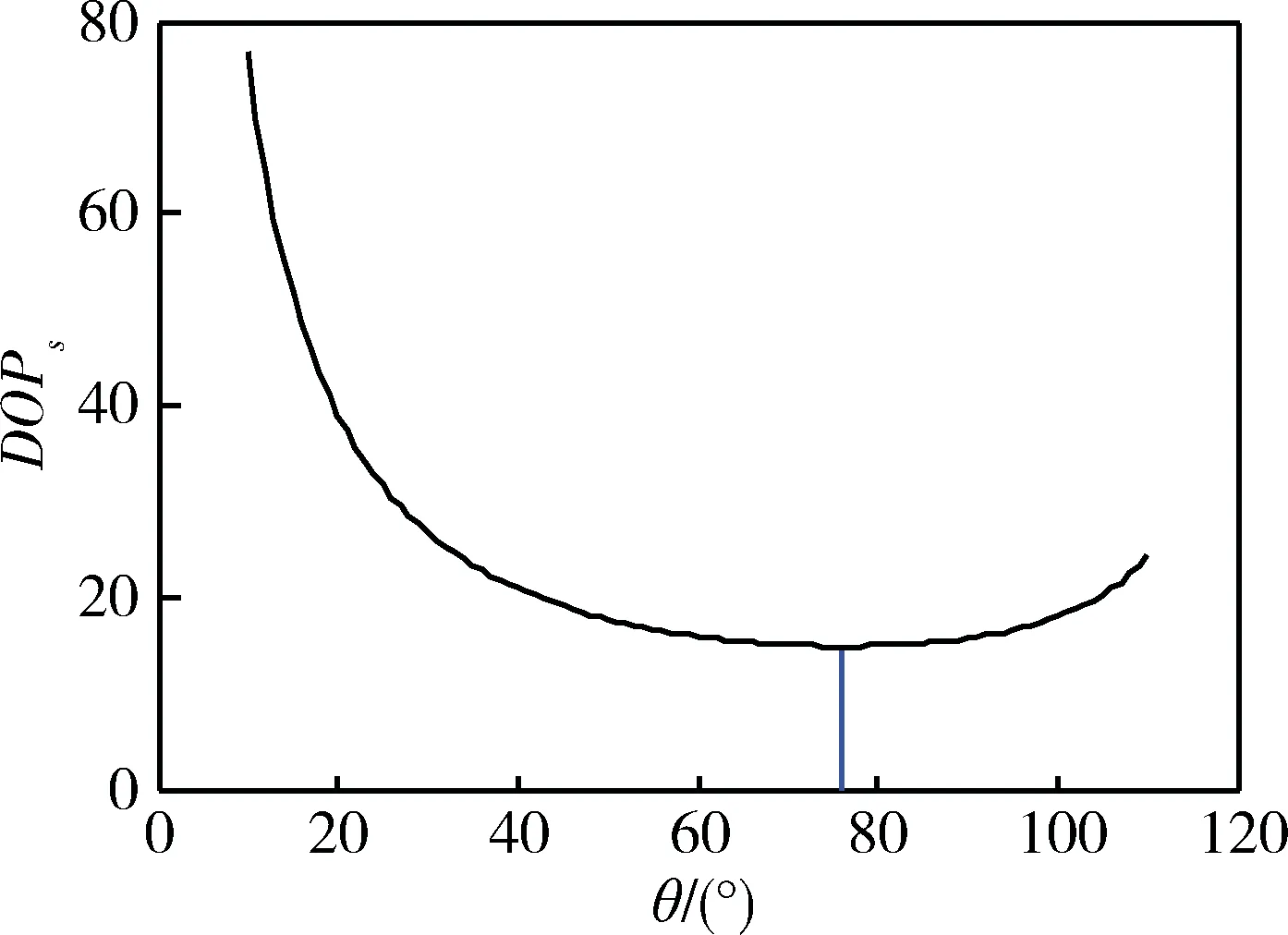
图8 位置误差传递系数与基线张角的关系

图9 误差与基线张角的关系

由表2可以看出，在多飞行器协同被动时差定位中，时差测量误差对定位误差的影响是小量，可以忽略不计，与理论分析一致。站址误差引起的定位误差σ可用σs·DOPs表示。

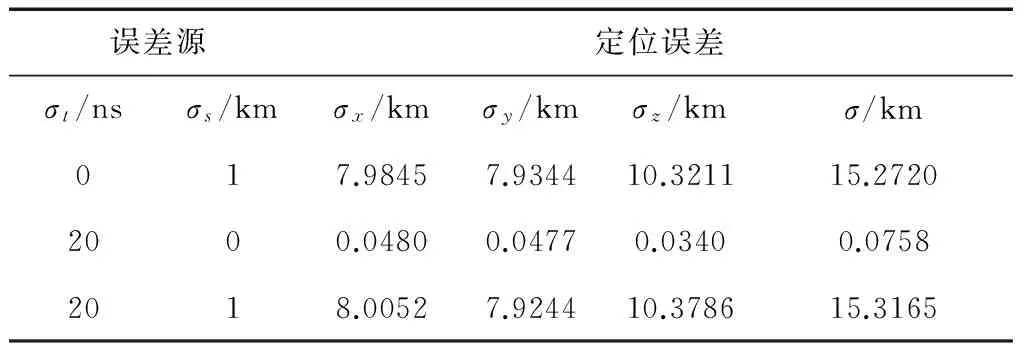
表2 定位误差统计表

由图4和5可以看出，定位误差与均距成正比。当均距大时，定位误差大；反之，定位误差小。由图6和7可以看出，定位误差与基线长度成反比，基线长度越长，定位误差越小；反之，定位误差越大，与理论分析一致。由图8和9可以看出，当基线张角均相等时，随着基线张角的增加，x，y向的定位误差减小，z向的定位误差增加，当θ=75.5°时，总的定位误差最小。验证了最佳空间构型的正确性。

因此，在允许条件下取最长基线长度，且高速飞行器以保持最佳空间构型的协同编队飞行时，对目标定位精度最高。

5 结论

在被动时差定位中，定位误差与时差测量误差、站址误差、基站空间构型、基站间距离以及目标到基站的距离相关。在多飞行器协同被动时差定位中，由于站址误差引起的定位误差较大，时差测量误差对定位误差的影响可以忽略。当站址误差σs一定时，定位误差与均距r成正比，与基线长度l成反比。当基站的几何配置为基线张角均为θ=75.5°的最佳空间构型时，目标瞬时定位精度最高。因此，在允许条件下取最长基线长度，且飞行器以保持最佳空间构型的协同编队飞行时，对目标定位精度最高。

[1] 孙仲康，周一宇，何黎星. 单多基地有源无源定位技术[M]. 北京: 国防工业出版社，1996.

[2] 胡来招. 无源定位[M]. 北京: 国防工业出版社，2004.

[3] 赵宏忠, 王桂岭, 谢良贵. 被动时差定位算法研究[J]. 现代防御技术,2007,35(1): 76-82.(Zhao Hongzhong, Wang Guiling, Xie Lianggui. Research on Passive Localization Estimate Algorithm of TDOA[J]. Modern Deffnce Thehnology, 2007，35(1): 76-82.)

[4] 陈玲，李少洪. 可消除定位模糊的被动时差定位算法[J]. 北京航空航天大学学报，2005, 31(1): 89-93 .(Chen Ling, Li Shaohong. Passive TDOA Location Algorithm for Eliminating Location Ambiguity[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(1): 89-93.)

[5] 王腾朝，杨靖雯，赵航生. “沉默哨兵”系统及其核心技术[J]. 军事通信技术，2009, 30(4): 89-93.(Wang Tengchao, Yang Jingwen, Zhao Hangsheng. Silent Sentry TM System and Its Core Technology[J]. Journal of Military Com munication Technology, 2009, 30(4): 89-93.)

[6] 王瀚. 机载多平台时差无源定位系统若干关键技术研究[D]. 长沙: 国防科学技术大学，2006.

[7] John D. Bard, Fredric M. Ham. Time Difference of Arrival Dilution of Precision and Application [J]. IEEE Transactions on Signal Processing ，1999, 47 (2). 521-523.

[8] 刘林，邓平，范平志．基于 Chan 氏算法和 Taylor 级数展开法的协同定位算法[J]．电子与信息学报,2004,26(1)：41-46.(Liu Lin, Deng Ping, Fan Pingzhi.A Cooperative Location Method Based on Chan and Taylor Algorithms[J]. Journal of Electronics&Information Technology,2004,26(1)：41-46.)

[9] 袁信, 愈济祥, 陈哲. 导航系统[M]. 北京: 航空工业出版社，1993.

Research on the Error Propagation and Configuration of Multi-Vehicle Cooperation Passive TDOA Location

Zhang Dong1,2，Huang Xuemei1， Shi Xiaorong1

1. Beijing Institute of Control and Electronics Technology，Beijing 100038，China 2.The Second Academy of China Aerospace，Beijing 100039，China

Basedonthebackgroundofmulti-vehiclecooperativelongdistanceaccuratepositioning,regardingthebigpositioningerroroccursduringthemulti-vehiclecooperationpassiveTDOAlocation,theruleofinstantaneouserrorpropagationisderivedfromtheprincipleofpassiveTDOAlocation.Inaddition,accordingtothecharacteriticsofinstantaneouserrorpropagation,theoptimizedconfigurationofbasestationisproposedforimprovingpositioningprecision.Theresultofmathematicalsimulationrevealsthatthemodelofinstantaneouserrorpropagationisrightandthelongestbaselineandhighesttargetpositioningprecisioncanbeobtainedwhileflightvehiclekeepsflyingincooperativeformationofoptimizedconfiguration.

Multi-vehiclecooperation; TDOAlocation;Errorpropagation;Optimizedconfiguration

2015-08-05

张 东(1990-)，男，四川南充人，硕士研究生，主要研究方向为导航、制导与控制；黄雪梅(1973-)，女，广东清远人，研究员，主要研究方向为导航、制导与控制；石晓荣(1977-)，女，西安人，研究员，主要研究方向为导航、制导与控制。

TN953

A

1006-3242(2016)03-0051-05