不确定收益的最优投资组合模型

韩　颖,杨夕涵,沈兰雅,钱家昌,张晓斌

(中国民航大学　理学院,天津　300300)



不确定收益的最优投资组合模型

韩颖,杨夕涵,沈兰雅,钱家昌,张晓斌

(中国民航大学理学院,天津300300)

[摘要]投资组合理论是金融学乃至整个经济学领域一个非常激动人心的部分,涌现出了大量的投资模型和理论,这些模型大多采用概率论或者模糊理论方法处理投资中的不确定性,对于缺乏样本数据这种情形(如购买的是新出现的证券)建立的模型甚少。针对这种投资情况,利用不确定理论考虑了马科维茨的均值——方差投资组合模型的变形形式,建立了不确定收益的最优投资组合选择模型,进一步丰富了证券投资理论。

[关键词]不确定理论；不确定规划；风险分析；投资组合

[DOI]10.13939/j.cnki.zgsc.2016.24.234

1952年,Markowitz[1]提出了著名的均值方差模型(MV)。均值-方差投资组合理论在研究方法上建立了衡量效用与风险程度指标,确定了资产组合的基本原则。Markowitz在其出版的《证券组合选择》一书中,详细论述了证券组合的基本原理,从而为现代西方证券投资理论奠定了基础。Markowitz资产组合理论研究的是多种资产的组合问题,根据这个理论,我们可以在方差一定的情况下,研究预期收益最大的投资组合问题；也可以研究预期收益一定情况下,方差最小的投资组合问题。

以往诸多投资分析的模型,往往以概率论方法处理投资中的不确定性,[2]而忽视了另一种不确定性—模糊性。事实上,金融市场有许多不确定性,例如受国家政策、突发事件,以及众多投资人的行为相互作用的影响。假设投资者欲购买新出现的证券(如股票),则没有或者有很少的样本数据可供统计分析,这时若用概率论方法及模糊理论方法处理该问题就显得力不从心。而刘宝碇于2007年建立的不确定理论[3]是处理此类问题的强有力工具,本文利用不确定理论给出了马科维茨均值方差模型的变形形式,即证券收益是不确定变量的情况。不确定理论是一个公理化的数学系统,假设读者已经熟悉了不确定理论的相关定义,如信度、不确定测度、不确定空间、不确定变量、(正则)不确定分布及相应的逆分布、期望、方差等,参考文献第一章和第二章。[4]

1相关引理

1.1引理一[4]

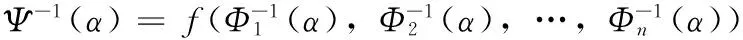
1.2引理二[5]

假设ξ1,ξ2,…,ξn是n个独立的不确定变量,且有正则的不确定分布分别是Φ1,Φ2,…,Φn,如果函数f(x1,x2,…,xn)相对于x1,x2,…,xm严格递增,相对于xm+1,xm+2,…,xn严格递减,那么不确定变量ξ=f(ξ1,ξ2,…,ξn)的期望。

1.3引理三[6]

假设ξ是一个独立的不确定变量,且有正则的不确定分布分别是Φ,和有限的期望e,则：

2期望收益一定下的最小风险投资组合模型

假设投资者欲购买n种新证券A1,A2,…,An,用xi(≥0)表示投资者在第i种证券上的投资额所占投资总额的比例,ξi表示第i种股票的收益率(i=1,2,…,n),由于所投资的n种新证券的收益没有样本数据可供统计分析,因此ξi服从不确定分布(分布函数由专家给出建议),投资者要在期望收益一定的情况下,要是投资风险达到最小,应如何选择投资比例？马科维茨的均值方差模型可转化为下面的形式：

(1)

式中，E表示期望值算子,V表示方差算子,b是投资者可以接受的最小期望收益率。

假设ξ1,ξ2,…,ξn是n个独立的不确定变量,且有正则的不确定分布分别是Φ1,Φ2,…,Φn,由引理一至引理三,上面的数学模型可以转化为下面的数学规划问题

(2)

3数值算例分析

假设投资者购买四种新出现的证券A1,A2,A3,A4；b=0.2。他向三位专家咨询每种证券的收益率,假设三位专家给出各种证券的收益率(假设权重相同)所满足的不确定分布如表1所示。

表1　证券收益率分布

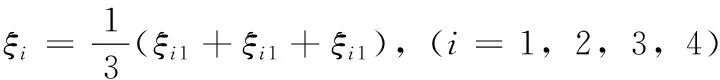
由引理二和引理三,根据模型(2)得：

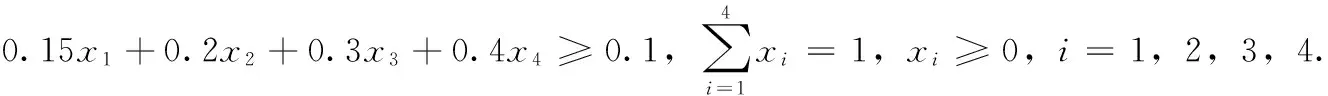
由Matlab7.0软件计算得出模型的最优解：(0.6667,0.3333,0,0),目标函数值为0.4778,即投资者在可以接受的最低收益率为0.1的前提下,按照上面的最优策略安排其投资比例,可达到最低风险0.4778。

4灵敏度分析

通过表2,我们看到,随着投资者可接受的最低收益率的逐步增大,他所要承担的最低风险也在逐步增大,符合“高回报,高风险”的规律。

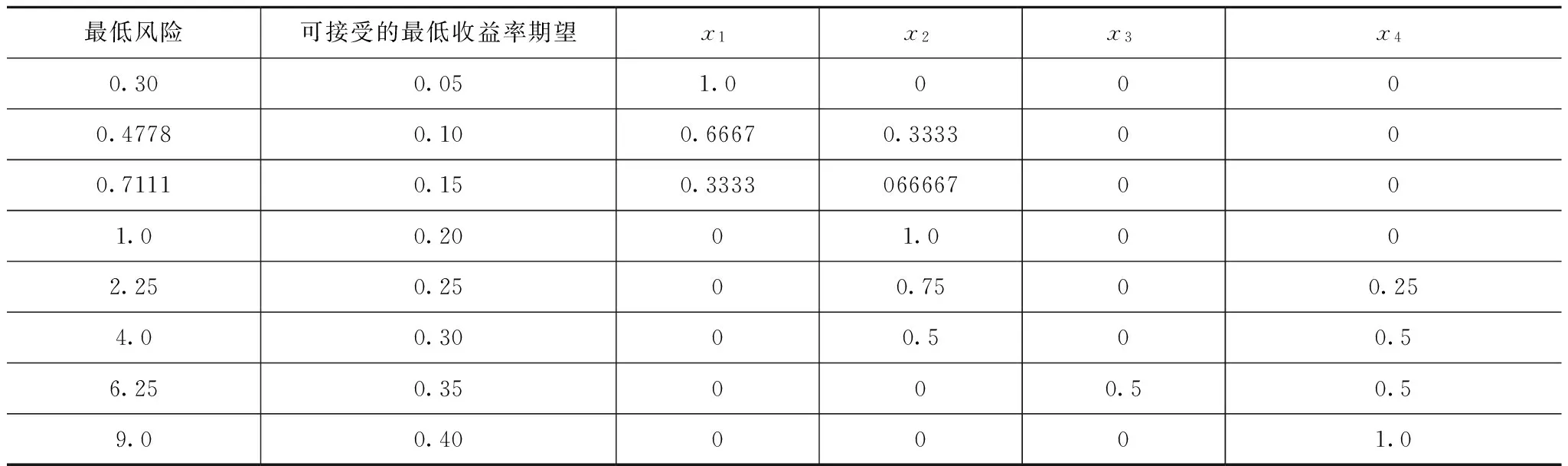
表2　最低风险与可接受最低收益率期望关系

5结论

针对投资者购买新出现的证券,缺乏历史数据可对证券收益率进行统计这种情况,本文利用不确定理论建立了不确定收益下的最优投资组合选择模型,得到了一个二次规划模型(2),并通过算例进行了投资模拟。通过采纳多位专家的意见,对专家给出的证券收益率所满足的不确定分布进行加权处理,使得投资风险进一步降低。下一步我们将研究投资者同时购买新出现的证券和已出现时间较长的证券的情况,即证券的收益率既有随机变量,也有不确定变量的情况。

参考文献：

[1]Markowitz H..Portfolio Selection[J].Journal of Finance,1952(7)：77-91,

[2]Konno H.,Yamazaki H..Mean-variance Deviation Portfolio Optimization Model and its Applications to Tokyo Stock Market[J].Management Science,1991,37(5):519-531.

[3]Liu B.D..Uncertainty Theory[M].2nd ed.,Berlin：Springer-Verlag,2007.

[4]Liu B.D..Uncertainty Theory[M].5nd ed.,Uncertainty Theory Laboratory,2015.

[5]Liu Y.H.,Ha M.H..Expected Value of Function of Uncertain Variables[J].Journal of Uncertain Systems,2010,4(3)：181-186.

[6]Yao K..A Formula to Calculate the Variance of Uncertain Variable[J].Soft Computing,2015,19(10)：2947-2953.

[基金项目]本文系(天津市级)大学生创新创业训练计划项目(项目编号：201510059044)相关研究成果。

[作者简介]韩颖(1994—),女,山西临汾人,中国民航大学本科生。研究方向:统计学；杨夕涵(1995—),女,陕西宝鸡人,中国民航大学本科生。研究方向：统计学；沈兰雅(1992—),女,天津人,中国民航大学本科生。研究方向：统计学；钱家昌(1994—),男,江苏南京人,中国民航大学本科生。研究方向：电子信息工程。通讯作者：张晓斌(1983—),男,山东蓬莱人,博士,中国民航大学讲师。研究方向：复分析,运筹与优化。