基于曲度特征的三维模型检索算法

周继来 周明全 耿国华 王小凤

摘要：针对如何提高复杂曲面的三维模型的检索精度的问题，提出了一种基于曲度特征的三维模型检索算法。首先，在模型表面选取随机采样点，计算点所在局部曲面的高斯曲率和平均曲率，通过高斯曲率和平均曲率求出随机点的曲度值，曲度值表明了曲面的凹凸属性。然后，以模型的质心为球心，以随机点与质心距离和曲度值为坐标轴建立坐标系，统计出一定距离范围内曲度值分布的概率，构建距离与曲度的分布矩阵，以此分布矩阵作为三维模型特征描述符。该特征描述符具有旋转不变性和平移不变性，能够很好地反映复杂曲面的几何特征。最后，通过比较分布矩阵给出不同模型间的相似度。实验结果表明，该方法相比形状分布算法的检索性能有较大提高，尤其适用于具有复杂曲面的三维模型检索。

关键词：

特征提取；曲度；高斯曲率；平均曲率；三维模型检索

中图分类号： TP391.72 文献标志码：A

0引言

三维模型库已经在机械制造、动画设计、分子生物、数字化考古等领域得到了广泛的应用。Internet的出现使三维模型的使用和传播变得非常便捷，三维模型库中的模型数量呈现出几何级数的增长，因此，如何从三维模型库中快速、有效地找到所需要的或相近的模型，已成为三维模型检索技术所要解决的核心问题[1-2]。

目前已有的基于内容的特征提取技术中，Osada等[3]提出了形状分布（Shape Distribution）算法（D2描述子），它的主要的优势是它的简便性，但是该方法对于复杂形状的模型区分度不高，由图1可以看出对于具有复杂曲面的模型D2算法提取的特征趋近相似。以D2算法为基础有诸多的改进，比如区分点对属性、加入点对间法相量夹角和点所在三角形的面积作为权值[4-6]等。这些方法对提高检索效率都有一定提高，但都不能有效反映复杂曲面的几何特征。周明全等[7]基于三维模型内部对称关系提出了一种空间对称描述符来表示三维模型的几何特征，该方法应用于具有对称特性的模型上取得了良好的检索效果，但检索效率有待提高。朱新懿等[8]利用三维模型的形状变化信息提取出形状特征描述符，如何选择模型切割方向对检索结果有较大影响。Torkhani等[9]提出了一种局部特征扩展锥曲率（extended conecurvature feature）并将其与提取的显著点和显著区域相结合计算三维模型的形状分布特征。Chen等[10]将局部曲面的曲率分布作为形状描述特征提取出来。Liu等[11]将曲面的内在曲率值作为特征描述符，包含了高斯曲率和平局曲率等反映模型局部曲面的几何性质，因此能够提高对于复杂形状的模型区分度。高斯曲率和平均曲率反映曲面局部的弯曲程度，但也有各自的不足之处，本身存在着对特定曲面不敏感问题。

本文提出一种基于曲度特征的三维模型检索算法，曲度特征计算当中包含了高斯曲率和平均曲率，能够较好地克服高斯曲率和平均曲率对特定曲面不敏感的不足，又能准确反映曲面的几何属性，因而能够提高模型检索的精度和准度。

1算法描述

空间曲面上的任意一点的曲率是描述三维模型形状的重要属性，它反映了点所在曲面的凹凸程度，具有旋转不变性和平移不变性。本文算法首先在模型表面选取随机采样点并计算点所在曲面的高斯曲率和平均曲率，通过高斯曲率和平均曲率求出曲度特征；然后以模型的质心为球心，以随机点的与质心距离和曲度值为坐标轴，统计出曲度值分布的概率，构建距离与曲度的分布矩阵；最后通过比较分布矩阵给出不同模型间的相似度。图2所示为3个模型曲度特征算法的检索过程。

1.1曲面曲率计算

算法所采用的Voronoi曲率估算方法是Meyer等[12]提出的，由文献[13]可知该方法相对于其他离散曲率估算法具有良好的稳定性和精确度。该方法的主要思想是：把光滑曲面看作是一族网格的极限或者是线性逼近，把三角网格每个顶点的度量性质看作是此空间网格在此点一个小邻域的平均度量。其主要步骤如下。

1）计算法矢量。

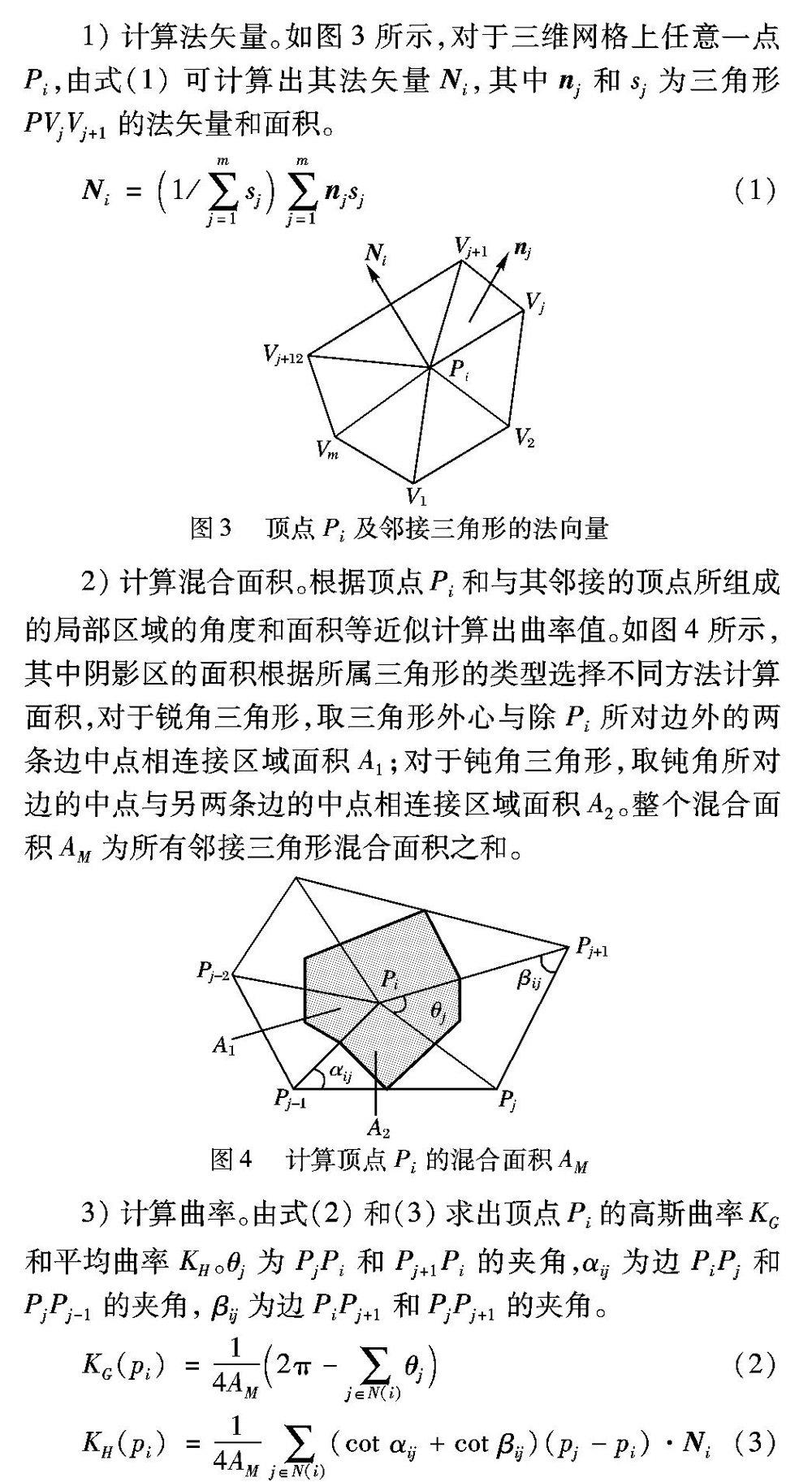
如图3所示，对于三维网格上任意一点Pi，由式（1）可计算出其法矢量Ni，其中nj和sj为三角形PVjVj+1的法矢量和面积。

如图3所示，三维网格上任意一点Pi计算法矢量Ni，nj和sj为三角形PVjVj+1的法矢量和面积，Ni为顶点Pi的法矢量。这句话不太通顺，请作相应调整。

2）计算混合面积。根据顶点Pi和与其邻接的顶点所组成的局部区域的角度和面积等近似计算出曲率值。如图4所示，其中阴影区的面积根据所属三角形的类型选择不同方法计算面积，对于锐角三角形，取三角形外心与除Pi所对边外的两条边中点相连接区域面积A1；对于钝角三角形，取钝角所对边的中点与另两条边的中点相连接区域面积A2。整个混合面积AM为所有邻接三角形混合面积之和。

1.2曲度计算

由微分几何[14]可知，高斯曲率和平均曲率能够反映曲面的几何不变量，它们表示点所在曲面局部的弯曲程度，但也有各自的不足之处，高斯曲率可以表示为最大主曲率k1和最小主曲率k2的乘积KG=k1×k2。当一个点在圆柱形曲面上时，它的最小曲率k2为值为0。由此可知，该点的高斯曲率值也为0，而平面的主曲率都为0，所以如果将高斯曲率作为特征提取，则其无法有效区分圆柱曲面和平面。平均曲率KH=（k1+k2）/2是最大主曲率与最小主曲率的和，当曲面存在鞍点时，该点平均曲率值为0，所以如果将平均曲率作为特征提取，其无法有效区分曲面上的鞍点和平面上的点。高斯曲率值和平均曲率都存在对特定的曲面不敏感的情况，如果单一使用会影响三维模型检索的精度和准度[15]，因此使用曲度作为一个特征值，计算式为：Cp=4K2H-2KG。

曲度值表示为高斯曲率和平均曲率差值的形式，当遇到圆柱曲面时，平均曲率值不为0，而遇到曲面上的鞍点时，高斯曲率值不为0，因此，曲度可以避免平均曲率和高斯曲率不足，其能够有效地区分圆柱形曲面点、鞍点和平面点。此外，当三维模型表面比较光滑时，曲面的平均曲率值比较小，以平均曲率作为特征描述符对此类模型的区分度不高，与之相比，高斯曲率则具有较好的识别度。另一方面，由于曲度是高斯曲率和平均曲率的差值，从而可以较好地克服高斯曲率在曲面上分布性对均匀的不足，所以曲度作为特征描述符能有效提高模型检索的精度和准度。

1.3计算随机点曲度

随机点选取采用D2算法的方式，经过实验，采样点的数量为5000时就可以达到比较理想的区分度。由于三维模型是以三角面片去近似逼近显示复杂曲面的，这样每个三角面片都具有曲度值，因此在选定随机采样点后可以使用式（4）计算该点的曲度：

1.4构建曲度分布矩阵

以模型质心为球心，模型的质心由式（5）求出。其中：p0为三维模型的质心；pi为模型的每个顶点坐标；N为顶点总数。pi到质心p0的距离为di，由此可以得到模型顶点到质心的最大距离dmax。

p0=1N∑Ni=1pi（5）

di=（xi-x0）2+（yi-y0）2+（yi-y0）2（6）下标是小写字符“o”，还是数字“0”？请明确。

以dmax为半径作包围球，将dmax等分为n份（n=50），d′=dmax/n，d′为距离增量。将曲度的最大值Cmax等分为m份（m=30）此处加了逗号，这样表述是否符合表达？请明确。C′=Cmax/m，C′为曲度增量。统计落入每个距离和曲度所对应的区间中随机采样点出现的概率，从而构成了一个30×50的特征矩阵。这样如图6所示构建出了三维模型曲面类型分布矩阵，该矩阵记录了不同距离区间上曲度的分布情况，由于更多地反映了模型几何形状信息，从而能有效地提高模型检索时的区分度。

1.5三维模型相似性度量

通过提取模型的曲面曲度信息将三维模型相似性度量转化为曲度分布矩阵之间的距离计算。相似性度量通常采用的方式为欧氏距离，欧氏距离的优点是计算简单，但缺点是在计算中它没有充分考虑到各个计算分量之间存在的相关性，使最终的产生结果会受到多个分量的干扰，导致比较精度的下降。为克服欧氏距离的不足，更好地反映矩阵所代表的模型间的相似度，采用Manhattan距离[16]，设U和V分别为两个模型的曲面类型分布矩阵，则U和V的相似性度量由式（7）计算得出：

D（U，V）=∑29i=0∑49j=0|uij-vij|（7）

2实验及结果分析

在使用Visual Studio 2010和OpenGL编程环境实现曲度特征（Curvedness Feature， CF）算法，实验平台为Intel i52400 3.10GHz CPU、4GB内存的IBM PC机。首先将CF算法与D2算法提取的特征进行对比，图7所示为5个模型的D2形状分布直方图和曲面类型分布矩阵。由表1中可以看出，三维模型蚂蚁和手、牛和兔子的形状直方图的曲线比较相似，但这些模型却有很大不同。这是因为D2算法只提取了模型的空间坐标距离信息，无法有效反映三维模型曲面的几何信息，而曲度特征包含了模型曲面的几何特征，因此对于具有复杂曲面的模型CF算法能够在反映三维模型几何特征上比D2算法有更高的区分度。

为验证算法的有效性，使用普林斯顿模型库（Princeton Shape Benchmark， PSB）[17]，从模型库中选取30类，每类10个模型，共300个模型进行实验。使用CF、D2、绝对角距离（AbsoluteAngle Distance， AAD）[18]和文献[8]并依照模型的相似性排序返回检索出的前7个最相近的模型。图8所示，CF算法由于选取的特征具有旋转、平移不变性，因而能有效地反映三维模型的整体形状特征和局部细节特征，提高检索结果的准确率。

为评价算法的检索性能，采用返回的F-1个模型中属于本类模型的比例（FirstTier， FT）（其中F为待检索模型所属类的模型个数），返回的2（F-1）个模型中属于本类模型的比例（SecondTier， ST），返回的第一个模型属于目标类的比例（Nearest Neighbor， NN）和增益值（Discounted Cumulative Gain， DCG）4种指标。由表1中的数据显示：CF算法的检索性能比D2算法有明显提高，从而证明CF算法具有良好的检索效果。

由图9可知，CF算法综合性能要优于D2、AAD和文献[8]的算法，这是由于本文算法将随机采样点所在局部曲面的几何信息和点相对于模型质心的距离信息集合在一起形成了分布矩阵，从而使具有复杂曲面的三维模型的几何特征能够更多地反映在提取的特征值中，且不需对3D模型的姿态进行预处理，而且由于算法采用的是在三维表面随机选择的点，使其对模型的简化和部分噪声具有不敏感性。

CF算法在三维模型表面用选取5000个随机点，每个点与模型质心的距离只需计算一次，而D2算法的1024点间的距离计算次数需要523776次，因此CF算法在距离计算阶段比D2算法要快。在进行特征值比较时，Manhattan距离计算的时间复杂度为O（n2），不过CF算法的特征值为50×30矩阵，因此CF算法的总体运行时间略少于D2算法。

3结语

曲度算法将高斯曲率和平均曲率作为模型特征提取出来，结合随机点的几何距离统计出分布的概率，构建曲度特征矩阵，通过比较曲度特征获得三维模型间的相似度。由于曲率性质具有旋转和平移不变性，因此不用预先对模型进行使用主成分分析法（Principal Component Analysis）等方法进行预处理。通过实验表明，CF算法对于具有复杂曲面的模型有较好的检索效果。下一步研究的方向是在已有工作的基础上寻找更有效的曲面特征提取方法和更高效的特征比较方法。

参考文献：

[1]

霍星，谭结庆.利用特征向量的三维模型检索[J].工程图学学报，2009，30（3）：76-79.（HUO X，TAN J Q.3D model retrieval based on feature vector [J]. Journal of Engineering Graphics， 2009， 30（3）： 76-79.）

[2]

徐士彪，车武军，张晓鹏.基于形状特征的三维模型检索技术综述[J].中国体视学与图像分析，2010，159（4）：439-450.（XU S B， CHE W J，ZHANG X P. A survey of 3D model retrieval based on shape features [J]. Chinese Journal of Stereology and Image Analysis， 2010，159（4）：439-450.）

[3]

OSADA R， FUNKHOUSER T， CHAZELLE B， et al. Shape distributions [J].ACM Transactions on Graphics， 2002， 21（4）： 807-832.

[4]

GAO Y， DAI Q H， ZHANG N Y. 3D model comparison using spatial structure circular descriptor [J]. Pattern Recognition， 2010， 43（3）： 1142-1151.

[5]

蒋立军，张旭堂，张广玉.基于面积分布算子的三维模型检索算法[J].计算机工程与应用，2012，48（12）：6-13.（JIANG L J， ZHANG X T， ZHANG G Y. 3D model retrieval method based on area distributions [J]. Computer Engineering and Applications， 2012， 48（12）： 6-13.）

[6]

SHIH J L， CHEN H Y. A 3D model retrieval approach using the interior and exterior 3D shape information [J]. Multimedia Tools and Applications， 2009， 43（1）： 45-62.

[7]

周明全，樊亚春，耿国华.一种基于空间对称变换的三维模型形状描述方法[J].电子学报，2010，38（4）：853-859.（ZHOU M Q， FAN Y C， GENG G H. A spatial symmetry descriptor for 3D model [J]. Acta Electronica Sinica， 2010， 38（4）： 853-859.）

[8]

朱新懿，耿国华.使用形状变化描述三维模型[J].计算机应用研究，2015，32（3）：922-925.（ZHU X Y， GENG G H. Shape variation representation of 3D shape descriptor [J]. Application Research of Computers， 2015， 32（3）： 922-925.）

[9]

TORKHANI F， WANG K， CHASSERY J M. A curvaturetensor based perceptual quality metric for 3D triangular meshes [J]. Machine Graphics & Vision， 2013， 32（16）： 1-25.

[10]

CHEN Q， YU Y M. 3D CAD model retrieval based on feature fusion [J]. Advanced Materials Research， 2013， 765/766/767： 316-319.

[11]

LIU Y J， ZHANG X D， LI Z M， et al. Extended conecurvature based salient points detection and 3D model retrieval [J]. Multimedia Tools and Applications， 2013， 64（3）： 671-693.

[12]

DESBRUN M， MEYER M， SCHRODER P， et al. Implicit fairing of irregular meshes using diffusion and curvature flow [C]// SIGGRAPH99： Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. New York： ACM， 1999： 317-324.

[13]

方惠兰，王国瑾.三角网格曲面上离散曲率估算方法的比较与分析[J].计算机辅助设计与图形学学报，2005，17（11）：17-23.（FANG H L， WANG G J. Comparison and analysis of discrete curvatures estimation methods for triangular meshes [J]. Journal of ComputerAided Design & Computer Graphics， 2005， 17（11）： 17-23.）

[14]

吴大任.微分几何讲义[M].北京：人民教育出版社，1984：126-128.（WU D R. Differential Geometry [M]. Beijing： Peoples Education Press， 1984： 126-128.）

[15]

屠宏，耿国华.一种基于局部特征的三维模型检索算法[J].计算机工程，2015，41（3）：218-222.（TU H， GENG G H. A 3D model retrieval algorithm based on local feature [J]. Computer Engineering， 2015， 41（3）： 218-222.）

[16]

DEJIAN V， VRANI C， DIETMAR S. An improvement of rotation invariant 3D shape descriptor based on functions on concentric sphere [C]// Proceedings of the 2003 IEEE International Conference on Image Processing. Piscataway， NJ： IEEE， 2003： 757-760.

[17]

SHILANE P， MIN P， KAZHDAN M， et al. The Princeton shape benchmark [C]// SMI04： Proceedings of the 2004 International Conference on Shape Modeling and Applications. Washington， DC： IEEE Computer Society， 2004： 167-178.

[18]

OHBUCHI R， MINAMITANI T， TAKEI T. Shapesimilarity search of 3D models by using enhanced shape functions [C]// TPCG03： Proceedings of the Theory and Practice of Computer Graphics 2003. Washington， DC： IEEE Computer Society， 2005： 97-104.