δ-正规空间中的一些性质

苏　丽

(大连科技学院 基础部, 辽宁 大连　116052)



δ-正规空间中的一些性质

苏丽

(大连科技学院 基础部, 辽宁 大连116052)

摘要：定义了与δ-正规空间有关的一些拓扑性质,并进行了初步的研究，主要讨论了拓扑空间的非空子空间的性质。

关键词：δ-正则； 超δ-正则； δ-正规； 强δ-正规； 几乎δ-正规

1基本概念

首先，在这里给出文中所涉及的一些基本概念。

为了方便，在文中X表示拓扑空间，Y为X的非空子空间。

定义1称空间X是δ-正规的是指如果X中的每一对不相交的闭集A,B存在X中不相交的Gδ-集U,V使得A⊂U,B⊂V。

定义2称空间X是δ-正则的是指对X中任意一点x和不含x的闭集B存在X中不相交的Gδ-集U,V使得x∈U，B⊂V。

注:类似于定义Y在X中正规等的相对拓扑思想,下面给出δ-正规空间中的一些相对拓扑的定义[1]。

定义3称Y在X中δ-正则是指如果对∀y∈Y和X中任意不含y的闭子集B,都存在X中不相交的Gδ-集U,V使得y∈U,B∩Y⊂V。

定义4称Y在X中δ-正规是指如果对X中不相交的闭集A,B存在X中不相交的Gδ-集U,V使得A∩Y⊂U,B∩Y⊂V。

定义5称Y在X中几乎δ-正规是指如果对X中每一对不相交的闭集A,B，存在Y中不相交的Gδ-集U,V使得A∩Y⊂U,B∩Y⊂V。

定义6称Y在X中强δ-正规是指如果对Y中每一对不相交的闭集A,B存在X中不相交Gδ-集U,V使得A⊂U,B⊂V。

定义7称Y在X中超δ-正则是指如果对每一个y∈Y和不含y的闭子集B,存在X中不相交的Gδ-集U,V使得y∈U,B⊂V。

定义8称Y在X中强δ-正则是指对∀y∈X 和X中闭集P,且x∉P,都存在X中不相交的Gδ-集U,V使得x∈U,P∩Y⊂V。

定义9 设X是一个拓扑空间,如果X的每一个开覆盖都有一个可数子覆盖,则称拓扑空间是一个lindelöf空间。

定义10称Y在X中lindelöf是指如果对X的任意开覆盖,都存在可数的子族γ,使得Y⊂∪γ。

2主要结论及其证明

引理1假设M⊂X,且M是X上Gδ-子集,如果A⊂M,那么A是M的Gδ-子集,当且仅当A是X上Gδ-子集。

证明此引理参阅文献[2-4]。

定理1若Y是X的Gδ子空间, Y在X中δ-正则⟺Y是δ-正则空间。

证明“⟹”Y在X中δ-正则,对Y中的点y及Y中的闭集P，使得y∉P， 存在X中的闭集A，使得P=A∩Y，因为Y在X中δ-正则,那么存在X中的不相交的Gδ-集U，V使得y∈U，P=A∩Y⊂V，而P=A∩Y∩Y⊂V∩Y，又因为y∈U，y∈Y，所以，y∈U∩Y，P⊂V∩Y,而U∩Y,V∩Y是Y中不相交的Gδ-集，由定义知Y是δ-正则的。

“⟸” 取y∈Y, Y中闭集P, y∉P, 存在Y中不相交的Gδ-集U,V使得y∈U, P⊂V,由于Y是X的Gδ-子空间,由引理1知,U,V是X的Gδ-集,存在X中不相交的Gδ-集U′,V′使得U=U′∩Y。V=V′∩Y，所以y∈U=U′∩Y，P⊂V=V′∩Y,那么y∈U′,P∩Y⊂V∩Y=V′∩Y∩Y=V′∩Y⊂V。

定理2Y是X的既开又闭的Gδ-子空间,则Y在X中δ-正则⟺Y在X中超δ-正则。

证明“⟸”显然[5-6]。

“⟹”已知Y在X中δ-正则,对∀y∈Y及X中闭集P,使得y∉P,存在X中不相交的Gδ-集U,V使得y∈U,P∩Y⊂V,因为y∈Y,所以y∈U∩Y 而Y为X的开Gδ-子空间，那么U∩Y为X的开Gδ-子集。令U′=U∩Y，又已知Y是X的闭Gδ-子空间，故X-Y为X开Gδ-子集。

令V′=V∪(X-Y)，则P⊂V′，故Y在X中超δ-正则。

定理3若Y为X的闭Gδ-子空间，Y在X中几乎δ-正规⟺Y是δ-正规空间。

证明“⟸”证明略[7]。

“⟹”对Y中任意两个闭集A，B且A∩B=φ，Y为X的闭Gδ-子空间，所以A，B为X的闭集，即A⊂X，B⊂X，因为Y在X中几乎δ-正规，存在Y中不相交的Gδ-集U，V，使得A∩Y⊂U，B∩Y⊂V，而A=A∩Y，B=B∩Y，即A⊂U，B⊂V，于是证得Y是δ-正规空间。

推论1若拓扑空间Y为X的闭的Gδ-子空间，则下面命题等价。

1)Y在X中几乎δ-正规。

2)Y在X中δ-正规。

3)Y在X中强δ-正规。

推论2设X,Y,Z为拓扑空间，若Y⊂Z⊂X则有:

1)Y在X中δ-正规，Z为X的Gδ-闭子空间⟹Y在Z中δ-正规。

2)Y在Z中强δ-正规,Z为X的Gδ-子空间⟹Y在X中。

3)Y在X中几乎δ-正规, Z为X的闭子空间⟹ Y在Z中几乎δ-正规。

证明只需证明1),2)和3)的证明方法类似[8]。

因为Z为X的闭的Gδ-子空间,所以∀A,B⊂Z,A∩B=φ,若A,B为Z-闭集,则A,B为X-闭集,又因为Y在X中δ-正规。所以存在X中的Gδ-集U′,V′使得A∩Y⊂U′,B∩Y⊂V′,令U=U′∩Z,V=V′∩Z,则A∩Y⊂U,B∩Y⊂V,于是Y在Z中δ-正规。

定理4Y在X中强δ-正则，Y在X中lindelöf,且Y为X的Gδ-子集，则Y在X中δ-正规。

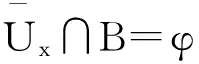
Y在X中lindelöf,存在可数集A1⊂A,使得

那么

所以

同理有

由强δ正则的定义知存在不相交的Gδ集U,V对于x∈A,x∉B,而B⊂X-A,那么

由此可以推出

A∩Y⊂Y-V

同理

B∩Y⊂Y-U

又因为Y为X的Gδ子集，因此Y在X中δ-正规[6]。

参考文献：

[1]Engelkingr.Generaltopology[M].Warszawa:PWN-PolishScientificPublishers,1977:45-106.

[2]ADow,JVermeer.Anexampelconcerningthepropertyofaspacebeinglindelofinanother[J].TopologyAppl.,1993(51):255-260

[3]严维军,王延庚.相对拓扑的一些性质[J].纯粹数学与应用数学,1999(4):223-226.

[4]腾辉.积空间的正规性及其相关性质[D].成都:四川大学,1999.

[5]彭良雪，王尚志.几种新空间类的性质及其相互间的关系[J].首都师范大学学报:自然科学版，1999(3):4-7.

[6]李庚雷.Somepropertiesofrelativetopologicalspace[J].吉林师范大学学报,2005(3):87-88.

[7]汪贤华,王延庚,卫国.相对拓扑空间的一些性质[J].西北大学学报,2003,33(2):133-136.

[8]胡永力,王尚志,彭良雪.相对拓扑中的两个问题[J].纯粹数学与应用数学,2000(3):76-77.

Somepropertiesofδ-normalspaces

SULi

(DepartmentofBasic,DalianInstituteofScienceandTechnology,Dalian116052,China)

Abstract：Sometopologicalpropertiesrelatedwithδ-normalspacearedefined.Thepropertiesofnon-emptyspaceintopologicalspacesarediscussed.

Keywords：δ-regular;superδ-regular; δ-normal;stronglyδ-normal;almostδ-normal.

收稿日期：2016-03-23

基金项目：辽宁省教育科学“十二五”规划(青年科研骨干专项JGZXQDB038)

作者简介：苏丽(1981-)，女，汉族，吉林通化人，大连科技学院讲师，硕士，主要从事一般拓扑学方向研究,E-mail:suli_ye05118@sina.com.

DOI:10.15923/j.cnki.cn22-1382/t.2016.3.03

中图分类号：O189.1

文献标志码：A

文章编号：1674-1374(2016)03-0221-03