基于SAS的回归分析异方差的检验与消除

王纯杰，　郑　茜，　李　群，　林珊屹

(长春工业大学 基础科学学院， 吉林 长春　130012)



基于SAS的回归分析异方差的检验与消除

王纯杰，郑茜*，李群，林珊屹

(长春工业大学 基础科学学院， 吉林 长春130012)

摘要：利用SAS软件的REG过程步实现了回归分析中异方差的White检验，利用加权最小二乘法消除了异方差的影响。通过与残差图法和等级相关系数法的结果比较，该检验效果更精确。利用2013年全国31个省市自治区保险赔付和保费数据进行实证分析。

关键词：回归分析； 异方差检验； 加权最小二乘估计

0引言

根据回归分析中最小二乘估计的结果，可以得到自变量与因变量之间的关系，但是模型中可能存在整体模型或者个别变量不显著的情况，由多种原因导致，如异常值与强影响点，多重共线性等。异方差是常见原因之一，消除异方差可以使模型显著。异方差问题分为两大类，即异方差的诊断和消除。关于异方差诊断，常见的方法有残差图检验法和斯皮尔曼等级相关系数检验法。这两种方法可以判定是否存在异方差，但是它们有一定的局限性，可见探索其他的方法很有意义。

1回归方程和普通最小二乘估计[1]

用y表示因变量，X=(X1,X2,…,Xp)T是对y有影响的p个自变量，回归模型一般表述为:

(1)

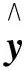
(2)

即

(3)

回归模型的基本假设如下：

1)E(ε)=0，var(ε)=σ2I;

2)E(X′ε)=0;

3)rank(X)=p+1。

于是有E(y)=Xβ,cov(εi,εj)=σ2，线性回归模型简记为(y,Xβ,σ2In)[1]。

定义离差平方和

(4)

回归系数β的估计为

回归方程的估计式为:

(5)

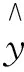
根据模型假设，回归模型要检验3个方面：

1)回归模型的显著性；

2)每个自变量的显著性；

3)残差是否为“纯随机”。

2 异方差的检验

2.1异方差产生的原因和影响

经典回归假设中一个重要的假设是var(εi)=σ2，即扰动项的同方差性。当模型中随机扰动项的方差不是常数时，称为异方差或方差非齐性。记为：

(6)

随机误差项包含众多因素对解释变量的影响，如果它们随着解释变量观测值的变化而变化，则会对解释变量产生影响。异方差现象存在时，参数估计值虽然是无偏的，但不是有效的，即不再具有最小方差性。以一个简单线性回归模型为例，模型如下:

(7)

对回归系数β1进行普通最小二乘(OLS)估计，可得:

(8)

(9)

(10)

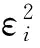
(11)

则

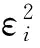
(12)

则

2.2异方差的检验

关于异方差性的检验[2]，统计前辈们进行了大量的研究，提出的诊断方法很多，但是没有一个公认的最好的方法。下面先介绍一下残差图分析法和等级相关系数法，这是两种比较常见的方法[2]。

2.2.1残差图分析法

残差图分析法非常简单、直观，它是一种非正式的检验方法。如果在检验前不能判断是否存在异方差，可以采用该法。做法是先不考虑存在异方差的假定下构造回归模型,然后以残差ei为纵坐标，以其他合适的变量为横坐标，画散点图。常用的横坐标有3种：

1)以解释变量xi(i=1,2,…,p)为横坐标；

3)以观测值或序号为横坐标。

如果回归模型适合样本数据，那么残差ei应该反映εi所假定的性质，即残差图上的n个点应该是随机分布和没有任何规律的。如果回归模型存在异方差，残差图上点的分布会呈现一定的趋势，如残差ei的值随y值的增大而增大(或减小)，具有明显的规律，由此可以判断模型的随机误差项εi的方差是非齐性的，存在异方差。

2.2.2等级相关系数法

等级相关系数法又称斯皮尔曼(Spearman)检验，是一种应用比较广泛的方法。进行等级相关系数检验有3个步骤：

1)求出y关于x的普通最小二乘估计，求出εi的估计值，即ei的值。

2)取ei的绝对值，即|ei|，把xi和|ei|按递增(或递减)的次序排列，分成等级，按下式计算等级相关系数:

(13)

式中:n----样本容量;

di----对应xi和|ei|的等级的差数。

3)做等级相关系数的显著性检验。在n>8的情况下，用下式对样本等级相关系数rs做t检验，检验统计量为:

(14)

2.2.3White检验

(15)

(16)式中：n----观测值的个数;

p----回归参数的个数，包括常数项。

(17)

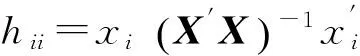
(18)

研究发现，当样本量小于250时，HC3的性质最优。

在SAS中,可以通过在model语句后面加入HCCMETHOD=0(,1,2,3)选项来选择异方差性相容协方差矩阵的估计方法，默认选项是HC0。

model语句后面的ACOV选项的作用是在参数估计的结果中显示异方差性相容协方差矩阵，而且增加了异方差性标准差，就是White标准差。如果在model语句后面选择了HCC选项或者WHITE选项，但是没有选择ACOV选项，结果中会显示异方差性标准差，但是不会显示异方差性相容协方差矩阵。SPEC选项是对模型做一个检验，原假设是回归估计的误差项,是独立同方差的。备择假设是误差项具有异方差。可以指定model语句后面的SPEC，ACOV，HCC，White选项，来选择检验的类型，检验给出的一致协方差矩阵都是渐近的。ACOV选项和SPEC选项可以用在model语句或者print语句中。

3异方差的消除

如果模型存在异方差，就违背了回归模型的基本假定，不能使用普通最小二乘法估计参数了。如果对原有的模型进行变换，使其满足同方差性的假设，再进行参数估计，可以得到理想的模型。最常用的方法是加权最小二乘法[4]。

3.1加权最小二乘估计

假设观测数据y与参数β1,β2，…，βp之间服从如下线性关系:

(19)

其中,ε是扰动项，进行n次观测可以得到n个线性方程:

(20)

式(20)可以用矩阵表达，即:

(21)

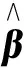
(22)

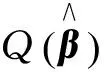
(23)

令式(23)为0，解得:

(24)

式(24)就是最小二乘估计的表达式，它与观测数据y和系数阵X有关[5]。

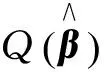
(25)

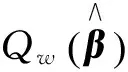
(26)

解得:

(27)

3.2加权最小二乘估计权数的确定

加权最小二乘估计误差的方差推导过程如下：

(28)

我们的目标是求出使式(28)达到最小的w, 即加权系数，由此引入矩阵型许瓦兹不等式。

定理1设A,B分别为m×n和n×l矩阵，且AAT是可逆矩阵，则有：

(29)

当且仅当存在一个m×l维矩阵P，使得B=ATP时式(29)取等。

证明：

BTB-2BTAT(AAT)-1AB+BTAT(AAT)-1AAT(AAT)-1AB=

(30)

所以BTB≥(AB)T(AAT)-1AB得证。

当且仅当B=AT(AAT)-1AB时,式(30)右端为零矩阵。令P=(AAT)-1(AB)，有B=ATP；反之,如果B=ATP，则有AT(AAT)-1AB=AT(AAT)-1AATP=ATP=B，由此证明了式(28)中等号成立的充要条件是B=ATP，证毕。

下面利用这个定理求加权系数。因为var(ε)=σε是对称的正定矩阵,令σε=PTP,其中P为n×n的可逆矩阵。取l=n,令A=XTP-1,B=PwX(XTwX)-1,可以看出AB=1,所以对任意的加权矩阵可以得到如下不等式：

BTB≥

(31)

比较式(31)的两边，有

(32)

此时加权最小二乘估计的误差方差达到最小,即：

(33)

此时的估计为：

(34)

3.3加权最小二乘估计的步骤

1)将回归方程的各项除以比例因子Zi，得到新的回归方程，同时满足误差项的同方差性；

2)对新回归方程进行最小二乘估计，求得回归参数。

4实证分析

SAS系统(Statistics Analysis System)的重要组成部分和核心功能是统计分析，最新版本是9.4版。 SAS可以提供多个统计分析过程，每个过程均含有丰富的选项，满足客户的不同需求[6]。

若想对某一实际现象作回归分析，首先要检验数据是否存在异方差现象，然后选择合适的方法进行消除，最后观察模型拟合数据的程度。2013年全国31个省市自治区保险保费收入和赔付支出情况见表1。

表1　2013年全国31个省市自治区保险保费收入和赔付支出情况

文中利用的数据是2013年全国31个省市自治区保险赔付支出和保费收入的数据，该数据是横截面数据(来自中国统计年鉴，2014)。设保费收入为自变量x，赔付支出为因变量y，单位是亿元，由此建立回归模型，分析自变量对因变量产生的影响。

在进行回归分析之前，需要先进行相关分析，利用SAS软件的CORR过程步可以实现。因变量支出与自变量收入的相关系数是0.989 75，在显著性水平为0.05下，通过检验，说明自变量与因变量之间有很大的相关性, 可以进行回归分析[7]。 SAS程序如下：

data expend2013;

input expend income;

cards;

318.17994.44

102.00276.80

…

24.0472.70

106.59273.49

;;

proc corr data=expend2013;

run;

proc reg data=expend2013;

model expend=income;

output out=expend2013_r r=residual;

run;

quit;

普通回归分析结果见表2。

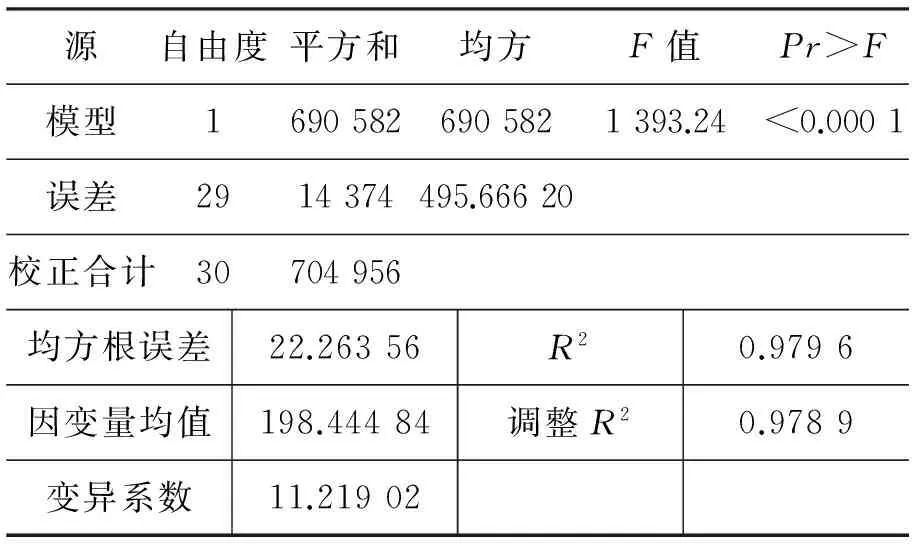
表2　方差分析表

因为数据的单位小，每个变量的值很大，所以导致总平方和、离差平方和、回归平方和都很大，F值为1 393.24，P值<0.000 1，表明回归方程高度显著，说明自变量对因变量有高度显著影响。通过复决定系数R2=0.979 6，也可以判定回归方程高度显著。在显著性水平为0.05以下，自变量的t检验通过了，说明它对因变量有显著影响，常数项也通过了检验，下面开始检验异方差[8]，SAS程序如下：

proc gplot data=expend2013_r;

plot residual*income=1;

symbol1 c=blue v=circle i=none;

label income="保费" residual="残差";

run;

残差关于自变量收入的散点图如图1所示。

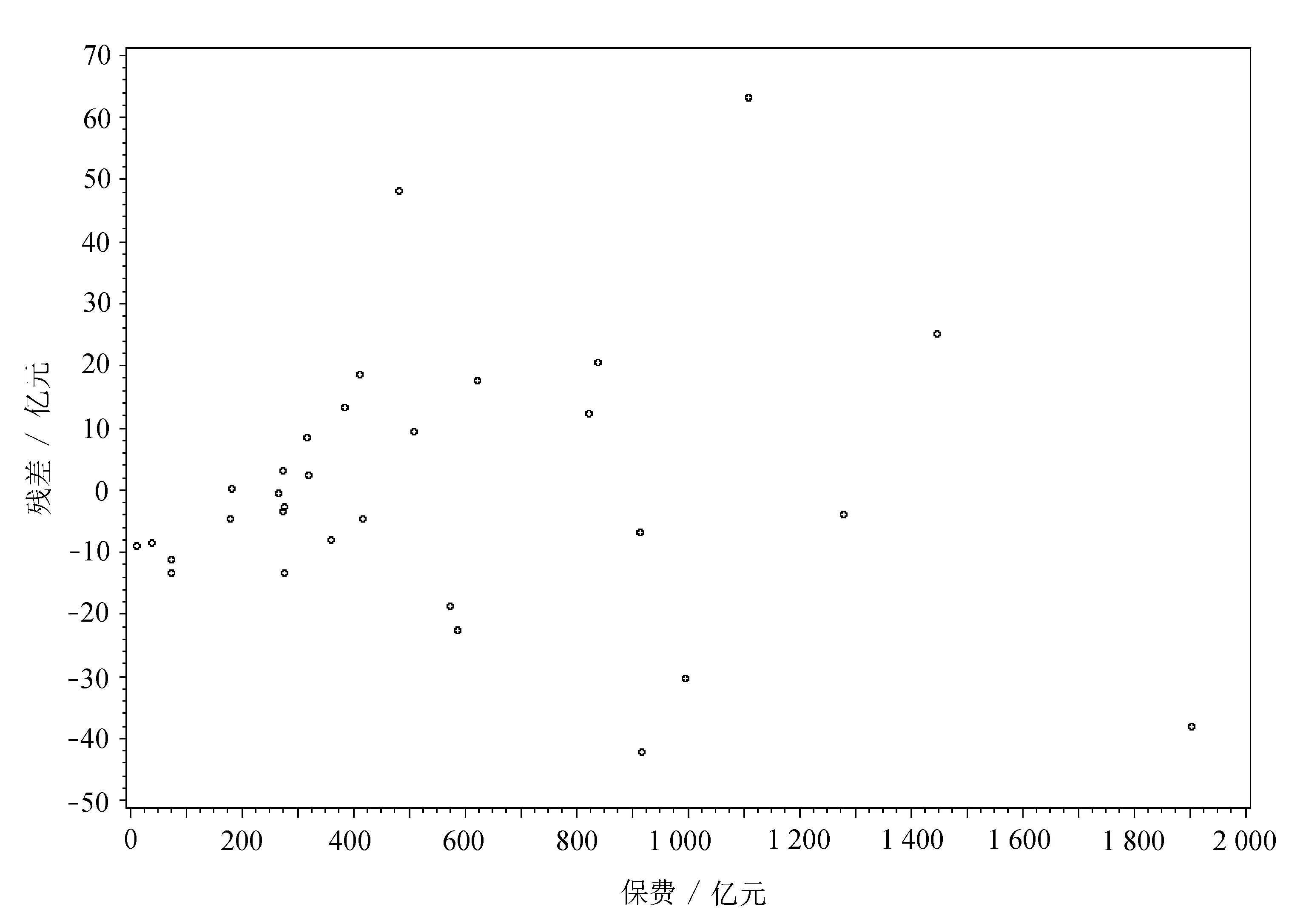
图1残差图

可以看出残差不是随机分布的，有向外扩张的趋势，初步判定存在异方差现象。下面进行等级相关系数检验，程序如下：

data r2013_abs;

set expend2013_r;

abs_r=abs(residual);

run;

proc corr data=r2013_abs spearman;

var abs_r income;

label income="保费" abs_r="残差绝对值";

run;

等级相关系数检验结果见表3。

表3通过SAS软件得到自变量收入与残差绝对值|ei|的相关系数是0.572 18，P值为0.000 8，自变量收入与残差绝对值|ei|显著相关，即存在异方差现象，与残差图的结果吻合。接下来进行white检验，程序如下：

proc reg data=expend2013;

model expend=income / white;

run;

quit;

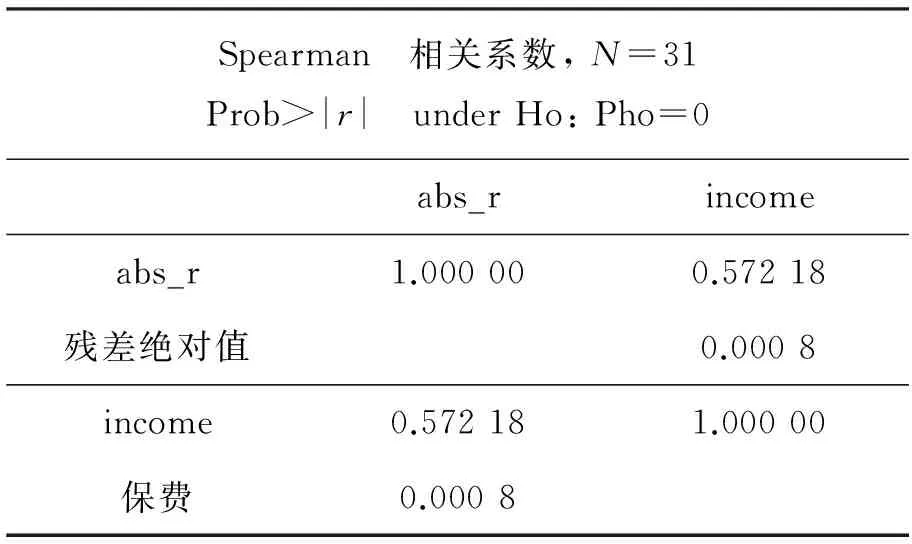
表3　等级相关系数检验结果

white检验结果见表4。

表4　white检验结果

由表4可以判断存在异方差现象(P值<0.000 1)。

下面开始进行加权最小二乘的处理，分别采用残差绝对值和残差平方项作为权重，经比较残差平方项作权重的效果更好。利用残差平方项加权的SAS程序如下：

procregdata=resid;

modelsqresid=income;

outputout=v_weightsp=v_hat;

run;

quit;

datav_weights;

setv_weights;

v_weight=/v_hat;

labelv_weight="weightsusingsquaredresiduals";

run;

procregdata=v_weights;

weightv_weight;

modelexpend=income/noint;

outputout=e2013_r_vr=residual;

labelincome="保费"expend="赔付";

run;

quit;

datar2013_abs_v;

sete2000_r_v;

abs_r_v=abs(residual2);

run;

proccorrdata=r2013_abs_vspearman;

varabs_r_vincome;

run;

加权之后，需要去掉常数项，加权之后的等级相关系数的结果是自变量收入与残差绝对值|ei|的相关系数降为0.243 16，P值为0.111 75，可以判定异方差现象消除了。

表5　加权后的的参数估计结果

图2回归拟合图

5结语

通过SAS软件可以实现残差图法、等级相关系数法、white检验，还可以实现加权最小二乘法消除异方差。SAS软件功能强大，处理异方差的方法的还有很多，SAS软件在这个方面的应用还有待开发。

参考文献：

[1]何晓群.应用回归分析[M].北京:中国人民大学出版社,2011:96-116.

[2]龚秀芳.几种异方差检验方法的比较[J].菏泽师范专科学校学报,2003(25):19-22.

[3]WhiteH.Aheteroskedasticity-consistentcovariancematrixestimatorandadirecttestforheteroskedastivity[J].Econometrica,1980(48):817-838.

[4]杨波.加权最小二乘估计中加权系数的确定[J].现代电子技术,2002(12):45-46.

[5]王纯杰.基于分位数回归的长春市职工工资水平的分析[J].长春工业大学学报:自然科学版,2010,31(4):367-373.

[6]董大钧.SAS统计分析应用[M].北京：电子工业出版社,2008.

[7]朱世武.SAS编程技术教程[M].北京：清华大学出版社,2013.

[8]InstituteS.SAS/STATuser’sguide[M]. [S.l.]:SASInstitute,1990.

Inspection and elimination of heteroscedasticity based on SAS

WANG Chunjie,ZHENG Xi*,LI Qun,LIN Shanyi

(School of Basic Sciences, Changchun University of Technology, Changchun 130012, China)

Abstract：Heteroscedasticity phenomenon is tested with white test of REG procedure in SAS, and the weighted least square estimation is used to eliminate heteroscedasticity. The test is compared with both the residual graph and Spearman correlation coefficient method to show more reasonable results. The data of insurance and premium in 2013 is applied to the example analysis.

Key words：regression analysis; heteroscedasticity; weighted least square estimate.

收稿日期：2016-01-21

基金项目：国家自然科学基金资助项目(11301031，11571051)； 吉林省教育厅“十三五”规划项目(2016317)

作者简介：王纯杰(1978-)，女，汉族，辽宁辽阳人，长春工业大学副教授，博士，主要从事数理统计方向研究,E-mail:wangchunjie@ccut.edu.cn. *通讯作者：郑茜(1989-)，女，汉族，吉林辽源人，长春工业大学硕士研究生，主要从事数理统计方向研究,E-mail:13069008450@163.com.

DOI:10.15923/j.cnki.cn22-1382/t.2016.3.01

中图分类号：O 212.1

文献标志码：A

文章编号：1674-1374(2016)03-0209-08