电磁干扰信号 频谱分析

邵 鄂，张军马，何 越（工业和信息化部电子第五研究所，广州 510610）



电磁干扰信号 频谱分析

邵 鄂，张军马，何 越
（工业和信息化部电子第五研究所，广州 510610）

摘要：在电磁兼容测试过程中，针对某些产品仅因印制板上某些脉冲信号引起辐射骚扰超标导致产品认证失败的问题，首先介绍了与傅里叶变换有关的3个不等式及证明过程，利用这些不等式对不规则脉冲信号的频谱包络进行了详细推导，并用一个具体的不规则脉冲信号进行了频谱包络验证。结果表明：工程上对一些不用精确求取不规则脉冲信号频谱的应用时，利用以上3个不等式即可大大简化频谱包络求取过程，掌握这些脉冲信号的频谱包络特征，对于优化印制板布局、布线具有十分重要的工程指导意义。

关键词：电磁兼容；电磁干扰；脉冲信号；印制板

引言

信号具有时域和频域双重特性，了解常见时域信号的频谱构成十分必要，因为知道了信号的频谱构成，就知道此信号产生电磁干扰的潜在情形。为了抑制电磁干扰，须得考虑信号极端情形，即利用脉冲函数的频谱与傅里叶变换不等式可推导出某些常见时域信号的频谱包络。

求取周期时域信号频谱[1]的常规方法，即通过公式（1）求取傅里叶级数系数ak，即可获得连续时间周期信号的频谱ak。

通过公式（2）傅里叶变换，即可获得非周期时域信号的频谱X(j )w。

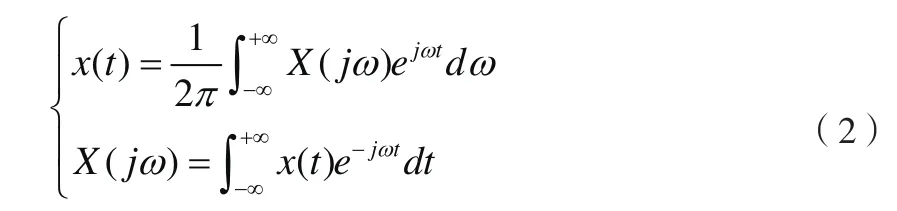
以上两种方法，计算繁琐，并且某些信号的积分很难求出来，对微积分知识要求较高，因此对大多数工程师而言，快速求取时域信号频谱的可操作性不强。事实上，工程师们关注的重点是知道信号的时域特性，如何预估其频谱包络特征，以求在PCB布局、布线时，采取必要的措施减小信号对外的辐射发射或增强PCB的抗电磁干扰的能力。

1 常用不等式及证明

EMC测试故障分析时，经常用到不等式（3）～（5）预估时域信号的频谱。

下面将对不等式（3）～（5）进行详细证明：

其次，结合傅里叶变换对，显而易见得到：

以下对不等式（4）进行证明，首先利用傅里叶变换微分性质：

由（7）式即得到（8）式：

将（7）式展开且同时取模运算，结合（6）式得到（9）式：

结合时域信号傅里叶变换n阶微分性质以及不等式（4）的推导原理，同理可推导出不等式（5），这里不再赘述。

2 频谱包络推导过程

如图1所示，EMC测试不合格原因分析时，常常用示波器监测到类似于图1所示的不规则脉冲信号，其中上升时间为tr，下降时间为tf，脉冲宽度为tp，两峰值幅值为1A和A2。倘若没有频谱仪，仅从时域测试结果，就能方便、快捷预估时域监测信号的频谱，作为电路设计工程师而言尤为重要。利用第1节中的3个不等式，即可快速推导出不规则脉冲信号的频谱包络。

详细推导过程如下：

首先，求取图1所示x( t )信号阴影部分，即不规则四边形的面积，结合第2节中（3）式就得到（10）式：

从（10）式可知，x( t )的频谱幅值应该不大于不规则四边形的面积。一旦x( t )信号的上升时间tr，下降时间tf，脉冲宽度tp，两峰值幅值A1和A2确定了，x( t )的频谱包络就限于阴影部分面积之下了。

其次，为了进一步求取x( t )信号的频谱包络，对x( t )信号做一阶微分得到如图2所示的矩形脉冲波形。然后利用不等式（4）获得x¢( t )信号阴影部分的面积：

另外，由于x( t )信号的二阶微分才为狄拉克冲激函数。因此，要求取x( t )信号的整个频谱包络必须获得x( t )的二阶微分信号。如图3所示，利用傅里叶变换二阶微分性质，结合不等式（5）可求得x¢( t )信号阴影部分的面积：

图1　不规则脉冲信号

图2　不规则脉冲信号一阶导数

图3　不规则四边形信号二阶导数

图4　不规则脉冲信号频谱包络

因此结合不等式（10）～（11）可知，即可获得不规则脉冲信号x( t )的频谱，即频谱包络分为三段，第一段为常数，第二段以20 dB频程下降至f2，第三段以40 dB频程下降至无穷。因此，将X1( f ) ～X3( f )绘制在如图4所示的同一波德图中，只需求出f1和f2即可推导出x( t )的频谱包络。

下面介绍如何求取f1和f2（见图5）：

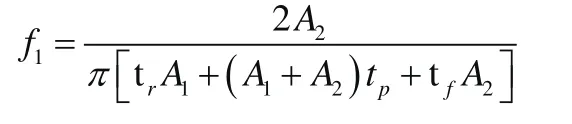
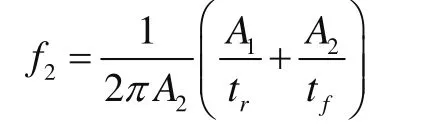
3 不等式应用实例

若不规则脉冲信号x( t )的脉冲幅度A1=1 V，A2=1.2 V，上升时间tr=0.1 us，下降时间tf=0.2 us，脉宽tp=2.35 us，则利用以上结论，即可求得f1和f2，

以下将直接给出f1和f2，的数值，这里不再赘述。

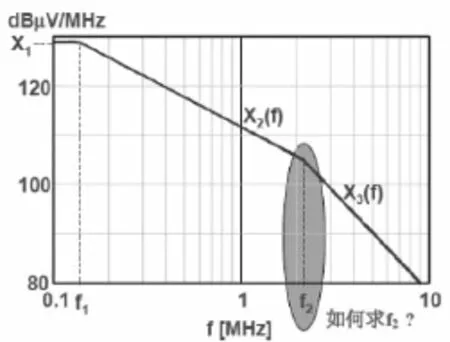
图5　不规则脉冲信号频谱包络

图6　不规则脉冲信号频谱包络

当知道了转折频率f1和f2，频谱幅度和利用不规则脉冲信号频谱的三段式规律，即可绘制出如图6所示的频谱包络。

4 结束语

信号具有时域和频域双重特性，对大部分硬件工程师而言，信号的时域波形较为直观，易于识别与理解；频谱特征却往往难于被接受。然而，工程经验之谈是10 %的电路，常常产生90 %的EMC问题[2]。这10 %的电路往往正是这些不规则的脉冲信号，因此掌握脉冲信号的频谱特征，对印制板布局、布线时如何减小不规则脉冲信号产生的高次谐波导致的传导、辐射骚扰影响具有重要的指导意义。

参考文献：

[1]刘树堂.信号与系统[M]. 2版.西安：西安交通大学出版社, 2007, 6.

[2] Ott, Henry W, 1936-Electromagnetic comtibility engineering [M]. America: Wiley, 2009.

中图分类号：TN601

文献标识码：B

文章编号：1004-7204（2016）02-0034-04

作者简介:

邵鄂（1986.11-），男，毕业于电子科技大学，硕士学位，工程师职称。现任工业和信息化部电子第五研究所质量安全检测中心电磁兼容室工程师，主要从事电磁兼容检测、设计与对策等研究工作。

Spectrum Analysis on Electromagnetic Interference Signal

SHAO E, ZHANG Jun-ma, HE Yue
(CEPREI, Guangzhou 510610)

Abstract：During the EMC test, aiming at the problem that some products can’t pass test owing to some pulse signals which causes excessive radiation disturbance, this paper introduces three inequalities and proof process, which are related to Fourier transform, and then takes advantage of these inequalities to attain spectral envelope of irregular pulse signal. Finally, a specific irregular pulse signal spectral envelope is applied to verify this method. The result shows that some application cases without obtaining accurate irregular pulse signal spectrum, using the above three inequalities can greatly simplify the process of calculating its spectral envelope. It’s a very useful guideline for engineers who master the frequency spectrum characteristics of these pulse signals to handle PCB layout and route.

Key words：EMC; EMI; pulse signal; PCB