基于Kriging模型的载人航天某装置结构优化设计研究

刘 磊，刘洪英，马爱军，冯雪梅，石 蒙，董 睿，赵亚雄（中国航天员科研训练中心，北京 100094）



基于Kriging模型的载人航天某装置结构优化设计研究

刘 磊，刘洪英，马爱军，冯雪梅，石 蒙，董 睿，赵亚雄
（中国航天员科研训练中心，北京 100094）

摘要：对于处在振动环境中的载人航天某装置复杂结构，设计过程中存在最小化质量、同时最大化一阶整体振动频率的多目标优化问题，可以利用多目标遗传算法（NSGA-II）求解得到Pareto最优解集，但利用NSGA-II 进行求解计算量大，对于复杂结构更甚。为了节省计算时间，提出基于Kriging代理模型的复杂结构多目标优化设计方法，首先通过拉丁超立方采样获得样本点，然后通过样本点创建Kriging模型，最后利用多目标遗传算法求解代理模型得到Pareto最优解集，方便设计师从中选择最优解，优化结果表明本文所述方法合理有效。

关键词：载人航天装置；结构优化设计；Kriging模型；拉丁超立方试验设计；多目标遗传算法；Pareto解集

前言

航天器发射过程中要经历复杂的力学环境，比如振动、冲击、失重、辐射等[1]，而振动是需要考虑的重要因素之一[2]。结构的固有频率及固有振型是结构的固有特性，直接体现着结构在振动环境中的振动形式，在航天产品设计中设计师一般希望结构振动频率（特别是低阶频率）能够足够大以远离火箭发射过程中振动频率来避免发生共振造成结构损坏。另一方面，航天产品研制过程中对质量等特性也有着严格的要求，航天器质量每降低1 kg，造价可降低10 000美元[3]，因而航天产品的轻量化设计越来越得到重视[4]。在载人航天某装置研制阶段，设计师希望该装置在满足振动试验条件下重量尽可能的轻，同时希望装置一阶整体振动频率尽可能的大，而结构重量与结构一阶整体振动频率往往存在相互影响制约的关系，因而是个多目标结构优化问题。

针对多目标结构优化问题，可以采用加权变量法求解[5]。为每个目标分配一个权重系数，然而权重系数是人为给定，不同的系数会得到不同的优化结果，经验依赖性强。为了得到结构重量与一阶整体振动频率的Pareto最优解集以方便设计师进行选择，可以通过多目标遗传算法NSGA-II（Non-dominated Sorting Genetic Algorithms-II）[6，7]求解得到。然而，多目标遗传算法求解问题时计算量明显偏大，对复杂结构更甚。为了节省计算时间成本，本文选择采用代理模型的方法，利用NSGA-II求解代理模型以得到该多目标优化问题的Pareto最优解集。所谓代理模型即为计算量小，但计算结果与真实计算程序结果相近的分析模型。代理模型建立有以下步骤[8]：首先通过试验设计获取样本点，然后选择一种代理模型代替上述样本点数据，使两者匹配即可创建代理模型。基于代理模型的结构多目标优化流程如图1所示。

目前常用的代理模型包括径向基函数模型，响应面模型，神经网络模型，Kriging模型等。其中Kriging模型是一种进行曲线插值的方法，是一种估计方差最小的无偏估计模型[9]，可以利用较少样本点拟合非常复杂的形状，适合设计变量较多的优化问题，因而本文采用Kriging模型代替复杂有限元分析模型来进行复杂结构的多目标优化设计研究。

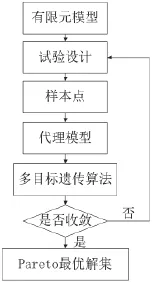
图1　基于代理模型的结构多目标优化流程图

1 Kriging 模型原理

Kriging 作为线性回归分析的一种改进的技术，包含了线性回归部分和非参数部分，其中非参数部分被视作随机过程的实现。假设随机过程服从高斯分布, 其中协方差矩阵的系数可以通过极大似然估计确定[10]。Kriging模型包含回归部分和非参数部分。

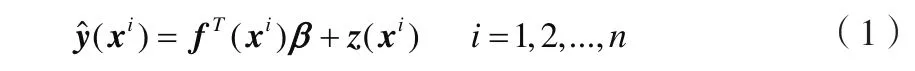
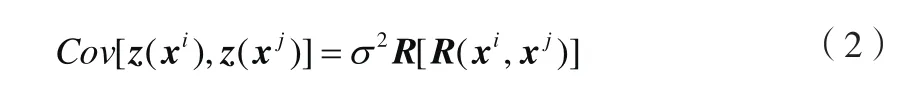
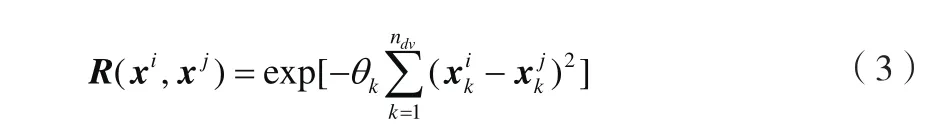
则任意试验点xi的响应估计为

式中：rT( x )为长度ns的试验点x与采样点{x1, x2, ..., xns}间的相关向量，可以由下式（5）确定

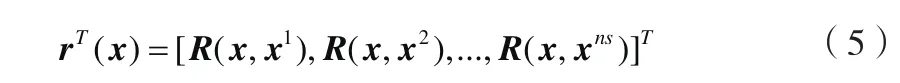
而全局模型方差的估计值为

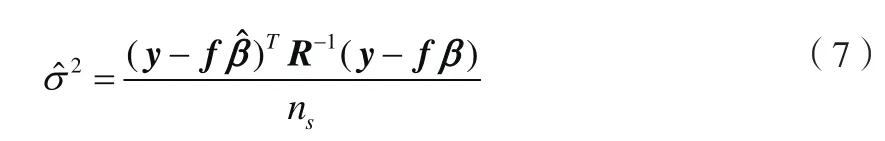
通过极大似然估计确定相关函数矩阵的参数，可以得到下式（8）最优化问题，来确定参数θk。

当θk求出，代入式（3）求得R(xi,xj)，然后代入式（5）可得到未知点x与已知数据样本的相关向量rT(x)，然后代入式（4）得到其响应值，进行Kriging模型的创建。

2 某载人航天装置结构多目标优化设计

2.1 问题描述

正在研制的某载人航天装置结构复杂，为外部框架与内部多个功能单机产品组成。外部框架由梁、板构成，因此有限元建模时选择二维面网格进行划分，而内部单机产品根据其结构不同特点合理选择面网格、体网格进行划分。为了保证优化结果的可信性，根据文献[11]中提供的有限元建模修正方法，利用试验件的实验结果对装置初始有限元模型进行修正，图2为修正过的装置有限元模型。

对该产品进行模态分析得到结构前两阶振型为顶板的局部振动，第三阶为结构的一阶整体振动，大小为58.20 Hz。装置一阶整体振动振型如图3所示。

由于该装置内部单机为功能产品，内部构造及安装位置都不能进行改变，而外部框架由于装船位置相对固定，也不宜进行拓扑方式的调整，因而设计变量选定为部分可调整框架梁的厚度尺寸，设计变量的确定基于以下原则。

1）根据设计方要求选择厚度可调整梁，并将厚度相同、功能相似的梁归并为一类，以保证优化后这些梁厚度尺寸仍相同，以便于生产加工。

图2　装置有限元模型

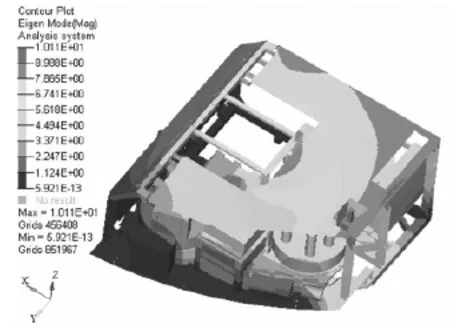
图3　装置一阶整体振动振型图

表1　设计变量初始值、上下限

2）为保证尺寸调整不影响其他功能的实现，选择对框架梁厚度尺寸在初始设计尺寸下进行微调，根据一定原则对每个尺寸分别设置上下限。

初步分析得到框架可调厚度尺寸有10个，表1为设计变量初始值以及上下限。该优化问题可表示为式（9）的数学模型式，其中优化目标有两个，一是最小化设计域结构质量（用Mass表示，下同），另一个是最大化结构一阶整体振动频率（用Frequency表示，下同）。

2.2 试验设计

DOE ( Design Of Experiment)-试验设计，是用来研究输入变量对一个或多个输出响应影响的一种统计方法[12]。试验设计是基于最优化思想，通过广义试验进行最优设计的一种优化方法。试验设计从不同的优良性出发，通过合理设计试验方案，能够有效控制试验干扰，达到科学处理试验数据，全面进行优化分析以实现优化的目标，已成为现在结构优化设计技术的一个重要方面。

目前常用试验设计方法包括正交试验设计、均匀试验设计、拉丁超立方设计等。其中。拉丁超立方设计是一种修正的蒙特卡罗方法，适用于影响因素较多的情况，被证明用于创建Kriging模型效果较好[13]。本文首先采用拉丁超立方试验设计对设计变量进行采样，然后代入有限元模型计算求解获得输出响应值，共得到66个样本点，并基于样本点进行以下研究：①确定哪些输入变量对输出响应影响最大。②用以构建Kriging代理模型来代替计算量非常大的实际模型进行求解。

根据对拉丁超立方采样得到的66个样本点进行分析，可以得出设计变量对输出响应的影响程度。图4是响应与设计变量插值函数关系，可以看出设计变量dv1对质量和频率响应影响都是最大。

2.3 Kriging代理模型的建立

本文利用拉丁超立方采样获得的样本点，创建Kriging代理模型，然后对该代理模型的可信度进行评估。代理模型的可信度是由额外的试验点来验证，这些验证点是由某种试验设计方法生成的新设计样本点，而不是上述生成代理模型的样本点，这样能够较好的检验代理模型的精度。

Kriging代理模型的精度可以利用以下公式（10）来验证：

其中拉丁超立方设计共产生66个样本点用于创建Kriging模型，而利用部分因子设计产生另外16个样本点用于对Kriging的可信度进行评估。计算结果显示，对于质量响应，R2=1，是由于质量响应与设计变量之间为简单的线性关系，而对于频率响应，R2=0.997，同样接近于1，表明利用Kriging模型代替原有有限元计算模型可信度很高。

2.4 多目标遗传算法优化

在代理模型基础上，利用多目标遗传算法完成此优化设计问题。遗传算法是模拟自然选择与遗传的随机搜索算法，是用于求解全局优化最流行的一种算法，而改进的非支配排序遗传算法NSGA-II可以用于解决多目标优化问题，其可以提供一系列的帕累托解，而非单一解。该优化设计过程基于多学科优化平台HyperStudy[14]进行，设置最大迭代次数100，其余参数取默认值，可以得到优化后Pareto曲线如图5所示。

图4　响应与设计变量的线性插值关系

图5　多目标优化Pareto最优解集

设计师可以根据Pareto最优解集并按照实际需求选择最合适方案，如若保持一阶整体振动频率58.20 Hz不变，设计域最小质量为12.94 kg，可比原设计降低0.79 kg（原设计为13.73 kg），优化减重5.8 %，表明原设计存在优化空间。表2为优化后经过圆整的结构尺寸。

为了进一步研究Kriging模型代替原有结构有限元模型的有效性，将优化后结构尺寸带入有限元模型进行计算，表3为Kriging模型结果与有限元计算结果的比较，表中数据显示两个结果基本相同，误差极小，表明Kriging模型求解该优化问题合理有效。最后对优化后结构进行振动试验条件下的力学特性分析以校核应力，结果表明应力有很大余量，满足要求。

表2　设计变量优化解

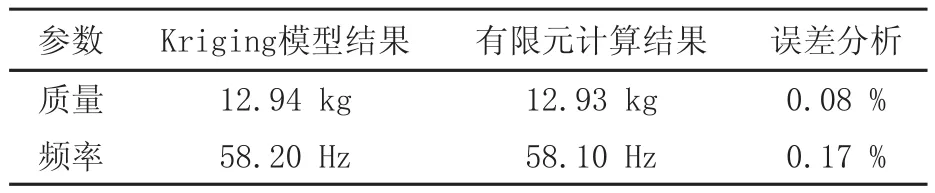
表3　Kriging模型结果与有限元计算结果比较

3 结论

本文针对利用多目标遗传算法求解复杂结构计算量过大的问题，提出基于Kriging代理模型的多目标优化流程，并对载人航天某装置进行多目标优化设计研究，得到该结构质量与一阶整体振动频率的Pareto最优解集，设计师从中选择最适合该产品的最优解。结果表明该方法在大大减少计算时间的同时保留着极高的精度，而优化后结构在一阶整体振动频率保持不变的情况下质量有一定幅度的下降，取得很好的优化效果，表明本文所提方法的合理有效性，可以为同类产品优化设计提供参考。

参考文献：

[1]刘洪英, 马爱军, 安梅岩, 等. 冲击响应谱规范试验室模拟述评[J].环境技术, 2010, 30(5): 34-37.

[2]马兴瑞, 于登云, 韩增尧, 等. 星箭力学环境分析与试验技术研究进展[J]. 宇航学报, 2006, 27(3): 323-331.

[3]Tibert G. Deployable tensegrity structures for space applications [D]. Stockholm: Royal Institute of Technology, 2002.

[4]邱吉宝, 王建民, 谭志勇, 等. 航天器结构动态优化设计仿真技术[J]. 强度与环境, 2003, 30(2): 6-16.

[5]刘远东, 尹益辉, 郭中泽. 考虑静动力学特性的材料/结构一体化多目标优化设计[J]. 工程力学, 2012, 29(9): 37-41.

[6]Deb K，Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6 (2): 182-197.

[7]Srinivars N, Deb K. Multi-objective function optimization using non-dominated sorting genetic algorithms [J]. Evolutionary Computation, 1995, 2(3): 154-157.

[8]Simpson T W, Mauery T M, korte J J. Kriging models for global approximation in simulation-based multidisciplinary design optimization [J]. AIAA journal,2001, 39(12): 2233-2241.

[9]张维刚, 刘晖. Kriging模型与优化算法在汽车乘员约束系统仿真优化中的应用研究[J]. 湖南大学学报（自然科学版), 2008, 6: 23-26.

[10]张崎, 李兴斯. 基于Kriging模型的结构可靠性分析[J]. 计算力学学报, 2006, 23(2): 175-179.

[11]张令弥. 动态有限元模型修正技术及其在航空航天结构中的应用[J]. 强度与环境, 1994 (2): 10-17.

[12]刘克龙, 姚卫星, 穆雪峰. 基于Kriging代理模型的结构形状优化方法研究[J]. 计算力学学报，2006, 23(3): 344-347.

[13]Simson T W. A concept exploration method for product family design [D]. Atlanta: Georgia Institute of Technology, 1998.

[14]洪清泉, 赵康, 张攀, 等. Optistruct & HyperStudy 理论基础与工程应用 [M]. 北京: 机械工业出版社, 2013.

中图分类号：V414.19

文献标识码：A

文章编号：1004-7204（2016）02-0055-05

基金项目：中国载人航天工程基金项目

作者简介:

刘磊（1991-），男，硕士，研究方向：航天振动、冲击环境条件下结构优化设计。

马爱军（1969-），男，博士，研究员，研究方向：航天振动、冲击环境模拟试验技术。

Study on Structural Optimization of a Manned Aerospace Assembly Based on Kriging Model

LIU Lei, LIU Hong-ying, MA Ai-jun, FENG Xue-mei, SHI Meng, DONG Rui, ZHAO Ya-xiong
（China Astronaut Research and Training Center, Beijing 100094）

Abstract：For a manned aerospace assembly under vibration environment, there are two objectives in design phase: min mass and max first integral vibration frequency. Usually it can be solved by using multi-objective genetic algorithm (NSGA-II), but the computing amount is too large, especially for complex structure. To drop the computing time of using of NSGA-II in multi-objective structural optimization, a method based on Kriging model was proposed. The method achieved the samples from Latin hypercube design firstly and created the Kriging model based on the samples. Then multi-objective optimization problem could be solved using NSGA-II on the Kriging model and got the Pareto set finally. The results verify the effectiveness and practicability of the method.

Key words：manned aerospace assembly; structural optimization design; Kriging model; Latin hypercube design; multi-objective genetic algorithm; Pareto set