框架型人工鱼礁布放过程的动力学分析
2016-07-18隋吉盛郑中强常宗瑜于振江
隋吉盛, 郑中强, 常宗瑜,2, 于振江
(1 中国海洋大学工程学院,山东 青岛,266100;2 山东省海洋工程重点实验室,山东 青岛,266100)
框架型人工鱼礁布放过程的动力学分析
隋吉盛1, 郑中强1, 常宗瑜1,2, 于振江1
(1 中国海洋大学工程学院,山东 青岛,266100;2 山东省海洋工程重点实验室,山东 青岛,266100)
摘要:为解决不当的人工鱼礁布放操作导致的鱼礁碰撞破坏、布置点偏离目标地点过大等问题,对静水环境下框架型人工鱼礁布放的动力学过程进行了研究。基于人工鱼礁下落过程的水动力学模型、鱼礁与海底接触碰撞模型,对现有碰撞力公式进行合理修正,建立了人工鱼礁布放过程的整体动力学方程;采用数值方法对动力学方程进行求解,得到鱼礁下落速度以及不同海底底质条件下的着底冲击力。分析表明,海底底质越硬,着底冲击力越大。采用多体动力学软件ADAMS对鱼礁在不同初始姿态下的布放过程进行模拟,采用有限元软件ANSYS Workbench对鱼礁结构进行强度分析。结果表明,鱼礁初始姿态倾斜角度越大,下落达到的稳定速度越小;棱着底的最大冲击力比面着底的要小,但产生的应力更大;最大应力发生在着底棱的中部。本研究可为合理规划人工鱼礁的布放和人工鱼礁的设计提供参考。
关键词:人工鱼礁;布放;动力学;模拟
人工鱼礁是海洋牧场建设的重要组成部分,鱼礁沉设在海底,产生饵料效应、流场效应等,能够诱集鱼类,保护和增殖渔业资源[1-2]。当前人工鱼礁的研究方向主要集中在生物技术、礁体设计以及流场效应等方面[3-6],对人工鱼礁布放过程的研究甚少。不当的人工鱼礁布放操作会产生鱼礁碰撞受到破坏、布置点偏离目标地点过大等问题。一般应用较多的投放方法是从船台投下或把鱼礁吊起送到水面后脱钩投放[7]。投放地点最好为硬质海底,水深一般在10~60 m,流速以不超过0.77 m/s为宜[8-9]。
在人工鱼礁布放理论研究方面,中村充[10]提出人工鱼礁下落速度和着底冲击力的计算公式,但未考虑海底基底的阻尼效应;松见吉晴等[11-12]分析了人工鱼礁的投放姿态对下落姿态和着底冲击力的影响;王磊等[13]对船形鱼礁的沉降过程进行了分析计算,得出船形鱼礁的下落速度、时间。在人工鱼礁布放实验方面,铃木达雄[14]对人工鱼礁投放后的分散情况进行了实验研究,发现水深越深,分散程度越大;刘同渝等[15]发现冲击力与礁体的相对密度有关,即相对密度越小,冲击力越小;Huang[16]认为海底底质为岩石时的冲击力是鱼礁自重的9.7倍,而沙质海底时的冲击力为鱼礁自重的3.7倍;秀岛好昭等[17]通过角型鱼礁的碰撞实验提出了鱼礁冲击时应力的计算方法。在人工鱼礁布放数值模拟研究方面,Sol Han等[18]用ANSYS CFX软件计算鱼礁下落的速度、位移和动能。
本文对静水环境下人工鱼礁布放过程进行了动力学研究,在相关研究[10]的基础上,对人工鱼礁布放过程的动力学方程进行了修正,采用数值积分方法进行求解;采用多体动力学软件ADAMS 模拟鱼礁布放的整个过程,并采用有限元软件ANSYS Workbench对鱼礁结构进行强度分析,为人工鱼礁的布放和设计提供参考。
1人工鱼礁布放过程的动力学分析
小型混凝土框架型人工鱼礁因其结构简单、工作性能优良、制造成本低而被广泛使用[19]。以某混凝土框架型人工鱼礁为例,对其布放过程进行了研究。框架型人工鱼礁三维模型如图1所示,其参数与数值分别为:鱼礁外形尺寸为2 m×2 m×2 m,每个面挖空尺寸为1.6 m×1.6 m,密度σ为2 500 kg/m3,体积V为0.832 m3,鱼礁迎水面的面积A为1.44 m2。
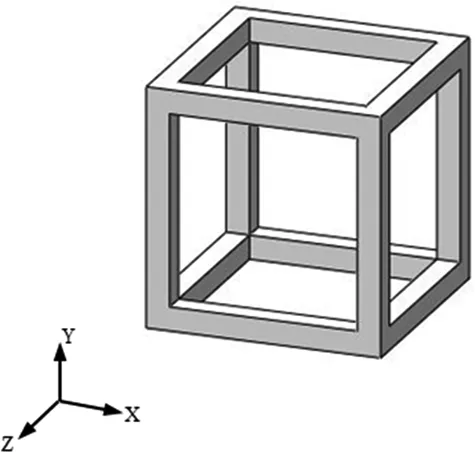
图1 框架型人工鱼礁三维模型Fig.1 Three-dimensional model of a frame-type artificial reef
1.1人工鱼礁下落过程中的受力分析
鱼礁投放后在海水中下落过程受到的力包括重力、浮力、水动力和鱼礁与海底产生的碰撞力。鱼礁所受到的水动力可以根据Morison方程计算[19]:

(1)
式中:u—鱼礁下落速度,m/s;ρ—海水密度,kg/m3;V—鱼礁体积,m3;CD—鱼礁阻力系数,此处取2.0;A—鱼礁迎水面的面积,m2;CMA—鱼礁附加质量系数,此处取1.0。
参照Gobat[20]将海底基底简化为具有线弹性系数及阻尼的物理模型,对人工鱼礁触底时的碰撞力公式[10]进行修正:
(2)
式中:KR—海底基底反力弹性系数,kg/m2;ε—海底基底的变形,m;c—阻尼系数,Ns/m。根据鱼礁的落下实验,落向地盘时,n=2。关于KR值,沙砾底质时,KR=1.6~5.0×106kg/m2;坚硬密实的黏土底质时,KR=2.1~6.3×106kg/m2。
因此可以得到人工鱼礁布放过程的整体动力学方程:
(3)
人工鱼礁在接触海底之前不受碰撞力,此时δ1=1,δ2=0;当人工鱼礁接触海底时,可以认为迎水面不受水动力作用,只有碰撞力R作用在礁体上,所以δ1=0,δ2=1。
1.2人工鱼礁在触底前的运动分析
鱼礁投放后在海水中下落的运动方程可由式(3)整理得:
(4)
利用数值积分方法对方程式(4)进行求解,得到鱼礁触底前下落过程的运动响应(图2)。
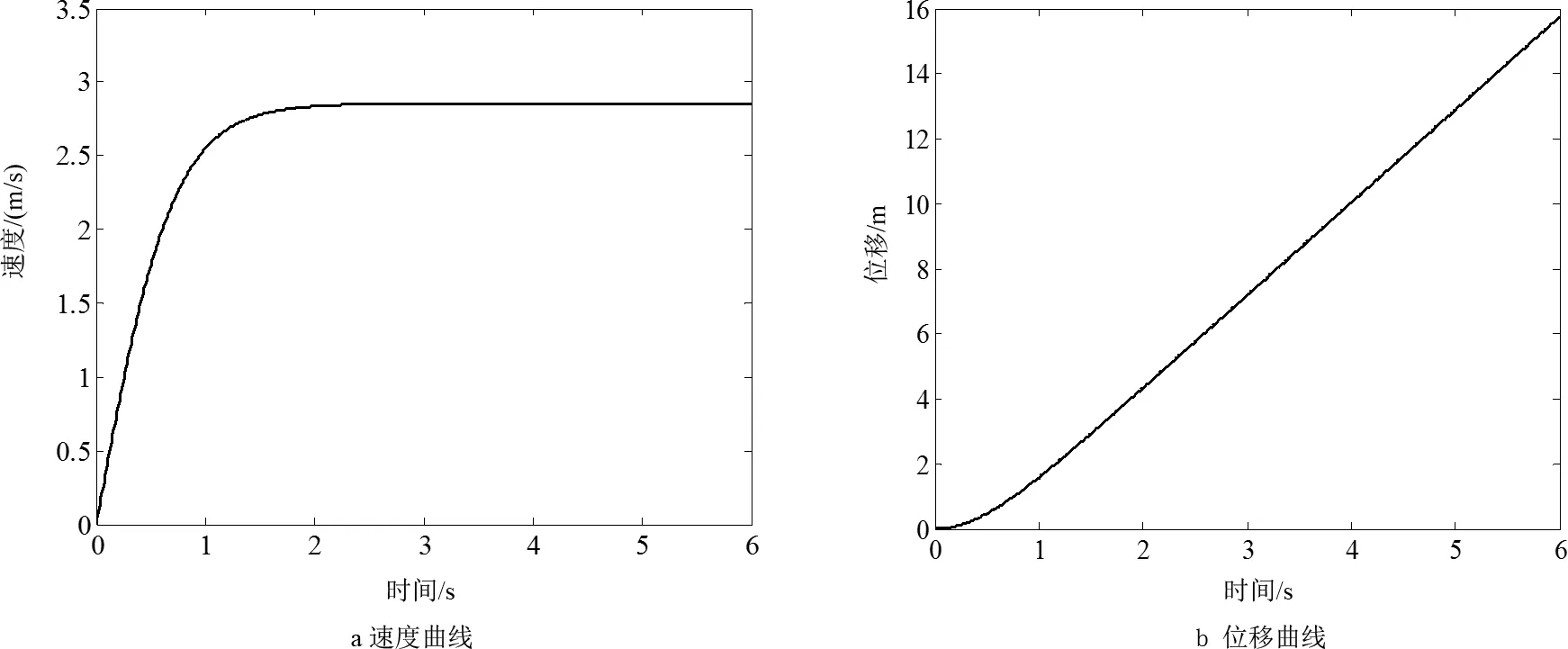
图2 人工鱼礁触底前的下落运动响应Fig.2 Motion responses of the falling artificial reef before touching the seabed
图2a、2b分别是鱼礁下落过程的速度和位移曲线。从图中可以看出,鱼礁在下落1.8 s之前,重力起主要作用,鱼礁下落速度增加较快;随着速度的增加,水阻力增大,鱼礁的加速度变小,直到水阻力与鱼礁在水中的重量相等时,下落速度变为稳定速度uc;当下落2.5 s时,达到稳定速度2.854 5 m/s,此时鱼礁下落位移约为6 m。人工鱼礁的设置水深一般都在10 m以上,对本框架型人工鱼礁而言触底前会达到稳定速度。
(5)
从而求得稳定速度为:
(6)
其结果与数值积分计算结果一致。
1.3人工鱼礁触底时的运动分析
如果鱼礁底面着底,接触面之间被认为没有水存在,可以忽略水动力阻力项和惯性力项,即δ1=0,δ2=1。

(7)
利用数值积分方法对方程式(7)进行求解,得到不同海底底质下的海底基底变形和着底冲击力曲线(图3、图4)。
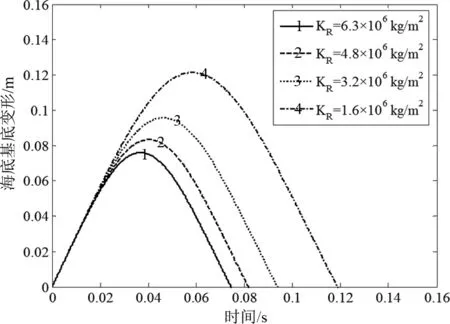
图3 不同海底底质下的海底基底变形曲线Fig.3 Seabed deformation with different
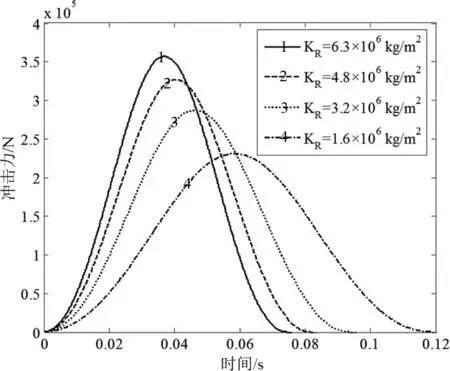
图4 不同海底底质下的着底冲击力曲线Fig.4 Landing impact force with different
从图3、图4可以看出,海底基底反力弹性系数KR值越大,即海底底质越硬,则碰撞作用时间越短,碰撞时海底基底变形量越小,最大着底冲击力越大。由于实际测量鱼礁投放海域海底基底反力弹性系数的成本较大,以及出于安全性因素考虑,理论分析阶段宜采用KR值较大情况进行计算。因此,本文将对KR取6.3×106kg/m2进行研究。
KR取6.3×106kg/m2时,鱼礁与海底基底的碰撞作用时间约为0.074 s。由于着底冲击力的计算结果并不是一个收敛的曲线,因此只在碰撞时间段内求解,而忽略弹起后的时间段。随着鱼礁碰撞海底基底,鱼礁的下落速度不断减小,在0.036 4 s时,鱼礁的下落速度达到临界值0,此时海底基底变形达到最大值0.075 m,着底冲击力也达到最大值3.561×105N。
2人工鱼礁布放过程的动力学模拟
将人工鱼礁的三维模型导入多体动力学分析软件ADAMS中,根据式(1)、式(2)施加载荷及边界条件,进行布放过程的动力学模拟(图5)。
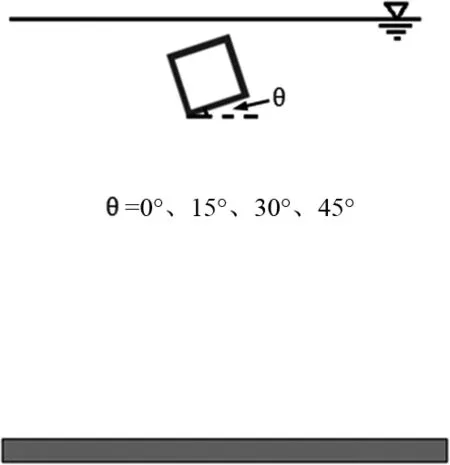
图5 不同初始姿态的人工鱼礁在ADAMS软件中分析环境示意图Fig.5 Analysis situation of the artificial reef in differentinitial postures based on ADAMS software
在实际布放过程中,人工鱼礁下落过程除受重力、水动力外,还受浪、流以及人为因素的影响较大,其下落的姿态会出现倾斜,着底部位也由面着底变为棱着底,甚至是点着底,下落速度与着底冲击力也会有所不同。本文对人工鱼礁不同初始姿态的布放过程进行了动力学模拟,其初始姿态分别为底面与水平面成0°、15°、30°、45°倾角,得到人工鱼礁下落速度和着底冲击力曲线(图6、图7)。

图6 不同初始姿态速度曲线Fig.6 Velocity in different initial postures

图7 不同初始姿态布放着底冲击力曲线Fig.7 Impact force in different initial postures
从速度曲线可以看出,面着底(即0°)时鱼礁下落的稳定速度为2.854 5 m/s。鱼礁在与海底基底接触时速度会瞬间减小,随后逐渐趋于0,达到静止状态。鱼礁与海底基底的初次碰撞冲击力比鱼礁弹起后再下落的冲击力大得多,因此对初次碰撞冲击力曲线进行分析。从图7可以得出,最大冲击力为3.071×105N。碰撞作用时间为0.076 s,对应鱼礁的位移曲线可以得到海底基底的最大变形为 0.071 m。对比动力学模拟的结果和动力学方程的理论解,下落速度一致,海底基底变形偏小0.004 m,偏小5.33%;最大冲击力偏小0.49×105N,偏小13.76%,结果与动力学方程的理论解比较吻合。
初始姿态倾斜下落,鱼礁着底时的姿态由面着底变为棱着底,着底姿态不稳定,需要较长的时间才能达到稳定状态。随着鱼礁倾斜角度的增加,鱼礁迎水的投影面积增加,所受水动力阻力增大,鱼礁下落的稳定速度变小,冲击力相比面着底大幅减小。冲击力大小不仅与稳定速度有关,还与碰撞角度有关,变化规律较为复杂。虽然棱着底时冲击力变小,但碰撞接触由面接触变为线接触,接触面积大幅减小,鱼礁所受应力更大,对鱼礁的结构强度提出了更高的要求。
3人工鱼礁强度分析
根据动力学模拟得到的最大冲击力,在有限元软件ANSYS Workbench中对鱼礁结构进行强度分析。设置鱼礁顶面(边)约束,分别对底面和着底棱施加最大冲击力,得到鱼礁在各倾斜角度下的应力(图8)。
从应力图上可以看出,在鱼礁棱的交点处会出现应力集中,所以在设计鱼礁时尽量在棱交点处使用倒角。除去上述应力奇异值后,面着底时鱼礁所受最大应力发生在底面棱的中部,最大值约为10 MPa;棱着底时鱼礁所受最大应力发生在着底棱的中部,随着倾斜角度的增加,鱼礁所受最大应力增大,倾斜45°时的最大应力约为25 MPa。根据危险截面上的最大应力及鱼礁材料的许用应力即可进行强度检验。棱着底相比面着底,产生的应力更大,更容易发生破坏,在鱼礁设计时可以考虑对着底棱进行加固处理。

图8 人工鱼礁在不同倾角时的应力Fig.8 Von-Mises stress of the artificial reef at different angles
4结论
对框架型人工鱼礁布放过程进行动力学研究。对不同海底底质下鱼礁的着底冲击力分析表明,海底底质越硬,着底冲击力越大;对不同初始姿态的鱼礁投放分析表明,初始姿态倾斜角度越大,下落达到的稳定速度越小;棱着底的最大冲击力比面着底的要小,但达到稳定姿态所需的时间要延长。对鱼礁结构强度分析表明,最大应力发生在着底棱的中部;虽然棱着底的最大冲击力比面着底的要小,但产生的应力更大,对鱼礁的结构强度要求更高,在鱼礁设计时可以考虑对着底棱进行加固处理。
□
参考文献
[1]刘同渝.国内外人工鱼礁建设状况[J].渔业现代化,2003(2):36-37.
[2]杨吝,刘同渝,黄汝堪.中国人工鱼礁的理论与实践[M].广州:广东科技出版社,2005:54-77.
[3]BAINE M. Artificial reefs:a review of their design, application, management and performance[J]. Ocean Coastal Management, 2001, 44(3):241-259.
[4]SHERMAN R L, GILLIAM D S, SPIELER R E. Artificial reef design:void space, complexity, and attractants[J]. ICES Journal of Marine Science, 2002, 59:196-200.
[5]林军,章守宇.人工鱼礁物理稳定性及其生态效应的研究进展[J].海洋渔业,2006,28(3):258-262.
[6]JIANG Z, LIANG Z, HUANG L,etal. Characteristics from a hydrodynamic model of a trapezoidal artificial reef[J]. Chinese Journal of Oceanology and Limnology, 2014, 32:1329-1338.
[7]夏章英,卢伙胜,冯波,等.人工鱼礁工程学[M].北京:海洋出版社,2011:107-108.
[8]李文涛,张秀梅.关于人工鱼礁礁址选择的探讨[J].现代渔业信息,2003,18(5):3-6.
[9]赵海涛,张亦飞,郝春玲,等.人工鱼礁的投放区选址和礁体设计[J].海洋学研究,2006,24(4):72-74.
[10]中村充,上北征男.人工魚礁の着底衝撃力に関する研究——水中落体の着底衝撃力の解析[J].Bulletin of the National Research Institute of Agricultural Engineering,1977(16):111-122.
[11]松見吉晴,横山忠弘,瀬山明.海上投入法による魚礁の安定配置に関する研究[J].PROCEEDINGS OF COASTAL ENGINEERING,1988,35:747-751.
[12]松見吉晴, 横山忠雄.漁礁沈設時の着底衝撃力に関する研究[R].鳥取:鳥取大学工学部,1989.
[13]王磊,唐衍力,陈晓蕾,等.混凝土船形鱼礁的礁体设计与沉降计算[J].中国海洋大学学报,2010,40(7):43-46.
[14]鈴木達雄.投入式ブロックの散乱制御に関する実験[J].水産工学,2013,50(2):119-124.
[15]刘同渝,吴迪,敖卓运.人工鱼礁论文报告集[R]//广州:全国人工鱼礁技术协作组,1987:36-42.
[16]HUANG C C. The study of the impact load of artificial reefs during placement[R]. Taiwan:Proceedings, 16th Conference on Ocean Engineering, 1994:67-78.
[17]秀島好昭,上北征男.人工魚礁の着底衝撃力に関する研究-2-岩盤·コンクリ-ト基盤での着底[J].Bulletin of National Research Institute of Fisheries Engineering,1983(4):59-71.
[18]SOL HAN, DONGHA KIM, QUYNH TN LE,etal. Characteristics of artificial reefs in installation stages[C]//Incheon:The 2015 World Congress on Advances in Civil, Environmental, and Materials Research (ACEM15), 2015.
[19]KIM D, HAN S, LE Q T N,etal. Flow characteristics of unit artificial reefs in 3-D placement models[C]//Incheon:The 2015 World Congress on Advances in Civil, Environmental, and Materials Research (ACEM15), 2015.
[20]王树青,梁丙辰.海洋工程波浪力学[M].青岛:中国海洋大学出版社,2013:139-141.
[21]GOBAT J I, GROSENBAUGH M A. Time-domain numerical simulation of ocean cable structures[J]. Ocean Engineering, 2006, 33(10):1373-1400.
Dynamics analysis on the deployment of a frame-type artificial reef
SUI Jisheng1, ZHENG Zhongqiang1, CHANG Zongyu1,2, YU Zhenjiang1
(1EngineeringCollege,OceanUniversityofChina,Qingdao266100,China;2ShandongProvinceKeyLaboratoryofOceanEngineering,Qingdao266100,China)
Abstract:Improper operation during the deployment of artificial reefs (ARs) can result in some problems, such as collision damage, drop site faraway from target spot, etc.. In this paper, the deployment process of a frame-type ARs in still water environment is studied. Based on the hydrodynamic model during subsidence and the colliding model between the ARs and seabed, the existing impact force formula is amended, and the overall motion equations are developed. The numerical method is used to solve the ordinary differential equations to obtain the velocity and the impact force with different seabed stiffness. The results show that the impact force increases with the increase of stiffness. The multi-body dynamics software ADAMS is used to simulate the deployment process of the ARs in different initial postures, and the strength analysis is carried out based on the finite element software ANSYS Workbench. The results show that the larger the initial angle is, the smaller the steady falling velocity is achieved; when an edge collides with the seabed the maximum impact force reduces compared to a surface, but it produces greater stress; and the maximum stress occurs in the middle of the colliding edges. This work can be a reference for the scientific design and deployment planning of artificial reefs.
Key words:artificial reefs(ARs); deployment; dynamics; simulation
DOI:10.3969/j.issn.1007-9580.2016.03.014
收稿日期:2016-02-27修回日期:2016-05-19
基金项目:山东省自然科学基金项目(ZR2010EM052);青岛市博士后人员应用研究项目(861605040097);中央高校基本科研业务费专项资金(841513053)
作者简介:隋吉盛(1991—),男,硕士研究生,研究方向:海洋装备动力学。E-mail:suijisheng66@163.com 通信作者:常宗瑜(1973—),男,教授,博导,研究方向:海洋装备动力学与控制。E-mail:zongyuchang@ouc.edu.cn
中图分类号:S953.1
文献标志码:A
文章编号:1007-9580(2016)03-074-06
