利用三星时频差的运动辐射源定位与测速方法*

张宇阳

(中国西南电子技术研究所，成都 610036)



利用三星时频差的运动辐射源定位与测速方法*

张宇阳**

(中国西南电子技术研究所，成都 610036)

摘要：针对高轨三星无源定位系统对空中恒定高度运动目标探测的应用场景，提出了一种利用信号到达时差(TDOA)、到达频率差(FDOA)的无源定位与测速方法。详细描述了算法原理、算法处理步骤，利用STK(Satellite Tool Kit)软件结合计算机仿真，分析了时差测量误差、频差测量误差、高程估计误差对定位精度与测速精度的影响。该方法定位精度与测速精度较高，具有一定的工程应用价值。

关键词：三星无源定位；运动辐射源；测速；到达时间差；到达频率差

高轨卫星平台对地观测范围大，具有较强的信号侦收和截获能力，对非合作辐射源进行位置估计是卫星平台非合作信号处理的重要功能之一，其主要方法有测频定位[1-2]、测向定位[3]、双星时频差定位[4-5]、三星时差定位[6]。目前对无源定位的研究主要集中在对地球表面静止目标进行定位，对具有一定高程的运动目标进行定位分析较少。本文利用3颗卫星截获到信号并计算信号间的时差和频差信息，构建定位与测速方程，解算获得信号位置和速度。该方法通过对其卫星通信上行信号或雷达信号100 ms的短时观测，实现对信号的定位与测速。

1辐射源定位与测速原理

三星时频差定位与测速原理如图1所示，利用同一辐射源信号到达主星与辅星A的时间差Δt1和到达主星与辅星B的时间差Δt2，在地球面投影的两组双曲线交点确定辐射源的位置，如图2所示。

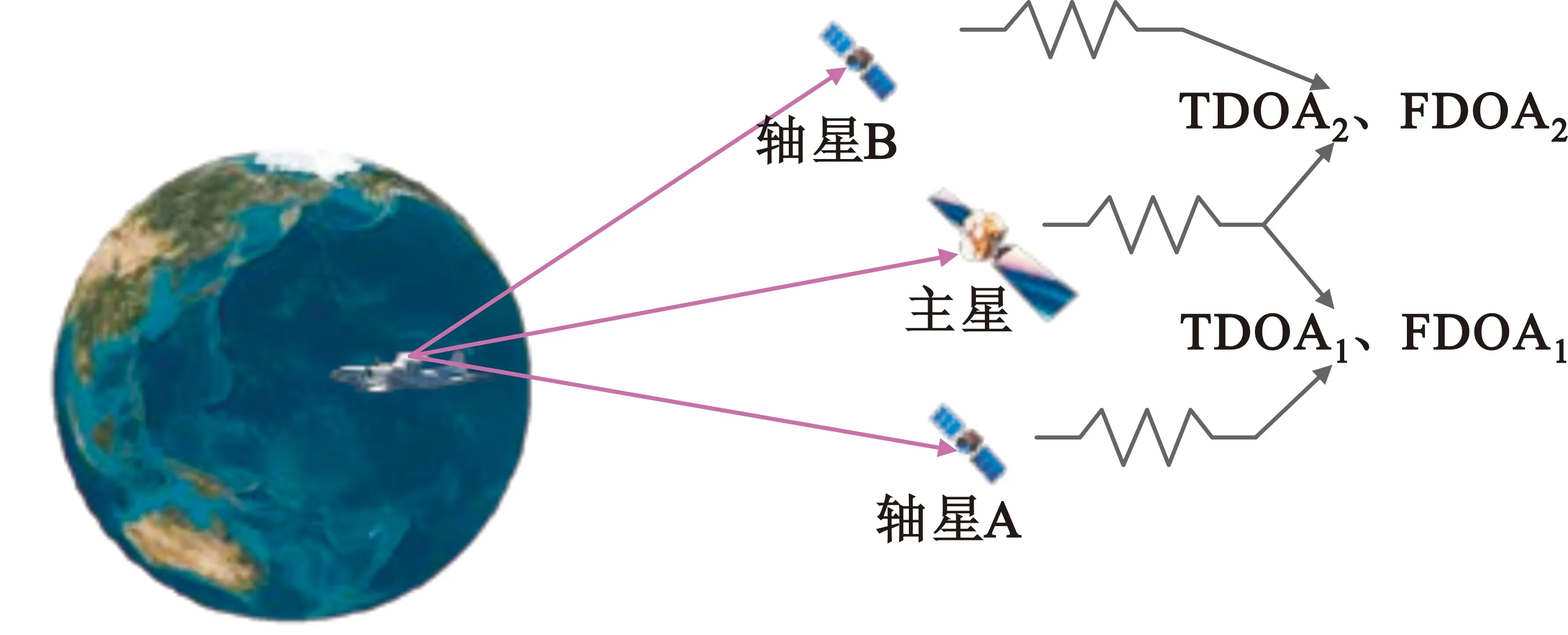
图1　三星定位与测速原理

(a)与辐星A的等时差线

(b) 与辐星B的等时差线

设在地固坐标系中，辐射源坐标为u=[x,y,z]T，速度为v=[vx,vy,vz]T，3颗观测卫星的位置矢量分别记为s1=[x1,y1,z1]T，s2=[x2,y2,z2]T，s3=[x3,y3,z3]T，速度矢量为vs1=[vx1,vy1,vz1]T,vs2=[vx2,vy2,vz2]T,vs3=[vx3,vy3,vz3]T，则Δt1、Δt2与卫星位置、辐射源位置的关系可以确定如下时差定位方程:

(1)

式中：c为光速；R为目标距地心的距离；e为地球偏心率。解此方程可获得辐射源位置。

辐射源速度与观测卫星位置、速度、辐射源频率及信号达到频差的关系如下面的频差方程所示：

(2)

式中：fc为辐射源信号频率；Δf1、Δf2分别为辐射源到达主星与辅星A和辅星B的频率差。上述观测方程中有3个未知数，但观测方程只有两个，存在非唯一解。针对空中匀速巡航目标，可假设目标在与地球面平行的曲面上飞行，即在经度和纬度方向上的速度为vL和vB，高程方向速度为0，并通过坐标变换将vL和vB转换成地固坐标系下XYZ方向的速度分量并代入频差方程，这样频差方程中仅有两个未知数，即vL和vB，通过求解频差方程就可得目标辐射源的速度。

时频差的测量可以用模糊函数法，有兴趣的读者可参见文献[7-8]。

2算法描述

2.1定位处理算法

在实际应用中，对于空中辐射源，具有一定的飞行高度，时差方程中的第三个方程，其中R的取值不能再取为地球长轴长a，而应为长轴长加上辐射源的高程H。但目标辐射源的高程一般来说未知，这时可通过假定目标高程来获取R，并进一步利用时差方程求解目标位置。一般来说,假定的高程与目标的实际高程存在误差，这个误差会影响最终的定位精度，但飞机等重点关注的目标运动高度一般在20 km以下，即最大高程误差为20 km，且通过信号特征、内涵等其他情报信息得到的目标高程估计值后，能获得理想的定位精度。

通过测量得到时频差后，可首先采用球面地球模型，解算出辐射源的初始位置，即利用以下方程：

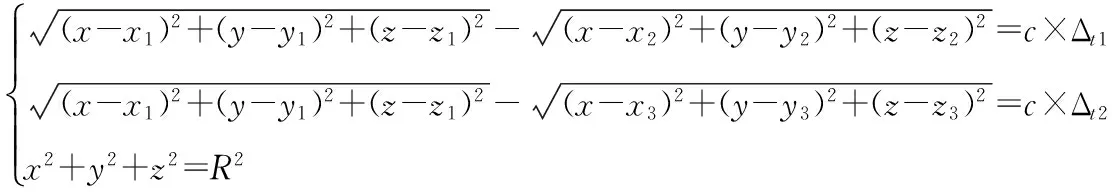
(3)

式中：x、y、z为未知数。该方程组为非线性方程组，其数值解过程如下[9-10]：令

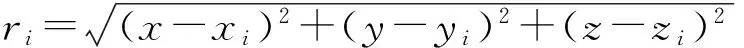
(4)

ri,1=ri-r1，

(5)

则变换可得辐射源位置u=[x,y,z]T，表示为

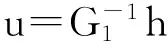
(6)

其中：

(7)

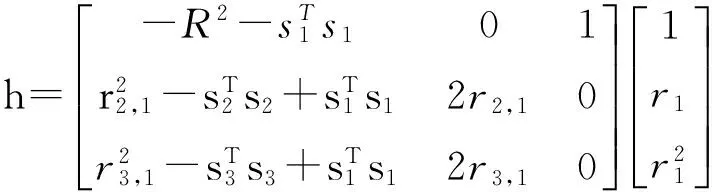
(8)

又uuT=R2，可得关于r1的一元四次方程，通过解该方程可得r1，然后利用式(1)可获取目标辐射源位置。一般求解r1会得到两个有意义的解，需要解模糊。

在获取目标的初始位置后，可采用牛顿迭代法在WGS-84(World Geodetic System 1984)模型下进行迭代计算获取目标辐射源的精确位置[6]。令

(9)

(10)

迭代方程为

u(k+1)=u(k)-[H(u(k))]-1×F(u(k)) 。

(11)

通过迭代就可获取辐射源的精确位置。

2.2测速处理算法

测速处理首先进行WGS-84模型下速度矢量的坐标转换。根据WGS-84模型中纬度B、经度L、高程H与XYZ坐标的关系[11]

(12)

可得速度转换关系为

(13)

式中：N、M分别为卯酉圈曲率半径和子午圈曲率半径，且

(14)

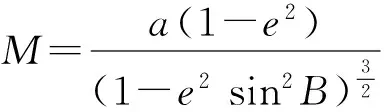
(15)

式中:a为地球长半轴长，取6 378 137 m;e为偏心率，e2取0.006 694 379 990 13。将转换关系代入频差方程可得

(16)

其中:

他并没有怨恨我。他说一看到床下的夜壶被人动过，就知道坏事了。他又说钱肯定是没了，只要人好好的，钱算啥？钱不算什么。将近十万块钱，咱要吸取这个教训。只要你坚持读大学，我砸锅卖铁还支持你。

(17)

(18)

式中：u为利用时差方程求解到辐射源位置；c为光速；fc为信号载频;Δf1、Δf2为主星接收信号与辅星A接收信号、辅星B接收信号的频差。

3性能仿真

3.1仿真场景

定位分析场景如图3所示，主星、辅星A、辅星B均为地球同步轨道卫星，3颗卫星在地面投影的特性为主星不动，辅星A、辅星B绕主星运动，并近似维持等腰直角三角形构型，星间距约为3 000 km。利用STK软件进行了星座设计，模拟卫星真实在轨环境并获取星历数据用于仿真分析。

图3　定位分析场景

一般来说，定位精度、测速精度与平台的位置、速度、星间距、时差测量、频差测量精度、辐射源相对于星座的位置、高程估计误差等因素有关。本文采用以前工程实现中的参数设置，平台位置误差为50 m，速度误差为0.1 m/s，且信号处理系统时间同步精度35 ns，频率稳定度10-10，如无特殊说明本文性能仿真中均采用此系统误差值。

3.2与传统差分测速的比较分析

传统的测速方法之一为利用两次定位的结果进行差分的方式进行测速。图4给出了本文方法与传统方法不同频差误差δf对测速误差δv的影响。

图4　与传统算法性能比较

传统差分法需要累积一定的观测时间才能获得可用的测速精度。仿真分析表明，差分法累积30 s和50 s的性能分别相当于本文算法频差测量精度14 Hz和10 Hz时的性能。在时频差测量算法中，累积0.1 s就能达到0.2 Hz量级的频差精度，所以本文算法比传统差分法具有优势。

3.3时频差误差对定位与测速精度的影响

三星时频差定位与测速技术中，主要测量参数时差和频差对定位与测速的精度影响较大。距离主星星下点[3 000 3 000] km处，不同高程误差条件下，在频差测量精度0.2 Hz，时差测量误差δt对定位精度δp与测速精度δv的影响，以及时差测量精度100 ns，频差测量误差δf对定位精度δp与测速精度δv的影响分别如图5和图6所示。仿真分析结果表明，时差测量误差越小，定位和测速精度越高。时差测量误差小于500 ns时，定位精度优于11 km。时差精度提高带来的测速精度提高主要原因是时差精度提高后测速方程中目标位置精度提高。频差测量误差主要影响测速精度，其误差越大，测速精度越差，在频差误差小于0.4 Hz时，在测速精度优于2 m/s。频差测量精度对定位精度无影响是因为定位方程中没有采用频差量。

(a)对定位精度影响

(b)对测速精度的影响

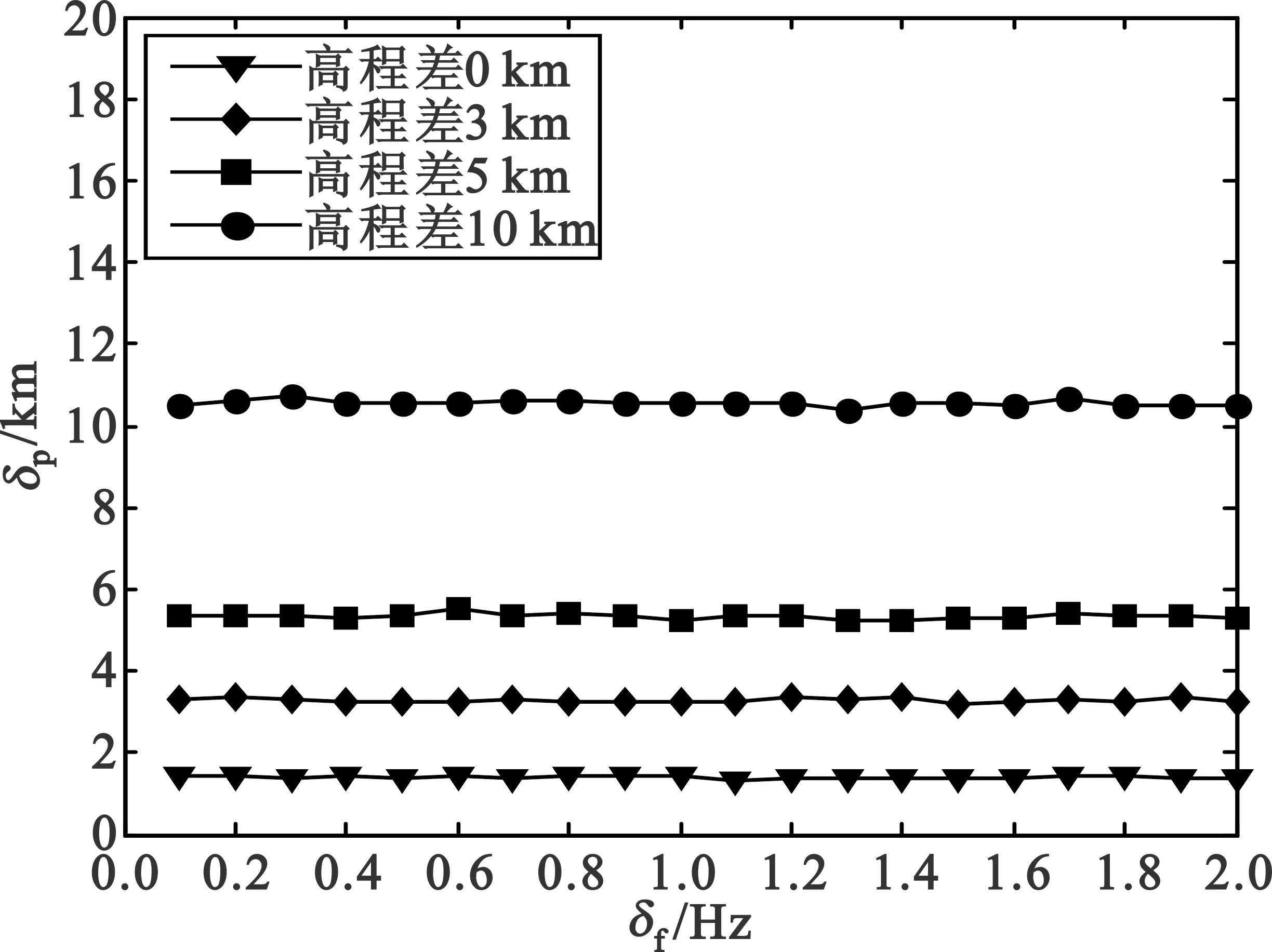
(a) 对定位精度影响

(b) 对测速精度的影响

3.4高程估计误差对定位与测速精度的影响

高程误差10 km条件下，定位点分布如图7所示，目标真实位置归一化到[0 0]km。

图7　距主星星下点3 000 km处定位分布图

从图中可看出由于高程存在估计误差，定位分布偏离真实位置。高程误差越大，定位精度越差，由于定位精度恶化，测速精度也变差。图8给出了不同位置高程误差δh对定位δp与测速精度δv的影响。

(a) 对定位精度影响

(b) 对测速精度的影响

仿真分析结果表明，高程估计误差越大，定位与测速精度越差。其主要原因数值方法迭代求解方程组实际为一个使方程组中各方程左右两端误差值之和最小化的过程，所以R引入的误差项必然分散到方程组中未知参数x、y、z的解中，从而增大解得误差。在高程估计误差小于3 km时，大部分覆盖区域内定位精度优于10 km，测速精度优于15 m/s。

4结束语

本文基于高轨三星时频差测量信息，提出了一种基于高程值估计的对运动辐射源进行定位与测速的方法，并分析了时差测量误差、频差测量误差、高程估计误差对定位与测速精度的影响。仿真分析表明，时频差测量精度越高,定位与测速精度越高。该方法可应用于高轨三星系统，实现对空中恒定高度运动的目标辐射的卫星上行信号、雷达信号等进行瞬时观测定位与测速，其定位与测速精度优于传统方法，可以进行工程应用。但该方法存在一定的不足，即高程估计误差较大时，对距离星下点较远位置处定位精度恶化较大，需要进一步分析，并研究解决方法。

参考文献：

[1]陆安南,孔宪正.单星测频无源定位法[J].通信学报,2004,25(9)：160-168.

LUAnnan,KONG Xianzheng.Passive localization from frequency measurements by single satellite[J].Journal of China Institute of Communications,2004,25(9):160-168.(in Chinese)

[2]AMAR A,WEISS A J.Localization of narrowband radio emitters based on Doppler frequency shifts[J].IEEE Transactions on Signal Processing,2008,56(11):5500-5508.

[3]徐义,郭福成,冯道旺.一种单星仅测TOA无源定位方法[J].宇航学报,2010,31(2)：502-508.XU Yi,GUO Fucheng,FENG Daowang.A new satellite passive localization method using TOA measurement only[J].Journal of Astronautics,2010,31(2):502-508.(in Chinese)

[4]HAWORTH D P,MITH N G S,BARDELLI R,et al.Interference localization for EUTELSAT satellites -the first european transmitter location system[J].International Journal of Satellite Communications,1997,15:155-183.

[5]彭华峰,夏畅雄,曹金坤.基于最小二乘融合估计的双星时频差定位[J].电讯技术,2012,52(4):435-438.

PENGHuafeng,XIA Changxiong,CAO Jinkun.Geo-location using dual-satellite’s TDOA and FDOA data by least square fusion estimation[J].Telecommunication Engineering,2012,52(4):435- 438.(in Chinese)

[6]钟丹星,邓新蒲,周一宇.基于WGS-84地球椭球的三星时差定位算法[J].航天电子对抗,2003(3):18-21.

ZHONG Danxing,DENG Xinpu,ZHOU Yiyu.A three satllite TDOA geolocation algorithm based on WGS-84 earth model[J].Aerospace Electronic Warfare,2003(3):18-21.(in Chinese)

[7]STEIN S.Algorithms for ambiguity function processing[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1981,29(3):588-599.

[8]GOH S S,GOODMAN T N T,SHANG F C.Joint estimation of time delay and Doppler shift for band-limited signals[J].IEEE Transactions on Signal Processing,2010,58(9):4583-4594.

[9]HO K C,CHAN Y T.Geolocation of a known altitude object from TDOA and FDOA measurments[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(3):770-783.

[10]HO K C,XU W W.An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J].IEEE Transactions on Signal Processing,2004,52(9):2453-2463.

[11]金郁萍.常用大地坐标系相互转换的设计与实现[D].成都：电子科技大学，2011.JIN Yuping.Design and implemention of earth coordinate transformation[D].Chengdu:University of Electronic Science and Technology of China,2011.(in Chinese)

A Mobile Emitter Localization and Velocity Estimation Method Using TDOA and FDOA Measurements from Three Satellites

ZHANG Yuyang

(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

Abstract：For the purpose of estimating location and velocity of moving target in three satellites system,a solution is presented for emitter passive location and velocity estimation using time-difference-of-arrival(TDOA) and frequency-difference-of-arrival(FDOA).Principles and process steps of the solution are described.The influence of TDOA measurement error,FDOA measurement error and altitude estimate error on location accuracy and velocity estimation accuracy is analyzed by Satellite Tool Kit(STK) and computer simulation.The proposed solution is accurate and efficient in locating and velocity estimating,which can be easily applied in engineering.

Key words：three satellites passive localization;mobile emitter;velocity estimation;TDOA;FDOA

doi:10.3969/j.issn.1001-893x.2016.06.008

收稿日期：2015-11-18；修回日期：2016-03-07Received date:2015-11-18；Revised date：2016-03-07

通信作者：ezhangyy@163.comCorresponding author：ezhangyy@163.com

中图分类号：TN97

文献标志码：A

文章编号：1001-893X(2016)06-0640-06

作者简介：

张宇阳(1985—)，男，四川成都人，2010年于电子科技大学获硕士学位，现为工程师，主要研究方向为数字信号处理、无线通信、辐射源定位。

ZHANG Yuyang was born in Chengdu,Sichuan Province,in 1985.He received the M.S. degree from University of Electronic Science and Technology of China in 2010.He is now an engineer.His research concerns digital signal processing,wireless communications,source localization.

Email:ezhangyy@163.com

引用格式：张宇阳.利用三星时频差的运动辐射源定位与测速方法[J].电讯技术，2016,56(6):640-645.[ZHANG Yuyang.A mobile emitter localization and velocity estimation method using TDOA and FDOA measurements from three satellites[J].Telecommunication Engineering,2016,56(6):640-645.]