一种利用询问-应答规律对应答机定位的方法*

曾　斌

(中国西南电子技术研究所，成都 610036)



一种利用询问-应答规律对应答机定位的方法*

曾斌**

(中国西南电子技术研究所，成都 610036)

摘要：针对双站测向定位系统复杂、同步要求高的问题，根据询问应答机的工作规律，提出了一种对应答机单站定位的方法。根据已知的地面询问站和侦收站位置，通过测量敌我识别询问和应答信号到达时间差和应答信号方位，实现了对应答机的定位；同时分析了定位误差，通过计算机仿真证明了该方法的可行性。在地面询问站已知的情况下该方法对于解决实际工程问题具有借鉴意义。

关键词：无源定位；敌我识别；询问-应答信号；到达时间差

1引言

敌我识别系统通过协同的方式工作，询问机发射询问编码信号，应答机检测到询问信号，进行译码处理判决后，通过应答天线发回应答编码信号来完成目标的识别。对于侦收系统，飞机、舰船等运动目标威胁较大，其搭载的应答信号是感兴趣的对象，需要对应答信号进行定位和跟踪，从而掌握目标的属性、状态和威胁程度等。

无源定位隐蔽性好，抗干扰能力强[1]。传统的测向定位和时差定位方法需要利用多站对同一辐射源测向或测时差[2-3]，系统比较复杂。采用单站对目标定位需要观测站运动，对动目标定位时甚至要求观测站机动[4-5]。在对应答机定位时，这些方法虽然可用，但如果利用询问-应答规律，可以简化系统设计。本文利用敌我识别询问和应答机工作规律，在地面询问站和观测站位置已知情况下，通过测量询问和应答信号到达时间差以及应答信号方位，实现对应答机定位。该方法可以降低系统复杂度，实现对目标的实时定位和跟踪。

2定位原理

2.1定位模型

为便于表述，本文以二维为例来讨论问题。如果增加俯仰角的测量，结论也容易推广到三维情况。对敌我识别应答信号的单站定位原理如图1所示。

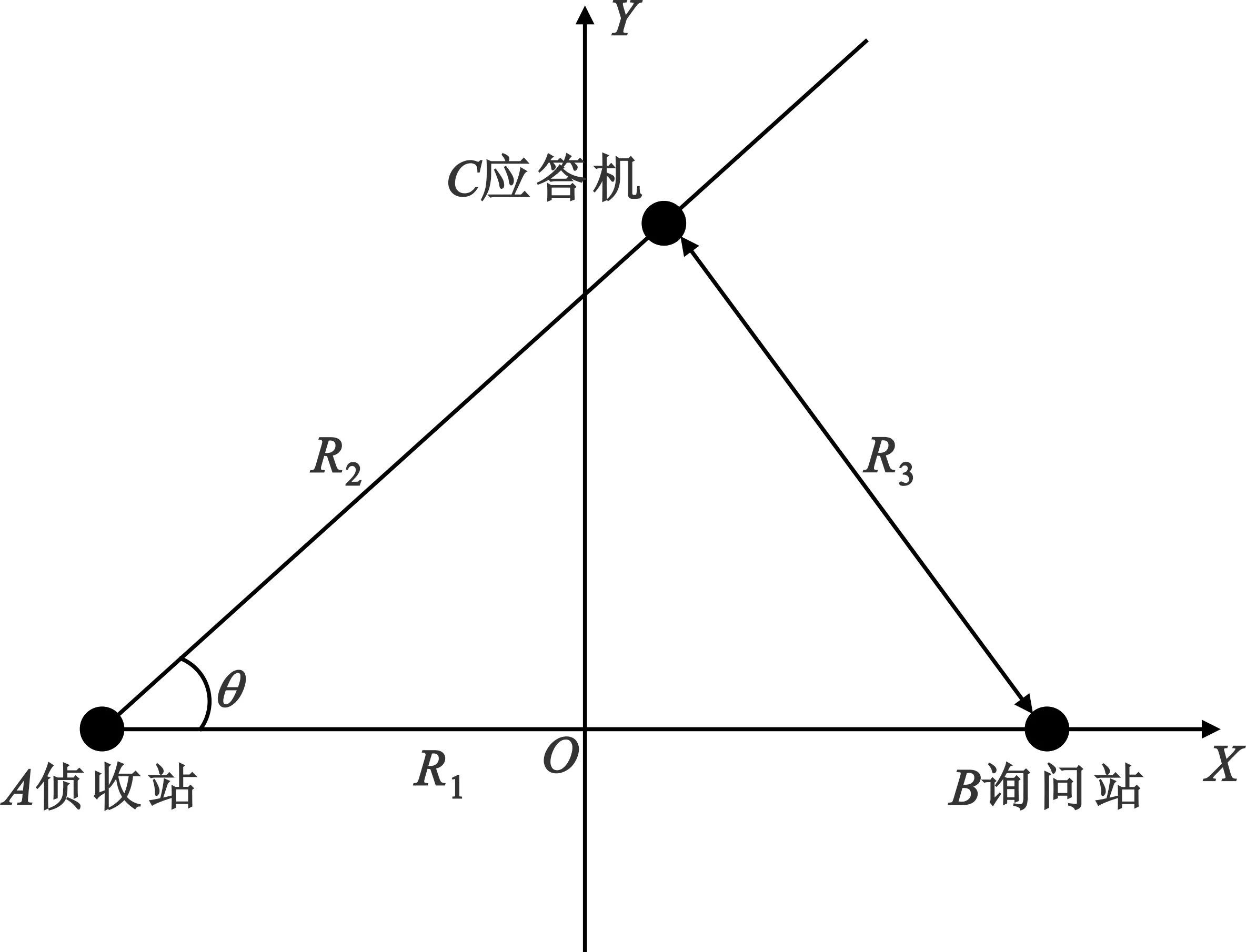
图1　敌我识别单站定位原理图

如图1所示，侦收站位置已知，针对地面固定询问站，其位置通过情报等其他手段可以获取。以侦收站和询问站的中点为坐标原点，两站之间连线为X轴建立坐标系，则侦收站坐标为A(x1,y1)，询问站坐标为B(-x1,y1)，应答机坐标为C(xT,yT)，侦收站通过干涉仪测得应答信号的方位角为θ。

询问站采用固定重复周期(PRI)方式询问，询问周期是ms量级。当侦收站、询问站和应答机之间的距离差在300 km以内时，可不考虑时差模糊。在短时间(1 s)内，动目标位置变化相对于到侦收站距离是一个极小量,因此信号出现规律可由图2表示。

图2　询问/应答信号出现时间规律

由图2可见，以询问站发出询问信号为时间0点，我们不能测量出应答信号发出的时间、询问站接收到应答信号的时间，但是能得到接收的询问信号和应答信号出现的时间，即t2、t3可以得到。根据电磁波传播规律，可以得出

c·(t2-t0)=R1，

(1)

c·(t1-tr-t0)=R3，

(2)

c·(t3-t1)=R2。

(3)

式中：tr为应答机的应答延时，为3 μs。由上面可以得到

c·(t3-t2)=R2+R3-R1+c·tr,

(4)

整理可得

R2+R3=c·(t3-t2)+R1-c·tr。

由此可见，目标位置就是到接收站和询问站距离和一定的点，这个点形成的轨迹是椭圆，椭圆方程为

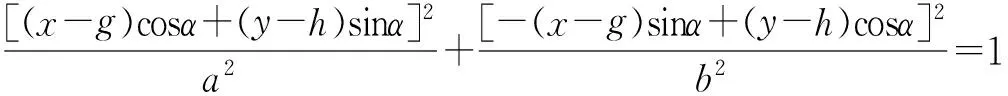
(5)

侦收站和应答机形成的直线方程为

y-y1=tg(θ)(x-x1) 。

(6)

由方程组(5)和(6)可以解得目标坐标的定位结果为

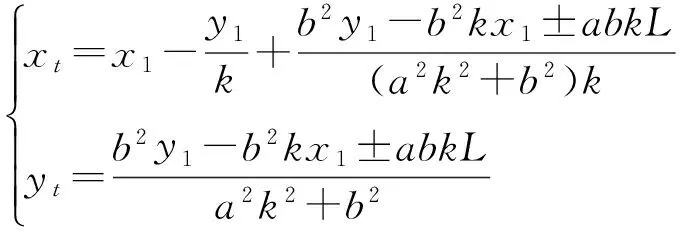
(7)

2.2定位误差分析

定位误差主要与测向误差、时差误差、接收站和询问站自身位置误差、应答时延波动有关。对定位结果进行全微分，可得出

(8)

(9)

(10)

其50%圆概率误差半径r0.5近似为

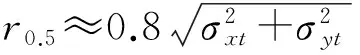
(11)

则相对定位误差为

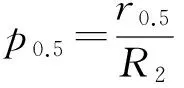
(12)

式中：取R2为辐射源与侦收站的距离。

2.3多次定位方法

单次定位精度不高，不能满足实际需要，因此需要多次定位。在多次测量的情况下，为了提高定位精度，通常选择适当的线性跟踪滤波算法如非线性最小二乘或卡尔曼滤波(KF)方法及其改进法等对辐射源进行跟踪定位[6]。

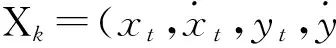
状态方程：

Xk=ΦXk-1+ΓWk-1。

(13)

测量方程：

1.精心备课。教师在备课的时候，要对教学内容深思熟虑，找出因果联系正好在哪里挂钩、初看起来不易察觉的那些交接点，因为这些地方会出现疑问，而疑问最能够激发求知欲望。教师必须知道：哪些东西要讲，而哪些东西则应留着给学生的思维埋下一小段“引火线”。

Yk=CXk+Vk。

(14)

其中:

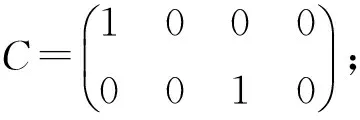
Wk是高斯扰动噪声，协方差矩阵为Qk；Vk为高斯测量噪声，协方差矩阵为Ri。这是标准的线性卡尔曼滤波方程，采用常规卡尔曼滤波处理步骤可以完成。通过滤波处理，可以实现对定位结果的优化，提高定位精度，并实现对动目标跟踪。

3仿真分析

3.1定位误差曲线分析

由定位误差均方差公式可以得到定位误差主要与测向误差、测时间差误差关系较大。下面通过仿真来说明。

仿真条件：为了计算方便，以侦收站和询问站中点为坐标原点，设侦收站位置坐标为(-100，0)km，应答机时延波动量为0.5 μs，平台自身位置误差分别为50 m、500 m，测向误差分别为2°、5°，时差测量误差分别为1 μs、5 μs。

3.1.1不同测向误差对定位的影响

条件：应答机时延波动0.5 μs，平台身位置误差50 m，时差测量误差1 μs，设测向误差分别为2°、5°时的定位误差。

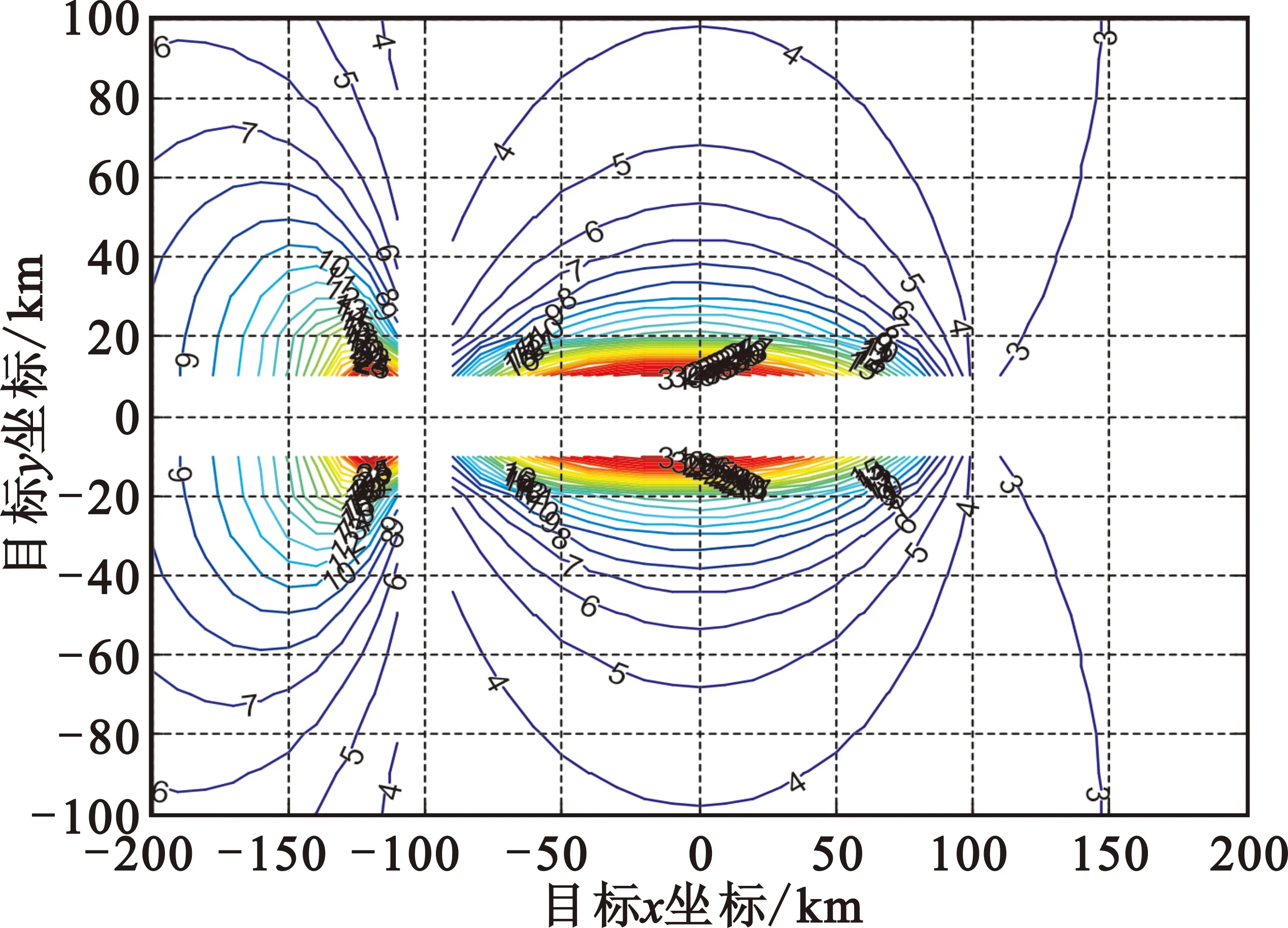
图3　测向精度2°时定位误差

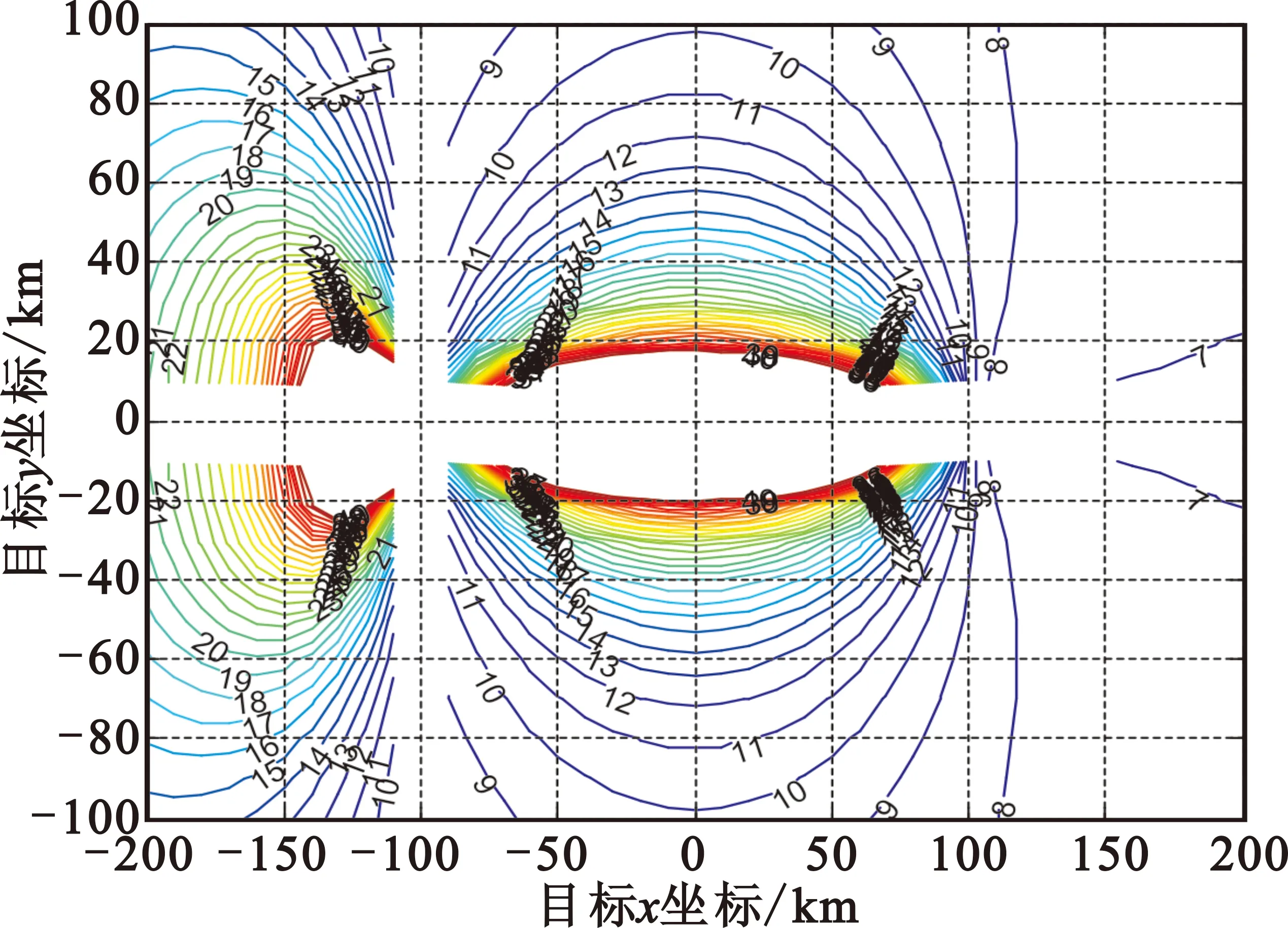
图4　测向精度5°时定位误差

3.1.2不同测时差精度对定位的影响

条件：应答机时延波动0.5 μs，平台身位置误差50 m，测向误差为2°，设时差测量误差分别为0.1 μs、5 μs时的定位误差。

仿真结果如图5和图6所示。由图可知，随着时差误差增大，定位误差增加,但时差测量误差对定位结果影响相对较小。

图5　时差精度0.1 μs时定位误差

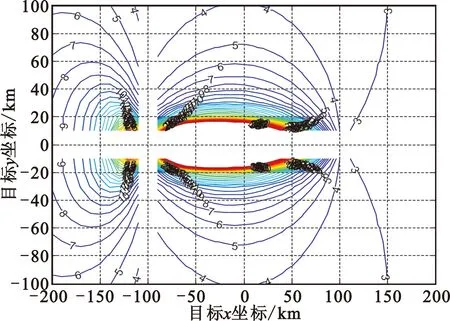
图6　时差精度5 μs时定位误差

3.1.3不同自身位置误差对定位的影响

条件：应答机时延波动0.5 μs，测向误差为2°，时差测量误差1 μs，设自身位置误差为500 m时的定位误差。

仿真结果如图7所示。由图可知，随着平台自身位置误差增大，定位误差有一定增加，但平台自身位置误差对定位结果影响很小。

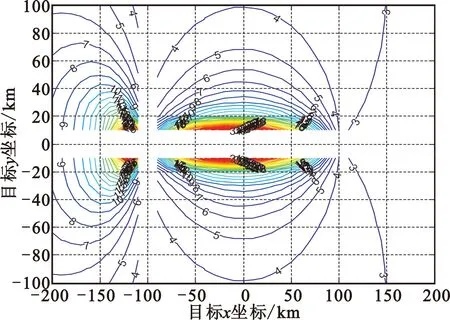
图7　平台自身位置误差500 m时定位误差

3.2多次定位的误差曲线

设目标做匀速直线运动，初始位置(50 km,50 km)，速度(50 m/s,0)，测向精度2°，时差测量精度1 μs，时间长度为100 s，蒙特卡洛实验次数为100。

仿真结果如图8和图9所示。由图可见，通过对多次定位结果的滤波处理，可以提高定位精度，并可能实现对目标的跟踪。现有的静止单站对动目标定位需要测多普勒，对测频精度的要求要达Hz量级，目前实现困难很大,而本文的方法却具有一定的可实现性。

图8　目标x方向速度估计值

图9　绝对定位误差

5结束语

在地面固定询问站位置已知的情况下，通过单站测量敌我识别询问和应答信号达到时间差，结合对应答信号测向可以实现对应答机定位。定位误差主要受测向和时差测量的影响，其中测向误差的影响较大。为提高定位精度并实现对动目标的跟踪，可通过多次定位结果的滤波进行处理。该方法在满足上述条件的情况下，在实际工程中具有一定借鉴意义。下一步需要进一步分析该方法的定位条件、时差模糊、机动目标跟踪等问题。

参考文献：

[1]刘聪锋.无源定位与跟踪[M].西安：西安电子科技大学出版社，2011.

LIU Congfeng.Passive location and tracking[M].Xi′an：Xidian Univereity Press,2011.(in Chinese)

[2]富森,孔祥维，李哲，等.多基纯方位目标交叉定位中的非线性最小二乘方法[J].火力与指挥控制,2009,34(8):80-83.

FU Sen，KONG Xiangwei,LI Zhe,et al.Bearing-only target cross location of multi-station based on nonlinear least squares[J].Fire Control & Command Control,2009,34(8):80-83.(in Chinese)

[3]杨甲胜,王喆,王志刚，等.无源到达时差定位技术分析[J].舰船电子对抗,2010,33(5):5-9.

YANG Jiasheng,WANG Zhe,WANG Zhigang,et al.Analysis of passive arrival time difference location technology[J].Shipboard Electronic Countermeasure,2010,33(5):5-9.(in Chinese)

[4]祝咏晨．单站无源定位技术的探讨[J]．信息技术,2005,29(6):63-64.

ZHU Yongchen.Research on single observer passive location[J].Information Technology,2005,29(6):63-64.(in Chinese)

[5]丁卫安.测向和测频改进的最小二乘单站定位跟踪方法[J].探测与控制学报,2011(1):61-64.

DING Weian.Single-station location and tracking methods on direction and frequency measurement combined with improved least-squares algorithm[J].Journal of Detection & Control,2011(1):61-64.(in Chinese)

[6]陈玲，李少洪．基于无源时差定位系统的机动目标跟踪算法[J].系统工程与电子技术，2005，27(1):127-130.

CHEN Ling,LI Shaohong.Algorithm of maneuvering target tracking with TDoA passive location system[J].Systems Engineering and Electronics,2005,27(1):127-130.(in Chinese)

A Locating Method Based on Regulation of Interrogate-response Signal

ZENG Bin

(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

Abstract：Based on the principle of interrogator,a new method for locating the responder with single station is proposed,which avoids the problem that the double-station locating system is complex and the requirement of synchronization is high.According to the known positions of the interrogator and the reconnaissance station on ground,by measuring the time-difference-of-arrival(TDOA) of the identification friend or foe(IFF) inquiry and response signal and the azimuth of response signal,the method can locate the responder,and the location accuracy is analyzed.The method has been proved practicable by computer simulation.The method has reference significance for solving practical engineering problems when the position of the inquiry station is known.

Key words：passive location;identification of friend or foe;interrogate-response signal;time-difference-of-arrival(TDOA)

doi:10.3969/j.issn.1001-893x.2016.06.007

收稿日期：2015-12-30；修回日期：2016-05-31Received date:2015-12-30；Revised date：2016-05-31

通信作者：zengbin0715@163.comCorresponding author：zengbin0715@163.com

中图分类号：TN971

文献标志码：A

文章编号：1001-893X(2016)06-0635-05

作者简介：

曾斌(1974—)，男，重庆人，博士，工程师，主要研究方向为信号处理及信息获取。

ZENG Bin was born in Chongqing,in 1974.He is now an engineer with the Ph.D. degree.His research concerns signal processing and information acquisition.

Email:zengbin0715@163.com

引用格式：曾斌.一种利用询问-应答规律对应答机定位的方法[J].电讯技术，2016,56(6):635-639.[ZENG Bin.A locating method based on regulation of interrogate-response signal[J].Telecommunication Engineering,2016,56(6):635-639.]