电波传播抛物方程模型在航空通信中的应用*

刘晓娣,周新力,侯松高

(1.海军航空工程学院 电子信息工程系，山东 烟台 264001；2.烟台特种设备检验研究院，山东 烟台 264001)



电波传播抛物方程模型在航空通信中的应用*

刘晓娣**1,周新力1,侯松高2

(1.海军航空工程学院 电子信息工程系，山东 烟台 264001；2.烟台特种设备检验研究院，山东 烟台 264001)

摘要：针对航空通信中电波传播损耗预测需要满足精确性、实时性及复杂环境适应性的要求，在分析电波传播损耗对航空通信系统作用范围的影响基础上，采用抛物方程模型研究了航空通信中电波在空间区域的传播特性。该模型利用分步傅里叶算法实现快速求解，采用边界平移法处理复杂地形边界，并通过非均匀网格技术提高空间任意一点的场强计算精度，从而改善了复杂环境下电波传播损耗预测的精确性和实时性。将该模型应用于真实地形环境下的航空通信仿真算例中，仿真结果表明：该模型能有效预测复杂环境下电波的传播损耗，评估在正常通信条件下飞行器的飞行范围、最大飞行距离以及最低飞行高度等性能。

关键词：航空通信；电波传播；抛物方程；复杂环境

1引言

在航空训练中，为保证飞行安全，需要飞行器与地面设备之间能够实时无线通信。飞行器与地面设备之间的电波传播损耗预测在航空通信中具有重要意义[1]：一方面，用于飞行器无线通信系统设计之前，设计开发人员可据此进行必要的调校；另一方面，用于通信试飞前进行通信距离地面摸底试验，可减少试飞架次，有效控制试飞成本；再次，用于飞行训练前，可估计飞行器的有效飞行范围。

飞行器根据执行任务的不同，飞行路径往往会选择在平原、丘陵、山区等复杂地形环境上空。合理预测通信电波在复杂环境中的传播损耗，是对航空通信精确性的挑战。同时，由于飞行器的飞行速度快，对传播损耗预测的实时性要求也很高。因此，航空通信中的电波传播损耗预测应满足精确性、实时性和复杂环境适应性的要求。

电波传播预测模型主要分为基于电波传播理论的确定性模型和基于数理统计方法的经验模型或半经验模型。由于确定性模型往往需要确定电波传播的边界条件，且计算相当复杂，实时性不高，在航空通信电波传播损耗预测的现有研究中，多采用经验模型或半经验模型[1-2]。但经验模型或半经验模型是基于大量实验数据统计分析建立的，具有地区局限性，预测精度不高，且只能得到某一方向上指定高度的传播损耗。抛物方程(Parabolic Equation,PE)作为一种确定性模型，最早由Leontovich和Fock在20世纪40年代提出，是一种前向全波法，能够同时处理非均匀媒介和复杂边界条件，采用快速傅里叶算法可实现快速求解，已被应用于复杂环境下的信道建模中[3-5]，而在航空通信方面的研究尚未见诸文献。因此，本文在分析电波传播损耗对航空通信系统作用范围的影响基础上，采用复杂地形条件下的PE模型预测电波在空间区域的传播特性，并通过非均匀网格技术提高空间任意一点的场强计算精度，最后通过抽取航天飞机雷达地形测绘使命(Shuttle Radar Topography Mission，SRTM)高程数据获取详细地形边界，将该模型应用于真实地形环境下的航空通信仿真算例中，验证了该模型的有效性。

2问题提出

假设在航空通信系统中，地面发射机的高度为ht，飞行器的飞行海拔高度为hf，地形起伏高度为hg，飞行器沿AB方向飞行，如图1所示。在飞行过程中，由于复杂地形环境影响，在不同的位置，飞行器所接收到的地面发射机的信号强度存在较大差异，如飞行器飞经A点时，处于发射机的视距范围内，接收信号以直射波、反射波为主；当飞经B点时，受山体阻挡，接收信号以绕射波为主；此外，电波在空间传播，还存在大气折射现象。不管电波以何种形式传播，飞行器在空中飞行时，接收到地面发射机的信号强度大于等于飞行器接收机的接收灵敏度，则认为飞行器能够与地面设备保持正常通信。

图1　航空通信示意图

假设地面设备的发射功率为PT，天线增益为GT，飞行器接收机的天线增益为GR，系统综合损耗LS，电波在飞行路径上的传播损耗为Lb，则接收机的接收功率为

PR=10lgPT+GT+GR-LS-Lb。

(1)

假设飞行器接收机的接收灵敏度为SR，由式(1)可建立传播损耗与航空通信的关系。设门限为T，则

T=10lgPT+GT+GR-LS-SR。

(2)

当Lb≤T时，飞行通信正常。其中等号表示临界通信，对应了满足航空通信要求下飞行器的最大飞行界限。由电波传播模型预测出飞行路径上任一点的传播损耗Lb，就可以确定满足飞行器的飞行范围、在指定高度下的最远飞行距离以及在指定距离处的最低飞行高度等性能参数。

3基于PE模型的电波传播特性预测

3.1复杂地形条件下的PE模型

假设电波在无源媒介中传播，电磁场的时谐因子为e-iωt。在直角坐标系Oxyz中，二维标量波动方程只考虑电波的前向传播，并采用Feit-Fleck近似得到宽角PE[6]为

ik(m-1)u(x,z)。

(3)式中：k=2π/λ为真空中的传播常数；λ为电波波长；m=n+z/ae为修正折射率,n是传播媒介的折射率,ae为地球的半径；x、z分别表示传播距离和传播高度。

利用分步傅里叶变换法求解可得

(4)

利用PE模型求解电波传播问题时，需考虑初始场分布、上方的吸收边界和下方的地表边界。对于初始场，可先由格林函数法求得自由空间的口径场，再根据双射线模型得到地表以上半空间的初始场分布。对于上边界，可利用Turkey窗函数来实现有限高度范围上的吸收边界。对于地表下边界，当电波沿复杂地形边界传播时，需要先对不规则地形边界进行处理，然后再使用平面阻抗边界条件下离散混合傅里叶变换来求解。在此采用边界平移法[7]处理地形下边界，基本原理如图2所示：首先通过计算步进迭代时地形的高度差zdiff，确定平移的垂直网格数；然后根据zdiff的符号确定平移的方向，若为正则向上平移，若为负则向下平移，若等于0则维持不变。由此，可以求得复杂地形边界以上各均匀网格点的场分布。

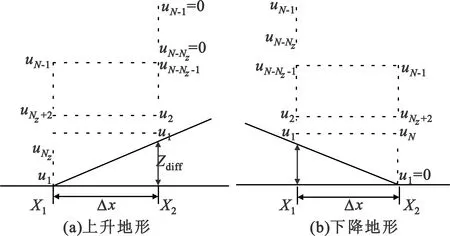
图2　边界平移法示意图

3.2空间任意一点场值的求解

当飞行器飞行至目标上空P(X,Z)点处，且P不位于任何网格点上时，在传统的PE计算过程中，一般通过线性插值的方法求解[8]非整格点处的场值,而在网格较大或环境较为复杂的情况下，这种处理方法往往会引入较大误差。在此，采用非均匀网格技术来求解P点处的场值，如图3所示。

图3　空间任意一点的场值求解

(1)水平方向

由于P点不在水平整格点上，到达P点的水平步长不再等于Δx，而是取水平距离X与Δx的余数，即

ΔxL=mod(X,Δx)。

(5)

这样就将P点转换到水平网格点上，然后再利用离散混合傅里叶变换来求解。

(2)垂直方向

P点在垂直方向上相对于PE的网格存在偏移ΔzL：

ΔzL=mod(Z,Δz) 。

(6)

由式(4)可知，SSFT通过场值在高度域和变换域之间的映射，实现了折射、绕射因子的分离。根据两域的映射关系，由傅里叶变换平移性质可知，在垂直方向上偏移ΔzL后的场值为[8]

u(x,z-ΔzL)=F-1{F[u(x,z)]exp(-ipΔzL)}。

(7)

因此，首先在水平方向进行变换步长的PE计算，得到在水平距离X处沿垂直方向各整格点上的场值；然后再由垂直方向的平移变换，得到P点的场值。

4仿真算例

以超短波通信系统为例，假设地面发射机的工作频率为300 MHz，全向天线，水平极化；发射机的坐标为(E116.8°，N44.1°)，天线高度为100 m。飞行器向着坐标为(E118.4°，N43.4°)的目标方向飞行。标准大气条件，中等干燥地面。PE的计算高度为2 500 m。为使仿真条件贴近实际航空通信环境，从SRTM 3高程数据中提取地形剖面，如图4所示。

图4　地形剖面图

利用本文第3节中的方法计算得到地面发射机沿飞行方向的电波传播损耗空间分布伪彩图，如图5所示。由于复杂地形的影响，在山峰背后电磁能量会发生衰减，尤其是经过最高峰之后电磁能量明显减小。其中，在近距离范围内，图5中未给出较大高度点上传播损耗的有效计算结果。这是因为在此范围内较大高度上对应的计算仰角会很大，超出了Feit-Fleck型宽角PE的计算仰角，不适合用宽角PE来计算，在后面的分析中对该范围未作考虑。

图5　传播损耗空间分布伪彩图

假设飞行器在一段时间内飞行的海拔高度变化不大。从图5中抽取海拔高度1 850 m的传播损耗值，如图6所示，左坐标表示地形高程值，其中发射机位于地形的最左端；右坐标表示电波传播损耗值。

图6　1 850 m高度的传播损耗随距离的变化

从图中可以看出在最高峰之前，传播损耗随距离的增大而缓慢增长，且传播损耗曲线发生上下振荡。这是因为在该区域，飞行器与发射机之间无障碍物，且飞行器与地面的距离较大，地形对该高度处的电波传播影响很小；曲线的振荡现象是由地形上升区域直射波与反射波之间的干涉作用造成的。在最高峰后，传播损耗值发生陡增，由122 dB增至134 dB，此后电波传播以绕射衍射为主。在最高峰和次高峰之间，相距不足21 km，由于地形的阻挡，传播损耗值发生急剧变化，由134 dB增至150 dB。而在最高峰和次高峰处，传播损耗有所减小且存在振荡，这是电波遇到山峰阻挡被反射回来时与原有波相干涉的结果。随着距离的增大，地形高度降低，与飞行器的间距变大，地形对电波传播的影响也变得很小，传播损耗值呈缓慢增长趋势。该结论与文献[1]中采用Longley -Rice模型对地形的影响分析一致。

假设地面设备的发射功率为10 W，收发天线增益共为6 dB，系统综合损耗为6 dB，飞行器接收机的灵敏度为-110 dBm。根据航空通信模型，在正常通信的条件下计算对应的电波传播损耗门限T=150 dB，对图5的传播损耗空间分布作阈值化处理，得到飞行器在2 500 m以下、与地面发射机正常通信条件下的飞行范围如图7中间区域所示。结合图5和图7，可得到不同高度上飞行器的最远飞行距离以及不同距离处在2 500 m以下的最低飞行高度，如图8和图9所示。从图8中可以看出:在1 850 m高度上飞行器的最远飞行距离为89 km，而2 100 m高度上飞行器的最远飞行距离为116 km；在80 km距离处的最低飞行高度为1 766 m，而在130 km距离处2 500 m以下的最低飞行高度为2 226 m。

图7　正常通信条件下飞行器的飞行范围

图8　不同高度上飞行器的最远飞行距离

图9　不同距离处在2 500 m以下的最低飞行高度

5结束语

针对航空通信中电波传播损耗预测对精确性、实时性及环境复杂性的要求，本文采用复杂地形条件下的PE模型，研究了航空通信中电波的空间传播特性以及空间任意一点的场值计算方法，并仿真分析了该模型在真实地形环境下航空通信中的应用。理论分析与仿真算例表明该模型能有效改善复杂环境下电波传播损耗预测的精确性和实时性，评估正常通信条件下飞行器的飞行范围、最远飞行距离以及最低飞行高度等性能，为确定航空通信系统的作用范围、保证飞行安全提供有力支撑。由于PE计算仰角的局限性，无法给出近距离较大高度上传播损耗的有效计算结果，文中对此未作考虑。而实际应用中在近距离处飞行器处于起飞阶段，飞行高度有限且该区域的传播损耗较小，一般不会影响正常的航空通信。文中方法为航空通信系统的作用范围提供了有效的判定方法，但仅在二维垂直剖面内展开研究，对于三维空间中的应用问题后续将予以研究。

参考文献：

[1]张文波,曹耀钦.电磁环境仿真中电波传播模型研究及仿真分析[J].电波科学学报,2012,27(3):538-542.

ZHANG Wenbo,CAO Yaoqin.Research and simulation analysis on radio propagation model in electromagnetic environment simulation[J].Chinese Journal of Radio Science,2012,27(3):538-542.(in Chinese)

[2]刘满堂,张家新,刘悦.复杂电磁环境下航空通信效能试飞评估[J].电讯技术,2015，55(2):222-225.LIU Mantang,ZHANG Jiaxin,LIU Yue.Evaluation of aeronautical communication effectiveness through flight-test in complex electromagnetic environment[J].Telecommunication Engineering,2015,55(2):222-225.(in Chinese)

[3]GADWAL V,BARRIOS A E.Channel modeling using the parabolic equation for RF communications[C]// Proceedings of 2009 IEEE Military Communications Conference(MILCOM 2009).Boston:IEEE,2009:18-21.

[4]GADWAL V,BELANGER D J,BARRIOS A E,et al.Wideband channel modeling in real atmospheric environments with experimental evaluation[R].San Diego:Space and Naval Warfare Systems Center Pacific,2013.

[5]肖金光,刘晓娣,周新力,等.基于PE的海洋蒸发波导宽带通信信道建模方法[J].计算机仿真,2015,32(11):216-220.

XIAO Jinguang,LIU Xiaodi,ZHOU Xinli,et al.A method of wideband channel in sea evaporation duct communication based on PE[J ].Computer Simulation,2015,32(11):216-220.(in Chinese)

[6]FEIT M D,FLECK J A.Light propagation in graded-index gibers[J].Applied Optics,1978,17(24):3990-3998.

[7]SPRAGUE R A,PATTERSON W L,BARRIOS A E.Advanced propagation model(APM) version 2.1.04 computer software configuration item(CSCI) documents[R].San Diego:Space and Naval Warfare Systems Command,2007.

[8]胡绘斌.预测复杂环境下电波传播特性的算法研究[D].长沙:国防科技大学,2006.HU Huibin.Algorithms on predicting characteristics of radio propagation in complex environments[D].Changsha:National University of Defence Technology,2006.(in Chinese)

Application of Wave Propagation Model Based on Parabolic Equation in Aeronautical Communication

LIU Xiaodi1，ZHOU Xinli1，HOU Songgao2

(1.Department of Electronic Information Engineering,Naval Aeronautics and Astronautics University,Yantai 264001,China;2.Yantai Special Equipment Inspection Institute,Yantai 264001,China)

Abstract：The parabolic equation(PE) model is used to predict the wave propagation characteristics for the demands of accuracy,timeliness and environmental complexity in aeronautical communication.The influence of propagation loss on the aeronautical communication range is analyzed.The split-step Fourier transform(SSFT) technology is used to solve the PE,boundary shift method is used to deal with the complex terrain,and un-uniform grid technology is used to advance the precision of the field at any point in space.The model is applied to aeronautical communication simulations in the real terrain environment.Numerical simulations demonstrate this model can predict wave propagation loss in complex environment correctly,and evaluate the flight range,the farthest flight distance and the lowest flight height effectively in normal communication.

Key words：aeronautical communication;wave propagation;parabolic equation;complex environment

doi:10.3969/j.issn.1001-893x.2016.06.005

收稿日期：2015-12-18；修回日期：2016-03-04Received date:2015-12-18；Revised date：2016-03-04

基金项目：国家自然科学基金资助项目(61179016)

Foundation Item:The National Natural Science Foundation of China(No.61179016)

通信作者：xdl_1982@163.comCorresponding author：xdl_1982@163.com

中图分类号：TN011

文献标志码：A

文章编号：1001-893X(2016)06-0624-05

作者简介：

刘晓娣(1982—)，女，山东昌邑人，2007年于国防科技大学获硕士学位，现为工程师、博士研究生，主要从事无线电波传播、信号处理研究；

LIU Xiaodi was born in Changyi,Shandong Province,in 1982.She received the M.S. degree from National University of Defense Technology in 2007.She is now an engineer and currently working toward the Ph.D. degree.Her research concerns wave propagation and signal processing.

Email:xdl_1982@163.com

周新力(1964—)，男，山东寿光人，教授、博士生导师，主要从事无线通信、无线电波传播研究；

ZHOU Xinli was born in Shouguang,Shandong Province,in 1964.He is now a professor and also the Ph.D. supervisor.His research concerns wireless communication and wave propagation.

侯松高(1981—)，男，山东莱州人，助理工程师，主要从事应用电子技术、特种设备检验检测研究。

HOU Songgao was born in Laizhou,Shandong Province,in 1981.He is now an assistant engineer.His research concerns applied electronics technology and special equipment inspection.

引用格式：刘晓娣,周新力,侯松高.电波传播抛物方程模型在航空通信中的应用[J].电讯技术，2016,56(6):624-628.[LIU Xiaodi，ZHOU Xinli，HOU Songgao.Application of wave propagation model based on parabolic equation in aeronautical communication[J].Telecommunication Engineering,2016,56(6):624-628.]