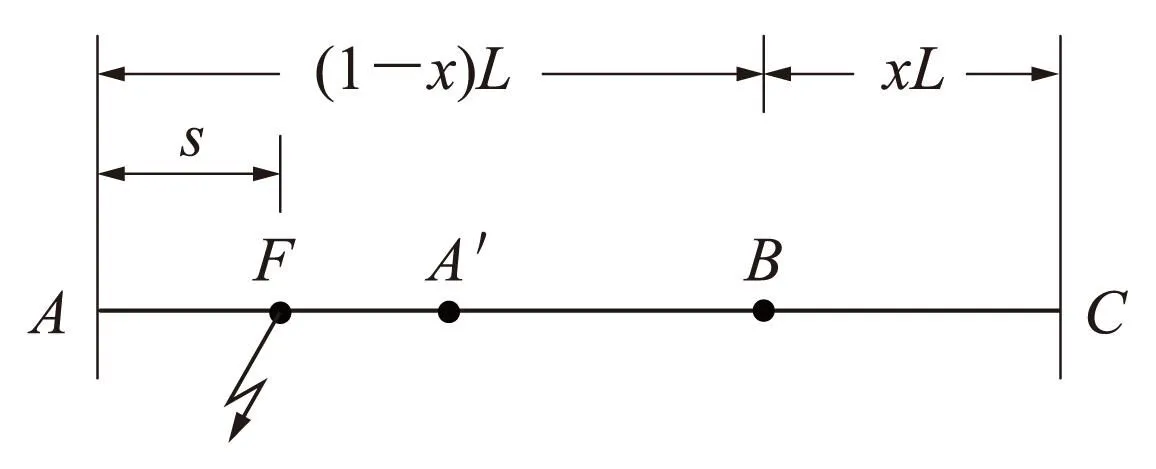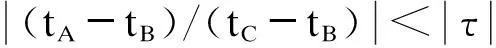消除波速影响的三端式行波故障测距方法

崔浩, 王丰华, 穆卡, 张君, 刘亚东

(1. 国网上海奉贤供电公司，上海201400；2. 电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海 200240)



消除波速影响的三端式行波故障测距方法

崔浩1, 王丰华2, 穆卡2, 张君2, 刘亚东2

(1. 国网上海奉贤供电公司，上海201400；2. 电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海 200240)

摘要：为了进一步提高输电线路行波测距方法的准确性，在分析波速不确定性导致的测距误差的基础上，提出一种消除波速影响的三端式行波故障测距算法。该方法通过在线路两端以及线路中间任一确定位置装设带有时间同步模块的行波测距装置，应用网格分形算法提取线路故障时初始行波的到达时间，基于行波传输距离与传播时间成正比，建立了关于故障初始行波到达各测量点时间的故障测距公式。理论分析与仿真结果均表明该方法不受行波传输速度的影响，能够有效提高输电线路故障定位的准确度。

关键词：故障测距；三端式；行波；网格分形算法

高压输电线路是电力系统的重要组成部分，线路发生故障会直接影响系统稳定性，因此，及时有效地对故障点进行定位，进而采取有效措施排除故障，对电网的安全稳定运行具有重要的意义。现有输电线路故障测距方法可分为两类：阻抗法与行波法。阻抗法利用已知的系统参数与故障后的稳态工频量列写故障测距方程，通过求解该方程得到故障点位置，但受故障过渡电阻、故障类型及线路结构不对称等因素的影响，测距精度有限。行波法根据线路故障时产生的电压、电流行波信息进行测距，其原理简单，测距精度高，可靠性与稳定性较好，已有较多的应用[1]。行波法的测距原理主要包括单端测距原理与双端测距原理[2]，前者通过测量到达线路端点的首个行波与其反射波间的时间差来计算故障距离[3]，后者利用线路两端行波到达的绝对时间差来计算故障点与线路两端的距离[4-5]。这两种测距原理均需采用预先设定的波速而非线路的实时波速来计算故障距离，二者若不相等，则会给测距结果带来误差；此外，单端测距受行波复杂的折反射影响而难以准确识别反射行波，可靠性较差[4]。为解决现有测距方法存在的问题，文献[5]提出分布式行波故障定位方法，对单端测距原理进行了改进，即根据多个检测点接收到的前4个行波波头时刻计算故障距离，该方法无需装设时间同步装置。为降低波速不确定性对现有单端和双端测距法的影响，文献[6]提出了一种输电线路区外故障情况下的行波速度在线测量方案。文献[7]利用故障初始行波与其在故障点及对端母线反射波的时间差建立测距方程，消除了波速的影响，但当行波的折反射较为复杂时，若无法准确识别初始行波的后续反射波，测距结果的误差仍较大。文献[8]利用相邻两条输电线路3个端点行波波头的到达时间构成三端式行波测距原理，消除了波速影响，但该方法是建立在相邻两条输电线路行波速度完全相同的前提下，对两条波速不同的输电线路来说，不仅不能有效消除波速对测距结果的影响，还会产生更大的误差。

为进一步提高输电线路的测距精度，本文提出一种消除波速影响的三端式行波测距算法，通过检测行波到达线路两端与线路中间任一确定位置的时刻，计算出故障发生位置。

1行波速度对现有测距方法的影响

三相线路各相之间存在耦合，难以直接求解线路波动方程，因此一般利用相模变换对三相线路进行解耦，将三相线路转化为相互独立的3个模量进行分析。凯伦布尔变换矩阵是实数矩阵，其运算量较小，常用于暂态高频行波分析[4-6]。本文采用凯伦布尔变换将三相电压、电流行波变换为独立的3个模量：模0分量、模1分量和模2分量。3个模量相互独立，其中模0分量为零模分量，模1与模2分量为线模分量。研究表明，线路零模电感随频率升高而明显降低，零模电容不受频率影响，则零模波速度随频率升高而明显增大，使得零模波速度不适用于单端及双端等传统测距方法[7]。而线路线模电感、电阻参数基本不受频率影响，因此，在同一条架空输电线上的线模行波传播速度可视为恒定值，本文后续分析均采用行波的线模分量。

各种行波测距原理均利用行波传播速度与传播用时构造测距公式，这两者即为影响行波测距精度的主要因素。现有文献一般取行波线模速度为0.936c～0.987c[7](其中c为光速)，显然，若波速预设值与线路实际波速不等，则对测距结果产生较大的影响。本文重点分析行波速度对单端测距法和双端测距法的影响。

1.1对单端测距法的影响

行波单端测距法利用测量端接收到的第一个故障行波与其在故障点反射波之间的时差计算故障距离。其测距公式为

式中：s1为故障点到线路首端行波测量点的距离，t1为故障行波波头到达行波测量点的时间，t2为故障点的第一个反射波波头到达行波测量点的时间，v为线路实际波速。

显然，单端测距法的绝对测距误差

(1)

式中：vs为用于计算故障距离的预设波速，Δv为实际波速与预设波速的差值。

由式(1)可知：当波速误差一定时，故障点距离行波测量端越远，造成的绝对测距误差越大。若取初始行波在对端母线的反射波进行计算，仍有相同的结论。

1.2对双端测距法的影响

行波双端测距法在线路两端装设具有时间同步模块的行波测距装置，通过测量故障初始行波到达线路两端的时间来计算故障距离。其测距公式为

式中：s2为故障点到线路首端的距离，thead为故障初始行波波头到达线路首端的时间，tend为故障初始行波波头到达线路末端的时间，L为输电线路长度。

双端测距法的绝对测距误差

(2)

由式(2)可知：当波速误差一定时，故障点越靠近线路两端，造成的绝对测距误差越大。

2基于网格分形的行波波头信号提取

利用行波的各类测距方法均需要准确获取故障行波到达测量点的时间，以建立测距公式，其关键在于初始行波信号奇异点的检测。小波变换在行波信号提取中已有较为广泛的应用[1-5]，然而如何选取合适的小波基函数是一大难点，若选取不当会造成较大的误差。近年来，分形算法已广泛应用于电能质量检测及故障分析等领域，有着良好的应用效果[9]。分形是对没有特征长度但具有一定意义的自相似图形和结构的总称，其研究对象为自然界和非线性系统中出现的复杂形体，分形度量为分形维数。对于离散化的数字信号，可将其视为数字化离散空间点集，当信号类型不同时，其分形维数一般不同，故分形维数能用于信号的识别与检测。本文参考网格分形维数定义，提出一种基于分形维数的行波信号奇异点检测方法，以期能准确、有效地检测故障行波波头的到达时刻。

定义：对于离散信号X，N(δ)表示在时间段[tk-Δt，tk]内以δ为边长的正方形网格覆盖信号X所需的网格数，其中tk为待处理信号的结束时刻，Δt为待处理信号的时长。在时间段[tk-Δt，tk]内，信号包含n+1(n为偶数)个采样点[x1，x2，…，xn+1]，令δ=Δt/n，则有

对于行波信号而言，故障发生前故障行波信号一直为零，此时N(δ)始终为0；故障发生后，在波头到达的时刻行波信号会发生突变，此时N(δ)随之变化。因此，利用网格数N(δ)可有效识别波头到达的时间，即N(δ)出现第一个极大值时所对应的时间。

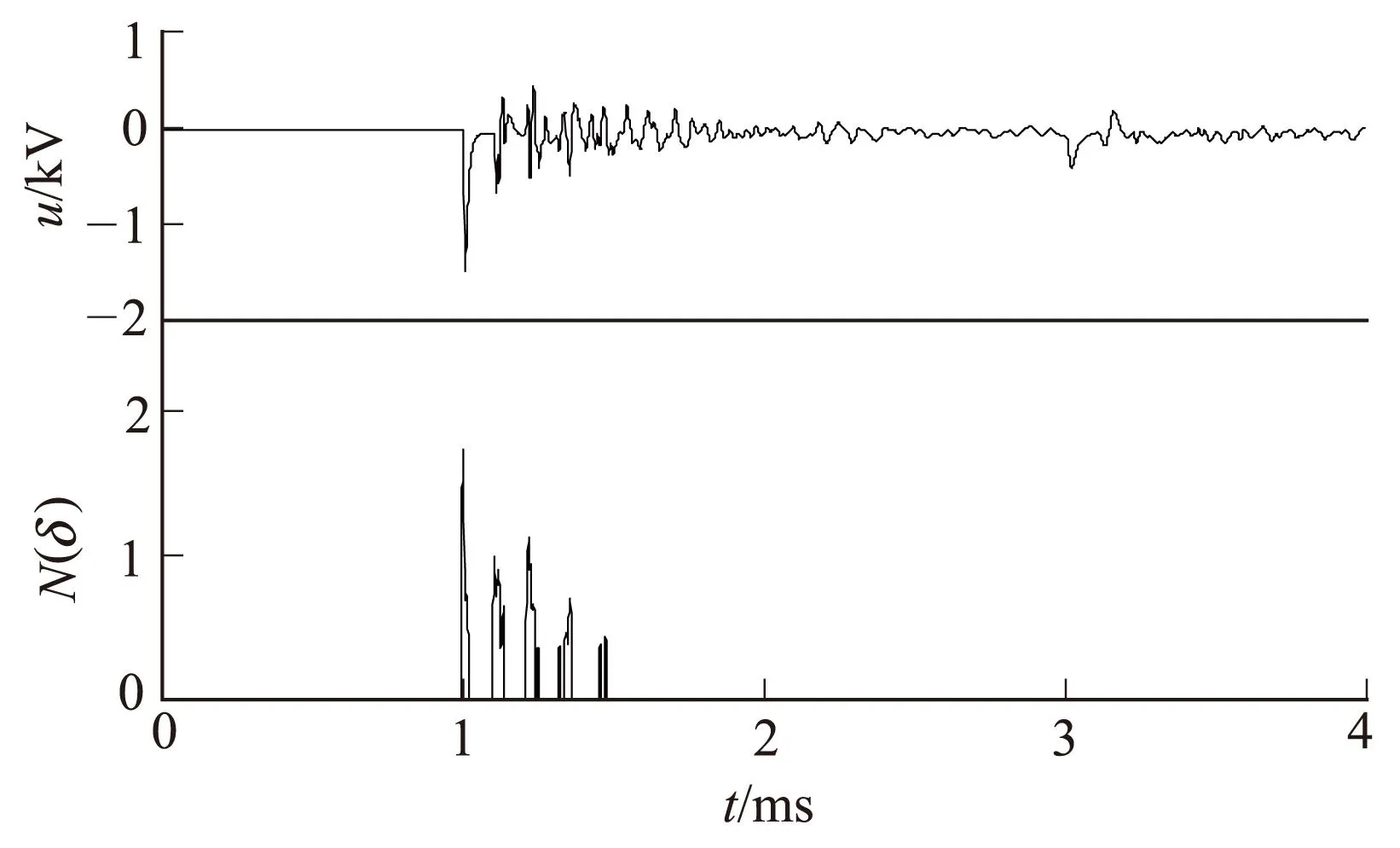
图1　原始行波信号及其网格分形奇异值提取结果

图1为利用上述方法对时长4 ms、采样频率为1 MHz的行波仿真信号进行分析的结果，其中u为原始行波电压瞬时值。由图1可得：原始行波波头与网格分形算法所得故障行波波头的到达时间均为1.002 ms，说明网格分形算法能准确、有效地识别出波头到达时间。

3三端式行波测距方法

当行波在一条均匀线路上传播时，其波速可视作恒定，则传输距离与传输时间成正比。基于该原理，本文提出三端式行波故障测距方法，以消除行波速度的影响。

3.1故障区间定位

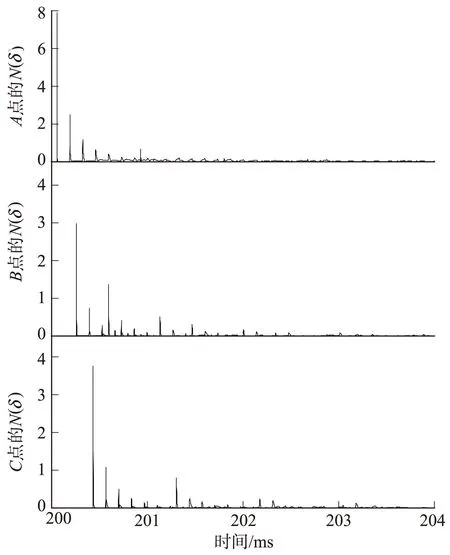
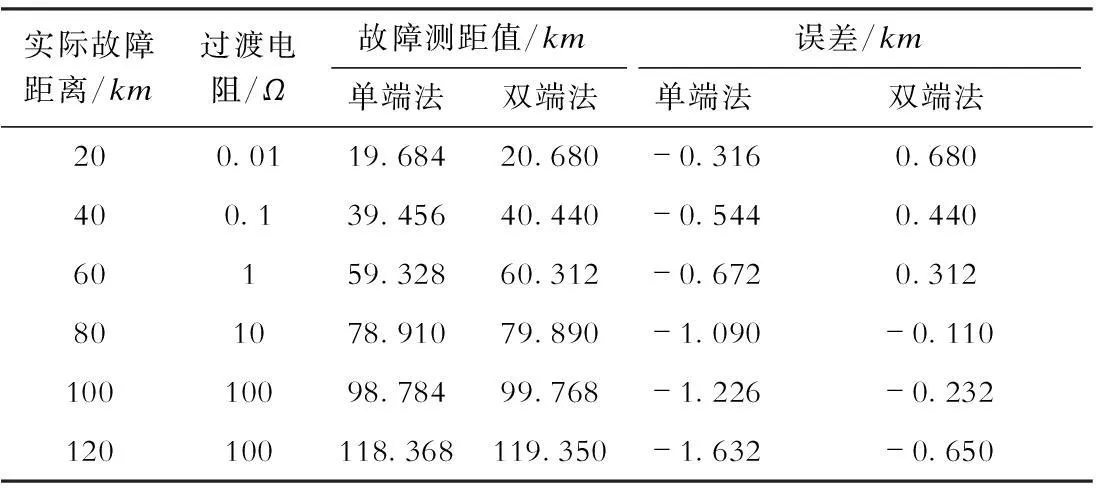
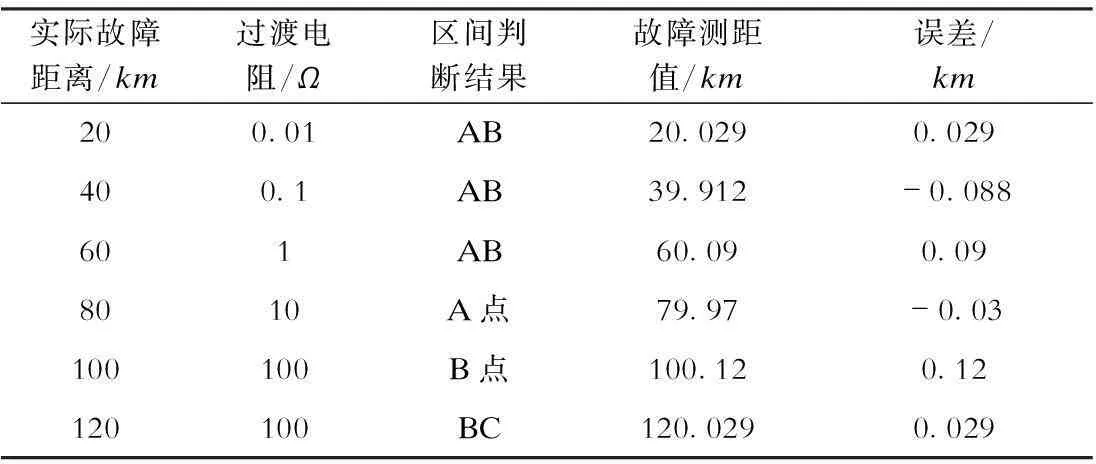
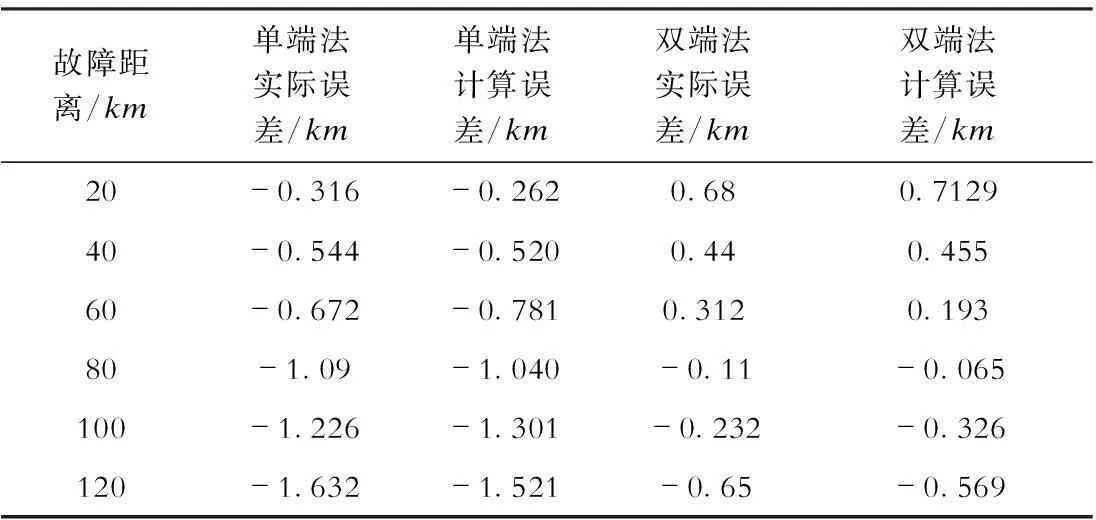
图2是三端式行波故障测距原理图。A、C两点为输电线路两端点，B为线路中间任意一点，设其距离C点xL(0

图2　三端式行波故障测距原理

3.2故障测距算法

如图2所示，若故障点F的位置变化，则A′点可位于AB区间或BC区间内，也可能在AC区间外侧。

当A′位于AB区间内时，根据几何关系可得

(3)

式中v为线路实际波速。

当A′位于BC区间或者AC区间外侧时，推导可得与式(3)相同的结论。

若故障发生在BC区间，则

考虑线路弧垂影响时，在杆塔基本均匀分布且弧垂形状相近的情况下，各段线路的长度可视为放大一定倍数α后的数值。由于推导过程中采用了比例法，可有效消除线路弧垂的影响，因此只需将测距结果乘以系数α，即可得到故障点距线路端点的长度。

4仿真结果分析

4.1仿真结果

在PSCAD/EMTDC软件中建立如图2结构的220 kV双端供电系统，并对其进行仿真分析。该输电线路全长150 km，分别在线路两端点A、C，以及距C点50 km处的B点设置行波检测点。

该输电线路采用分布参数模型，其参数为：正序电阻R1=0.035 Ω/km，正序电感L1=1.35 mH/km，正序电容C1=0.008 7 μF/km；零序电阻R0=0.3 Ω/km，零序电感L0=3.66 mH/km，零序电容C0=0.006 2 μF/km。

设定距离A点20 km处发生单相接地故障，接地电阻为0.01 Ω，仿真采样频率为1 MHz，仿真开始后0.2 s发生故障。3个检测点的电流线模行波信号的网格分形分析结果如图3所示。

图3　各检测点线模行波的网格分形分析结果

检测得A点初始行波到达时间为200.068 ms，B点初始行波到达时间为200.274 ms，C点初始行波到达时间为200.445 ms，取x=1/3，则

根据故障区段判定原则可判定故障位于AB区间，应用式(3)得到故障点F到端点A的距离s为20.029km，绝对误差为29m，测距精度较高。

根据线路正序参数可计算线模行波速度理论值为2.917×105km/s，在仿真条件下线模行波按照该速度在输电线路上传播。若设定波速为2.89×105km/s，即与实际波速相差1%，则单端法的故障测距结果为19.684km，绝对误差为316m；双端法的故障测距结果为20.68km，绝对误差为680m。两者误差均远大于三端法。

改变实际故障距离与过渡电阻以设置不同的故障工况，应用单端法和双端法进行故障测距，仿真试验结果见表1。

表1单端法和双端法的故障测距结果

实际故障距离/km过渡电阻/Ω故障测距值/km单端法双端法误差/km单端法双端法200.0119.68420.680-0.3160.680400.139.45640.440-0.5440.44060159.32860.312-0.6720.312801078.91079.890-1.090-0.11010010098.78499.768-1.226-0.232120100118.368119.350-1.632-0.650

由表1可见，当预设的行波速度与实际波速不一致时，单端法与双端法均会出现较大误差。单端法的测距误差随故障点到测量端的距离增大而增大，双端法的测距误差则随故障点到线路中点的距离增大而增大，计算结果与式(1)和式(2)的分析结果一致。

应用本文提出的三端式行波故障测距原理对不同故障工况进行故障测距，仿真试验结果见表2。

由表2可知，应用本文提出的三端式故障测距原理进行故障测距的绝对误差仅为几十米，远小于单端法与双端法的测距结果，验证了该方法可有效消除线路行波速度对测距结果的影响，从而准确判断故障位置。同时，三端式故障测距原理只需检测初始行波波头，无需考虑行波折反射，有效消除了反射波识别带来的误差。

表2　三端法的故障测距结果

4.2误差分析

将利用仿真试验得到的初始行波到达时间分别代入式(1)和式(2)，求取单端法及双端法的计算误差值，并与测距误差进行对比，其结果见表3。

表3误差比较

故障距离/km单端法实际误差/km单端法计算误差/km双端法实际误差/km双端法计算误差/km20-0.316-0.2620.680.712940-0.544-0.5200.440.45560-0.672-0.7810.3120.19380-1.09-1.040-0.11-0.065100-1.226-1.301-0.232-0.326120-1.632-1.521-0.65-0.569

由表3可见，无论是单端法还是双端法，其实际测距误差与理论计算得到的测距误差较为接近，但并不相等，这是由于检测到的行波到达时刻与实际行波到达时刻间的误差所致。本文行波采样频率为1MHz，因此存在着最大为0.5μs的时间误差。由于三端式测距算法消除了行波速度的影响，其测距误差主要来源于时间误差，可通过提高采样频率予以减小。

在实际应用中，还要考虑行波测距装置的同步误差。目前，全球定位系统的时间同步精度已达到微秒级，在该精度下本文提出的三端式测距算法能保持较高的测距精度，且线路越长测距精度越高。

5结论

a)分析了行波速度不确定性及其对现有故障测距方法的影响，并通过仿真试验进行验证。结果表明，当设定的波速与实际波速不一致时，单端法及双端法均会出现较大的误差。

b)所提出的基于网格变化规律的行波波头提取方法能精确、有效地识别行波波头的到达时刻，为三端式测距算法提供了依据。

c)所提出的三端式行波测距方法只需检测初始行波波头，能有效消除波速不确定性所带来的测距误差，大大提高了测距精度。

d)行波采样频率与时间同步精度会对本文提出的方法造成一定的影响，该误差属于固有误差，可通过提高硬件性能给予消除。

参考文献：

[1] 陈平，徐丙垠，李京，等. 现代行波故障测距装置及其运行经验[J]. 电力系统自动化, 2003, 27(6):66-69.

CHENPing,XUBingyin,LIJing,etal.ModernTravellingWaveBasedFaultLocatorandItsOperatingExperience[J].AutomationofElectricPowerSystem, 2003，27(6):66-69.

[2] 李雪云，刘青，李丽英. 基于单端行波法的配电网混合线路波头组合式故障测距方法[J]. 华北电力大学学报(自然科学版)，2014, 41(5):55-60.

LIXueyun,LIUQing,LILiying.BasedonSingle-endedTravellingWaveaHeadCombinedFaultLocationMethodAboutDistributionNetworktheHybrid[J].JournalofNorthChinaElectricPowerUniversity(NaturalScienceEdition), 2014, 41(5):55-60.

[3] 季涛，孙同景，徐丙垠, 等. 配电混合线路双端行波故障测距技术[J].中国电机工程学报,2006, 26(12):89-94.

JITao,SUNTongjing,XUBingyin,etal.StudyonFaultLocationofDistributionMixedFeedersBasedonDoubleTerminalMethodofTravellingWaves[J].ProceedingsoftheCSEE, 2006, 26(12):89-94.

[4] 李泽文，曾祥君，徐晓菁，等.输电线路双端行波故障定位新算法[J]. 电力系统自动化，2006，30(15):40-43.

LIZewen,ZENGXiangjun,XUXiaojing,etal.NewFaultLocationAlgorithmBasedonDoubleTerminalTravellingWavesforTransmissionlines[J].AutomationofElectricPowerSystems, 2006, 30(15):40-43.

[5] 刘亚东，盛戈皞，王葵，等. 输电线路分布式综合故障定位方法及其仿真分析[J].高电压技术，2011，37(4):923-929.

LIUYadong,SHENGGehao,WANGKui,etal.MethodandSimulationAnalysisofComprehensivelyDistributedFaultLocationofTransmissionLine[J].HighVoltageEngineering, 2011, 37(4):923-929.

[6] 黄雄，王志华，尹项根，等. 高压输电线路行波测距的行波波速确定方法[J]. 电网技术, 2004, 28(19):34-37.

HUANGXiong,WANGZhihua,YINXianggen,etal.TravellingWaveVelocityMeasurementinFaultLocationBasedonTravellingWaveforHighVoltageTransmissionLine[J].PowerSystemTechnology, 2004, 28(19):34-37.

[7] 尹晓光，宋琳琳，尤志,等.与波速无关的输电线路双端行波故障测距研究[J]. 电力系统保护与控制, 2011, 39(1):35-39.

YINXiaoguang,SONGLinlin,YOUZhi,etal.StudyofFaultLocatingforTransmissionLineDoubleTerminalTravellingWavesUnrelatedtoWaveSpeed[J].PowerSystemProtectionandControl, 2011, 39(1):35-39.

[8] 张峰，梁军，张利，等. 基于三端行波测量数据的输电线路故障测距新方法[J]. 电力系统自动化，2008，32(8):69-72.

ZHANGFeng,LIANGJun,ZHANGLi,etal.NovelMethodAboutTravellingWaveFaultLocationBasedonTrebleTerminalMeasurementDataforTransmissionLines[J].AutomationofElectricPowerSystems, 2008, 32(8):69-72.

[9] 张小飞，徐大专，齐泽峰，等. 基于分形的奇异信号的检测[J]. 南京航空航天大学学报, 2003, 35(4):404-408.

ZHANGXiaofei,XUDazhuan,QIZefeng,etal.DetectionofSingularSignalBasedonFractalTechnique[J].JournalofNanjingUniversityofAeronautics&Astronautics, 2003, 35(4):404-408.

Three-terminal Fault Location Method for Travelling Wave RemovingInfluenceofWaveVelocity

CUI Hao1, WANG Fenghua2, MU Ka2, ZHANG Jun2, LIU Yadong2

(1.FengxianPowerSupplyBranchCompany,StateGridShanghaiMunicipalElectricPowerCompany,Shanghai201400,China; 2.KeyLaboratoryofControlofPowerTransmissionandConversion(ShanghaiJiaotongUniversity),MinistryofEducation,Shanghai200240,China

Abstract：Inordertoimproveveracityoftravellingwavebasedfaultlocationmethodforpowertransmissionlines,akindofthree-terminalfaultlocationalgorithmremovinginfluenceofwavevelocityispresentedonthebasisofanalyzingdistance-measuringerrorcausedforreasonofuncertaintyofwavevelocity.Threetravellingwavefaultlocationdeviceswithtimesynchronousmodulesareinstalledrespectivelyatbothterminalsandanylocationinthemiddlesegmentoftheline,andgrillefractalalgorithmisappliedtoextractarrivaltimeofinitialtravellingwaveatthetimeoflinefault.Basedonproportionalrelationshipoftransmissiondistanceandtimeoftravellingwave,faultlocationformulaabouttimeoffaultinitialtravellingwavereachingtoeachmeasuringpointisestablished.Boththeoreticalanalysisandsimulatedresultsindicatethatthismethodisnotaffectedbytransmissionvelocityoftravellingwaveandisabletoeffectivelyimproveveracityoffaultlocationofpowertransmissionlines.

Keywords：faultlocation;three-terminal;travellingwave;grillefractalalgorithm

收稿日期：2016-03-22

基金项目：国家自然科学基金资助项目(51307109)

doi:10.3969/j.issn.1007-290X.2016.06.018

中图分类号：TM614

文献标志码：A

文章编号：1007-290X(2016)06-0098-06

作者简介：

崔浩(1981)，男，上海人。工程师，工学硕士，主要研究方向为配电网继电保护与控制。

王丰华(1973)，女，河南洛阳人。副教授，工学博士，主要研究方向为电力系统故障检测。

穆卡(1995)，男，河北邢台人。在读硕士研究生，主要研究方向为电力系统故障检测。

(编辑李丽娟)