基于模型预测控制的互联电网阻尼控制

段洁，孙正龙，张秀琦

(东北电力大学 电气工程学院，吉林 吉林 132012)



基于模型预测控制的互联电网阻尼控制

段洁，孙正龙，张秀琦

(东北电力大学 电气工程学院，吉林 吉林 132012)

摘要：针对同步发电机电压调节和阻尼改善之间的矛盾，提出一种新的方法来处理多机电力系统中电力系统稳定器(power system stabilizer，PSS)和自动电压调节器(automatic voltage regulator，AVR)的鲁棒协调问题。该方法将模型预测控制(model predictive control，MPC)应用到励磁调节器中，提高了AVR和PSS的鲁棒性。建立多机系统线性化模型，通过模型预测和优化求解，得到励磁控制器的最优控制输入。利用MATLAB/Simulink对典型的“4机2区”电力系统进行测试，仿真结果表明基于MPC的鲁棒协调AVR+PSS方式的控制器可以在保持良好稳态电压调节精度的情况下，增加系统阻尼特性，提高系统动态稳定水平。

关键词：阻尼控制；模型预测控制；电力系统稳定器；自动电压调节器；低频振荡

随着互联电力系统规模的不断扩大及大型机组快速励磁系统的应用，低频振荡问题日益突出，互联电网的区间弱阻尼振荡已经成为制约中国区域电网间功率交换能力的主要瓶颈。改变网络结构能够根治低频振荡问题，但投资高。从经济可行性考虑，一般选择二次设备来提高系统的阻尼特性，目前使用最广泛的控制方法是自动电压调节器-电力系统稳定器(automatic voltage regulator/power system stabilizer，AVR+PSS)控制模式。传统的AVR+PSS控制模式是序贯设计，AVR需满足所需的电压调节特性，PSS需满足所需的阻尼特性。两种策略都通过直轴励磁来实施，AVR调节无功功率，PSS调节有功功率，但这两个目标是不可能同时实现的[1]。近年来，国内外学者对于AVR和PSS的综合设计提出了多种实用化方法，如自适应控制[2]、极点配置[3]、鲁棒控制[4]等。为解决电压调节和阻尼改善之间的协调性问题，文献[5]采用不敏感控制理论，在励磁系统中设计了一个状态反馈控制器；文献[6]采用改进的线性矩阵不等式方法来最优化控制器参数。

模型预测控制(model predictive control，MPC)是一种广泛应用于过程控制的先进控制方法[7]，其根据当前系统的测量信息，通过某一最优性能指标来确定当前的控制动作，具有很强的预见性，控制效果优于经典反馈控制[8]。MPC因具有建模易、响应速度快且鲁棒性好等特点而被应用于电力系统的诸多方面，如热过载紧急控制[9]、系统电压稳定性的改善[10]和电力系统阻尼控制[11]。文献[12]用自适应模型预测控制器替代传统的AVR和PSS，可有效抑制电力系统低频振荡，但对象是单机无穷大系统模型。

本文将MPC应用到励磁调节器中，研究基于MPC的鲁棒协调AVR+PSS阻尼控制器的设计方法。

1多机电力系统线性化模型

对于多机电力系统，采用小干扰线性化模型，线性化时忽略励磁参考电压的变化。系统的数学模型为[13]：

(1)

式中：δ为发电机转子角；ω0为同步角速度；ω为同步发电机的角速度；M为发电机的惯性时间常数；Pm为机械功率，小扰动分析时ΔPm=0；Pe为发电机电磁功率；D为阻尼系数；E′q为同步发电机q轴暂态电动势；T′d0为d轴开路暂态时间常数；Ufd为励磁绕组电压；Us为PSS的输出电压；Ut为发电机端电压；TA、KA分别为励磁系统综合放大环节的时间常数和增益；xd为d轴同步电抗；x′d为d轴暂态电抗；xq为q轴同步电抗；Ud和Uq分别为定子的d轴和q轴绕组电压；Id和Iq分别为定子的d轴和q轴绕组电流。

2模型预测阻尼控制

2.1预测方程

在设计模型预测控制器的过程中，需对线性化模型进行离散化处理[14]。为了更精确地调节机端电压，选取的系统状态变量为发电机的电磁功率、机端电压以及角速度偏差，则式(1)所描述的系统可写成状态空间形式[4]。其表达式为：

(2)

式中：x、u和y分别为系统的状态、输入和输出变量，t为时间，Ac、Bc和Cc分别为系统状态矩阵、控制矩阵和观测矩阵。

将式(2)离散化，得：

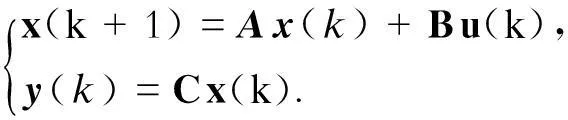
(3)

其中：

式中：k为采样时刻，Ts为采样周期，τ为时间。

首先根据MPC算法原理[14]，设定预测时域为Np，控制时域为Nc，且Nc≤Np；然后根据系统当前时刻(即k时刻)的状态信息x(k+1)及状态方程(3)，在有限时域内对系统未来输出变量y(k+Np|k)进行预测。其表达式为：

(4)

定义Np步预测输出向量Y和Nc步输入向量U如下：

则Np步预测输出向量

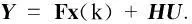
(5)

其中：

2.2目标函数及其约束条件

MPC的机理为：在每一个采样时刻，根据获得的当前测量信息，在线求解一个有限时域内的开环优化问题，并将得到的控制序列的第一个元素作用于被控对象，在下一采样时刻重复上述过程，用新的测量值刷新优化问题并重新求解[15]。从函数依赖关系可知，所得的优化解是当前测量值的函数，是一个反馈控制律。可见，通过滚动优化的机制得到最优控制的一个闭环解，通过在线校正构成具有负反馈环节的系统，大大提高了预测控制系统的鲁棒性。

在每一个采样时刻k，MPC的二次目标函数和约束条件为：

(6)

式中：J为目标函数，Yr为预测时域内的参考输入，Q为输出加权矩阵，R为控制加权矩阵，umin为输入信号的最小值，umax为输入信号的最大值。

将式(5)代入式(6)得：

(7)

式(7)构成了二次规划问题，采用矩阵实验室(Matrix Laboratory，MATLAB)中的Quadprog函数求解，运用滚动优化策略，取最优控制序列的第一个元素作为系统实际控制动作。

2.3控制系统的结构

基于MPC的鲁棒协调AVR+PSS控制方式下的励磁系统如图1所示。

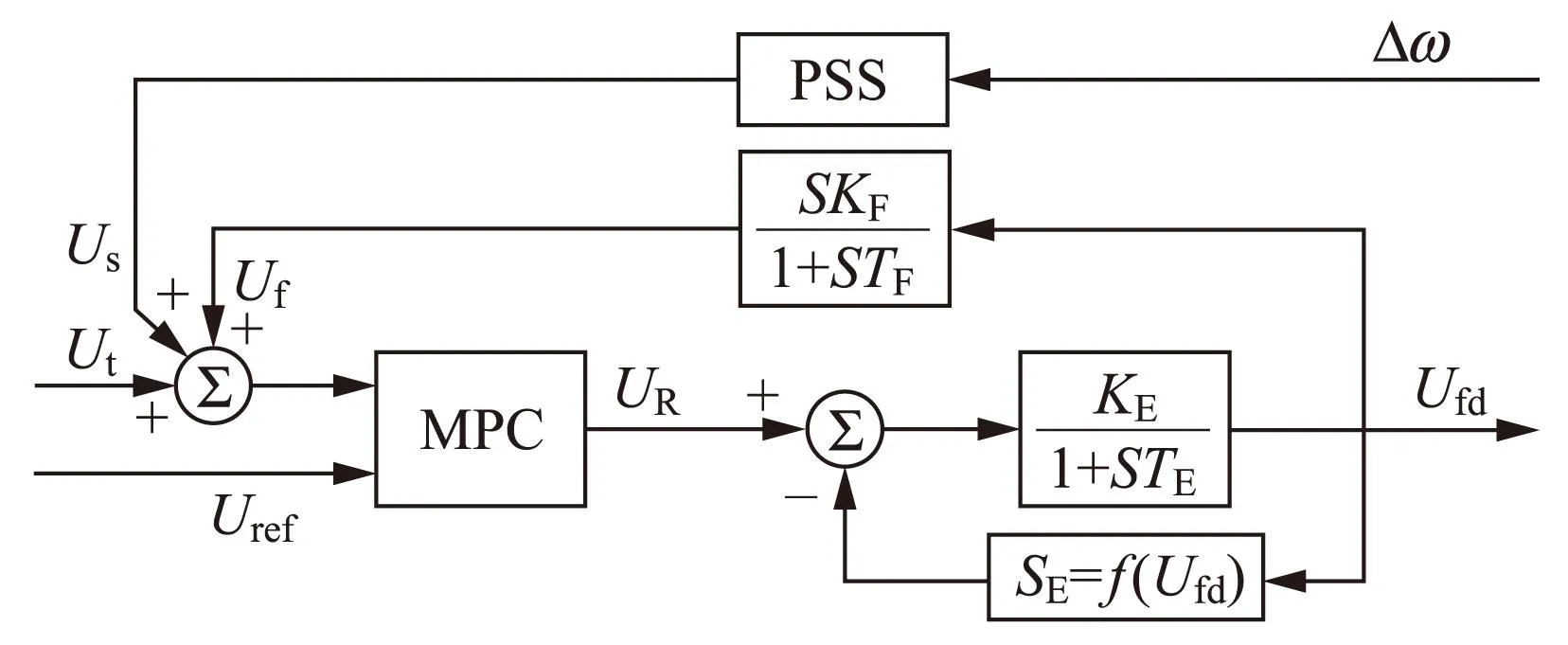
Uf—补偿器电压，Uref—励磁参考电压，UR—MPC的输出电压，S—复频率，SE—励磁机的饱和系数，KE—励磁机的自励系数，KF—转子软反馈环节的增益，TF—转子软反馈环节的时间常数，TE—励磁机时间常数，f—函数。图1　含MPC的励磁系统模型

为了实现电压调节和阻尼改善之间的协调控制，在该励磁系统中，用鲁棒性好、响应速度快的MPC替代传统的AVR，形成鲁棒AVR，并采用多频带电力系统稳定器(multi band power system stabilizer，MB-PSS)作为发电机励磁附加控制，其输入信号为同步发电机的角速度偏差Δω。将发电机端电压Ut、PSS的输出电压Us和补偿器电压Uf叠加后作为MPC的输入信号，励磁参考电压Uref为MPC的参考输入，同时MPC的输出信号UR作用于发电机的励磁器。

3仿真算例

采用“4机2区”电力系统(如图2所示)，在MATLAB/Simulink中搭建此电力系统模型，系统参数见文献[16]。区域1的负荷为967 MW，区域2的负荷为1 767 MW。

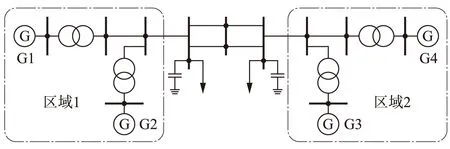
图2　“4机2区”电力系统

在未安装PSS时，对该“4机2区”系统进行特征值分析，计算出2个本地模式和1个区间模式的参与因子，结果见表1。

表1各振荡模式的发电机参与因子

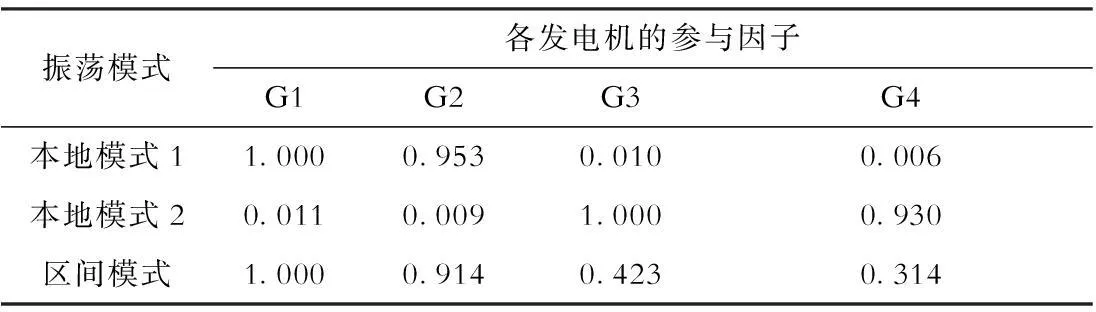
振荡模式各发电机的参与因子G1G2G3G4本地模式11.0000.9530.0100.006本地模式20.0110.0091.0000.930区间模式1.0000.9140.4230.314

根据得到的参与因子大小，确定在G1和G3上安装基于MPC的鲁棒协调AVR+PSS阻尼控制器，抑制系统低频振荡。在Simulink中搭建此系统模型，设系统输入量u为励磁机输入电压，输出量y为发电机端电压、补偿器电压以及PSS的输出电压，用linmod命令求出系统的状态模型(Ac、Bc、Cc)，在此基础上计算和更新控制量u(k)。依据MPC参数选取的一般原则[17]，确定仿真中模型预测控制器的相关参数如下：离散时间步长 Δt=0.1 s，输出权重矩阵Q= 1×INp×Np，控制权重矩阵R= 0.1×INu×Nu，控制时域Nu=3，预测时域Np=15，-0.9≤u≤1.1。

扰动方式：在t=1 s时联络线中间发生三相短路故障，0.2 s后故障清除。为了说明本文所提控制策略的有效性，对装设基于MPC的鲁棒协调AVR+PSS控制器、传统的AVR+Delta w-PSS控制器和AVR+MB-PSS控制器的控制效果进行对比，图3、图4和图5分别为瞬时故障下G1相对于G4的功率因数角δ14、联络线有功功率P和G1机端电压Ut1的振荡曲线。

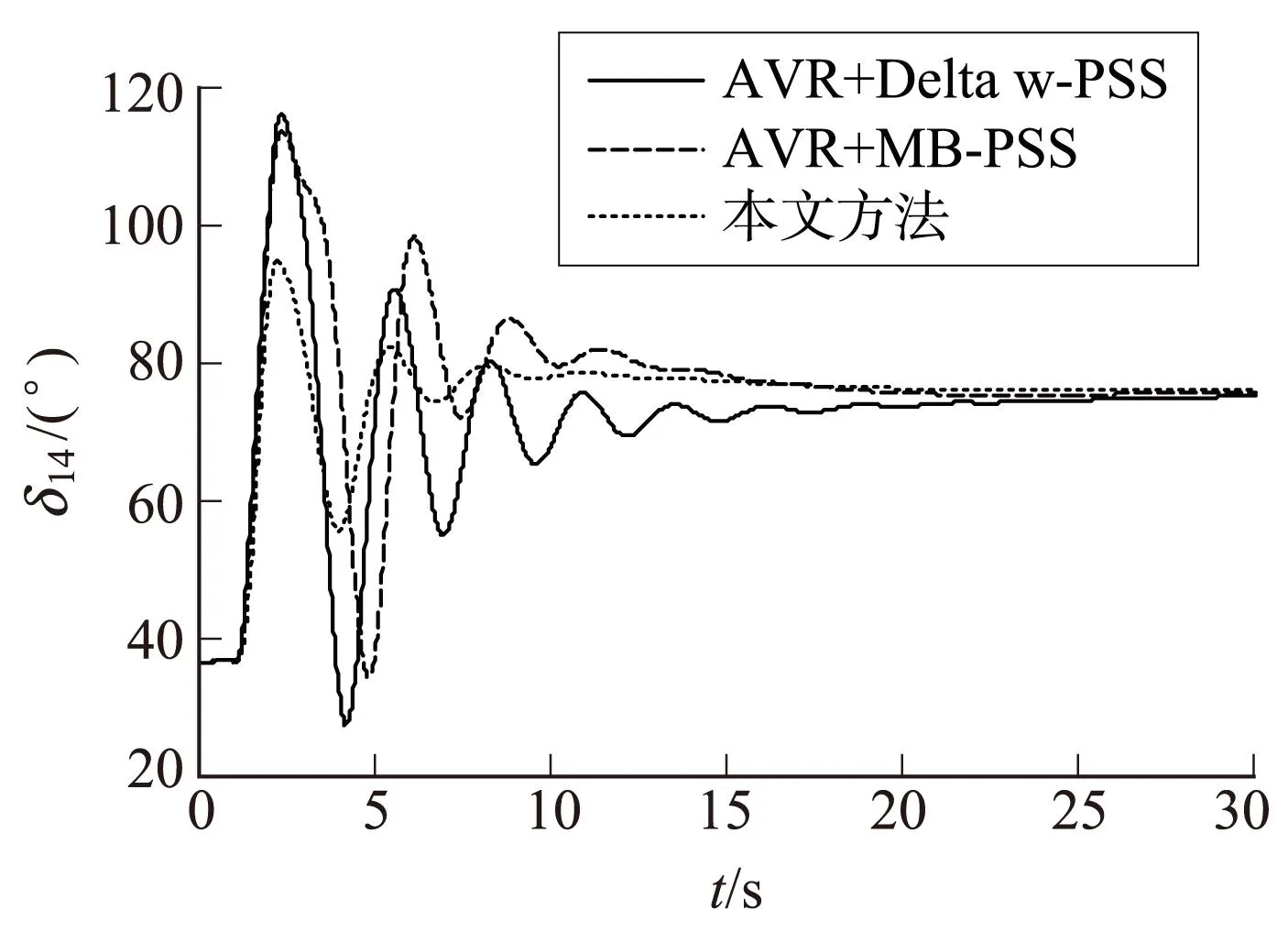
图3　G1相对于G4的功率因数角曲线

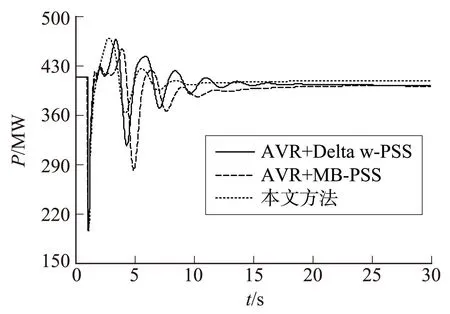
图4　联络线有功功率振荡曲线

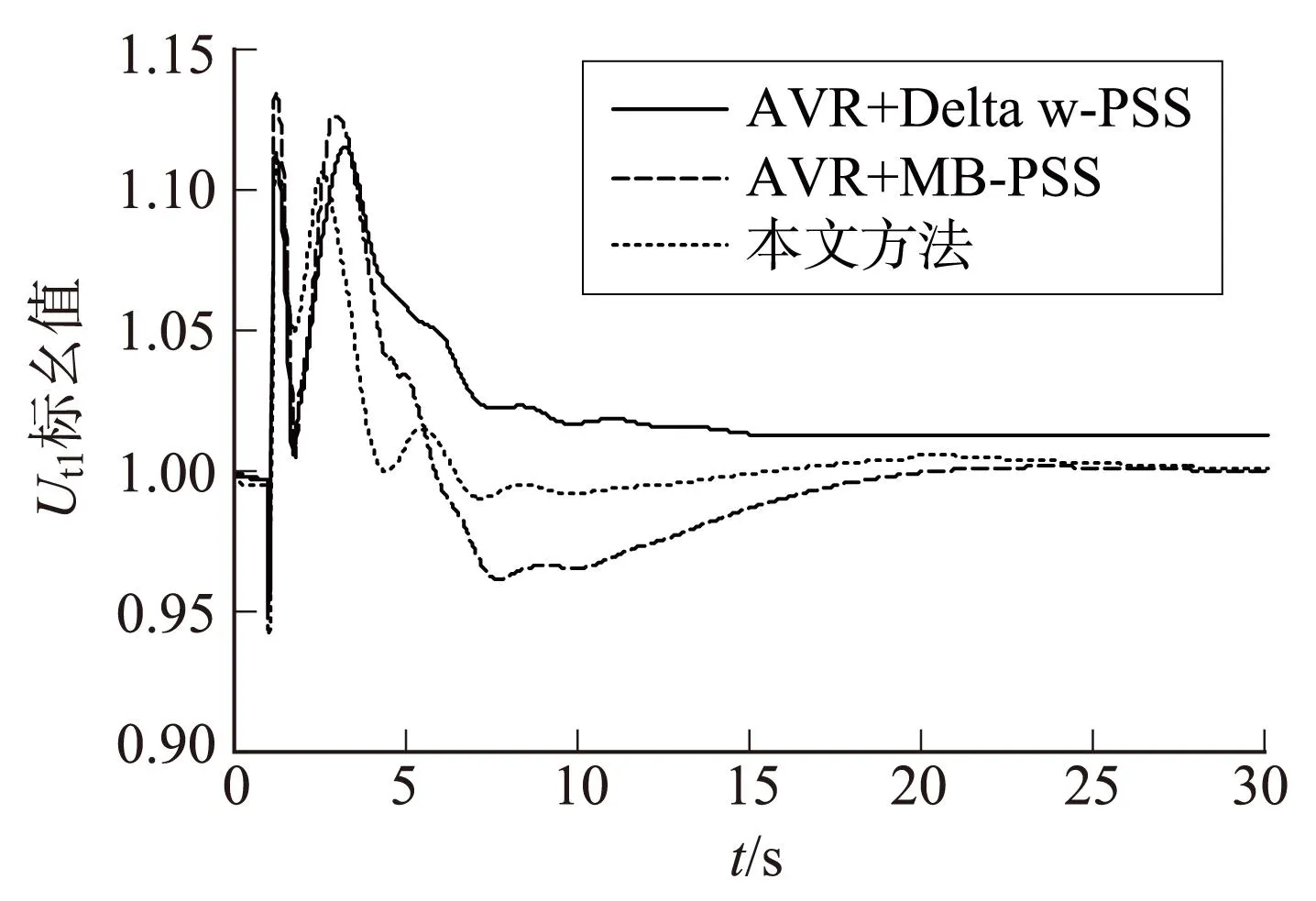
图5　G1机端电压曲线

从图3至图5可以看出：与传统的AVR+Delta w-PSS方式相比，传统的AVR+MB-PSS方式和本文方法均提高了系统的动态稳定性能，但本文方法的发电机功率因数角和联络线有功功率的振荡更小，衰减更快，性能更好；本文方法可以使机端电压快速地恢复到扰动前的值，传统的AVR+MB-PSS控制方式虽然也能使机端电压恢复至扰动前的值，但机端电压出现了较大的波动，而采用传统的AVR+Delta w-PSS控制方式时机端电压偏离了参考值。

4结论

本文设计了一种基于MPC的鲁棒协调AVR+PSS控制器。该控制器利用MPC建模易、鲁棒性好、响应速度快的特点，有效解决了电压调节和阻尼改善之间的固有矛盾。以“4机2区”电力系统为例进行仿真分析，结果表明该控制器可以在保持良好稳态电压调节精度的前提下，增加系统阻尼特性，提高了系统动态稳定水平。

参考文献：

[1] LAW K，HILL D.Robust Controller Structure for Coordinated Power System Voltage Regulator and Stabilizer Design[J].IEEE Transactions on Control Systems Technology，1994，2(3)：220-232.

[2] FUSCO G，RUSSO M.Adaptive Voltage Regulator Design for Synchronous Generator[J].IEEE Trans. on Energy Conversion，2008，23(3)：946-956.

[3] 马晓峰，赵书强，顾雪平.基于输出反馈和区域极点配置的电力系统阻尼控制器研究[J].电工技术学报，2011，26(4)：175-184.

MA Xiaofeng，ZHAO Shuqiang，GU Xueping.Research on Power System Damping Controllers Based on Output Feedback and Region Poles Assignment[J].Transactions of China Electrotechnical Society，2011，26(4)：175-184.

[4] 阮阳，袁荣湘，万黎，等.同步发电机的非线性鲁棒电压控制[J].电工技术学报，2012，27(9)：9-16.

RUAN Yang，YUAN Rongxiang，WAN Li，et al. Nonlinear Robust Voltage Control for Synchronous Generators[J].Transactions of China Electrotechnical Society，2012，27(9)：9-16.

[5] BOURLES H，PERES S.Analysis and Design of a Robust Coordinated AVR/PSS[J].IEEE Transactions on Power Systems，1998，13(2)：568-575.

[6] BEVRANI H，HIYAMA T.Stability and Voltage Regulation Enhancement Using an Optimal Gain Vector[C]//2006 IEEE Power Engineering Society General Meeting，June 18-22,2006,Montreal,Canada. Piscataway：IEEE，2006：1-6.

[7] QIN S，BADGWELL T.A Survey of Industrial Model Predictive Control Technology[J].Control Engineering Practice，2003，11(6)：733-764.

[8] 刘向杰，孔小兵.电力工业复杂系统模型预测控制：现状与发展[J].中国电机工程学报，2013，33(5)：79-85.

LIU XiangJie，KONG Xiaobing.Present Situation and Prospect of Model Predictive Control Application in Complex Power Industrial Process[J].Proceedings of the CSEE，2013，33(5)：79-85.

[9] OTOMEGA B，GLAVIC M.Emergency Alleviation of Thermal Overloads Using Model Predictive Control[C]//2007 IEEE Lausanne Power Tech，July 1-5,2007, Lausanne,Switzerland. Piscataway：IEEE，2007：201-206.

[10] HISKENS I A，GONG B.Voltage Stability Enhancement Via Model Predictive Control of Load[J].Intelligent Automation Soft Computation，2006，12(1)：117-124.

[11] 叶华，刘玉田.基于在线递推闭环子空间辨识的模型预测阻尼控制[J].中国电机工程学报，2009，29(28)：55-61.

YE Hua，LIU Yutian.Model Predictive Damping Control Based on On-line Recursive Closed-loop Subspace Identification [J].Proceedings of the CSEE，2009，29(28)：55-61.

[12] LIN W，CHEUNG H.Model Prediction Adaptive Control for Wide-Area Power System Stability Enhancement[C]//2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century，July 20-24,2008,Pittsburgh,Pennsylvania. Piscataway：IEEE，2008：1-8.

[13] 王成山，石颉.考虑时间延迟影响的电力系统稳定器设计[J].中国电机工程学报，2007，27(10)：1-6.

WANG Chengshan，SHI Jie.PSS Designing with Consideration of Time Delay Impact [J].Proceedings of the CSEE，2007，27(10)：1-6.

[14] 陈虹.模型预测控制[M].北京：科学出版社，2013：15-30.

[15] 平续斌，丁宝苍.动态输出反馈鲁棒模型预测控制[J].自动化学报，2012，38(1)：31-37.

PING Xubin，DING Baocang.Dynamic Output Feedback Robust Model Predictive Control[J].Acta Automatica Sinica，2012，38(1)：31-37.

[16] KUNDUR P.电力系统稳定与控制[M].北京：中国电力出版社，2002：813-816.

[17] 赵可君.模型预测控制的参数优化[D].厦门：厦门大学，2013.

Damping Control for Interconnected Power Grid Based on Model Predictive Control

DUAN Jie, SUN Zhenglong, ZHANG Xiuqi

(Electrical Engineering College of Northeast Dianli University, Jilin, Jilin 132012, China)

Abstract：In allusion to conflict between voltage regulation and damping improvement for synchronous generator, a kind of new method for dealing with robust coordination between power system stabilizer (PSS) and automatic voltage regulator (AVR) of multi-machine power system is presented which applies model predictive control (MPC) in excitation regulator and improves robust of AVR and PSS. Linear model for multi-machine system is established for model prediction and optimization solution and it is able to obtain the optimal control input of the excitation controller. MATLAB/Simulink is used for testing typical two-area four-machine power system and simulation results indicate that the robust AVR+PSS controller based on MPC is able to increase damping performance and improve dynamic stability of the system in the case of keeping good regulation precision of steady-state voltage.

Key words：damping control; model predictive control; power system stabilizer; automatic voltage regulator; low frequency oscillation

收稿日期：2016-01-05修回日期：2016-03-04

doi:10.3969/j.issn.1007-290X.2016.06.014

中图分类号：TM712

文献标志码：A

文章编号：1007-290X(2016)06-0078-04

作者简介：

段洁(1991)，女，湖北荆门人。在读硕士研究生，研究方向为电力系统稳定与控制。

孙正龙(1988)，男，吉林省吉林市人。在读博士研究生，研究方向为电力系统稳定性分析及大规模可再生能源并网。

张秀琦(1992)，女，吉林省吉林市人。在读硕士研究生，研究方向为电力系统稳定与控制。

(编辑李丽娟)