基于改进型DOB的电液伺服力控制技术研究
2016-07-16吕晓娟
吕晓娟
(郑州电力高等专科学校,河南 郑州 451450)
基于改进型DOB的电液伺服力控制技术研究
吕晓娟
(郑州电力高等专科学校,河南 郑州451450)
摘要:考虑到电液伺服力控制系统容易受到外界载荷扰动影响等问题,提出了一种基于改进型DOB算法的电液伺服力控制器。通过对控制系统中的标称控制器P,低通的滤波器K以及控制参数V进行设计,以消除电液伺服力控制系统受到外界扰动信号d和电液伺服力控制系统测量的噪声信号n对系统的影响,提高DOB系统的鲁棒性能。通过仿真试验验证提出的改进型DOB算法对提高电液伺服力控制系统稳定性和抗干扰能力的效果,并与基于模糊算法和基于常规DOB算法的控制系统进行比较。结果表明,提出的改进型DOB算法使得电液伺服力控制系统具有更好的鲁棒性以及稳定性。
关键词:电液伺服;压力控制;模糊算法;扰动观测器
0 引言
电液伺服控制系统因其具有重量小、控制精度高、静动态特性较好、体积小巧、使用寿命长以及功率重量比和力矩重量比较大等优点,使得电液伺服控制系统无论是在军事领域、工业领域还是民用领域都得到了极其广泛的应用[1]。
文献[2]中对疲劳试验机的电液伺服力控制系统进行了研究,主要使用模糊算法和自适应学习算法相结合建立控制系统。文献[3]中将滑模变结构控制理论与自适应控制理论相结合,对电液伺服力控制系统进行控制研究。文献[4]中使用模糊学习算法对电液伺服力控制系统进行研究,以提高控制系统的鲁棒性能。文献[5]中对电液伺服力控制系统的多余力矩抑制问题进行了研究,使用神经网络控制算法设计控制器,以解决电液伺服加载模拟系统的非线性等问题。
本文对电液伺服力控制系统进行研究,主要研究控制系统对外界负载扰动的抗干扰能力以及稳定性。
1 电液伺服力控制数学模型
本文研究的电液伺服力控制系统主要是通过调整电液伺服阀控制电流的变化,从而控制电液伺服阀的输出,实现对液压油缸输出力的精确控制。
电液伺服力控制系统简图如图1所示。电液伺服力控制系统主要包含了电液伺服阀、单作用液压缸以及液压缸负载等。电液伺服力控制器将控制信号传递到伺服阀电磁铁中,伺服阀电磁铁将电信号转换为机械信号,控制伺服阀的先导阀动作,从而实现伺服阀阀芯的运动,实现电液伺服力的控制。
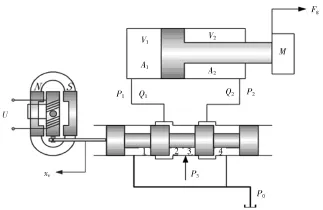
图1 电液伺服力控制系统简图
电液伺服阀控制非对称液压油缸的三个重要方程,即电液伺服阀流量方程、液压缸流量方程以及液压缸的力平衡方程。
(1)电液伺服阀流量方程为:

式中:xv为伺服阀芯位移(单位:m);PL为负载的压力(单位:N);Kq为流量增益(单位:m2/s);Kc为流量压力系数(单位:m3/s·Pa)。
(2)液压油缸的流量方程为:
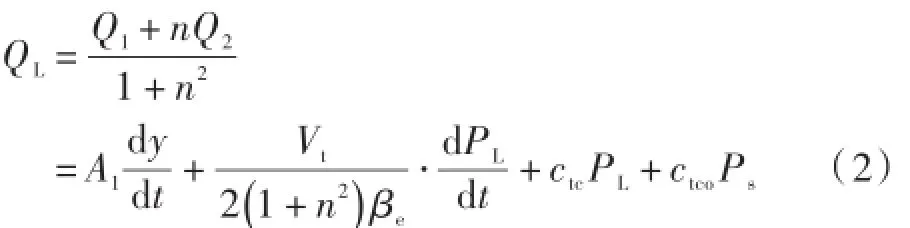
式中:A1为液压油缸无杆腔面积(单位:m2);βe为液压油液的弹性模数(单位:Pa);n为有效面积比;Q1为液压油缸无杆腔流量(单位:m3/s);Q2为液压油缸有杆腔流量(单位:m3/s)。
(3)液压油缸负载力平衡方程为:
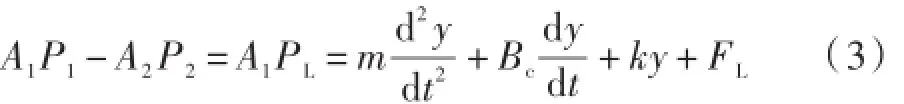
式中:k为负载的弹簧刚度(单位:N/m);FL为外负载力(单位:N);A2为液压油缸有杆腔面积(单位:m2);m为等效质量之和(单位:kg);Bc为粘性阻尼系数(单位:N·s/m)。
对电液伺服阀流量方程、液压油缸流量方程以及力平衡方程进行拉普拉斯变换,即可得到电液伺服力控制系统的传递函数:
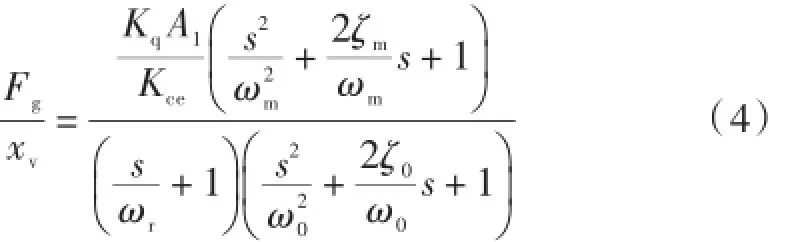
式中:ωr是转折频率(单位:Hz),是机械固有频率(单位:Hz);ω0为液压与机械总体固有频率(单位:Hz),为机械阻尼系数(单位:N·s/m),为液压与机械阻尼系数(单位:N·s/m),是系统总体压力增益(单位:为液压油缸负载力[5]单位:N)。
2 扰动力消除控制方法研究
目前,对于电液伺服力控制系统的负载扰动抑制控制方法有多种算法,本文主要针对基于模糊控制算法和基于DOB算法进行研究。
2.1基于模糊控制的方法
由于液压油缸工作时,环境和负载会时时变化,且液压系统的本身具有非线性特性,控制系统的参数必然会发生波动,采用传统的PID算法控制油液系统的全过程,其控制性能必然会受到影响。为了使得电液伺服力控制系统的输出能够快速稳定地跟踪预期值,将模糊控制与传统PID结合,利用模糊推理的策略,根据不同的偏差、偏差变化率对PID参数ΔkP,ΔkI,ΔkD进行在线自调整,使PID控制器能够适应控制的全过程[6]。模糊自适应控制系统结构如图2所示。
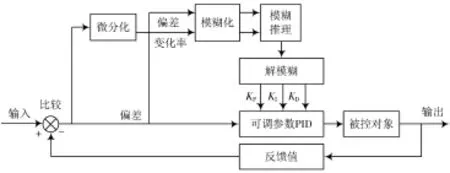
图2 模糊自适应控制系统结构图
2.2基于DOB的电液伺服控制方法
常规DOB控制系统的结构如图3所示。图中,K是一个低通的滤波器;P是控制系统的标称控制器;r是控制系统的输入信号;G是电液伺服力控制系统实际模型的传递函数;G′是电液伺服力控制系统理想模型的传递函数;d是电液伺服力控制系统受到的外界扰动信号;n是电液伺服力控制系统测量的噪声信号。通过分析常规DOB控制系统的结构,可得输出函数为[7]:
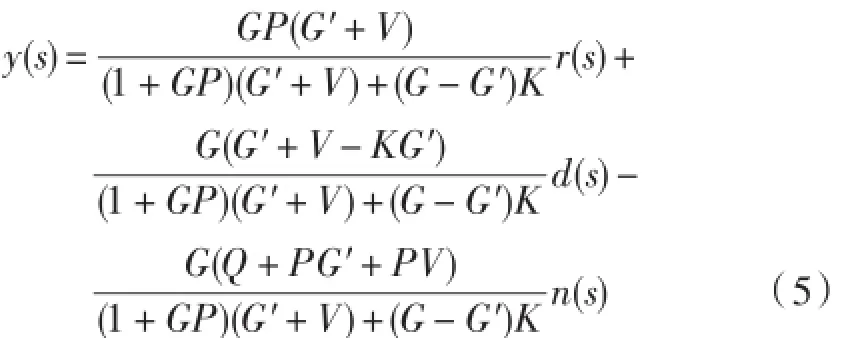

图3 常规DOB控制系统结构
通常情况下,电液伺服力控制系统受到的外界扰动信号d和电液伺服力控制系统测量的噪声信号n属于不同的频率范围,前者扰动信号为低频信号,后者测量噪声属于高频信号。故近似获得常规DOB控制系统的输出函数为:

分析式(6)可知,电液伺服力控制系统受到的外界扰动信号d被常规DOB控制系统消除,但是无法消除电液伺服力控制系统测量的噪声信号n。在此,本文对常规DOB控制系统进行改进优化,得到了改进的DOB控制系统,以消除电液伺服力控制系统测量的噪声信号n对电液伺服力控制系统的影响,其结构如图4所示。
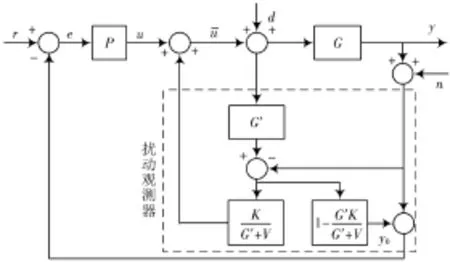
图4 改进型DOB控制系统结构
分析改进型DOB控制系统结构,可知其输出函数为:
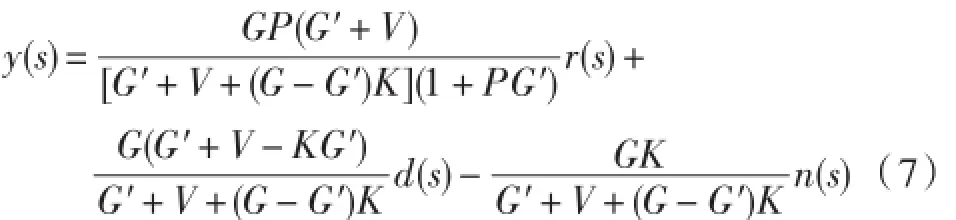
同样地,认为电液伺服力控制系统受到的外界扰动信号d和电液伺服力控制系统测量的噪声信号n属于不同的频率范围,前者扰动信号为低频信号,后者测量噪声属于高频信号。故近似获得改进型DOB控制系统的输出函数为:
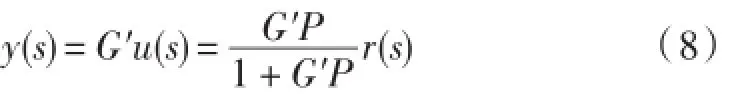
分析式(8)可知,只要对控制系统中的低通滤波器K和控制参数V进行合理的设计,即可以消除电液伺服力控制系统受到的外界扰动信号d和电液伺服力控制系统测量的噪声信号n对系统的影响。标称控制器P决定了控制系统对输入信号的跟踪能力,因此在对DOB系统进行设计时,第一步是设计标称控制器P,之后再设计低通的滤波器K和控制参数V,从而提高DOB系统的鲁棒性能。
设定电液伺服力控制系统受到的外界扰动信号d的频率是0.75 rad/s,对低通的滤波器K和控制参数V进行设计[8]:
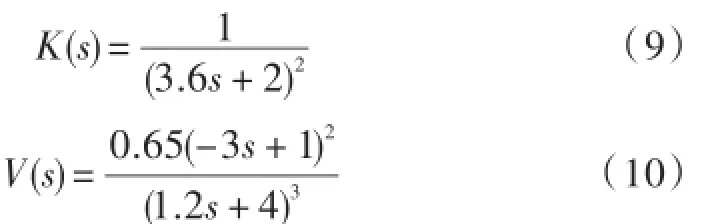
3 仿真研究
为了研究本文提出的改进型DOB系统对电液伺服力控制的性能,使用Matlab/Simulink工具箱建立电液伺服力控制系统模型。模型中的控制器分别使用基于模糊控制算法、基于常规DOB算法以及基于本文提出的改进型DOB算法进行建立。电液伺服力控制系统模型的具体参数设置如表1所示[9]。
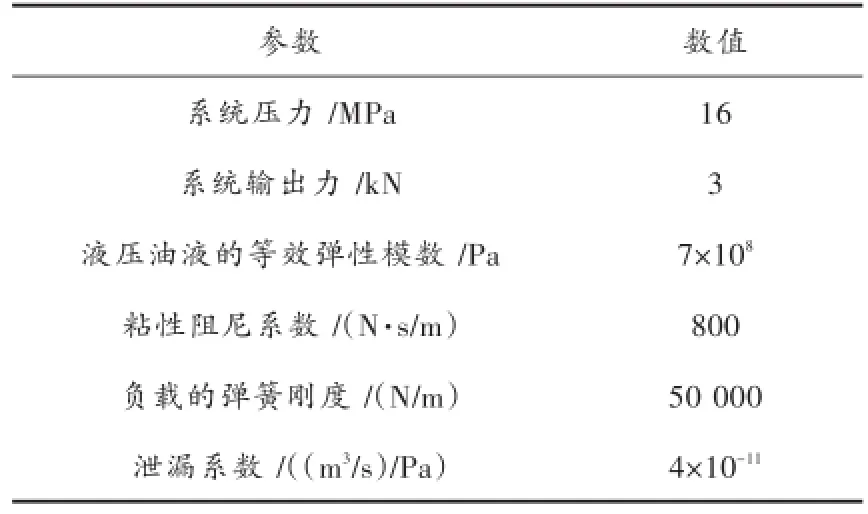
表1 电液伺服力控制系统模型的具体参数设置
设定电液伺服力控制系统受到的外界扰动信号d=2.5 sin(0.1πt)+5,则使用基于模糊控制算法、基于常规DOB算法以及基于本文提出的改进型DOB算法建立的电液伺服力控制系统的输出信号,如图5所示[10]。
根据对负载扰动作用下,电液伺服力控制系统在不同算法作用下的仿真曲线可以看出,相比DOB算法,模糊控制算法对负载扰动的抑制作用较弱,电液伺服力控制系统的输出在负载扰动作用下波动较大。基于改进型DOB算法对于负载扰动对电液伺服力控制系统影响的抑制效果比基于常规DOB算法更优,但是两种算法均能使电液伺服力控制系统的输出较好地跟踪系统输入信号,使得系统具有较好的稳定性。
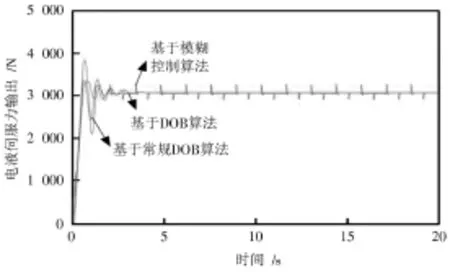
图5 负载扰动作用下不同控制算法的电液伺服力控制仿真结果
现对在电液伺服力控制系统测量的噪声信号n的影响下,使用基于模糊控制算法、基于常规DOB算法以及基于本文提出的改进型DOB算法建立的电液伺服力控制系统的响应进行研究。
设定电液伺服力控制系统测量的噪声信号n= 125 sin(50πt),则系统输出响应仿真曲线如图6所示[11]。
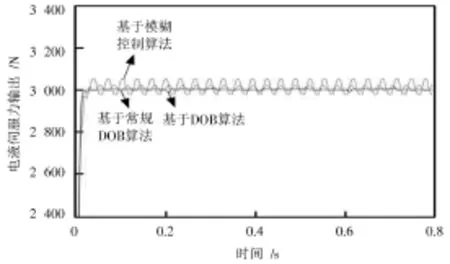
图6 测量噪声作用下不同控制算法的电液伺服力控制仿真结果
对测量噪声作用下不同控制算法的电液伺服力控制仿真结果进行研究分析可知,模糊控制算法无法对测量噪声进行有效抑制,系统会在测量噪声影响下产生较大的波动误差。基于常规的DOB算法虽然对测量噪声有一定抑制作用,但是抑制效果相比本文提出的改进型DOB算法较弱,而本文提出的改进型DOB算法能够较好地降低电液伺服力控制系统测量的噪声信号n对电液伺服力控制系统的作用,使得系统具有较好的鲁棒性和稳定性。
4 结 论
本文对电液伺服力控制系统进行了深入研究,首先建立电液伺服力控制系统的数学模型。由于电液伺服力控制系统对外界扰动影响较敏感,因此研究了一种基于改进型DOB算法的电液伺服力控制器,以消除电液伺服力控制系统受到的外界扰动信号d和电液伺服力控制系统测量的噪声信号n对系统的影响。通过仿真试验验证了本文提出的改进型DOB算法对提高电液伺服力控制系统稳定性和抗干扰能力的效果。
参考文献
[1]陈斌,史艳红,邢志伟.模糊PID控制在液压缸力控制中的应用[J].自动化技术与应用,2007,26(6):27⁃29.
[2]于少娟.电液伺服力控系统的鲁棒迭代学习控制方法研究[D].太原:太原理工大学,2012.
[3]彭昌.迭代学习滑膜控制及其在加载系统中的研究与应用[D].太原:太原科技大学,2012.
[4]李建雄.轧机电液伺服系统的鲁棒自适应输出反馈控制研究[D].秦皇岛:燕山大学,2012.
[5]汪首坤,王军政,赵江波,等.基于电液比例伺服复合加载及迭代学习控制的合成绝缘子疲劳试验方法[J].机械工程学报,2013(22):192⁃198.
[6]贾松涛,朱煜,杨开明,等.精密工作台扰动观测器的设计[J].微细加工技术,2007(4):39⁃42.
[7]谢巍,何忠亮.采用改进型扰动观测器的控制方法[J].控制理论与应用,2010,27(6):695⁃700.
[8]SHIM H,JO N H,SON Y.Disturbance observer for non⁃mini⁃mum phase linear systems[C]//Proceedings of 2008 American Control Conference.Seattle:IEEE,2008,3385⁃3389.
[9]宋君君.迭代自适应控制的研究及其在电液伺服系统上的应用[D].太原:太原科技大学,2012.
[10]郭建华.位置扰动型电液伺服力加载控制系统的研究[D].天津:中国民航大学,2008.
[11]朱勇,姜万录,刘思远,等.非线性液压弹簧力对电液伺服系统非线性动力学行为影响的研究[J].中国机械工程,2015,26 (8):1085⁃1091.
[12]廖武,钟宜生,石宗英.基于信号补偿的机械臂鲁棒控制器设计与实现[J].清华大学学报(自然科学版),2006(4):473⁃476.
中图分类号:TN876⁃34;TP27
文献标识码:A
文章编号:1004⁃373X(2016)03⁃0159⁃04
doi:10.16652/j.issn.1004⁃373x.2016.03.041
收稿日期:2015⁃08⁃12
作者简介:吕晓娟(1980—),女,回族,河南信阳人,讲师。研究方向为生产过程自动控制技术及控制仪表。
Research on electro⁃hydraulic servo force control technology based on improved DOB
LÜ Xiaojuan
(Zhengzhou Electric Power College,Zhengzhou 451450,China)
Abstract:The electro⁃hydraulic servo force control system is easily influenced by the external load disturbance,an electro⁃hydraulic servo force controller based on the improved DOB algorithm is proposed.The nominal controllerP,low pass filterK and control parameterVin the control system were designed to eliminate the influences of the noise signalnmeasured by the electric⁃hydraulic servo force control and external disturbance signald,and improve the robust performance of the DOB system. The stability and anti⁃interference ability of the electro⁃hydraulic servo force control system were verified by simulation experi⁃ments.The proposed system is compared with that of based on fuzzy algorithm and conventional DOB algorithm.The comparison results show that the improved DOB algorithm can improve the robustness and stability of the electro⁃hydraulic servo force con⁃trol system.
Keywords:electro⁃hydraulic servo;pressure control;fuzzy algorithm;disturbance observer
