基于能量耗散率的NEPE推进剂疲劳损伤分析

郭　坚,许进升,高艳宾,何　勇,陈　雄

(1.南京理工大学 机械工程学院,南京 210094;2.中国兵器工业第208研究所,北京 102202)



基于能量耗散率的NEPE推进剂疲劳损伤分析

郭坚1,许进升1,高艳宾2,何勇1,陈雄1

(1.南京理工大学 机械工程学院,南京 210094;2.中国兵器工业第208研究所,北京 102202)

摘要:为研究NEPE推进剂在应变加载条件下的疲劳损伤演化,基于循环加载过程中的推进剂耗散能变化,利用能量耗散变化比对推进剂疲劳过程进行分析。通过4个应变幅值进行了单轴拉伸疲劳试验,得到不同应变幅值下NEPE推进剂疲劳寿命,并得到在不同加载周次下的耗散能。结果表明,这种能量法能够以直观的方式解释疲劳损伤过程中损伤的累计,在对数坐标下耗散能变化比的稳定值与疲劳寿命呈明显的线性关系,稳定值随初始加载应变幅值的增大而增加。当加载应变增大时,材料稳定段相邻加载间损伤累计越快,疲劳寿命相对减小,也解释了2次循环加载间损伤发展的原理。

关键词:NEPE推进剂;耗散能;疲劳损伤;能量耗散变化比

推进剂从浇铸到服役的过程中,先后要承受温度、震动以及工作过程中的燃气压强和发射过载等诸多载荷的作用。通常温度变化及震动引起的交变载荷并不会使药柱立即发生破坏,但长期作用将在药柱内产生累积损伤,严重影响装药的结构完整性及其使用寿命。由于推进剂是一种粘弹性高聚物,对所受载荷具有记忆性,每个周期载荷所造成的损伤都需要考虑。

目前对材料疲劳特性的研究方法基本可以分为3类:唯象学法、断裂力学法和耗散能法。唯象学法采用疲劳曲线表征材料的疲劳性质,认为材料在重复载荷作用下引起强度衰减[1],进而直接测定疲劳周期与设计指标之间的回归关系。目前使用最广泛的是Miner线性损伤累计法则,通过实验获得应力-寿命曲线[2-3]。NEPE推进剂属于粘弹性材料,文献[4～5]认为粘弹性材料的疲劳损伤演化过程更符合非线性损伤,即损伤与加载过程相关,载荷处于损伤的不同阶段产生的损伤效果不同。断裂力学法通过跟踪观察疲劳过程中裂纹发展状况研究疲劳,它的原理是检测裂纹的张开尺寸并计算裂纹顶端的应力强度因子[6],Paris公式建立了应力强度因子与裂纹扩展速率之间的关系。这种方法的局限性在于实验设备复杂,另外应力强度因子在高温下不是常数。耗散能法是近年来研究累计损伤的最新方法,在沥青、岩石及复合材料等领域中得到了广泛应用,在固体推进剂方面,国内也有相关研究[7-8],并取得了一定的成果,但是研究的重点集中在疲劳破坏累积耗散能与加载周次间的关系,然而在运用耗散能理论对疲劳损伤的机理分析上,目前的研究还不够深入[9]。

固体推进剂疲劳损伤的累积过程本质上是一种能量非均匀耗散的不可逆过程,NEPE推进剂是一种多组分高固含量的复合材料[10],为使材料破坏必须提供一定的能量来克服内部固体颗粒和基体之间的结合能[11]。本文以应变控制疲劳实验为基础,基于耗散能原理提出耗散能变化比的概念,通过分析加载周次中耗散能的变化,进一步阐述疲劳中损伤的积累过程。

1耗散能基本原理

1.1迟滞回线与耗散能

对材料施加应力σ载荷时可产生应变ε响应,输入材料内部的能量可通过应力-应变曲线所形成的图形面积表示。当应力卸载后应变可逐渐恢复,若加载与卸载应力-应变曲线一致,说明所有输入材料的能量都能恢复,若加载与卸载曲线不一致,则说明材料在该载荷周次内存在一定的能量损耗。图1为NEPE推进剂恒应变控制的疲劳试验结果,在不同周次(N)迟滞回线的形状也不同,即在循环加载的不同阶段材料耗散的能量不等。疲劳实验的初始阶段滞后环面积较大,耗散能较多,随着重复荷载作用次数的增加,耗散能逐渐变小。

图1　恒应变疲劳实验应力-应变迟滞曲线

以正弦波加载模式为例,每个应力周次消耗的能量为该周次滞后回线的面积,第i个加载周次的耗散能计算公式为

(1)

式中:Wi为在第i次加载周次中的耗散能,角频率ω=2πf,f为加载频率。

Khalid[12]指出,在整个疲劳寿命过程中累积耗散能是所有滞后回路面积的总和,累积耗散能表示为

(2)

式中:WNf为疲劳失效时总的耗散能。

文献[13]中首次将耗散能与疲劳寿命统一起来,关系如下:

(3)

式中:Nf为疲劳寿命,A和Z为材料常数。

1.2耗散能变化比

疲劳累积耗散能与疲劳寿命存在一定的关系是基于这样的一个假设:所有耗散的能量都用于材料的损伤。实际上,这是不正确的,对于NEPE这种粘弹性材料,加载与卸载路径的非弹性响应有两方面的特征:材料粘弹性本质(外力的功因材料的粘性流动而被消耗)和损伤累计(外力的功使裂纹产生、扩展)。因流动而被消耗的能量指材料受到外部载荷作用时其内部组织结构发生重组变化来抵抗外部载荷作用而消耗的能量。这部分能量转化为热能被释放或部分保存在试件中,进而使试件温度升高。在外载的作用下,损伤通过裂纹尺寸的改变而表现出来,由于该阶段材料的损伤无法显示和直接测量,只能通过部分可测参量或间接可测参量的变化来间接度量损伤程度。根据损伤力学理论,随加载周次而变化的耗散能可以作为一种评估损伤的量。

材料内部损耗是疲劳破坏的主要原因,Ghuzlan[14]认为2次相邻载荷过程中变化的耗散能是材料损伤的原因,并定义了能量耗散率η,表达式为

(4)

式中:Wi+1为第i+1次加载周次的耗散能密度,Wi为在第i次加载周次的耗散能。

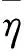
(5)

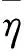
为使在整个温度范围与加荷时间内对粘弹性材料力学性质有一个统一、简便、实用的综合评价体系,引入刚度模量的概念,其定义为循环加载过程中应力峰值与应变峰值的比值。按照传统的应变加载疲劳失效定义方法,定义当刚度模量降低至初始模量的50%时,材料失效,此时的加载周次即为寿命值Nf,并认为从该载荷周次起材料的耗散能变化比达到稳定值Vs而不再变化[15],Vs代表在疲劳失效点材料吸收的耗散能用于损伤部分的比重。

2试验及结果分析

2.1试验方法

本文所研究的NEPE推进剂基本组成有PEG粘合剂、AP和HMX氧化剂、燃料铝粉、NG/BTTN增塑剂,其中固体含量达到70%～73%。为保证实验数据的准确与可靠性,选用同一批次的某NEPE浇铸推进剂坯料。疲劳测试在美国BOSE公司的DMA(动态热机械分析仪)平台上进行。本文参照文献[16]中的单轴拉伸实验方法设计了疲劳试验试样与夹具。试件与拉头之间用环氧树脂胶粘结,试件的有效尺寸为长(15±1.5)mm、宽(5.5±0.5)mm、厚(5.5±0.5)mm。试件及其在试验机中的装夹情况如图2所示。

本文采用单轴拉伸应变控制式疲劳试验方法进行试验。试验温度为常温,加载频率为10 Hz,加载波形为半正矢疲劳应变,应变幅值定义为

Δε=εmax-εmin

式中:εmin=0,分别取Δε为0.2,0.3,0.4,0.5进行试验。每个实验条件重复多次并保证5个有效试件。由于在应变控制条件下试件不会出现明显的断裂破坏,应力衰减到一定的水平后呈稳定状态,以刚度模量衰变至初始模量的50%作为疲劳判据,此时的循环周次为疲劳寿命Nf。

图2　试件结构及装夹示意图

2.2NEPE推进剂疲劳损伤微观分析

为研究有损伤造成的疲劳软化机理,对Δε=0.4的疲劳试件在循环过程中的微观组织变化进行显微观察。图3为往复拉伸N次后,将试件再次拉伸至Δε时的微观内部结构图。图3(a)为未拉伸时NEPE推进剂表面的细观形貌,发亮点为AP(高氯酸铵)颗粒,特点是表面光滑,含量高,分布不均匀,大颗粒多呈圆形和椭圆形。图3(b)为第一次拉伸至Δε时的微观图,当应变达到峰值点时,许多形状不同的颗粒与基体沿界面出现撕裂,也称为脱湿点。脱湿点首先出现在大颗粒及大颗粒聚集区,说明大颗粒与基体的结合部分更容易发生脱湿。在进行循环加载时,脱湿点经过闭合张开的过程,在循环初期孔洞迅速扩大,如图3(c)～图3(d),造成推进剂刚度下降迅速,这是材料出现软化的原因。当脱湿点在基体上基本达到饱和时,孔洞的变化逐渐稳定,如图3(e)～图3(h)所示。

NEPE推进剂属于颗粒增强型复合材料,图3中所观察到的颗粒主要为AP(高氯酸铵),从中可以观察到,原始材料在加工生产过程中会存在一些缺陷,如基体裂纹,基体与颗粒结合界面不均匀。在疲劳开始的初期,脱湿首先沿着颗粒与基体之间的粘接界面发展,伴随着加载过程,基体存在的小裂纹形核也快速扩展为大裂纹,造成材料的刚度迅速下降。当材料内部原先存在的粘接界面不均匀以及基体小裂纹逐渐消耗完毕,产生新脱湿界面和基体裂纹形核的进展变得缓慢,进入性能稳定区。

图3　往复拉伸过程中推进剂脱湿形貌示意图

2.3粘弹性力学表征

考察NEPE推进剂粘弹特性是通过考察材料对外界刺激的响应程度来分析的,NEPE推进剂的松弛与蠕变参量都是在准静态的条件下确定,但在交变载荷下,刚度模量Es是研究材料粘弹性的重要参量。以应变幅值为0.2的疲劳加载为例,分析NEPE推进剂粘弹性与损伤特性。从图4刚度模量演化曲线可知,在应变控制下的疲劳试验中,刚度模量随着载荷周次的增加呈逐渐减小的趋势,呈现出明显的2个阶段。第一阶段推测是由于热量的耗散以及损伤的萌生,刚度模量迅速下降,损伤增长速度较快,时间较短;接着进入第二阶段为损伤稳定增长阶段。

耗散能W可通过计算相应的迟滞回线面积获得。由图5可知,耗散能在加载初期有明显下降,这可能是因为在加载初期阶段推进剂中产生了大量的畸变组织,大量能量储存于这些组织当中。随着加载周次的增加,变化逐渐平缓,进人循环稳定阶段,显微结构也趋于稳定变化。

图4　刚度模量随载荷周次增加的变化

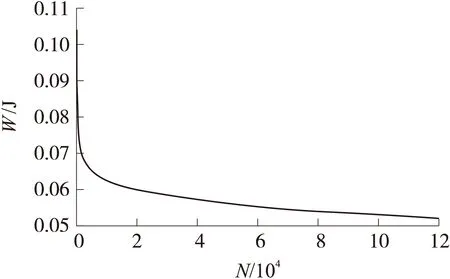
图5　耗散能随载荷周次增加的变化

2.4能量耗散变化比

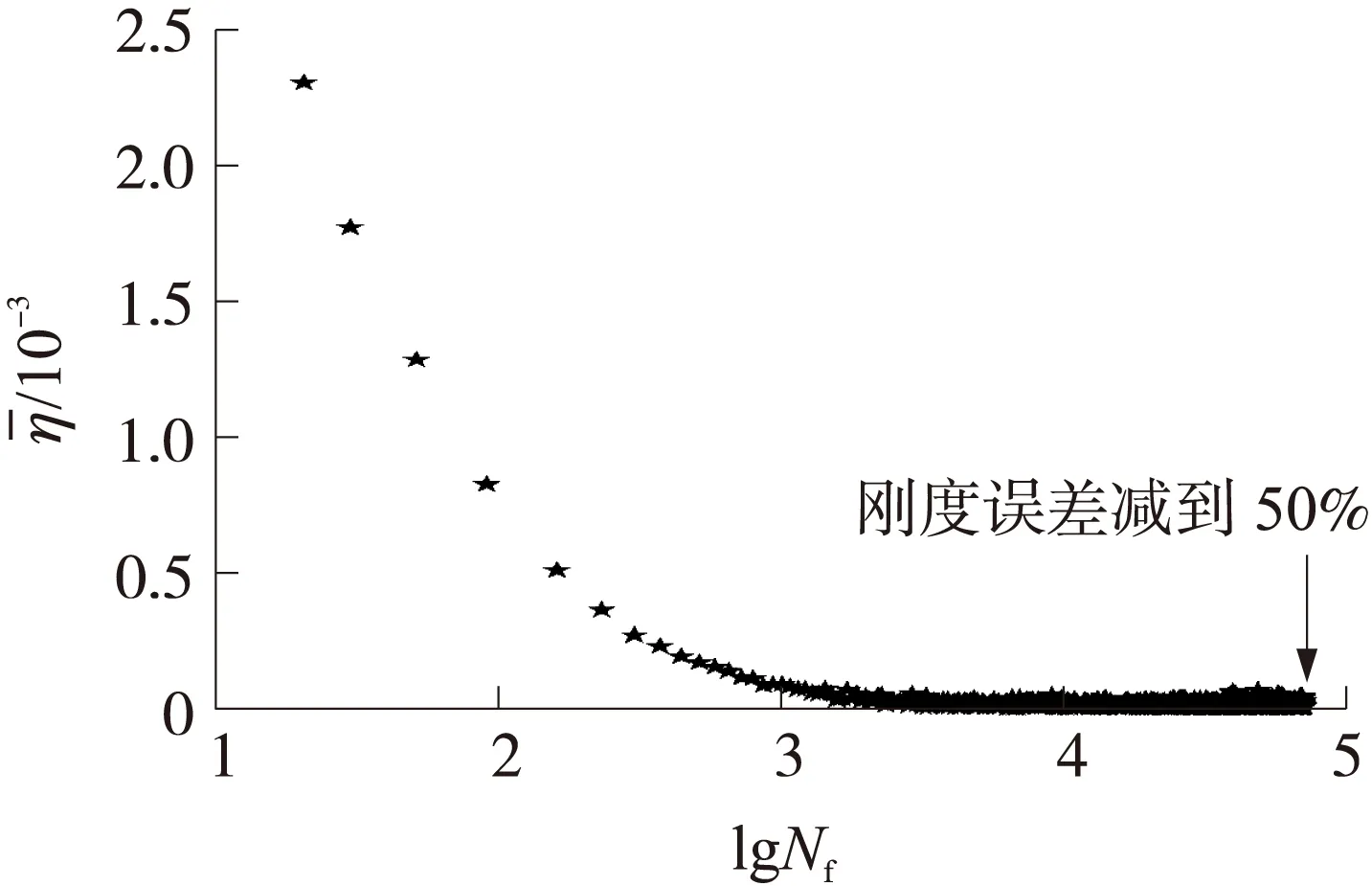
图6　耗散能变化比与加载周次的变化关系

随着疲劳过程的深入,推进剂耗散能变化比先迅速减小然后趋于稳定。在定应变幅值的往复拉伸过程中,耗散能变化比的规律由推进剂内部损伤的发展决定。由于NEPE是颗粒复合推进剂,初期加载阶段,由于外载荷作用,推进剂内部应力-应变分布很不均匀,颗粒与基体之间出现脱湿,基体分子链中大量短链断裂,这都需要吸收大量的能量。根据细观结构变化特征可知,随着加载周次的增加,材料内部组织结构变化趋于稳定,颗粒与基体之间的脱湿以及基体分子链断裂减少,材料损伤发展速度变缓,吸收的能量减小,材料在疲劳载荷下吸收的能量所造成损伤的比例也逐渐降低。

对应变幅度Δε为0.3,0.4,0.5的疲劳实验采用相同的数据处理方法,获得不同应变幅度下NEPE推进剂的疲劳寿命和耗散能变化比稳定值。不同应变幅值疲劳实验的稳定值Vs与疲劳寿命Nf的对数关系如图7所示。

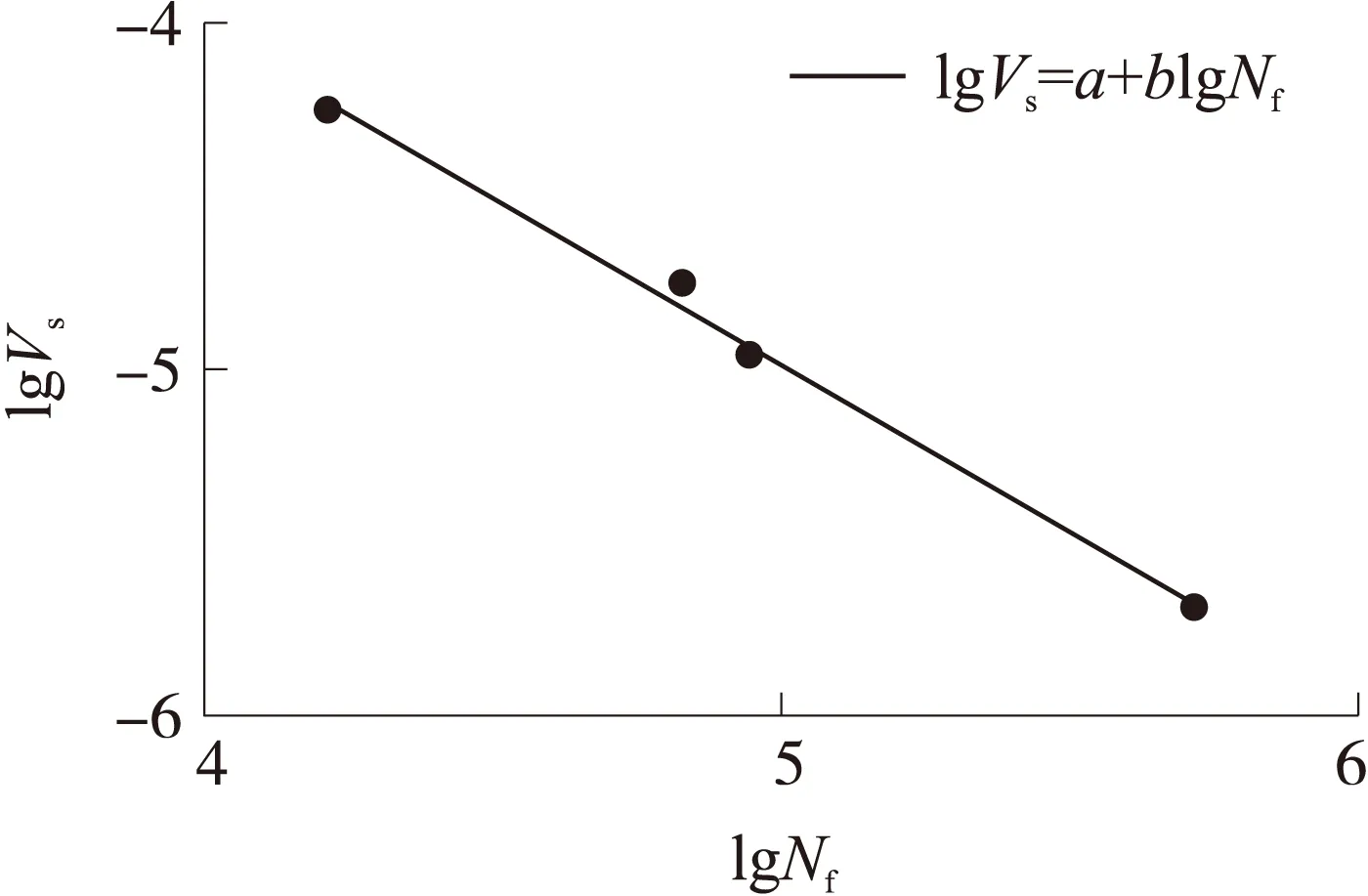
图7　不同应变幅值的稳定值与疲劳寿命的对应关系

(6)

由图7可见,在对数坐标系下,稳定值Vs与疲劳寿命Nf呈现出明显的线性关系,并随着疲劳寿命Nf的增加而逐渐减小。

应变幅值与疲劳寿命曲线如图8所示,应变幅值Δε越大,即外界条件越恶劣,材料抵抗外部加载导致自身性能的退化,疲劳寿命Nf就越小。

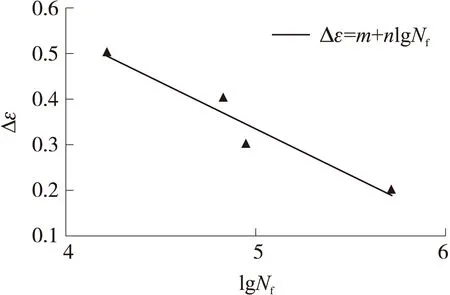
图8　应变幅值与疲劳寿命对应关系

(7)

如果稳定值Vs能够表征材料稳定损伤段能量耗散新特征,则应变幅值Δε与稳定值间就存在一定的关系,通过疲劳寿命Nf将稳定值Vs与应变幅值Δε联系起来,即由式(6)和式(7)可得:

lgVs=-6.58+4.75Δε

(8)

为验证上述关系,图9给出稳定值Vs随加载幅值Δε的变化关系,拟合得到:

lgVs=-6.50+4.52Δε

(9)

比较式(8)和式(9)可得,公式中的参数差距很小,这表明耗散能变化比的稳定值Vs能够作为分析材料疲劳损伤的依据。当加载应变增大时,材料稳定段相邻加载间损伤累计越快,疲劳寿命相对减小,同时也解释两次循环加载间损伤发展的原理。

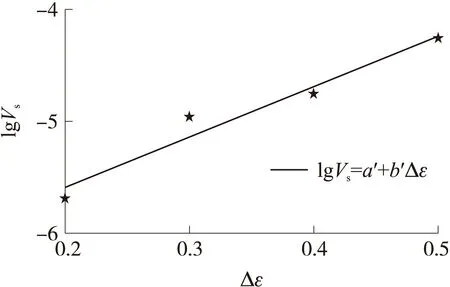
图9　稳定值Vs随加载幅值Δε的变化关系

3结束语

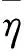
②能量耗散变化比解释了相邻加载周次中损伤的增长程度,在应变控制疲劳实验条件下,随着循环周次增加,耗散能减小,用于造成NEPE推进剂疲劳损伤那一部分的能量也随之减小,使得能量耗散变化比也减小。

③稳定值Vs与疲劳寿命Nf在对数坐标系下呈明显的线性关系,疲劳寿命越高,稳定值越小;稳定值依赖于初始加载条件,疲劳应变幅值越大,稳定值越大。

参考文献

[1]BAZIN P,SAUNIER J.Deformability,fatigue and healing properties of asphalt mixes[C]//Intl Conf Struct Design Asphalt Pvmts.Ann Arbor:MI,1967:553-569.

[2]曲凯,张杰,张旭东.舰船运动对固体火箭发动机粘接界面疲劳损伤研究[J].兵工学报,2012,33(8):986-990.

QU Kai,ZHANG Jie,ZHANG Xu-dong.Research on effects of ship motion on interface fatigue damage of solid rocket motor[J].Acta Armamentarii,2012,33(8):986-990.(in Chinese)

[3]曲凯,邢耀国,张旭东.摇摆载荷作用下舰载固体火箭发动机药柱疲劳损伤[J].航空动力学报,2011,26(11):2 636-2 640.

QU Kai,XING Yao-guo,ZHANG Xu-dong.Fatigue damage of shipborne solid rocket motor propellant under swing loading[J].Journal of Aerospace Power,2011,26(11):2 636-2 640.(in Chinese)

[4]CASTRO M,SáNCHEZ J A.Estimation of asphalt concrete fatigue curves-a damage theory approach[J].Construction and Building Materials,2008,22(6):1 232-1 238.

[5]LEE H J,KIM Y R.Viscoelastic constitutive model for asphalt concrete under cyclic loading[J].Journal of Engineering Mechanics,1998,124(1):32-40.

[6]MAJIDZADEH K,KAUFFMANN E M,RAMSAMOOJ D V.Application of fracture mechanics in the analysis of pavement fatigue[C]//Association of Asphalt Paving Technologists Proc.St Paul:TRB,1971:227-246.

[7]邢耀国,曲凯,许俊松,等.舰船摇摆条件下固体火箭发动机舰载寿命预估[J].推进技术,2011,32(1):32-35.

XING Yao-guo,QU Kai,XU Jun-song,et al.Life prediction of shipborne solid rocket motor under the ship swing motion[J].Journal of Propulsion Technology,2011,32(1):32-35.(in Chinese)

[8]刘逸平,何庭蕙,黄小清.基于耗散能原理的冲击损伤与疲劳损伤耦合分析[J].兵工学报,2010(S1):223-226.

LIU Yi-ping,HE Ting-hui,HUANG Xiao-qing,et al.Coupling analysis on impact damage and fatigue damage based on dissipated energy theories[J].Acta Armamentarii,2010(S1):223-226.(in Chinese)

[9]CARPENTER S H,JANSEN M.Fatigue behavior under new aircraft loading conditions[C]//Aircraft/Pavement Technology in the Midst of Change.New York:ASCE,1997:259-271.

[10]胡少青,鞠玉涛,常武军.NEPE 固体推进剂粘-超弹性本构模型研究[J].兵工学报,2013,34(2):168-173.

HU Shao-qing,JU Yu-tao,CHANG Wu-jin,et al.A visco-hyperelastic constitutive behaviour of NEPE propellant[J].Acta Armamentarii,2013,34(2):168-173.(in Chinese)

[11]邓斌,董可海,谢燕.基于能量耗散的药柱粘弹性累积损伤[J].国防科技大学学报,2013,35(1):24-27.

DENG Bin,DONG Ke-hai,XIE Yan.Viscoelastic cumulative damage of dolid propellant grain based on energy dissipation[J].Journal of National University of Defense Technology,2013,35(1):24-27.(in Chinese)

[12]GHUZLAN K A,CARPENTER S H.Fatigue damage analysis in asphalt concrete mixtures using the dissipated energy approach[J].Canadian Journal of Civil Engineering,2006,33(7):890-901.

[13]Van DIJK W,MOREAUD H,QUEDEVILLE A,et al.The fatigue of bitumen and bituminous mixes[C]//Presented the Third International Conference on the Structural Design of Asphalt Pavements.London:TRB,1972:254-366.

[14]GHUZLAN K A,CARPENTER S H.Energy-derived,damage-based failure criterion for fatigue testing[J].Transportation Research Record:Journal of the Transportation Research Board,2000,1 723(1):141-149.

[15]AL-KHATEEB G,SHENOY A.A distinctive fatigue failure criterion[J].Journal of the Association of Asphalt Paving Technologists,2004,73:585-622.

[16]JUNG G D,YOUN S K.A nonlinear viscoelastic constitutive model of solid propellant[J].International Journal of Solids and Structures,1999,36(25):3 755-3 777.

Fatigue Damage Evaluation of NEPE Propellant Based on Dissipated Energy

GUO Jian1,XU Jin-sheng1,GAO Yan-bin2,HE Yong1,CHEN Xiong1

(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China;2.No.208 Research Institute of China Ordnance Industries,Beijing 102202,China)

Abstract:To study the fatigue damage evolution of NEPE propellant in controlled strain fatigue tests,the ratio of dissipated energy change-approach based on the distribution of dissipated energy was used to analyze the fatigue damage process.According to four strain-amplitudes,the uniaxial drawing fatigue test was conducted.The fatigue life and dissipated energy under different strain-amplitudes were obtained.The result shows that the energy approach can intuitively explain the damage accumulation in the process of fatigue damage.Plotting plateau value of ratio of dissipated-energy and fatigue life behave in a linear relation.The plateau value is highly dependent on the initial loading strain amplitude,and the plateau value increases with the strain amplitude.The accumulative rates of the damage increase with the strain levels for the adjacent loading cycles,but the fatigue life decreases relatively,and the mechanism of damage increasing between the adjacent loading cycles can be explained.

Key words:NEPE propellant;dissipated energy;fatigue damage;ratio of dissipated energy change

收稿日期:2015-12-30

基金项目:江苏省青年基金项目(BK20140772);中央高校基本科研业务费专项资金资助(30915011301;30915118805)

作者简介:郭坚(1978- ),男,博士研究生,研究方向为终点效应。E-mail:13725292@qq.com。 通讯作者:许进升(1985- ),男,讲师,博士,研究方向为固体火箭发动机装药结构完整性分析。E-mail:xujinsheng@njust.edu.cn。

中图分类号:V311

文献标识码:A

文章编号:1004-499X(2016)02-0062-06