基于RBF神经网络的中密度纤维板连续热压板厚动态面控制1)

朱良宽　王子博　刘亚秋

(东北林业大学，哈尔滨，150040)



基于RBF神经网络的中密度纤维板连续热压板厚动态面控制1)

朱良宽王子博刘亚秋

(东北林业大学，哈尔滨，150040)

摘要针对中密度纤维板(MDF)连续热压工艺特点，考虑到定厚段外负载力干扰对板坯厚度产生的影响，提出一种基于径向基函数(RBF)神经网络的动态面板厚度跟踪控制策略。将连续热压机的电液位置伺服系统作为被控对象，首先利用RBF神经网络逼近其外负载力干扰，设计自适应律对网络权值进行调整；然后采用动态面控制(DSC)方法，通过引入一阶低通滤波器计算虚拟控制量导数，避免了反步法设计控制器时易出现的微分项膨胀问题；最后通过选择合适的Lyapunov函数，证明了闭环系统所有信号半全局一致最终有界，且跟踪误差最终渐进收敛为零。仿真结果表明，所提方法可以有效地确保MDF板厚度跟踪控制精度，并使系统具有较强的鲁棒性。

关键词中密度纤维板；连续热压；板厚控制；径向基函数神经网络；动态面控制

中密度纤维板(MDF)因具有均匀的密度、平整的表面和良好的力学性能等诸多优势，使得其在人造板生产中的比重不断扩大[1]。连续热压机作为目前生产人造板的关键设备，其生产能力和技术性能直接制约着企业的生产规模及产品质量，并一度成为人造板企业具备先进性的标志[2]。

热压是MDF生产中一道重要工序，主要通过加热和加压将预压过后的板坯固化成型，并送至最后一道工序制成一定规格的成品[3]235。然而，在其工艺的定厚段，由于板坯内部存在蒸气压力，容易使得其厚度精度产生偏差，进而影响板坯的固化成型，最终造成MDF成品的质量和产量下降。因此，定厚段的板坯厚度跟踪控制问题十分值得研究。

目前，连续热压机主要采用电液位置伺服系统，通过液压缸活塞带动热压板运动将板坯压制到规定厚度[4]。针对其板坯厚度跟踪控制的研究成果还很有限，刘亚秋等设计了基于零相差前馈跟踪的PID控制器，虽然可以实现无超调、无偏差地跟踪控制，但是没有给出严格的稳定性证明[5]。考虑到电液位置伺服系统通常为三阶或三阶以上的积分串级系统，反步法在设计控制器时得到了学者们广泛的采用[6-9]。其中,邵小东等没有考虑外负载力变化对控制系统的影响[6]，因而其控制方法不具备鲁棒性；相关学者们又进一步结合自适应理论、观测器理论和滑模变结构理论有效地避免了外界干扰对系统的影响[7-9]。但由于反步法中需对虚拟控制量和参考输入信号反复求导，使得系统中微分项膨胀，进而增加了控制器的复杂度，产生工程上所谓的“复杂度爆炸”问题。

为解决控制器中出现的“复杂度爆炸”问题，Swaroop等学者于1997年首次提出了动态面控制(DSC)[10]，其思想核心是在传统反步法的基础上，通过引入n-1个一阶低通滤波器(n为系统阶数)去计算每步中虚拟控制量的导数，进而消除了系统中微分项的过度膨胀，极大地简化了控制器的设计。因而被广泛地用于汽车的自动行驶控制[11]、导弹的制导控制[12]乃至航天器的姿态控制[13]等诸多领域。但是考虑到应用常规的DSC方法设计控制器难以使系统具备较强的鲁棒性，王丹教授等针对一类严格反馈控制系统提出了基于RBF神经网络的DSC控制策略，利用RBF神经网络的基函数的逼近特性，逼近系统中不确定的非线性函数，并通过自适应律对神经网络权值进行调整[14]。

笔者借鉴上述思想，提出一种基于RBF神经网络的动态面厚度跟踪控制方法。首先利用RBF神经网络逼近系统中外负载力干扰并对控制律进行补偿，给出了神经网络权值的自适应律；然后设计了动态面控制器，引入一阶低通滤波器计算虚拟控制量的导数。最后，通过仿真实验来验证所提出的控制策略的可行性和有效性。

1热压工艺及系统描述

1.1热压工艺

热压顾名思义是指，对预压过后的MDF板坯加热加压，加热起到使纤维化学组分充分降解，激发其活性，并在纤维间产生结合力的作用；加压的目的是克服纤维的反弹力，排出纤维中的水蒸汽，使纤维之间充分交织，并将板坯压到规定厚度[3]236。其工艺过程在压机长度分布上，大致可分为3段，如图1所示[15]。

从生产角度来看，直接决定MDF板材品质优劣的阶段为定厚段(即图1中两条曲线的汇合段)，它对MDF板坯固化成型尤为关键。在此阶段温度和压力在合理的范围内，主要是排出板坯中剩余的水蒸汽，以避免出现鼓泡、分层等缺陷，并且使其获得稳定的厚度。然而在定厚段，由于MDF板坯内部蒸气压力的存在，使得其易出现厚度偏差，从而相对较厚的区域在压力不变的情况下，水蒸汽排出不充分，造成了MDF板材品质下降。由此看出，在此阶段应对板坯进行严格的厚度控制。

a段为热压板快速闭合段；b段为加温加压段；c段为泄压和定厚段。

图1MDF厚度在热压机长度分布上的变化

1.2连续热压机控制系统

连续热压机的控制系统目前主要采用电液位置伺服系统，其系统原理图如图2所示[6]。系统在定厚段的工作过程为通过位移传感器采集回来的液压缸活塞位置信号(y)与给定位置信号(yd)进行比较形成偏差信号输入控制器；控制器输出电压(u)通过伺服放大器形成电流信号送给伺服阀，伺服阀按照固定比例将电流信号转变成阀芯的运动，向液压缸提供油量，最终液压缸活塞带动热压板运动将板坯压制到规定厚度。从工作过程来看，控制器设计目标在于使系统快速并且准确地跟踪给定的位置信号，以确保MDF板坯的厚度不出现偏差。

图2　MDF连续热压机的电液位置伺服系统原理图

1.3数学模型建立

将单个液压缸作为研究对象，液压缸选用的是四通阀控对称液压缸，四通阀控液压缸动力机构的3个基本方程如式(1)，详细推导和参数定义见参看文献[16]。

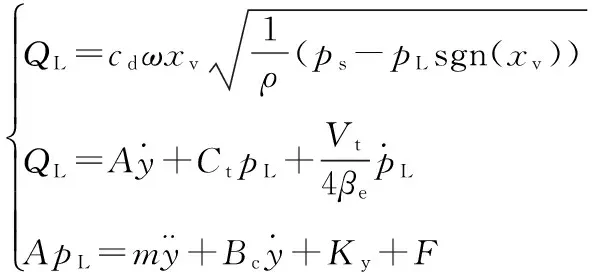
(1)

伺服放大器可以等效为比例环节，而伺服阀输入电流与阀芯位移之间的关系也可以等效为比例环节，有式(2)成立：

Ksv=xv/i,Ka=i/u。

(2)

式中：Ksv为伺服阀增益；Ka为伺服放大器增益；i为伺服阀输入电流；u为控制器输出电压。

(3)

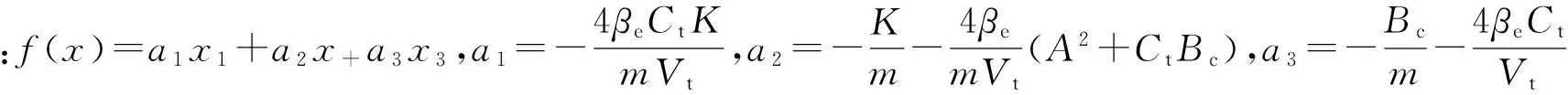
由于定厚段板坯内部存在蒸气压力，所以外负载力(F)随时间不断变化，进而对系统形成的干扰(d)为不确定的，致使系统模型建立不精确。

2基于RBF神经网络的动态面控制器设计

基于RBF神经网络的动态面控制系统如图3所示。首先利用RBF神经网络逼近MDF连续热压机电液位置伺服系统的不确定性并将其用于补偿，然后针对补偿后的模型设计动态面控制律。考虑到神经网络的权值选取问题，所以设计了权值的自适应律。

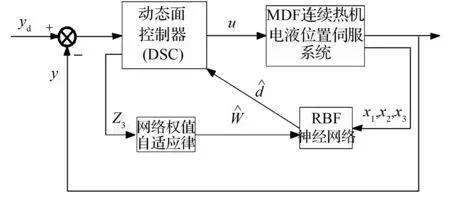
图3　基于RBF神经网络的动态面控制系统

2.1动态面控制器的设计

针对系统(3)，动态面控制器设计步骤如下：

定义第一个子系统的跟踪误差为

z1=y-yd=x1-yd；

(4)

根据反步法的思想，设计虚拟控制量

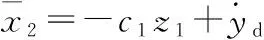
(5)

式中：正整数c1为待设计参数。

(6)

定义第二个子系统的跟踪误差为

z2=x2-x2d;

(7)

设计虚拟控制量

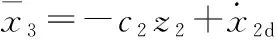
(8)

式中：正整数c2为待设计参数。

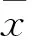
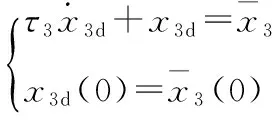
(9)

定义第三个子系统的跟踪误差为

z3=x3-x3d;

(10)

设计如下控制律

(11)

式中：正整数c3为待设计参数。

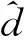
2.2RBF神经网络逼近系统不确定项

RBF神经网络的结构如4图所示，X=[xi]T为系统输入，H=[hj]T为径向基函数，通常选择高斯函数作为激活函数[17]201，[18]：

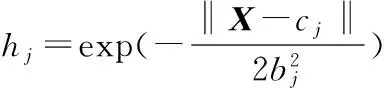
(12)

式中：cj为高斯函数的中心坐标；bj为对应神经元高斯函数的宽度。其网络权值为WT，网络输出。

ym=WTH。

(13)

图4　RBF神经网络结构

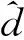
d=W*TH;

(14)

(15)

通过式(14)、(15)得，

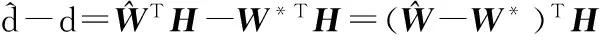
(16)

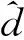
所以控制律(11)改为

(17)

针对RBF神经网络权值的选择，梯度下降法是一种常用的方法，但是其易陷入局部最优，并且对于系统稳定性无法给出较为严格的证明。本研究借鉴文献[14]的思想，基于Lyapunov函数设计了在线自适应律来调整网络权值，

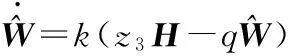
(18)

式中：正实数k和q为待设计参数。

3稳定性分析

针对系统(3)，采用DSC方法设计步骤虽然很简洁，但是由于一阶低通滤波器、RBF神经网络和自适应律的引入，使得稳定性分析略具复杂性。在选择Lyapunov函数时需要综合考虑3个子系统的跟踪信号误差、一阶低通滤波器计算虚拟控制量时产生的误差及RBF神经网络权值估计误差，为分析方便做出如下定义[10]：

定义滤波误差y2和y3，

(19)

对y2求导可得

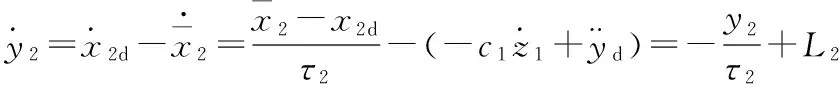
(20)

式中：

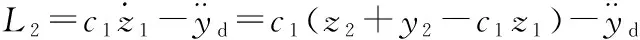
(21)

通过式(21)可以看出，L2是有界的。

同理可得，

(22)

式中：L3是有界的。

定义集合[19]

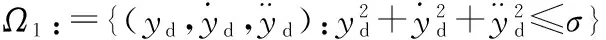
式中：Ω1∈R3,Ω2∈R6;所以Ω1×Ω2∈R9。

定理：针对系统(3)，在控制律(17)作用下，采用RBF神经网络逼近得到的(15)，选取适当的动态面增益常数ci(i=1、2、3)和一阶低通滤波器时间常数τi(i=2、3)，并且根据自适应律(18)调整网络权值，可以保证闭环系统半全局一致最终有界，且跟踪误差渐进收敛为零。

证明：构造Lyapunov函数如下

(23)

对V求导并代入式(14)可得，

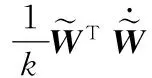
(24)

将式(5)、(8)以及(17)代入式(24)，得

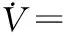
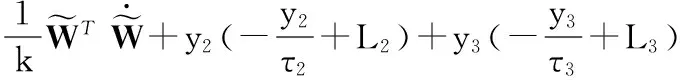
(25)

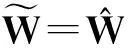
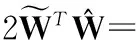
(26)

将式(18)和式(26)代入式(25)，整理可得

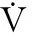
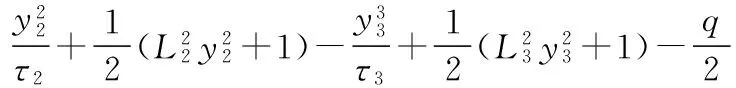
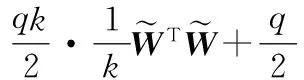
(27)

取参数

(28)

式中：r为正实数；则有

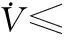
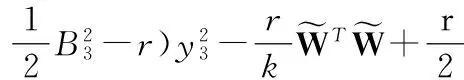
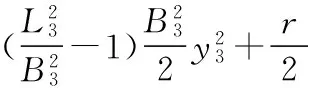
(29)

代入参数整理得

(30)

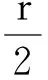
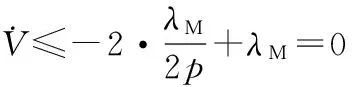
(31)

进一步由式(30)、(31)可得

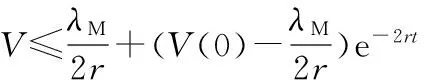
(32)

由式(32)知，闭环系统所有信号在集合Θ上半全局最终一致有界。

Θ={z1,z2,z3,y2,y3}。

通过调整动态面增益常数ci(i=1、2、3)和一阶低通滤波器时间常数τi=(i=2、3)，集合Θ可以变得任意小，所以跟踪误差z1最终渐进收敛为零。

4仿真分析

针对MDF连续热压机的电液位置伺服系统，考虑热压工艺的定厚段，为验证本研究提出控制策略的有效性，应用Matlab2014a/Simulink进行仿真实验。保证其它条件在合理范围内的前提下，系统的主要标称参数如下：

Ksv=0.01 m·A-1,Ka=0.012 5A·V-1,

cd=0.61，ρ=850 kg·m-3,A=0.125 6 m2,

Bc=2.25×106N·s·m-1,K=2.4GN·m-1,

ps=25 MPa,Ct=5×10-16m5·N-1·s-1,

ω=0.025 m,βe=685 MPa,F=54 780 N,

Vt=2.356×10-3m3,m=Mg,pL=16.67 MPa。

假设液压缸活塞的初始位置为x0=0，为消除板坯厚度偏差，需要对板坯进行微调0.1 mm，所以给定的期望位置信号为yd=0.1 mm，对其进行位置跟踪。

本研究选取的仿真参数如下：①动态面控制器的参数。动态面增益常数为c1=c2=c3=80，一阶低通滤波器时间常数为τ2=τ3=0.001；②RBF神经网络参数。高斯函数中心为ci=0.000 1×[-4 -3 -2 -1 0 1 2 3 4]，i=1、2、3，高斯函数的宽度bi=1,i=1、2、3，网络结构为3-9-1。网络权值的自适应系数γ=2×105。假设外负载力为F=54 780+4 000sin(4πt)。

注3：Bongsob指出，增大动态面增益，并减小一阶低通滤波器时间可以改善控制系统动态性能[20]。但是不能使动态面增益过大，一阶低通滤波器时间常数过小，因为会造成控制器输出电压过高，超出电液位置伺服系统执行机构所能承受的电压范围，使系统失稳而不能处于正常工作状态。

注4：RBF神经网络参数的选择方面，高斯函数中心的选取要根据网络输入的实际范围进行选取[17]189，因而需要在隐含层神经元高斯函数中心位置向量前加一个系数。

仿真结果如图5—图10所示。图5展示了不引入RBF神经网络逼近外负载力干扰的情况下，位置跟踪曲线和跟踪误差情况，无法精准跟踪位置信号。由于热压工艺过程不可逆，位置跟踪的超调现象是绝对不能允许的，足以见得本研究提出的控制策略的必要性。

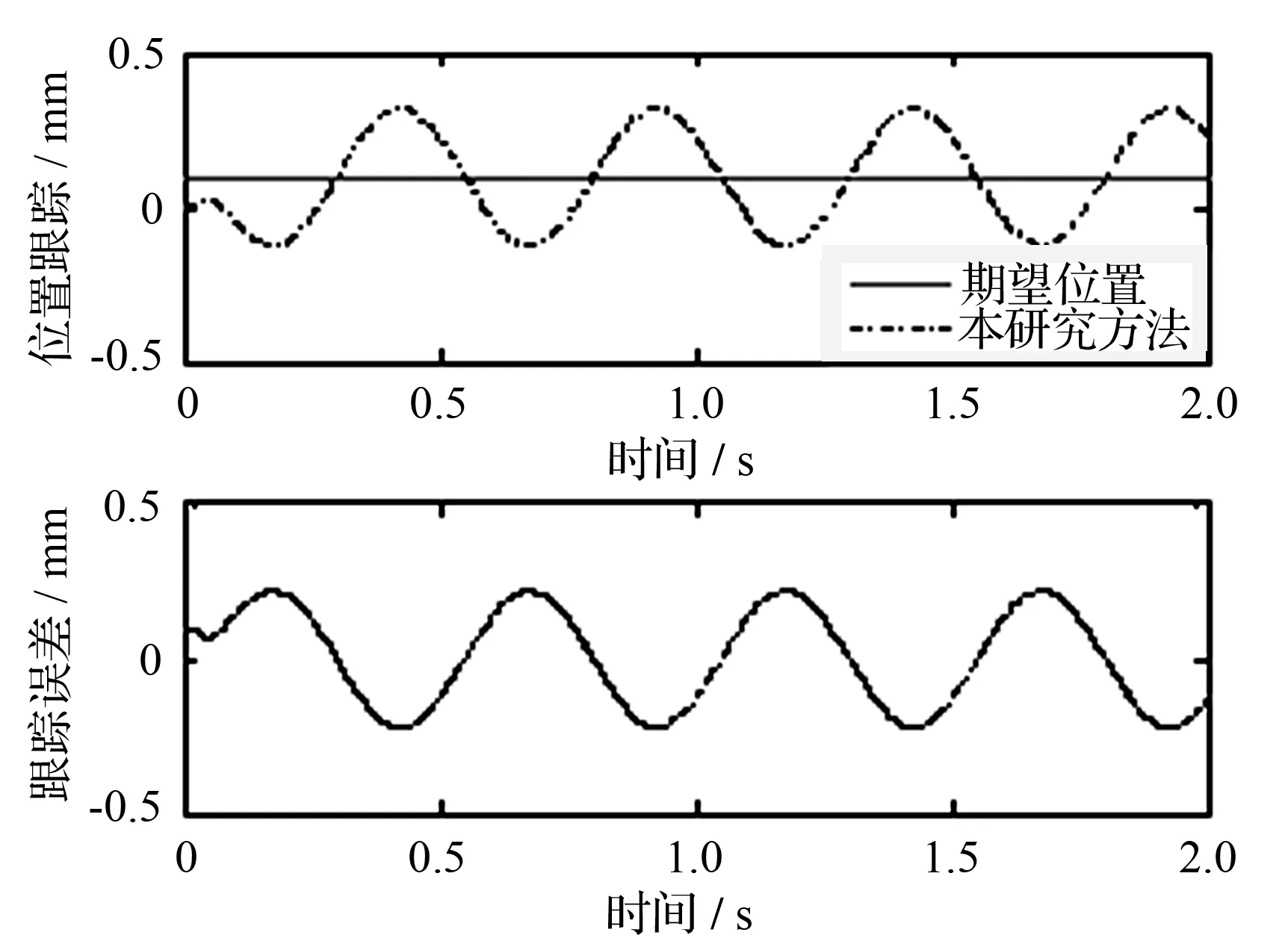
图5　不引入RBF神经网络时位置跟踪和跟踪误差

图6是利用RBF神经网络逼近外负载力干扰的效果，逼近曲线快速收敛，并且图7中逼近误差可以收敛到零附近的一个很小的领域内。逼近精度好，也可以看出运用自适应律来调整权值的效果。图8中跟踪曲线快速跟踪给定信号，无超调，跟踪误差在0.1 s内渐进收敛为零。

为了验证引入一阶低通滤波器计算中间虚拟控制量的准确性，图9将式(5)与(6)、式(8)与(9)的输出进行了对比。

图6　RBF神经网络对系统外负载力干扰逼近

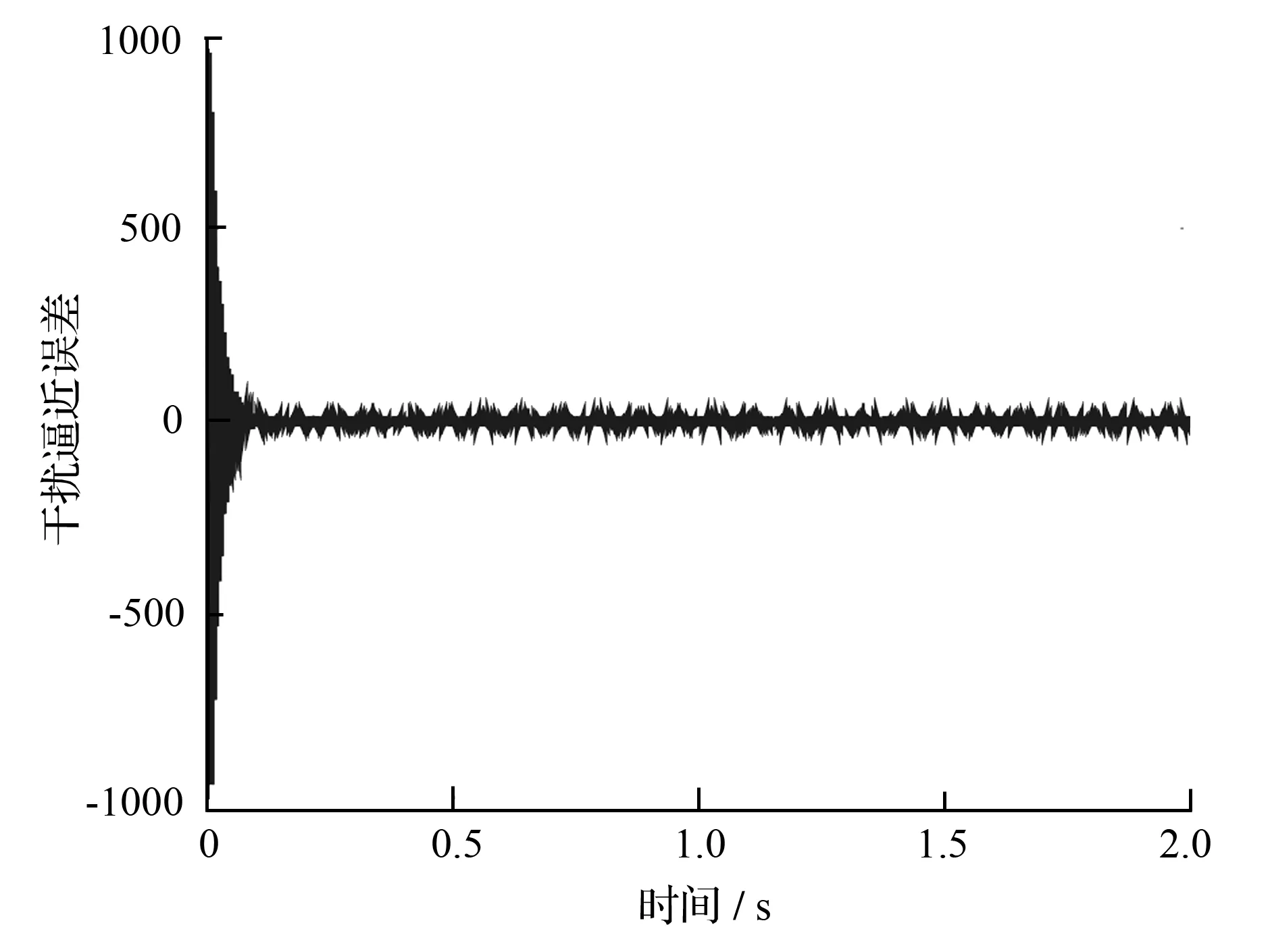
图7　RBF神经网络对系统外负载力干扰逼近误差

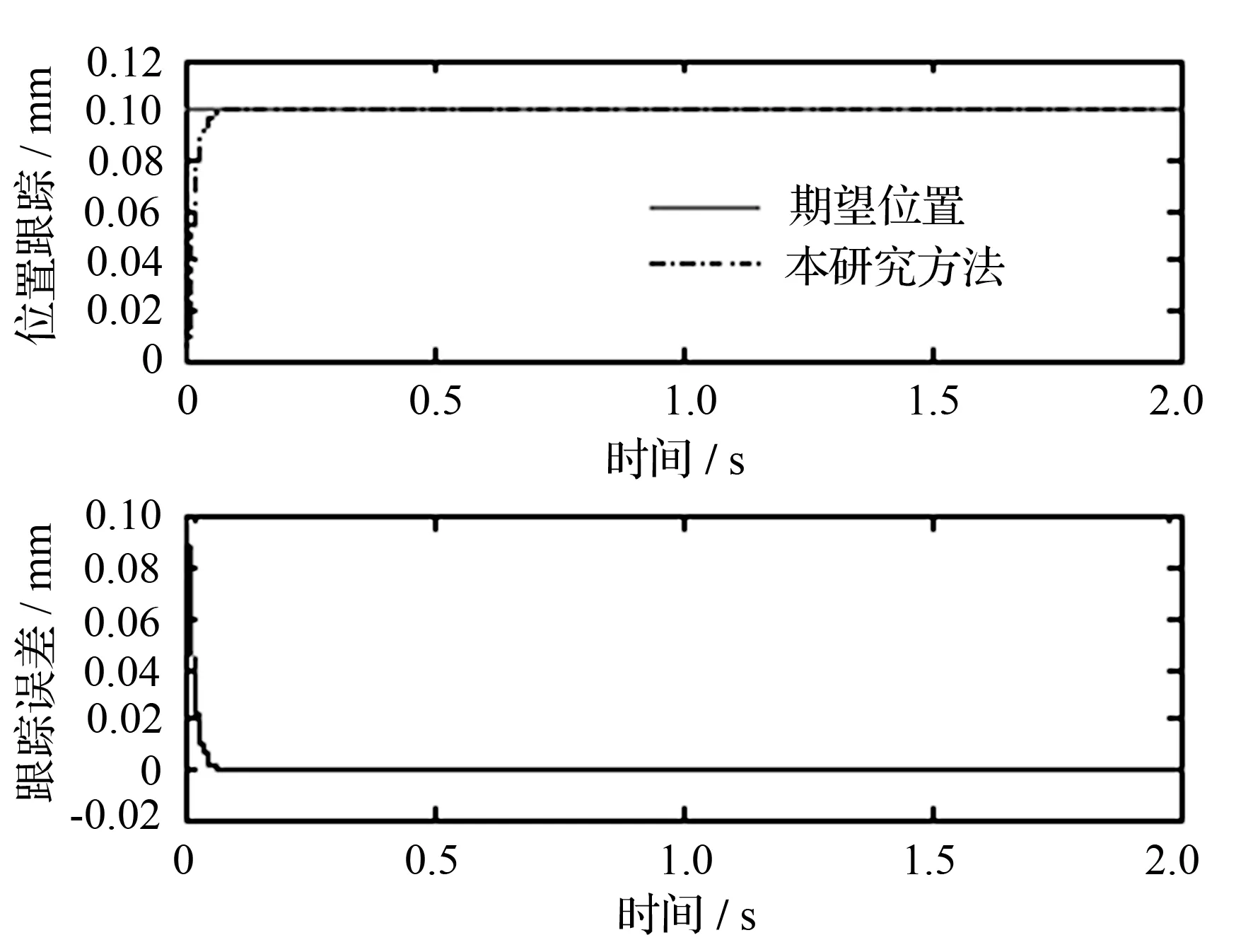
图8　本研究提出控制策略的位置跟踪和跟踪误差

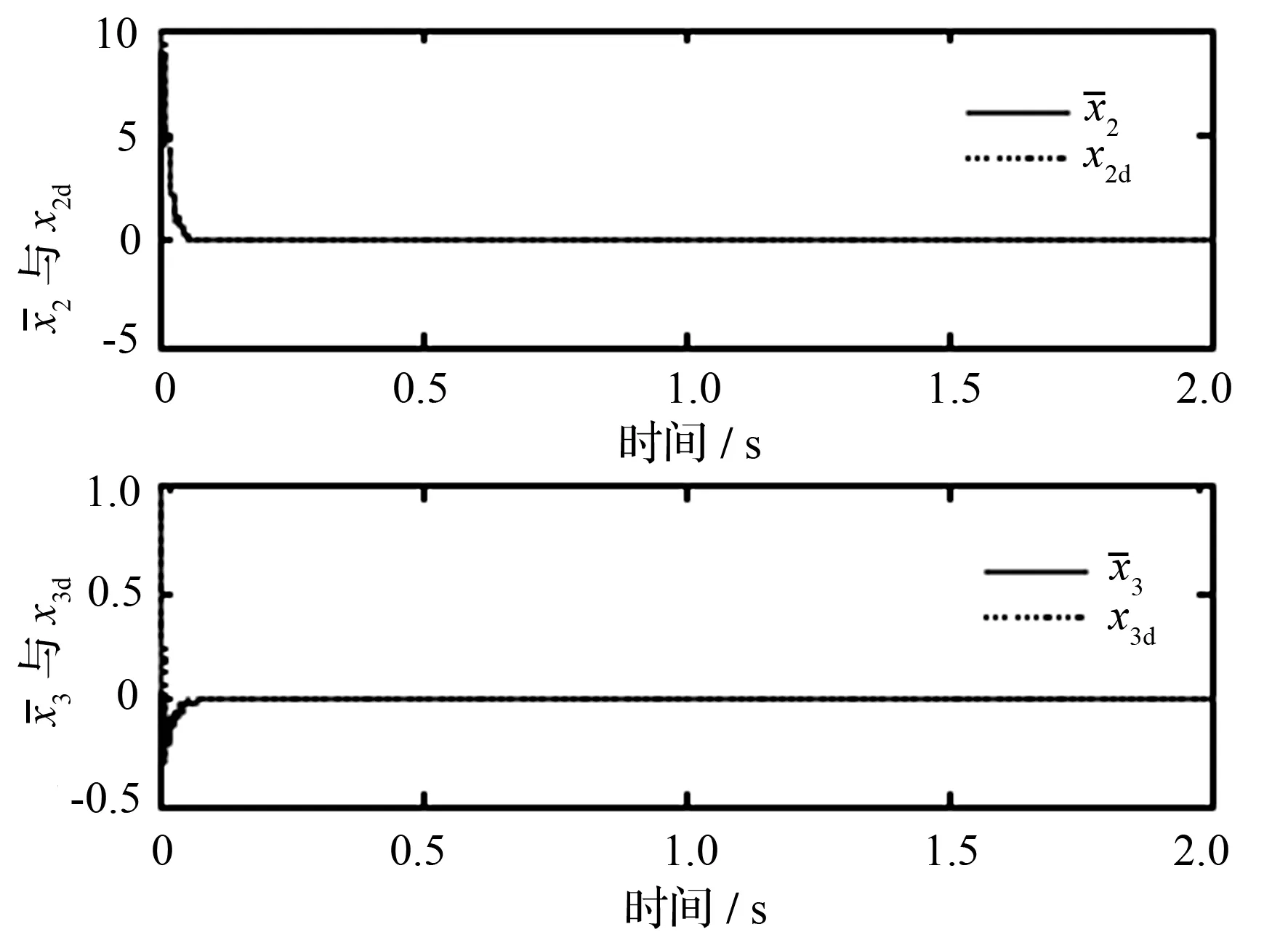
图9　一阶低通滤波器输出曲线

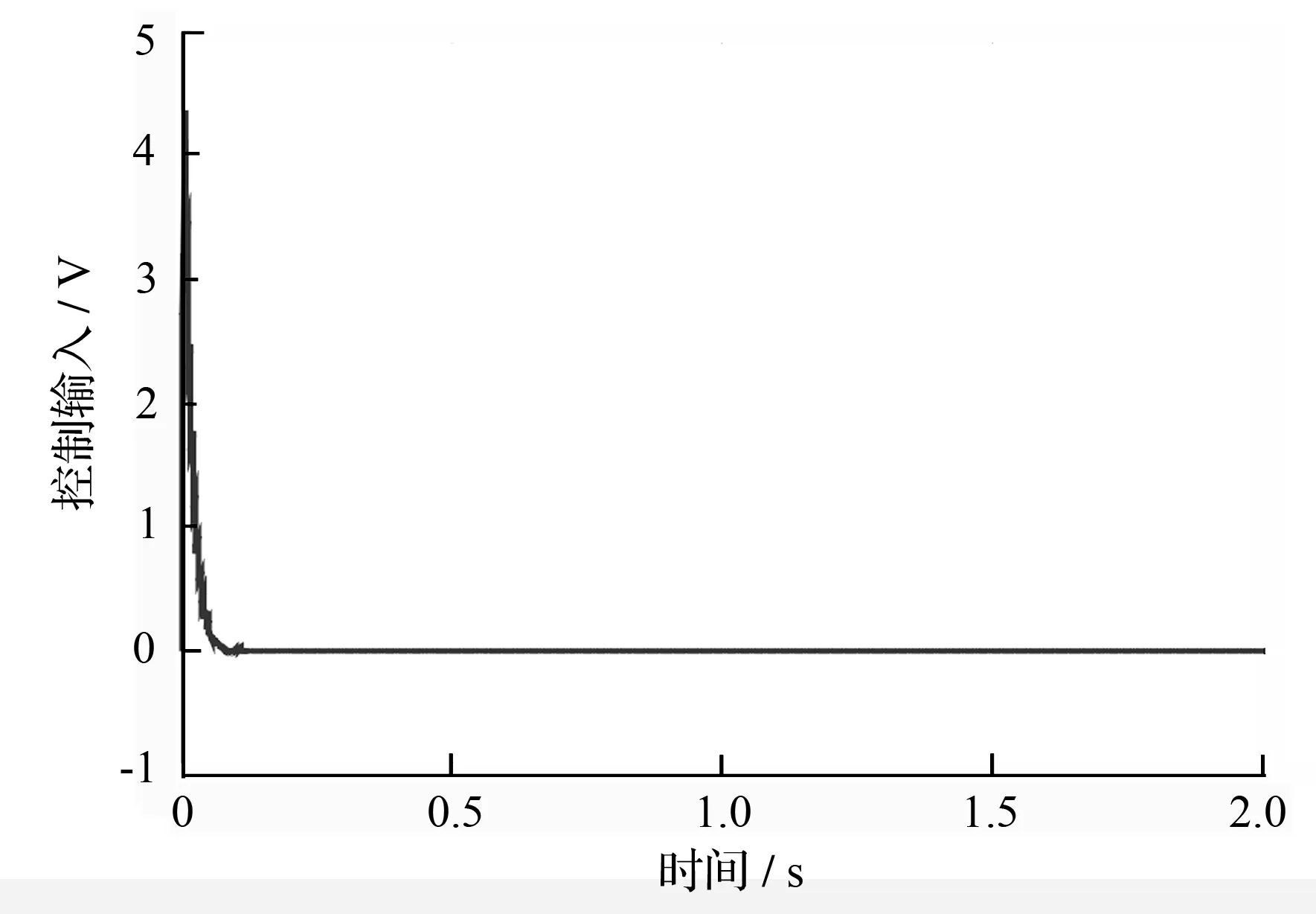
图10　MDF电液位置伺服系统控制输入曲线

控制输入曲线如图10所示，曲线较为平滑，能说明RBF神经网络逼近外负载力干扰的精度高，系统具备良好的鲁棒性；输入电压较低在5 V以下，看出系统能耗较低。

5结论

针对MDF连续热压机的电液位置伺服系统，考虑定厚段的实际工艺，提出了一种基于RBF神经网络的板厚动态面控制策略。利用RBF神经网络并辅以权值调整的自适应律，有效地逼近了热压过程中外负载力对系统产生的干扰；动态面控制器中，引入一阶低通滤波器解决了反步法中易出现的微分项膨胀问题，从而简化了控制器的设计。仿真结果表明，该控制策略使系统具备较高的控制精度、较短的收敛时间、较小的输入电压及良好的鲁棒性，从而保证了MDF达到预期的厚度精度。

参考文献

[1]许方荣.我国中密度纤维板生产现状、发展趋势与应用景[J].林产工业,2010,37(4):3-5.

[2]谭守侠,周定国.木材工业手册[M].北京:中国林业出版社,2007:200-203.

[3]王凯.木材工业实用大全之纤维板卷[M].北京：中国林业出版社,2002:235-238.

[4]欧阳琳.连续平压热压机(之二)[J].木材工业,1997,11(3):37-40.

[5]刘亚秋,朱良宽,黄晓舟.基于零相差前馈跟踪的中密度纤维板连续热压系统PID控制[J].东北林业大学学报,2014,42(6):133-136,147.

[6]邵小东,朱良宽,曹军.MDF连续平压位置伺服系统的反步控制[J].森林工程，2014,30(4):103-106，109.

[7]唐文秀,梁小伟,贾鹤鸣.连续平压机伺服位置系统自适应滑模反步控制[J].自动化与仪表,2015(3):40-43，56.

[8]邵小东.MDF连续热压机板厚控制液压系统位置跟踪控制研究[D].哈尔滨：东北林业大学,2015.

[9]梁小伟.MDF连续平压板厚控制方法研究[D].哈尔滨：东北林业大学,2015.

[10]SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. Automatic Control IEEE Transactions on,2000,45(10):1893-1899.

[11]SONG B, HEDRICK J K, KANG Y. Dynamic surface control and its application to lateral vehicle control[J]. Mathematical Problems in Engineering,2014(4):1-10.

[12]Hou Mingzhe, Liang Xiaoling, Duan Guangren. Adaptive block dynamic surface control for integrated missile guidance and autopilot[J]. International Journal of Automation & Computing,2013,26(3):741-750.

[13]刘晓东,黄万伟,禹春梅.含扩张状态观测器的高超声速飞行器动态面姿态控制[J].宇航学报,2015,36(8):916-922.

[14]Wang Dan, Huang Jie. Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form[J]. IEEE Transactions on Neural Networks,2005,16(1):195-202.

[15]邓贞贞.基于PLC的人造板连续压机热压控制系统研究[D].长沙：中南林业科技大学,2012.

[16]吴振顺.液压控制系统[M].北京:高等教育出社,2008:14-43.

[17]刘金琨.智能控制[M].3版.北京：电子工业出版社，2014:201-202.

[18]PARK J, SANDBERG I W. Universal approximation using radial-basis-function networks[J]. Neural Computation,2008,3(2):246-257.

[19]方一鸣,许衍泽,李建雄.具有输入饱和的电液伺服位置系统自适应动态面控制[J].控制理论与应用,2014,31(4):511-518.

[20]SONG B, HEDRICK J K, HOWELL A. Robust stabilization and ultimate boundedness of dynamic surface control systems via convex optimization[J]. International Journal of Control,2002,75(12):870-881.

MDF Continuous Hot Pressing Plank Thickness Dynamic Surface Control By RBF Neural Network

Zhu Liangkuan, Wang Zibo, Liu Yaqiu

(Northeast Forestry University, Harbin 150040, P. R. China)//Journal of Northeast Forestry University，2016,44(6)：68-74.

For the characteristics of medium density fiberboard continuous hot pressing process, we proposed a dynamic surface plank thickness tracking control strategy based on the RBF Neural Network, in which the external load disturbance was taken into consideration at the stage of keeping thickness. For the electro-hydraulic position servo system in the continuous hot-press, we constructed the RBF neural network to approximate the external load disturbance for the compensation of the control law, and designed an adaptive law to weights in the network. By using dynamic surface control method, first low-pass filters were applied to calculate synthetic control inputs in solving differential terms expansion in the backstepping design. An appropriate Lyapunov function was chosen to prove that all signals of the closed-loop system was semi-globally uniformly ultimately bounded and the tracking error converges to zero asymptotically. By simulation, the proposed strategy could ensure the thickness control precision effectively with strong robustness for the system process.

KeywordsMedium density fiberboard (MDF); Continuous hot pressing; Plank thickness control; RBF neural network; Dynamic surface control

第一作者简介：朱良宽，男，1978年11月生，东北林业大学机电工程学院，副教授。E-mail：zhulk@126.com。

收稿日期：2015年11月15日。

分类号TS653.6; TP183

1)国家林业局“948”项目(2014-4-46)；国家自然科学基金(31370565)；黑龙江省博士后启动基金(LBH-Q13007)。

责任编辑：戴芳天。