机械抖动偏频激光陀螺静态测角方法*

谢元平，于旭东，魏　国，龙兴武，罗　晖，黄　云，万志毅

(国防科技大学 光电科学与工程学院， 湖南 长沙　410073)



机械抖动偏频激光陀螺静态测角方法*

谢元平，于旭东，魏国，龙兴武，罗晖，黄云，万志毅

(国防科技大学 光电科学与工程学院， 湖南 长沙410073)

摘要：阐述采用机械抖动偏频激光陀螺进行静态角度测量的原理，分析测角随机误差与激光陀螺角随机游走系数、测量时间的关系，通过转台分度误差实验验证了测角随机误差公式。采用排列互比法对测角系统误差和转台分度误差进行分离。实验与理论分析表明，静态测角方法具有良好的环境适应性和稳定性，测角随机误差优于0.26″，系统误差优于1″。最后分析了进一步减小测角随机误差和系统误差的措施。

关键词：角度测量；机械抖动偏频激光陀螺；随机误差；系统误差；排列互比法；分度误差

激光陀螺是基于光学Sagnac效应的高性能角速度和角度传感器，具有很高的角度测量精度和分辨率，其在测角时可以偏心安装且具有整周自校修正标度因数等优点，可用于转台、光学编码器、多面棱体等的角度测量和校正[1-13]。早期采用四频差动激光陀螺进行角度测量[1-4]，工作转台可采用低转速的，但由于四频差动激光陀螺精度较低、温度特性差，目前其生产和应用并不普遍。大多数激光陀螺测角研究均采用速率偏频工作方式下的二频激光陀螺进行动态测角[5-9,11-13]以减小激光陀螺固有锁区导致的标度因数非线性影响，工作转台转速一般为36～3600(°)/s，此种情况下，对激光陀螺、待检体之间的输出同步精度要求较高，否则同步误差会降低测角精度。

二频机械抖动偏频激光陀螺具有零偏稳定性好、标度因数线性度高等突出优点，但其输出中不仅包含了惯性角速度，也包含了抖动偏频信号，因此并不适合动态测角。因此，对基于机械抖动偏频激光陀螺(以下简称激光陀螺)的静态测角和准动态测角方法进行了研究，讨论静态测角方法，该方法可用于转台、光学编码器、磁编码器等的角度测量和校正，且不需要激光陀螺与编码器等待检体同步输出，具有可对转台、编码器任意角位置进行检测，操作简单，环境适应性好等优点。

1原理

激光陀螺用于光学编码器、磁编码器的角度测量过程与转台分度误差测量类似，故以转台分度误差测量为例说明。如图1(a)所示,将激光陀螺安装到待检转台台面上，激光陀螺敏感轴b与转台回转轴线a基本平行,夹角γ小于1°。信号处理与记录装置对激光陀螺输出脉冲进行低通滤波以滤除抖动偏频信号，并定时记录滤波后的激光陀螺输出脉冲增量。

(a) 测角系统原理图(a) Schematic diagram of angle measurement setup

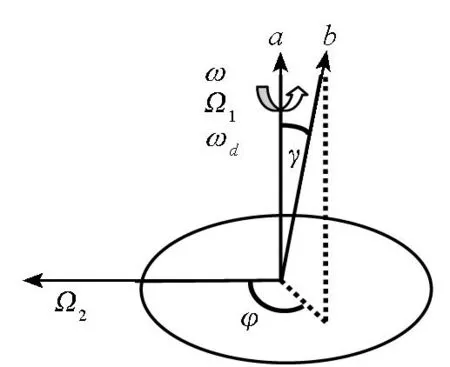
(b) 输入角速度(b) Input angular velocity图1　测角系统组成与输入角速度示意图Fig.1　Schematic diagram of angle measurementsetup and input angular velocity

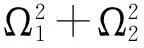
激光陀螺输出脉冲经低通滤波消除抖动偏频信号后可表示为：

υ=S[ωcos(γ)+Ω1cos(γ)+Ω2cos(φ)sin(γ)+B0]

(1)

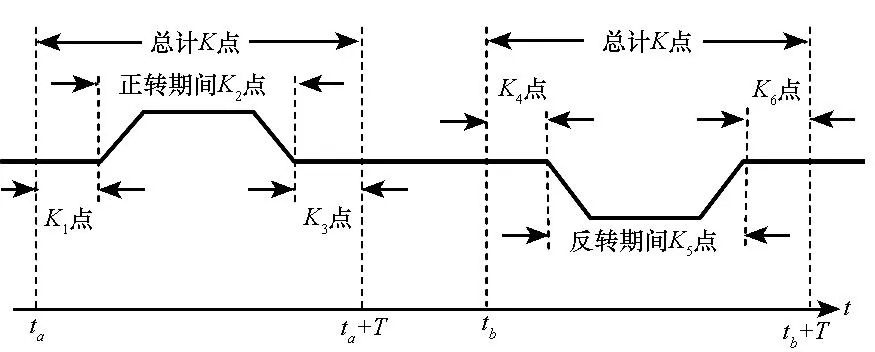
图2　单次测角激光陀螺输出脉冲增量示意图Fig.2　Gyro′s output in one turn of angle measurement

式中，S为激光陀螺标度因数，B0为激光陀螺零偏，φ为激光陀螺敏感轴在转台台面内的投影与Ω2的夹角，φ随转台角位置变化。

转台在由零位静止状态正向转动角度θ、静止、反向转动角度θ回到零位静止整个过程中，记录的激光陀螺输出脉冲增量如图2所示。图中K2与K5接近但不一定相等。

累加[ta,ta+T]期间K点数据得到该时间间隔内激光陀螺总输出脉冲数N+，N+满足：

N+=Sθcos(γ)+SB0T+SΩ1cos(γ)T+

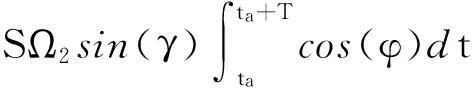
(2)

累加[tb,tb+T]期间K点数据得到该时间间隔内激光陀螺总输出脉冲数N-，N-满足：

N-=-Sθcos(γ)+SB0T+SΩ1cos(γ)T+

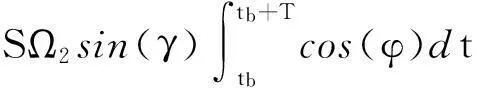
(3)

由式(2)、式(3)有：

(N+-N-)=2Sθcos(γ)+ΔE

(4)

(5)

ΔE是转台正反转过程中地球自转角速度分量Ω2sin(γ)引起的残差。 Ω2sin(γ)本身很小，例如γ为10′时，Ω2sin(γ)<0.044(″)/s。 Ω2sin(γ)的影响因转台正反转而基本对消。如累加数据时使K1和K6接近、K3和K4接近，可以进一步提升对消效果。 总之， ΔE可忽略，因此：

N+-N-=2Sθcos(γ)

(6)

类似地，转台由零位静止状态正向转动M整周、静止、反向转动M整周回到零位静止，分别累加完整包含转台正转、反转的连续K′点数据(对应时间为T′)得到N0+，N0-：

N0+-N0-=2S×360Mcos(γ)

(7)

由式(6)、式(7)有：

θ=360M(N+-N-)/(N0+-N0-)

(8)

式(8)为抖动偏频激光陀螺静态测角公式，单位为(°)。因上述测量过程中转台转过确定的角度θ且累加数据起始点均对应转台静止状态，因此不需要转台与激光陀螺同步输出，也不需要考虑低通滤波引起的陀螺输出延时，所以是一种静态测角方法。由式(8)可知，θ测量值与激光陀螺标度因数S以及轴线夹角γ的绝对值无关，因而不需要对激光陀螺标度因数S进行测量，在激光陀螺安装时也无须像光电自准直仪等常规测角方法一样进行复杂的调整。同时，θ测量值与激光陀螺零偏B0绝对值、转台台面水平状态也无关。这些特点提高了机械抖动偏频激光陀螺静态测角的检测精度，扩展了其适用范围。

2误差分析

由式(8)可得到测角误差为：

(9)

测角误差包括系统误差和随机误差。系统误差通常由激光陀螺某个参数随待测角位置的周期性变动引起，如地磁场或转台磁场导致的激光陀螺参数周期性变化[12]。测角随机误差则主要由激光陀螺的输出噪声、环境振动引起。高精度测角时对环境振动有要求，且可通过隔振措施进一步减小振动影响，因此下面给出的公式中没有包含环境振动引起的测角随机误差。

激光陀螺输出噪声主要包括角随机游走、量化噪声、偏置不稳定性、速率随机游走、速率斜坡[14]。其中量化噪声主要表现为高频成分，陀螺输出低通滤波后，量化噪声的影响可以忽略。偏置不稳定性、速率随机游走、速率斜坡只在测试时间较长时影响才不能忽略。单次测角时T和T′一般小于100s，因而对激光陀螺输出噪声只需考虑角随机游走的影响。因此，测角随机误差满足：

(10)

在多次测量某固定角度θ求其离散度时，(N0+-N0-)通常取固定的测量值，其误差表现为比例系数误差，不会影响θ测量的离散度，故测角随机误差可表示为：

(11)

式(11)为机械抖动偏频激光陀螺静态测角随机误差公式。

由式(11)可知：转台转速一定时，测角随机误差随转角增大而增大，通过适当增大转速来降低测试时间可减小随机误差；也可采用角随机游走系数N小的激光陀螺以减小随机误差。此外，对多次测量结果取平均也可减小随机误差。

由于工作在抖动偏频方式的激光陀螺角随机游走系数比工作在速率偏频方式的大，且测角时间长，因此机械抖动偏频激光陀螺静态测角随机误差范围要比环形激光动态测角仪给出的0.01″～0.2″[7, 12]要大。

3实验

按照上述方法采用激光陀螺单轴旋转惯导系统中的天向陀螺对单轴工作转台进行测试。单轴转台角位置绝对精度优于±70″、重复性优于±0.4″；测试时惯导系统置于环境振动较小的地下室，环境温度为10～30 ℃，系统与周围环境不隔振。

3.1随机误差

表1是激光陀螺工作1h、内部温度基本稳定后对转台各角位置的测量结果，测量时转台转速为5(°)/s，各位置重复测量10次。

表1　随机误差测试结果

可见，测量标准差优于0.30″，极差(测量最大值-最小值)优于0.90″。

因为对转台某个角位置进行重复测试时，激光陀螺输出噪声与转台定位重复性均会影响测量结果，因此总的随机误差为：

(12)

式中，Q为转台定位重复性误差，单位为(″)。

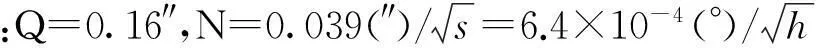
对转台上电锁定时测得的陀螺静态数据进行Allan方差[14]分析可得到陀螺量化噪声系数为0.05″，因此量化噪声对测角随机误差的影响确实可以忽略。从测量误差中减去转台定位重复性误差后，单次测角随机误差优于0.26″。

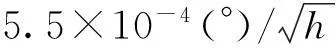
3.2系统误差

要采用更高一级的角度计量基准对激光陀螺测角系统误差进行验证是很困难的，考虑到工作转台有较好的定位重复性，故采用排列互比法进行激光陀螺和转台的互检[15-16]。

排列互比测量共进行了12个测回，每个测回测量12个角位置，测量间隔角为30°，各测回的每个角位置均只测量1次，转台转速设置为50(°)/s，测量结果见表2，表2中每一横行为1个测回，共12测回144个测量数据。在排列互比法的一个测回结束、待检转台转动至下一位置后，通常需要使陪检设备(如多面棱体、激光陀螺)反向转动。但由于激光陀螺敏感的是惯性空间的转动，其绕转台转轴转动一个角度后与转台相对位置的改变并不影响陀螺后续输出，因此可以不进行实际的反向转动。

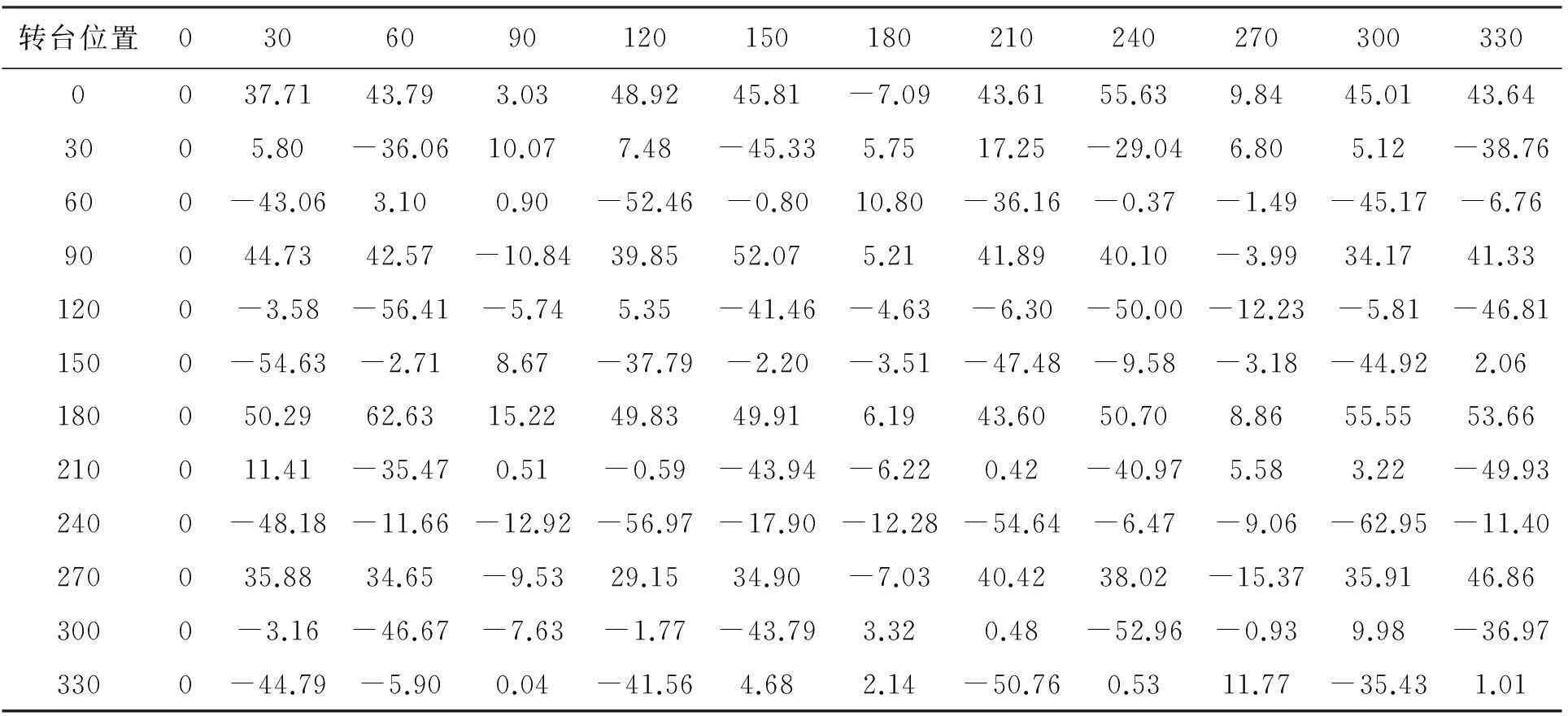
表2　排列互比测量结果

注：表2中第一行与第一列为转台位置(单位:(°))，其余为角位置误差(单位: (″))。

排列互比计算方法如下[16]：记n为测回数,各测量数据为ai,j(i,j=1,2,…,n)，则第i横行和Ri、第j竖列和Sj、第k斜行和Yk满足：

(13)

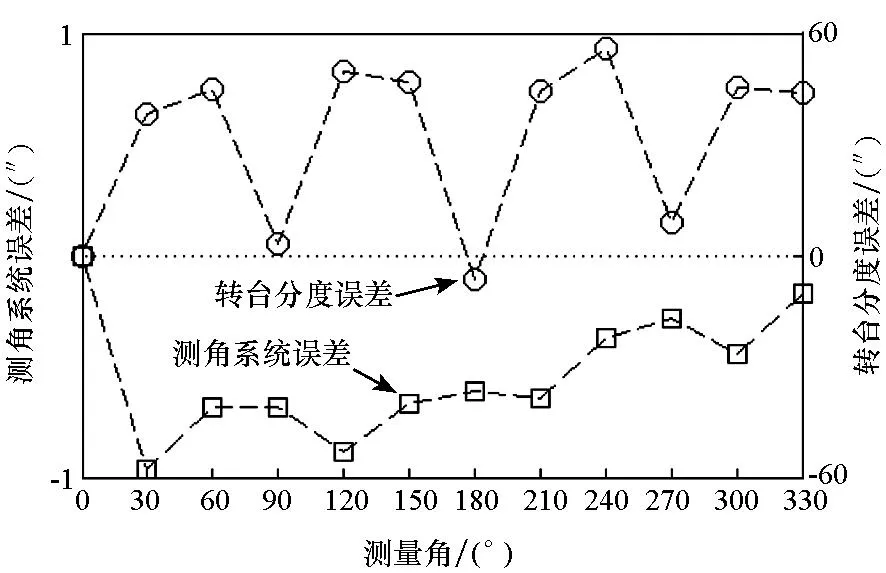
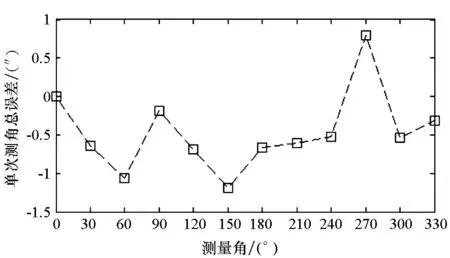
式中，ε=0(k≥i)， ε=n(k

Δαj=Sj/n

(14)

转台分度误差为：

Δβi=[(Yi-Y1)-(Ri-R1)]/2n

(15)

测量不确定度为：

(16)

式中，l=0(i+j-1≤n)，l=n(i+j-1>n)。据式(16)可得到测量不确定度σ=0.15″，它由包括转台定位重复性误差、激光陀螺测角随机误差在内的各种随机误差因素引起。

根据式(14)、式(15)得到陀螺测角系统误差和转台分度误差如图3(a)所示。

可见，测角系统误差最大值接近1″。如前所述，激光陀螺测角系统误差通常由激光陀螺某个参数随待测角位置的周期性变动引起，如地磁场或转台磁场导致的激光陀螺参数周期性变化。由于采用的旋转惯导系统天向陀螺有多层磁屏蔽，由外部磁场引起的测角系统误差理论上应该远小于1″，所以系统误差偏大的一个主要原因可能是惯导系统中存在橡胶减震环节，惯导系统在不同角位置和加速度下形变不同，相应会引入测角误差；另一个原因是所用转台定位重复性精度有限时，各测回每个角位置只进行单次测量会引入较大误差。

(a) 测角系统误差和转台分度误差(a) Angle measurement systematic errorand turntable indexing error

(b) 单次测角总误差(b) Total error of single measurement图3　排列互比法分析结果Fig.3　Analysis results of permutation intercomparison method

要减少这些误差因素以进一步验证静态测角系统误差，可将单个激光陀螺直接固联在高精度的气浮转台上，并通过多面棱体、光电自准直仪进行排列互比检测，同时采取稳定环境温度、隔离环境振动等措施。可以预见，机械抖动偏频激光陀螺静态测角系统误差将远小于1″。

将排列互比法得到的转台分度误差与表2第一行相减可得到单次测角总误差，如图3(b)所示，可见包括测角随机误差、系统误差以及转台定位重复性误差在内的总误差小于2″。

以足够小的角度间隔对转台分度误差进行测量得到分度误差表格，再根据多项式拟合、谐波分析法拟合等方法[17]进行补偿即可得到转台任意角位置的修正值。对于激光陀螺单轴旋转惯导系统，单轴转台角位置精度主要影响航向精度。利用机械抖动偏频激光陀螺静态测角方法和误差补偿技术，将激光陀螺单轴旋转惯导系统中单轴转台角位置绝对精度从原有的±70″修正至±2″以内，满足了惯导系统高精度、长航时导航要求。

3.3环境适应性测试

为验证机械抖动偏频激光陀螺静态测角方法的环境适应性，在不同测试条件下对转台90°角位置进行了测量，结果如表3。表3所有测试结果均为10次连续测量平均值，其中序号1～4，6～7转台平放，序号1～6转台转轴与陀螺敏感轴夹角γ约1′，序号1～5，7转台转速5(°)/s，序号2～7激光陀螺连续工作。

由表3可得到测试结果标准差为0.40″，极差为1.22″。实验结果表明：与光电自准直仪加多面棱体等常规测角方法相比，机械抖动偏频激光陀螺静态测角方法具有良好的环境适应性和稳定性，对陀螺内部因素如温度变化、模式跳变不敏感，对转台转速、转台放置状态、转台转轴与陀螺敏感轴夹角等外部因素也不敏感。

表3　不同测试条件下90°角位置测试结果

4结论

尽管与环形激光动态测角仪相比，机械抖动偏频激光陀螺静态测角随机误差相对较大，但由于其静态测角随机误差优于0.26″、系统误差优于1″，且静态测角方法不需要激光陀螺与待检体同步输出，其具有测角系统组成简单、环境适用性好等突出优点，可广泛用于转台、车床、光学编码器、磁编码器等的角度测量和校正。可通过选择角随机游走系数小的激光陀螺、减少测角时间、隔离环境振动、减少电磁辐射、采用高精度工作转台等措施进一步提高测角精度。

参考文献(References)[1]中国计量科学研究院环形激光课题组.四频环形激光器用于精密测角[J].物理, 1979, 8(6): 510-513.

RingLaserResearchTeamofNIM.Precisionanglemeasurementwithfour-moderinglaser[J].Physics, 1979, 8(6): 510-513. (inChinese)

[2]徐毅, 廖复中, 戴润生, 等. 环形激光精密测角[J].计量学报, 1981, 2(3): 163-168.

XUYi,LIAOFuzhong,DAIRunsheng,etal.Theringlaserfortheprecisemeasurementofangle[J].ActaMetrologicaSinica, 1981, 2(3): 163-168. (inChinese)

[3]徐毅, 廖复中, 戴润生, 等. 环形激光精密角度标准的建立与验证[J].计量学报, 1985, 6(4): 261-263.

XUYi,LIAOFuzhong,DAIRunsheng,etal.Thedevelopmentofanglestandardbyusingtheringlaseranditsverification[J].ActaMetrologicaSinica, 1985, 6(4): 261-263. (inChinese)

[4]徐毅, 廖复中, 戴润生, 等.高精度四频环形激光测角传感器[J].仪器仪表学报, 1986, 7(2): 113-118.

XUYi,LIAOFuzhong,DAIRunsheng,etal.Apreciseangletransducer—thefour-frequenciesringlaser[J].ChineseJournalofScientificInstrument, 1986, 7(2): 113-118. (inChinese)

[5]RodloffKR,StielerFM,WetzigV,etal.Highresolutiongyrosystemforpreciseangularmeasurement:USA,5408751[P]. 1995-04-25.

[6]FilatovYV,LoukianovDP,ProbstR.Dynamicanglemeasurementbymeansofaringlaser[J].Metrologia, 1997, 34(4): 343-351.

[7]AgapovMY,BurnashevMN.Errorsofmeasurementbylasergoniometer[C]//ProceedingsofSPIE, 2000, 4316: 26-30.[8]FilatovYV,AgapovMY,BournachevMN,etal.Lasergoniometersystemsfordynamiccalibrationofopticalencoders[C] //ProceedingsofSPIE, 2003, 5144: 381-390.

[9]黄宗升, 秦石乔, 王省书, 等. 光栅角编码器误差分析及用激光陀螺标校的研究[J].仪器仪表学报, 2007, 28(10): 1866-1869.

HUANGZongsheng，QINShiqiao，WANGXingshu,etal.Erroranalysisofopticalangldarencoderanditscalibrationwithringlasergyro[J].ChineseJournalofScientificInstrument, 2007, 28(10): 1866-1869. (inChinese)

[10]姚宝聚, 金世龙. 一种新数控机床旋转工作台旋转精度检测方法研究[J].中国科技信息, 2010, 2:139-140, 144.

YAOBaoju,JINShilong.Theresearchofanewmethodontherotatingprecisiondetectingofnumericcontrolmachinetool[J].ChinaScienceandTechnologyInformation, 2010, 2: 139-140, 144. (inChinese)

[11]谢启华.激光陀螺测角仪误差理论与实验研究[D].长沙:国防科学技术大学, 2011.

XIEQihua.Thetheoreticalandexperimentalstudyontheerrorsoftheringlasergoniometer[D].Changsha:NationalUniversityofDefenseTechnology, 2011. (inChinese)

[12]BurnashevMN,PavlovPA,FilatovYV.Developmentofprecisionlasergoniometersystems[J].QuantumElectronics, 2013, 43 (2): 130-138.

[13]FilatovYV,NikolaevMS,PavlovPA,etal.Non-contactmeasurementofanobject′sangularpositionbymeansoflasergoniometer[C] //ProceedingsofSPIE, 2014, 9250: 925006.[14]IEEEStd647-2006.IEEEstandardspecificationformatguideandtestprocedureforsingle-axislasergyros[S].IEEEAerospaceandElectronicSystemsSociety, 2006.

[15]EstlerWT.Uncertaintyanalysisforanglecalibrationsusingcircleclosure[J].JournalofResearchoftheNationalInstituteofStandardsandTechnology, 1998, 103(2): 141-151.

[16]孙方金.角度计量测试技术——排列互比法[J].中国计量, 1997(12): 49-51.

SUNFangjin.Anglemetrologyandtesttechnology—permutationintercomparisonmethod[J].ChineseMetrology, 1997(12): 49-51. (inChinese)

[17]KaulSK,TickooAK,KoulR,etal.Improvingtheaccuracyoflow-costresolver-basedencodersusingharmonicanalysis[J].NuclearInstrumentsandMethodsinPhysicsResearchSectionA:Accelerators,Spectrometers,DetectorsandAssociatedEquipment, 2008, 586(2): 345-355.

Static angle measurement based on mechanically dithered ring laser gyro

XIE Yuanping, YU Xudong, WEI Guo, LONG Xingwu, LUO Hui, HUANG Yun, WAN Zhiyi

(CollegeofOptoElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

Abstract：Theprincipleofstaticanglemeasurementbasedonmechanicallyditheredringlasergyrowasdescribed.Theexpressionofanglemeasurementrandomerrorwithgyro′sanglerandomwalkcoefficientandmeasurementtimewasanalyzedandverifiedbycheckingtheindexingerrorsofturntable.Thesystematicerrorofstaticanglemeasurementandtheindexingerrorsofturntablewereseparatedbyusingthepermutationintercomparisonmethod.Testresultsandanalysisshowthatthestaticanglemeasurementmethodisrobustunderpracticalenvironment,thestandarddeviationofrandomerrorislessthan0.26″andthesystematicerrorislessthan1″.Thekeytechniquesforfurtherimprovementinaccuracywereanalyzed.

Keywords：anglemeasurement;mechanicallyditheredringlasergyro;randomerror;systematicerror;permutationintercomparisonmethod;indexingerror

doi:10.11887/j.cn.201603023

收稿日期：2015-03-23

基金项目：国家自然科学基金资助项目(61503399)

作者简介：谢元平(1971—)，男，湖南新邵人，研究员，博士，硕士生导师，E-mail:xyp99999@139.com

中图分类号：TH741.2

文献标志码：A

文章编号：1001-2486(2016)03-135-06

http://journal.nudt.edu.cn