一类时变时滞系统的稳定性准则

李欢欢，姜偕富，唐超超

(杭州电子科技大学自动化学院，浙江 杭州 310018)



一类时变时滞系统的稳定性准则

李欢欢，姜偕富，唐超超

(杭州电子科技大学自动化学院，浙江 杭州 310018)

摘要：研究了一类时变时滞系统的稳定性问题.采用积分不等式法和时滞分解法，充分利用时变时滞的上界和下界等信息，构造一个新的Lyapunov-Krasovskii泛函，并使用不同的积分不等式对Lyapunov-Krasovskii泛函求导过程中所产生的积分项进行处理，得到了一个保守性更小的稳定性准则.最后通过数值实例验证了该准则的有效性.

关键词：时变时滞；积分不等式；稳定性准则

0引言

时滞现象存在于许多系统中，如制造业、电信、化工等，对系统性能有不利影响[1].一般情况下，人们主要对常时滞和时变时滞系统进行研究，但大多情况下，适用于常时滞系统的稳定性判据并不一定适用于时变时滞系统，所以，众多学者主要对时变时滞系统进行研究.为了减少已有成果的保守性，解决系统的时滞问题，使系统更稳定地工作，学者们提出了许多有效的方法，如文献[2]为减小固定权矩阵产生的保守性，在对时滞系统分析时采用了自由权矩阵法；文献[3]采用了时滞分解的方法，但过多的分割区间增加计算的复杂度和仿真时间，使系统的运行效率降低；文献[4]在构造泛函时引入了三重积分项，加入该项后并没有明显减小所得结果的保守性.上述文献的一个共同点是对泛函求导过程中产生的积分项进行处理时都使用了Jensen不等式，虽然Jensen不等式使用方便、简单，但存在一定的保守性.文献[5]引入了Wirtinger型积分不等式，在不影响所得结果保守性的前提下使用的决策变量数较少.但该方法主要用于未对时滞进行分解的情况，因此，尝试着将时滞分解法与Wirtinger型积分不等式结合使用，以得到保守性更小的稳定性准则，是一个有意义的研究问题.

本文针对一类具有时变时滞的线性系统，将时滞τ(t)分解为τ1(t)和τ2(t)两部分，充分利用时变时滞的信息构造一个Lyapunov泛函，针对泛函求导过程中所产生的不同积分项，采用不同的积分不等式进行处理，得到了一个保守性更小的稳定性准则.

1系统描述

本文中，考虑如下区间时变时滞系统：

(1)

式中：x(t)∈Rn为状态向量，A和B为已知的适当维数的系统矩阵，φ(t)∈Rn为系统的初始条件，τ(t)为系统状态时滞.满足0≤τm≤τ(t)≤τM，其中τm,τM为常数.

为了得到时变时滞系统保守性较小的稳定性准则，充分利用时滞信息，假设τ(t)=τ1(t)+τ2(t).其中0<τ1m≤τ1(t)≤τ1M,0<τm≤τ(t)≤τM，显然τ1m≤τm,τ1M≤τM.

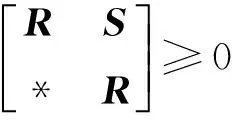
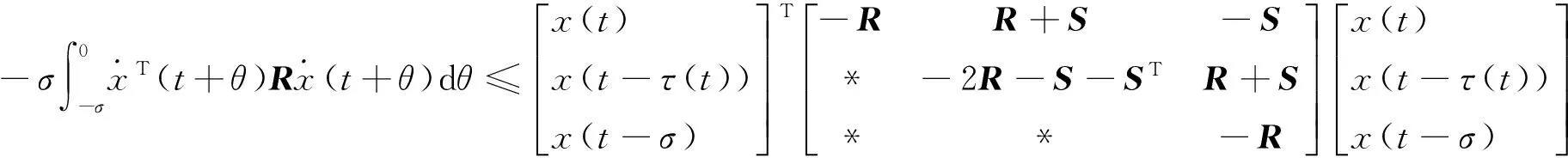
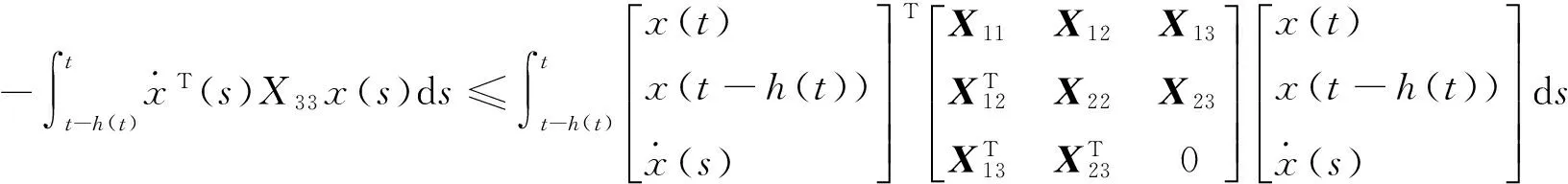
2稳定性准则

针对具有时变时滞的线性系统(1)，给出以下稳定性准则：

定理对于给定的τ1m,τ1M,τm,τM，若存在具有适当维数的矩阵P>0，Qi>0(i=1,2,3),Zj>0(j=1,2),Si(i=1,2),Xij,Yij,Zij,(1≤i≤j≤3)使得如下线性矩阵不等式成立，则式(1)所表示的系统是渐近稳定的.

(2)

(3)

(4)

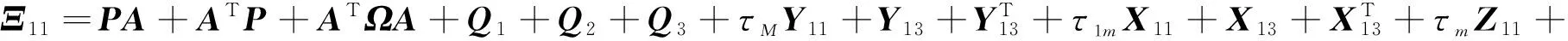
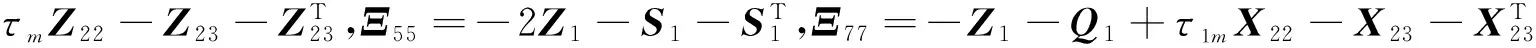
Ω=δ12Z1+δ2Z2+τ1mX33+τMY33+τmZ33,δ1=τ1M-τ1m,δ=τM-τm

证明选取如下所示的Lyapunov-Krasovskii泛函：

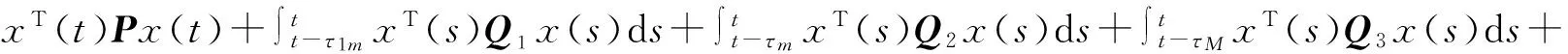
(5)

将该泛函沿式(1)所示系统对时间t求导，得：

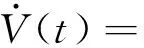
(6)

(7)

(8)

对式(6)中以下积分项采用文献[7]的方法来处理，由引理2得：

(9)

(10)

(11)

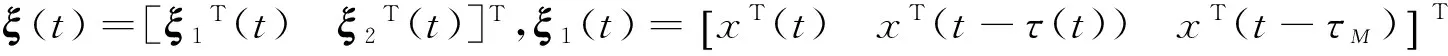
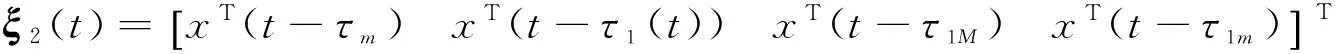
综上所述，如果定理1成立，则系统(1)是渐近稳定的.证毕.

为了充分利用时滞信息，本文将时滞区间划分成非均匀的两部分，从而更准确地估计积分区间的上下界，这样定义的泛函所得结果具有更小的保守性.对泛函求导过程中产生的交叉项进行处理时，为了减少使用Jensen不等式带来的保守性，本文采用了新的积分不等式进行处理，从而得到一个较好的结果.

3数例

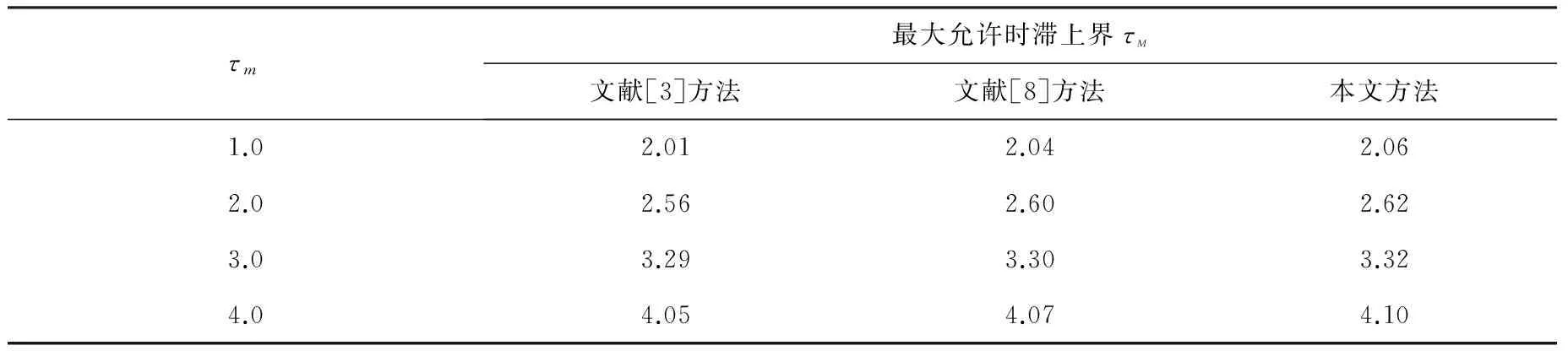
表1　3种方法得到的最大允许时滞上界比较

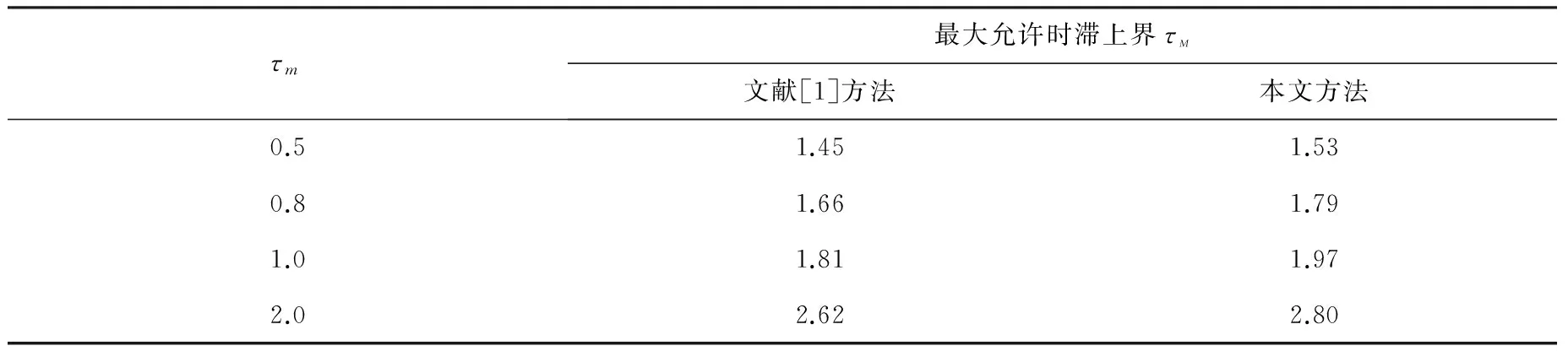
表2　2种方法得到的最大允许时滞上界比较

文献[3]没有对时滞τ(t)进行分解，文献[8]对积分项的处理采用与本文不同的不等式，但未使用时滞分解法.而本文对时滞τ(t)进行了分解，同时使用新的积分不等式对泛函求导过程中产生的积分项进行处理.由表1、2可以看出，本文将时滞分解法和不等式法结合起来使用后得到的稳定性准则保守性更小，从而说明了本文方法的有效性.

4结束语

本文研究了一类时变时滞系统稳定性问题.首先分析了先前文献中存在的问题，然后针对这些问题，将不等式法和时滞分解法结合起来使用，并在处理积分项时使用不同的引理，以线性矩阵不等式形式得到一个新的稳定性准则.比较先前部分文献，所得的稳定性准则具有更小的保守性，最后通过例子验证了该稳定性准则的有效性.

参考文献

[1]QIANW,LIT,CONGS,etal.Stabilityanalysisforintervaltime-varyingdelaysystemsbasedontime-varyingboundintegralmethod[J].JournaloftheFranklinInstitute, 2014, 351(10):4892-4903.

[2]WUM,HEY,SHEJH,etal.Delay-dependentcriteriaforrobuststabilityoftime-varyingdelaysystems[J].Automatica, 2004, 40(8):1435-1439.

[3]QIANW,LIUJ.Newstabilityanalysisforsystemswithintervaltime-varyingdelay[J].JournaloftheFranklinInstitute, 2013, 350(4):890-897.

[4]FARNAMA,ESFANJANIRM.Improvedstabilizationmethodfornetworkedcontrolsystemswithvariabletransmissiondelaysandpacketdropout[J].IsaTransactions, 2014, 53(6):1746-1753.

[5]ZHANGX,GONGC.FurtherImprovementofWirtinger-basedIntegralInequalityforSystemsWithTime-varyingDelay[C].Proceedingsofthe34thChineseControlConference.Hangzhou:IEEE, 2015:1545-1549.

[6]YANGFS,ZHANGHG,WANGYC.Anenhancedinput-delayapproachtosampled-datastabilizationofT-Sfuzzysystemsviamixedconvexcombination[J].NonlinearDynamics, 2014, 75(3): 501-512.

[7]LIUPL.Improveddelay-range-dependentrobuststabilityforuncertainsystemswithintervaltime-varyingdelay[J].ISATransaction, 2014, 53(6): 1731-1738.

[8]TANGM,WANGYW,WENC.Improveddelay-range-dependentstabilitycriteriaforlinearsystemswithintervaltime-varyingdelays[J].ControlTheory&ApplicationsIet, 2012, 6(6):868-873.

A Stability Criterion for a Class of Systems with Time-varying Delay

LI Huanhuan, JIANG Xiefu, TANG Chaochao

(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Abstract：This paper investigates a problem of time-varying delay stability criterion. By using integral inequality approach, a new Lyapunov-Krasovskii functional is established based on the information of the upper and lower bounds of time-varying delay. Different integral inequalities are adopted to deal with the integral terms of the Lyapunov-Krasovskii functional derivation and a less conservative stability criterion is obtained. Finally, a numerical example is given to examining the effectiveness of the stability criterion.

Key words：time-varying delay; integral inequality; stability criterion

DOI：10.13954/j.cnki.hdu.2016.04.011

收稿日期：2016-01-07

基金项目：浙江省自然科学基金重点资助项目(LZ13F030001)

作者简介：李欢欢(1991-)，女，河南新乡人，硕士研究生，控制科学与工程.通信作者：姜偕富教授,E-mail：jiangxf@hdu.edu.cn.

中图分类号：TP273

文献标识码：A

文章编号：1001-9146(2016)04-0052-05