基于三类代数曲线上的双线性对实现

年晓宇，游　林

(杭州电子科技大学密码与信息安全研究所，浙江 杭州 310018)



基于三类代数曲线上的双线性对实现

年晓宇，游林

(杭州电子科技大学密码与信息安全研究所，浙江 杭州 310018)

摘要：双线性对中，最常见的是Tate对，Eta对和Ate对是Tate对的变种.针对椭圆曲线y2+y=x3+x+b，其中b∈2，通过分类讨论，给出了4种情况下的Tate对和Eta对实现算法.同时，还提出了基于超椭圆曲线y2+y=x5+ax+b(其中a,b∈2)上的Tate对和Ate对实现算法，以及基于超椭圆曲线y2=xp-ax-b(其中a,b∈p)上的Ate对实现算法.为基于双线性对密码体制的研究和应用提供了一定的参考.

关键词：Tate对；Eta对；Ate对；椭圆曲线；超椭圆曲线

0引言

双线性对具有极高的安全性和很强的实用性，可用于构造复杂、安全和高效的密码协议.例如，双线性对中的Weil对可用于构造安全高效的签名方案[1]；双线性对中的Tate对可用于构造多方密钥管理方案[2-3]；将双线性对与Diffie-Hellman结合，还可以用于构造基于身份的加密方案[4].由于双线性对的计算比较复杂，如何提高其运算效率是关键问题.文献[5]表明，Tate对的运算效率高于Weil对，而Eta对和Ate对快于Tate对.本文提出了基于Tate对，Eta对和Ate对代数曲线上的双线性对算法，由于这3类曲线易于在软件中实现，因此基于这3类曲线上的双线性对算法具有一定的研究和应用价值.

1双线性对定义

1.1双线性对

定义1双线性对是如下形式的映射[6]：

e∶G×G→GT，

(1)

其中，G是一个加法群，GT是一个乘法群.

1.2Tate对

定义3设点P，Q为E上的点，fr,P是E上的有理函数，则Tate对定义如下：

er(P,Q)=fr,P(Q)(qk-1)/r.

(2)

定理1[7]设有正整数N，满足N|qk-1且r|N，则有：

fr,P(Q)(qk-1)/r=fN,P(Q)(qk-1)/N.

(3)

1.3Eta对和Ate对

定义4设有正整数T，则Eta对定义如下：

ηT(P,Q)=fT,P(Q).

(4)

定理2[7]设E是域q上的超奇异椭圆曲线，k为嵌入次数，M=(qk-1)/N，φ是一个扭映射[8].如果存在整数a，c，L，使得T=q+cN，Ta+1=LN，则有：

(ηT(P,Q)M)aTa-1=(fN,P(Q)M)L.

(5)

e(P,Q)L=fT,P(Q)c(qk-1)/N，

(6)

2曲线y2+y=x3+x+b(b∈2)上的Tate对和Eta对实现

2.1曲线y2+y=x3+x+b(b∈2)上的Tate对实现

设E:y2+y=x3+x+b为域2n上的椭圆曲线，其中b∈2，n为奇数.设P=(α,β)，Q=(x,y)为曲线E上的点.由文献[7]得嵌入次数k=4，令N=22n+1，则M=22n-1.

由文献[7]得扭映射φ(x,y)=(x+s2,y+sx+t)，其中s,t满足s2=s+1，t2=t+s.设映射φ(x,y)=(x+1,y+x)，则[2i]P=φi(α(2i),β(2i))，其中α(i)=α2i，β(i)=β2i.对i进行分类讨论可得：

设gi=h2iP(φ(Q))，把[2i]P代入h2iP可得gi，取n≡3(mod8)，由于s(i)=s+i，t(i)=t+is+τ(i)，其中i≡0,1(mod4)时，τ(i)=0；i≡2,3(mod4)时，τ(i)=1.则有：

2.2曲线y2+y=x3+x+b(b∈2)上的Eta对实现

由定理2可知，令T=q，N=22n+1，得c=0，a=2，L=1，代入式(5)可得：

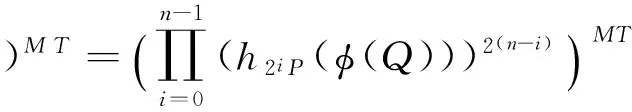
令gi=h2iP(φ(Q))，由a,b∈2，x,y,α,β∈2n，及费马定理可得：

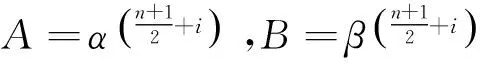
3曲线y2+y=x5+ax+b(a,b∈2)上的Tate对和Ate对实现

3.1曲线y2+y=x5+ax+b(a,b∈2)上的Tate对实现

设C∶y2+y=x5+ax+b为域2n上的超椭圆曲线，其中a,b∈2.则Jacobian群阶为：(2n)=1±2(n+1)/2+2n±2(3n+1)/2+22n.

设hP为曲线C上的有理函数，由曲线C在P=(α,β)处的切线为y=(α4+a)(α+x)+β，得hP(x,y)=(α4+a)(α+x)+β+y，于是可得基于域2n上超椭圆曲线C的Tate对的值为：(φ(Q)))2(6n-i).

gi(6n-i)=(α(i+2)+a+d)(x(-i)+w(6n-i))+β(i)+Bα(i+1)+A+y(-i)+s2(6n-i)x(1-i)+s1(6n-i)x(-i)+s0(6n-i)+b.

3.2曲线y2+y=x5+ax+b(a,b∈2)上的Ate对实现

由定义5得(fT,P(Q)kqk-1)M=(fN,P(Q))ML，可令T=q，则N=212n-1，L=1，M=1，代入可得fT,P(Q)3×211n+2=fN,P(Q).由于T=q，可得基于域2n上曲线C的Ate对的值为：fT,P(φ(Q)(φ(Q)))2(n-i).设gi=h2iP(φ(Q))，由费马定理可得：

gi(n-i)=(α(i+2)+a+d)(x(-i)+w(n-i))+β(i)+Bα(i+1)+A+y(-i)+s2(n-i)x(1-i)+s1(n-i)x(-i)+s0(n-i)+b.

4曲线y2=xp-ax-b(a,b∈p)上的Ate对实现

设曲线Cp∶y2=xp-ax-b为域pn上的超椭圆曲线，其中p为奇素数，a,b∈p，亏格g=(p-1)/2.由文献[10]知嵌入次数k=p-1，可得N=p(p-1)n/2+1，M=p(p-1)n/2-1.设P=(α,β)，Q=(x,y)为曲线上的点，则基于域pn上曲线y2=xp-ax-b的Tate对的值为：fN,P(φ(Q).

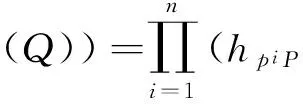
设gi=hpiP(φ(Q))，p≡1(mod4)，由a,b∈p，x,y,α,β∈q，及费马定理可得.其中(-ab-b).将gi(n-i)代入fT,P(φ(Q))可得Ate对的值.

5结束语

本文研究了基于Tate对，Eta对和Ate对代数曲线上的双线对，并通过公式化计算给出了具体的实现算法，为基于双线性对密码体制的研究和应用提供了一定的参考.下一步工作将对其他特殊曲线上的双线性对算法进行研究.

参考文献

[1]SHEN J, ZHENG W, WANG J, et al. An Efficient Verifiably Encrypted Signature from Weil Pairing[J]. Journal of Internet Technology, 2013, 14(6):947-952.

[2]CHANG S, KWON S, GAJ K. FPGA Accelerated Tate Pairing Based Cryptosystems over Binary Fields[C]//Field Programmable Technology, 2006. FPT 2006. IEEE International Conference on. IEEE, 2006:173-180.

[3]GALINDO D. Chosen-ciphertext secure identity-based encryption from computational bilinear Diffie-Hellman[M]//Pairing-Based Cryptography-Pairing 2010. Springer Berlin Heidelberg, 2010: 367-376.

[4]LE D P, TAN C H. Improved Miller’s algorithm for computing pairings on Edwards curves[J]. Computers, IEEE Transactions on, 2014, 63(10): 2626-2632.

[5]GALBRAITH S D. Supersingular curves in cryptography[M]//Advances in Cryptology—ASIACRYPT 2001. Springer Berlin Heidelberg, 2001: 495-513.

[6]CHEN C L, SHIH T F, TSAI Y T, et al. A Bilinear Pairing-Based Dynamic Key Management and Authentication for Wireless Sensor Networks[J]. Journal of Sensors, 2015：1-14.

[7]BARRETO P S L M, GALBRAITH S, HEIGEARTAIGH C O,et al. Efficient pairing computation on supersingular Abelian varieties[J].Designs,Codes and Cryptography, 2007,42(3):239-271.

[8]GALBRAITH S D, PUJOLs J, RITZENTHALER C, et al. Distortion maps for genus two curves[J]. Proceedings of A Workshop on Mathematical Problems & Techniques in Cryptology Crm, 2006, 3(1):46-58.

[9]杨怡琳.超椭圆曲线上快速标量乘算法研究[D].杭州：杭州电子科技大学,2014.

[10]施万海,游林.一类超奇异超椭圆曲线的Tate对实现[J].杭州电子科技大学学报,2013,33(6):33-36.

Bilinear Pairing Implementation Based on Three Type Algebraic Curves

NIAN Xiaoyu, YOU Lin

(InstituteofCryptographyandInformationSecurity,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Abstract：In pairings, the most common is the Tate pairing, Eta pairing and Ate pairing are the variations of the Tate pairing. For the elliptic curve y2+y=x3+x+b where b∈2, the implementation algorithms of Tate pairing and Eta pairing in four cases are given by discussing respectively. Meanwhile, the implementation algorithms of Tate pairing and Ate pairing based on the hyperelliptic curve y2+y=x5+ax+b where a,b∈2 and the implementation algorithms of Ate pairing based on the hyperelliptic curve y2=xp-ax-b where a,b∈p are proposed. It provides a reference for the research and application of the pairing-based cryptosystem.

Key words：Tate pairing; Eta pairing; Ate pairing; elliptic curve; hyperelliptic curve

DOI：10.13954/j.cnki.hdu.2016.04.005

收稿日期：2015-12-18

基金项目：浙江省钱江人才计划资助项目(2013R10071)

作者简介：年晓宇(1991-)，男，安徽蚌埠人，硕士研究生，密码学.通信作者：游林教授，E-mail：youlin@hdu.edu.cn.

中图分类号：O153.4

文献标识码：A

文章编号：1001-9146(2016)04-0020-04