基于转矩分配函数的SRM控制系统仿真

杨森峰，王家军，宋小川，高　营

(杭州电子科技大学自动化学院，浙江 杭州 310018)



基于转矩分配函数的SRM控制系统仿真

杨森峰，王家军，宋小川，高营

(杭州电子科技大学自动化学院，浙江 杭州 310018)

摘要：介绍了开关磁阻电动机转矩脉动的成因，分析了转矩分配函数法需要满足的条件及其开通角、关断角和重叠角对系统性能的影响，最后基于余弦转矩分配函数法，在Matlab/Simulink环境中对四相8/6极开关磁阻电动机进行了仿真研究.仿真结果表明，系统性能良好，从而验证了所使用转矩分配函数的有效性.

关键词：开关磁阻电动机；转矩分配函数；转矩脉动抑制

0引言

开关磁阻电动机(Switched Reluctance Motor，SRM)具有结构简单、成本低廉、启动转矩大、启动电流低、性能可靠等优点，已成为一种具有很强竞争力的调速电动机[1].但是SRM也存在着一些缺点，最显著的是在运行过程中存在较大转矩脉动，这大大限制了其应用与推广.目前，减小转矩脉动的方法之一是改进机械结构设计，另外一种方法是运用合理的控制策略.文献[2]通过优化定、转子极弧形状，从而改善相电感分布特性，降低转矩脉动.文献[3]采用直接转矩控制方法来达到抑制转矩脉动的目的.本文首先对造成转矩脉动的因素进行了分析，从研究SRM控制策略的角度介绍了基于转矩分配函数抑制转矩脉动的控制方法，并在Simulink环境中以四相8/6极SRM为控制对象运用本方法进行仿真，结果表明本控制方法能够有效地抑制SRM的转矩脉动.

1开关磁阻电动机转矩脉动的成因

SRM的内部结构如图1所示，其定、转子均为凸极结构，绕组安装在定子上，转子上无绕组，并且不是永磁体.SRM的磁链总是沿着磁阻最小的路径闭合，因此当定、转子的轴线相互不重合时，便产生磁阻力作用在转子上使其趋向磁阻最小的位置，即定、转子轴线相互重合位置，从而形成转矩.当沿着一个方向逐次导通各相定子绕组，便产生连续的转矩驱动电动机旋转.电动机各相的瞬时转矩表达式为：

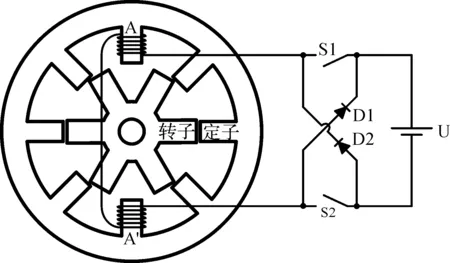
图1　SRM结构原理图

(1)

式中：Tk为第k相的瞬时转矩，θ为转子位置角，i为相电流，W′为磁共能.SRM的总转矩T为各相瞬时转矩之和，即：

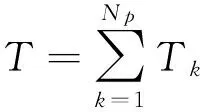
(2)

式中：NP为电动机相数.由式(1)、式(2)可以看出，SRM的合成转矩不仅与相电流有关，而且还依赖转子位置.SRM合成转矩的产生是一个较为复杂的过程，转矩脉动也是由多种因素造成的，可以概括为以下几个方面：

1)SRM定、转子所具有的双凸极结构致使电动机磁场分布具有严重的非线性；

2)在换相导通期间，当下一导通相产生的电磁转矩增大量不能够抵偿上一关断相的电磁转矩减小量时，将导致两相瞬时合成转矩不恒定，引起转矩脉动；

3)SRM的绕组电压中含有大量由功率驱动电路引起的谐波分量，谐波作用也会导致转矩脉动[4]；

4)转矩脉动还与转矩分配函数以及开通角、关断角和重叠角等参数的设定有关.

2转矩分配函数

转矩分配函数法是根据转子位置将期望总转矩分配给各相绕组，致使各相瞬时转矩之和恒定，实现平稳换相，从而抑制转矩脉动.合理的转矩分配函数不仅需要满足各相绕组的转矩之和为1.同时还需要满足各相不产生阻转矩.任一时刻，仅有一相绕组或者相邻两相绕组导通，即转矩分配条件为：

(3)

目前常用的转矩分配函数根据上升沿和下降沿波形的不同，可以分为直线型、余弦型、立方型和指数型转矩分配函数4种类型，例如余弦型和直线型转矩分配函数曲线分别如图2、图3所示.由于SRM各相绕组均为感性负载，电流的建立和关断都存在滞后现象，因此，直线型转矩分配方法的控制效果并不理想.在调速范围满足要求的条件下，当兼顾电动机的最小铜耗和最大调速范围时，优先选用余弦型转矩分配函数[5].

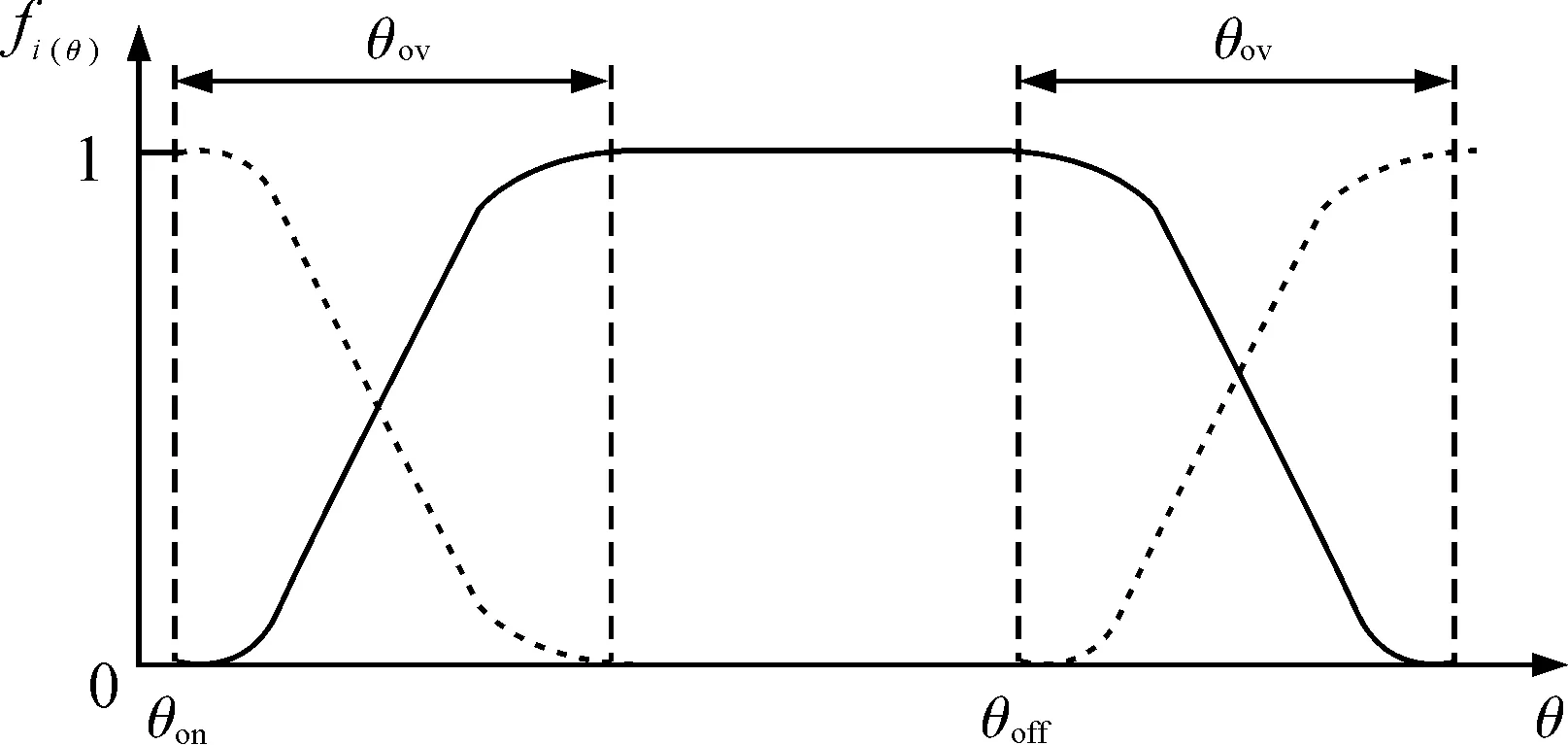
图2　余弦型转矩分配函数曲线

图3　直线型转矩分配函数曲线

将余弦型转矩分配函数定义为fi(θ)，i=1，2…，NP，则该函数表达式可以表示为：

(4)

式中：θon，θoff分别为第i相绕组的开通角和关断角，θov为第i相和第i+1相重叠导通期间的重叠角.图2中所示的各相导通过程可以分为3个阶段：

1)当θon≤θ<θon+θov时，导通相和关断相分别按照转矩分配函数逐步增加和减小.此时，电动机总输出转矩为此时导通的两相绕组输出的转矩之和；

2)当θon+θov≤θ<θoff时，电动机的总转矩由导通相单独输出；

3)当θoff≤θ<θoff+θov时，与阶段1相类似.

转矩分配函数中的参数有开通角、关断角和重叠角.如图4(a)所示，开通角的取值直接影响相电流的峰值.当开通时间提前时，相电流的峰值增大，使得电动机的转速与输出功率增加，但是相电流的脉动也随之增大，致使转矩脉动增大.以四相8/6极SRM为例，研究表明其开通角设定在3°～8°范围时，相电流的脉动最弱[6].为了使电动机具有较大的输出功率，在保证系统稳定运行的前提下，应使开通角略微提前.如图4(b)所示，关断角的取值虽然对相电流的最大值影响不大，然而对导通时间有影响，引起电流有效值的变化，从而影响输出功率.为了使电动机具有较大的输出功率，关断时间应尽量延后，但过大的关断角会使相电流延续到电感下降区，造成阻转矩的产生[7].重叠角θov的取值是由开通角和关断角共同确定的，其必须满足下式要求：θov≤θT/2-θoff.对于四相8/6极SRM，开通角和重叠角之和必须小于15°，考虑到重叠角对电动机铜耗和调速范围的影响，其重叠角的取值范围为4°～8°.

图4　开关角对绕组电流的影响

3转矩分配函数法的仿真实现

本文在Matlab/Simulink环境中，以四相8/6极SRM作为控制对象，基于余弦转矩分配函数搭建了仿真模型，如图5所示.仿真系统的绕组阻值转动惯量和阻尼系数等参数的初始化赋值，如表1所示.仿真系统采用双闭环控制，外环通过PID控制器实现速度调节，根据给定转速和反馈转速求出转速误差nerror，将其作为PID控制器的输入，输出为期望总转矩Tref；系统的内环为转矩环，由转矩分配函数控制各相的输出转矩.将外环的期望总转矩Tref与反馈的转子位置θ作为转矩分配模块TSF的输入，通过转矩分配模块计算出功率变换器Converter中的开关控制信号G1与各相的期望转矩Ti.根据四相8/6极SRM转矩特性测试实验的数据建立转矩-角度-电流特性(T-θ-i)关系表，并用其计算转矩估计值Te.Switch模块内的滞环比较单元通过比较Ti与Te求出功率变换器的开关控制信号G.

图5　基于转矩分配函数法的四相8/6极SRM仿真模型

参数名称初始值绕组阻值/Ω0.025转动惯量/(kg·m2)0.0025阻尼系数/(N·m/r)0.002最大磁链/(V·s)0.27最小/最大电感/mH2/60电源电压/V220

为了检测系统的抗干扰能力，本文分别进行了2组仿真实验，第1组仿真的给定转速为500r/min，负载转矩设定为1N·m，波形如图6所示.第2组仿真在第1组的基础上给电动机1个负载扰动，即系统运行到0.04s时将负载转矩由1N·m增加至1.5N·m，并于0.07s时取消扰动，仿真波形如图7所示.图6(a)系统的输出转速波形，可以看出电动机转速保持在给定值500r/min.图6(b)为系统的总转矩保持在1N·m，可见在换相期间各相输出转矩之和基本保持恒定，能够实现以较小误差跟踪参考值.图6(c)为相电流波形，可见相电流波形平滑，未出现较大峰值.对比2组的转速波形，可以看出，本文提出的仿真模型能够较好地实现速度跟踪.对比2组仿真的转矩波形可知，当负载转矩出现扰动时，转矩波形仍然平稳，脉动较小.综上所述，系统设定的转矩分配函数合理，本文提出的仿真模型不仅能够有效地抑制转矩脉动并且具有较好的抗干扰能力.

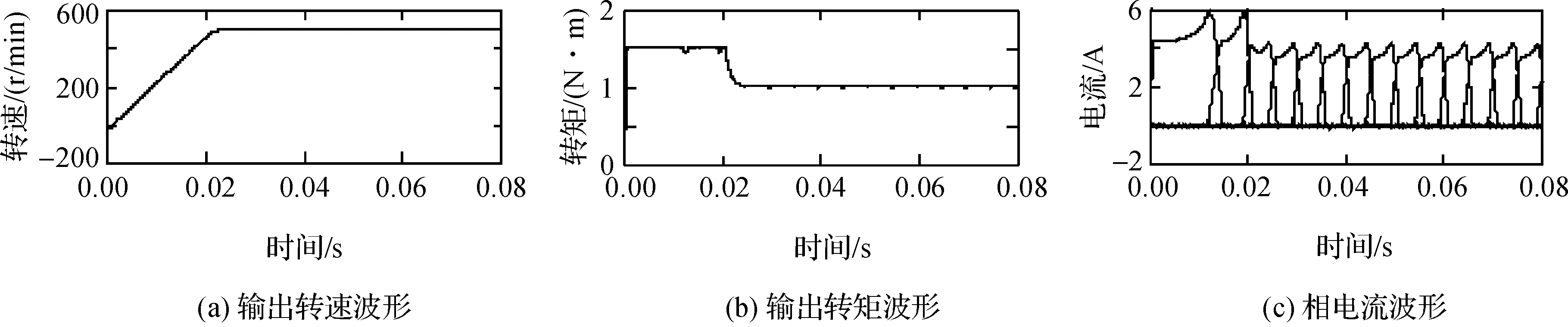
图6　第1组仿真波形

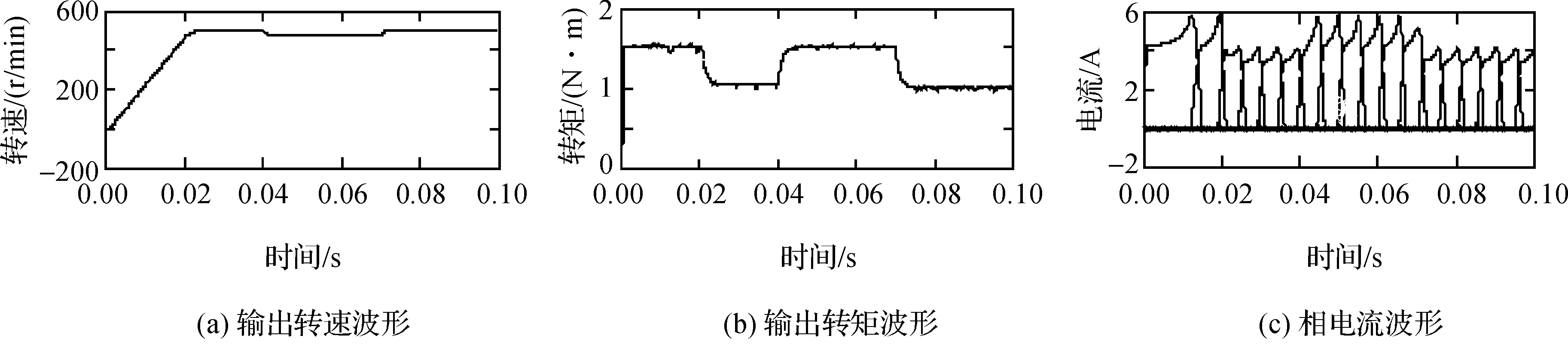
图7　第2组仿真波形

4结束语

本文在分析转矩分配函数方法的基础上，利用余弦转矩分配函数，搭建了以四相8/6极SRM为控制对象的仿真模型，实现了SRM速度和转矩双闭环控制.结果表明，控制系统性能良好，能够有效抑制电动机的转矩脉动.本文仅对SRM的转矩分配函数法进行了初步的研究，下一步将在此基础上对各种转矩分配函数的性能差异和优化转矩分配函数设计等方面进行研究.

参考文献

[1]王宏华．开关型磁阻电动机调速控制技术[M]．北京：机械工业出版社，1999：181-186．

[2]SAHIN C, AMAC A E, KARACOR M, et al. Reducing torque ripple of switched reluctance machines by relocation of rotor moulding clinches[J]．IET Electric Power Applications，2012，6(9)：753-760．

[3]俞枭辰，王家军，宋小川.基于Simulink的8/6极开关磁阻电动机的直接转矩控制仿真[J].机电工程，2013，30(3)：333-338.

[4]SCHRAMM D S, WILLIAMS B W, GREEN T C. Torque ripple reduction of switched reluctance motors by phase current optimal profiling[C]//Power Electronics Specialists Conference, 1992. PESC′92 Record, 23rd Annual IEEE. Toledo：IEEE, 1992: 857-860.

[5]XUE X D，CHENG K W E，HO S L．Optimization and evaluation of torque-sharing functions for torque ripple minimization in switch reluctance motor drives[J]．Power Electronics，IEEE Transactions on，2009，24(9)：2076-2090．

[6]SAHOO S K, PANDA S K and XU J X．Indirect torque control of switched reluctance motors using iterative learning control[J]．Power Electronics，IEEE Transactions on，2005，20(1)：200-208．

[7]吴红星．开关磁阻电动机系统理论与控制技术[M]．北京：中国电力出版社，2010：30-35．

Simulation of Switched Reluctance Motor Based on Torque Sharing Function

YANG Senfeng, WANG Jiajun, SONG Xiaochuan, GAO Ying

(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Abstract：The main cause of switched reluctance motor torque ripple is introduced in this paper. The conditions of setting torque sharing function and the influence of the turn-on angle, the turn-off angle, and the overlap angle for the system performance are analyzed. On the basis of one set cosine torque sharing function, a control simulation model for a four-phase 8/6 pole switched reluctance electric motor is built up in Matlab/Simulink environment. The stable operations prove that the torque sharing function is availability.

Key words：switched reluctance motor; torque sharing function; torque ripple suppression

DOI：10.13954/j.cnki.hdu.2016.04.009

收稿日期：2015-12-17

基金项目：国家自然科学基金资助项目(61273086)

作者简介：杨森峰(1987-)，男，河南新乡人，硕士研究生，电机控制.通信作者：王家军教授，E-mail：wangjiajun@hdu.edu.cn.

中图分类号：TM352

文献标识码：A

文章编号：1001-9146(2016)04-0040-05