一道奥数竞赛题的推广*

●李春玲

(海安县实验中学　江苏南通　226600)



一道奥数竞赛题的推广*

●李春玲

(海安县实验中学江苏南通226600)

摘要：依据微分泰勒中值定理确定的在开区间(a,b)内具有二阶连续导数的函数f(x)存在的凹凸性，对第3届IMO的一道竞赛题进行了合理地扩充,证明了2个优美的不等式，从而揭示了解决此类型不等式的一般化方法.

关键词：内切圆；导数；泰勒中值定理

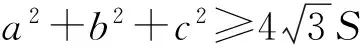
(第3届IMO试题)

笔者将这一不等式加以推广，证明了以下2个优美的不等式．

定理1在△ABC中，记a，b，c为其边长，S为其面积，k为任意给定的正整数，则

当且仅当a=b=c时，不等式取到等号．

显然，当k=2时，该不等式即为例1中的不等式．

定理2在存在内切圆的凸n边形中，设a1,a2,…,an为其各边长，S为其面积，k为任意给定的正整数，则

当且仅当a1=a2=…=an时，不等式取到等号．

为了证明上述2个定理，先证明以下3个引理．

引理1设f(x)在开区间(a,b)内存在连续的二阶导数f″(x)，其中x1,x2,…,xn∈(a,b),则

1)当f″(x)>0时，

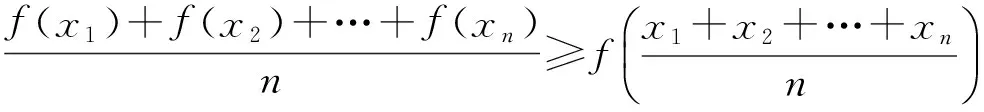
当且仅当x1=x2=…=xn时，不等式取到等号．

2)当f″(x)<0时，

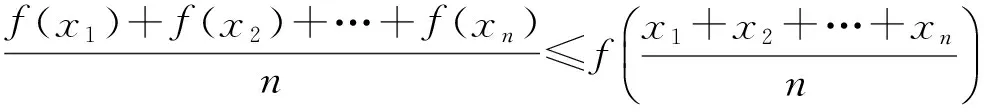
当且仅当x1=x2=…=xn时，不等式取到等号．

…

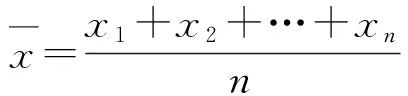
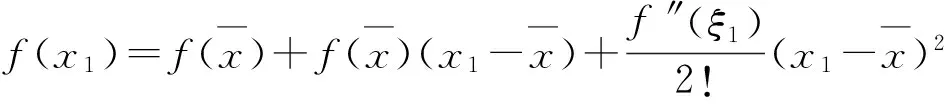
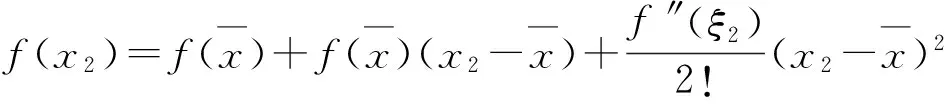
将上述n个式子的2边分别相加，即得

1)当f″(x)>0时，x∈(a,b)，由泰勒中值定理可知，上述每个中值ξi亦必属于开区间(a,b)，从而必有f″(ξi)>0，于是

即

因此，当且仅当x1=x2=…=xn时，不等式取到等号．

同理可证第2)小题.当f″(x)<0时，x∈(a,b)，

当且仅当x1=x2=…=xn时，不等式取到等号．

引理2设有n个正数，x1,x2,…,xn,k为任意给定的正整数，则

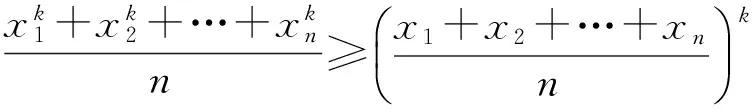
证明当k=1时，显然成立.当k≥2(其中k∈N)时，考察函数f(x)=xk，x∈(0,+∞)，易求得f″(x)=k(k-1)xk-2，从而f″(x)>0，x∈(0,+∞).由引理可得

即

当且仅当x1=x2=…=xn时，不等式取到等号．

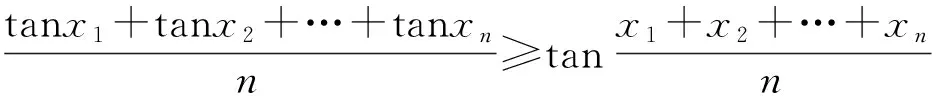
当且仅当x1=x2=…=xn时，不等式取到等号．

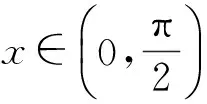
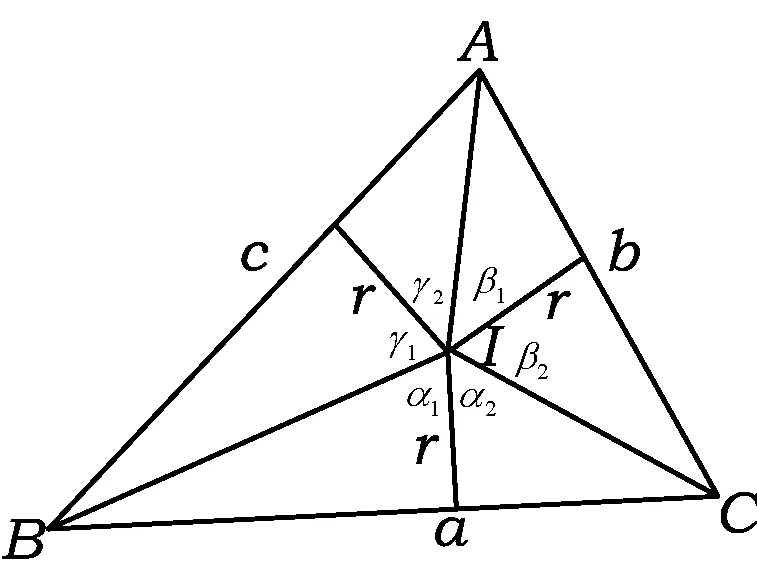
图1

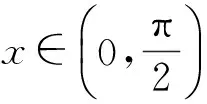
定理1的证明如图1所示，设△ABC内切圆的圆心为I，内切圆半径为r，则

从而

于是

a+b+c=r[(tanα1+tanα2)+(tanβ1+tnaβ2)+(tanγ1+tanγ2)],

由引理3，得

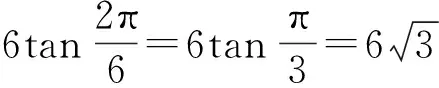
于是(a+b+c)2=r2[(tanα1+tanα2)+(tanβ1+tanβ2)+(tanγ1+tanγ2)]2≥

(1)

(2)

知

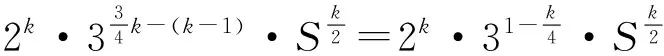
显然，欲使不等式取到等号，必须而且只须不等式(1)和不等式(2)均取到等号．

根据引理2的证明可知，若k≥2(其中k∈N)，则不等式(2)取到等号的充要条件是a=b=c；若k=1，则不等式(2)结论平凡．但由于不等式(1)取到等号的充要条件是a=b=c，因此，不等式(2)当且仅当a=b=c时取到等号．

值得指出的是:例1有多种简洁明快的证法，但是这些证法只限于三角形，难以推广到有内切圆的凸n边形情形(其中n≥3,n∈N)．笔者给出的定理1的证明显然给出了例1的新证法，更重要的是此证法不难推广到一般情形，即用完全类似的方法可以完成定理2的证明．

参考文献

[1]IMO中国国家集训队教练组.数学奥林匹克试题集锦[M].上海：华东师范大学出版社，2010.

[2]邓东皋.数学分析简明教程(上册)[M].北京：高等教育出版社,2006.

修订日期：*收文日期：2016-03-17；2016-04-26

作者简介：李春玲(1975-)，女，江苏南通人，中学一级教师.研究方向：数学教育.

中图分类号：O122.3

文献标识码：A

文章编号：1003-6407(2016)07-48-03