钛合金筒形件轧-旋成形研究进展

郭 靖，詹 梅，杨 合

（西北工业大学材料学院 凝固技术国家重点实验室，陕西西安710072）



钛合金筒形件轧-旋成形研究进展

郭 靖，詹 梅，杨 合

（西北工业大学材料学院 凝固技术国家重点实验室，陕西西安710072）

摘 要：钛合金筒形件具有轻质、高强、耐腐蚀等优点，在航空、航天和兵器领域有着广泛的应用与需求。针对目前的钛合金筒形件成形制造工艺难以满足大直径薄壁长筒形件的高效、低成本制造要求，提出了一种环轧-旋压（轧-旋）成形工艺制造钛合金筒形件的方法。在轧-旋成形工艺中，坯料历经环轧线接触与旋压点接触下的连续局部加载增量成形和显著的不均匀变形，其变形过程复杂，微观组织不均匀，容易发生破裂，影响筒形件的成形质量。为此，基于两相钛合金自洽模型和Oyane韧性准则，建立了耦合损伤的轧-旋宏微观仿真模型，研究了TA15钛合金筒形件轧-旋过程中的宏观变形行为、微观组织和损伤破裂演化规律。发现工件经轧-旋成形后，外层应变较大，中间层和内层基本相同；工件温度沿壁厚由内到外逐渐降低；α晶粒尺寸外层最小，内层和中间层相差不大；α相体积分数沿壁厚由内到外逐渐降低；工件内表面在环轧后的旋压过程中，由于正应力三轴度以及高应变速率的共同作用，最易发生破裂。

关键词：钛合金；环轧-旋压；有限元；微观组织演化；损伤演化

第一作者：郭 靖，男，1990年生，博士研究生

1 前 言

钛合金以其密度小、耐高温、耐腐蚀等诸多优异的特性，已成为航空、航天和兵器领域不可缺少的结构材料［1-5］。由该类材料制造的大直径薄壁筒形件具有轻质、高强的特性，在航空、航天和兵器领域有着广泛的应用，如喷气飞机的喷管、火箭壳体、鱼雷外壳等［6-9］。由于此类构件大都是在极端使役环境下工作，因此对其可靠性、制造完整性以及精度提出了越来越高的要求，这就给现有的制造工艺带来了新的难题和挑战。

钛合金在室温下塑性差、强度高，且材料导热率低、切削性能差，是典型的难变形材料［10-11］。目前的钛合金大直径薄壁筒形件的成形方法有:①切削成形。该方法工艺简单，但生产效率低，材料浪费严重；由于切削容易导致薄壁筒形件变形，因此切削构件精度低［12］。②卷焊。卷焊得到的是有焊缝的非匀质管。由于钛合金弹性模量小，卷圆的钛合金筒形件的型面尺寸精度难保证，且存在大的焊接应力［13］。③拉拔或环轧。该方法只适合生产径厚比较小的筒形件零件［14］。可以看出，上述成形工艺皆存在不足，难以满足大直径薄壁长筒形件高效、低成本的制造要求。

流动旋压同样是一种制造钛合金大直径薄壁筒形件的成形方法［15］。采用该方法制得的筒形件精度高，材料利用率和机械性能均优于机械加工。但该方法制造的筒形件内径受到毛坯尺寸的限制，难以满足各种非标内径筒形件的需求，因此工艺柔性不高，且制造周期较长。考虑到环轧是一种制造不同尺度环件的成形方法［14］，具有生产周期短、工艺柔性高、制造的环件尺寸精度高、力学性能好等优点。因此，本文作者综合了流动旋压和环件轧制的成形特点，提出了一种环轧-旋压（轧-旋）成形工艺［16-18］。该工艺首先通过环轧实现筒形件的直径增大和壁厚减薄，从而得到大直径的筒形件旋压毛坯，随后通过旋压来实现高度增加和壁厚的进一步减薄，最终得到成形性优良的钛合金大直径薄壁长筒形件，其工艺流程如图1所示。轧-旋成形工艺综合考虑了从筒形件毛坯制备到筒形件最终成形的整个工艺过程，结合了流动旋压和环件轧制两种成形工艺的优点，具有少无焊缝、对设备吨位要求低、生产周期短、工艺柔性高、集成度高、近净成形等特点，因此在钛合金等难变形材料大直径薄壁长筒形件的高效、低成本成形制造方面具有很好的应用前景。

图1 轧-旋过程示意图Fig.1 Process of rolling-spinning

轧-旋成形过程是一个多工步、多场、多模具、多边界相互耦合作用下的高度非线性过程。在其成形过程中，钛合金筒形件要经历复杂的热成形历史和大的不均匀塑性变形，导致其微观组织不均匀。同时由于钛合金本身塑性差、对裂纹敏感，损伤破裂也就成为钛合金筒形件轧-旋成形的主要缺陷（图2）。因此，研究钛合金筒形件轧-旋成形过程中的宏观变形行为、微观组织演变及损伤演化规律，对于提高钛合金筒形件轧-旋成形质量具有重要意义。

图2 筒形件裂纹Fig.2 Fracture in tube blank

2 研究思路与方法

由于轧-旋成形是线接触和点接触动态约束下的连续局部塑性成形过程，是涉及材料、几何和边界非线性的复杂过程，因此，基于理论、经验和反复试验的方法难以满足对该过程数字化、高技术化发展的需求。而计算机建模仿真优化与理论分析及实验研究有机结合的方法，能模拟现实成形，将大量反复试验在计算机上完成，可以比理论和实验做得更全面、更深刻、更细致，同时可以进行一些理论和实验暂时还做不到的研究，已成为研究与发展先进精确塑性成形技术，高质量、低成本、短周期、自主创新地实现塑性成形产品开发的强有力工具。

因此，本文工作以计算机数值模拟仿真为主，并与实验研究相结合，以TA15钛合金筒形件轧-旋成形为研究对象，先建立耦合损伤的轧-旋成形宏微观一体化模型，然后采用该模型开展轧-旋成形过程的宏观变形行为、微观组织和损伤演化规律研究。

3 筒形件轧-旋成形有限元模型的建立

3.1 轧-旋成形宏观有限元建模

筒形件轧-旋成形包括环轧成形，转移过渡以及旋压成形过程，是一个集温度、材料与边界非线性为一体的过程。本文基于有限元软件Abaqus/Explicit的Dynamic，Temp-disp热力耦合模块，建立了TA15钛合金筒形件轧-旋全过程模型，如图3所示［17］。其中，模具包括驱动辊、芯辊、导向辊以及芯模和旋轮，均简化为解析刚体。将TA15钛合金筒坯设为变形体，并选取六面体八节点热力耦合单元（C3D8RT）对其进行网格划分，同时采用网格自适应技术。鉴于轧-旋成形存在环轧、转移过渡及旋压3个分析步，在一次性建模中，不同分析步之间坯料与模具的精确装配难以实现。因此，提出采用多工步连续分析技术来实现轧-旋全过程建模，即通过定义初始状态场变量进行数据传递，实现了各个工步间数据的传递，最终实现了轧-旋全过程数据的无缝连接。

图3 轧-旋全过程模型Fig.3 Finite element model of rolling-spinning process

3.2 微观组织预测模型

为预测轧-旋全过程中的微观组织演化规律，根据图4所示的自洽模型流程图，开发了用于预测环轧及旋压成形过程中的组织演变规律的VUMAT子程序［19］。基于图5所示扩散模型流程图，开发了用于预测转移过渡过程的组织演变规律的VUMAT子程序［20］。

图4 自洽模型流程图Fig.4 Flow chart of self-consistent model

3.3 损伤预测模型

为预测轧-旋全过程的损伤演化规律及破裂现象，基于Oyane准则建立了适用于轧-旋全过程的韧性准则（式1）。采用弹性预估-塑性校正策略的隐式本构积分算法，开发了相应的VUMAT子程序。

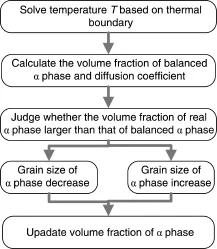
图5 中间过渡过程扩散模型流程图Fig.5 Flow chart of diffusion model of transition process

3.4 耦合损伤的轧-旋成形宏微观一体化建模及验证

基于Abaqus软件的子程序接口，将微观组织预测模型和损伤破裂预测模型嵌入到轧-旋成形宏观模型中，建立了耦合损伤的轧-旋成形宏微观模型。采用该模型，可以分析轧-旋全过程的宏观变形行为，预测组织演变及损伤演化规律。通过分析筒形件内外径的圆度、壁厚均匀性与直线度，验证了宏观模型的正确性［17］。通过与热压缩实验中的初生α相晶粒尺寸对比，验证了微观组织预测模型的可靠性［18］。通过单个单元变形验证了损伤断裂预测模型的可靠性［17］。上述结果表明，本文所建立的耦合损伤的轧-旋成形宏微观一体化模型是可靠的。

4 轧-旋全过程变形行为

采用耦合损伤的轧-旋成形宏微观模型，选取了坯料径向及内、中和外侧节点（图6），研究揭示了轧-旋成形的宏观变形行为、组织和损伤演化规律。

4.1 宏观变形行为

4.1.1 应变场分布与变化

图6 坯料径向路径及内、中和外侧节点示意图Fig.6 Schematic of radial path and inner，center and outer nodes of blank

研究获得了TA15钛合金轧-旋全过程中的等效塑性应变的分布与变化，如图7、8所示［18］。由图7可以看出，环轧后环件内侧的等效塑性应变最大，外侧其次，中部最小，如图7a所示。这是由于环件的内、外表面与轧辊直接接触，中部离轧辊距离较远。而内侧应变较外侧大，则与由环轧工艺参数所决定的环件内外侧的进给量分配有关。初始时，内、外表面的进给量基本相同，随着轧制过程的进行，环件的内半径和外半径逐渐增大，环件外表面进给量与内表面进给量比值逐渐减小，相当于外表面的进给量相对于内表面的进给量逐渐减小，因此内侧应变量更大［21-22］。由于转移过渡是个静态的过程，因此该过程中的应变基本不变，如图7b所示。经过旋压变形后，旋轮工作区应变显著增大，且应变沿壁厚方向由外到内逐渐减小（图7c）。

图7 轧-旋全过程中的等效塑性应变分布:（a）环轧后；（b）转移过渡后；（c）旋压后Fig.7 Distributions of equivalent plastic strain in rolling-spinning process:（a）after rolling，（b）after transition，（c）after spinning

由图8所示的沿轧-旋件径向的等效塑性应变分布可以看出，沿环轧件厚度由内到外，应变呈先减小后增加的趋势，内侧应变较外侧的大，且最大值约为最小值的2倍左右；旋压后，沿工件厚度由内到外，应变呈现缓慢增大再急剧增大的趋势，最大应变甚至达到最小应变的4倍以上。

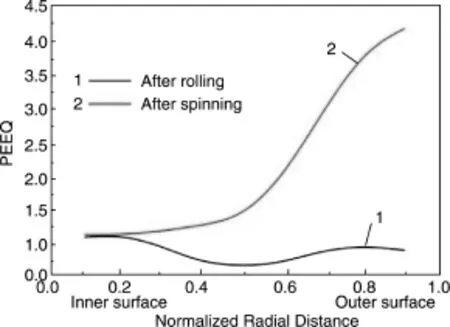
图8 沿工件径向的等效塑性应变分布Fig.8 　Distributions of equivalent plastic strain along radial direction of workpiece

4.1.2 应变速率场分布与变化

研究获得了TA15钛合金轧-旋全过程中的应变速率的分布与变化，如图9和图10所示［18］。由图9可以看出，环轧后，仅与轧辊接触的区域的应变速率较高，且坯料截面上内外表层的应变速率要比中间层高，如图9a所示。截面上内外层的应变速率不是对称分布，这是因为芯辊和驱动辊的直径不同，所形成的孔型形状也有所不同，从而导致内外层应变速率不是对称分布［23］。转移过渡过程的应变值基本无变化，因此应变速率也无变化，如图9b所示。工件经历后续旋压后，旋轮的前角和圆角区直接与工件接触，使其发生变形，因此该处的应变速率较大，如图9c所示。由图10所示的工件内侧、中部和外侧节点（图6所示）的应变速率在轧-旋过程中的变化可以看出，在环轧阶段，内外层的应变速率较大，中间层应变速率较小。到了旋压阶段，工件外侧的应变速率较大，是环轧时最大应变率的3到4倍，这说明旋压是高应变速率下的塑性变形。旋压时中间层的应变速率比内层大，说明旋压有利于改善中间层的变形。

图9 轧-旋全过程中的应变速率分布:（a）环轧后；（b）转移过渡后；（c）旋压后Fig.9 Distributions of strain rate in rolling-spinning process:（a）after rolling，（b）after transition，（c）after spinning

图10 内、中和外层的应变速率在轧-旋过程中的变化Fig.10 Variations of strain rate in inner，center and outer zones in rolling-spinning process

4.1.3 温度场分布与变化

研究获得了TA15钛合金轧-旋全过程中的温度的分布与变化，如图11和图12所示［18］。由图11可知，环轧后，工件内侧温度最高，中部次之，外侧最低，如图11a所示。这是因为经历环轧后，内侧应变量更大，热效应也更明显；加之，由于内侧只与芯辊接触，因此热传导损失热量较少，温升相对明显。中部应变量虽小，但由于与轧辊和外界环境都不接触，因此热量损失较少，故温度整体有所上升。外侧应变量比内侧小，而且其还与驱动辊和导向辊均接触，再加上与外界接触面积最大，热量损失最多，故温度最低。经历转移过渡后（图11b），由于环轧后工件内侧温度最高，因此其与外界环境温差较大，热对流和热辐射损失的热量多，而且其与工件内部之间也会进行热传导，因此温度下降较快。工件中部，主要是与周围基体间进行热传导，由外到内损失热量越来越小，因此在截面处形成了芯部温度较高的环形温度带。端部棱角区与外界环境的相对接触面积较大，同样降温明显。旋压后（图11c），工件内侧由于直接与温度较低的芯模接触传热，故温度迅速降低。而外侧旋轮工作区域由于作用面积小，应变较大，应变速率高，塑性变形产热明显，加之旋轮与工件间的摩擦作用，导致工作区域温升较高。未变形区和已变形区由于热量损失，温度下降。由沿工件径向的温度分布（图12）可以看出，经历环轧和转移过渡后，温度下降，沿径向温度分布较均匀。经历旋压变形后，内侧温度进一步降低，外侧温度升高，径向温度梯度增大，达到300℃左右。

图11 轧-旋全过程中的温度分布:（a）环轧后；（b）转移过渡后；（c）旋压后Fig.11 Distributions of temperature in rolling-spinning process:（a）after rolling，（b）after transition，and（c）after spinning

4.2 微观组织演化规律

4.2.1 初生α相体积分数分布与变化

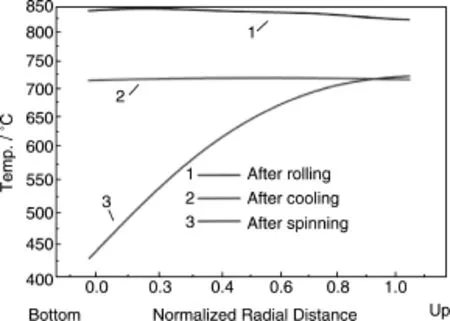
图12 沿工件径向的温度分布Fig.12 Distributions of temperature along radial direction of workpiece

鉴于初生α相的含量及分布对TA15钛合金构件的性能影响很大［24-25］。以初生α相的含量及晶粒尺寸为代表，研究揭示了TA15钛合金轧-旋全过程中的微观组织演化规律，如图13和14所示［18］。由图13可以看出，温度越高，初生α相体积分数越低，变化也越明显。这是由于本文轧-旋全过程中初生α相的体积分数分布与变化是通过自洽模型和扩散模型预测得到的。在自洽模型和扩散模型中，初生α相的体积分数分布与变化是温度的函数［19-20］。因此，轧-旋全过程中初生α相体积分数的分布与温度场分布密切相关。环轧后，靠近内侧区域的α相体积分数最低，外侧区域的最高（图13a），这与变形过程中的热量转化和传递有关。进入转移过渡阶段后，工件整体初生α相体积分数升高，且内外层α相体积分数分布均匀（图13b），这与冷却过程温度场变化情况一致。旋压后（图13c），在旋压工作区表面与旋轮直接接触的区域，初生α相体积分数降低明显，这是因为在旋轮的高速碾压和摩擦作用下，坯料表面温升明显；在坯料内表面，初生α相体积分数升高，这是因为该区域与芯模接触，温度下降明显所致。从图14可以看出，环轧后，初生α相体积分数由内到外逐渐增加；经过转移过渡过程后，初生α相体积分数整体升高且沿径向分布均匀；旋压后，初生α相体积分数沿径向由内向外逐渐减小。

图13 轧-旋全过程中的初生α相体积分数分布与变化:（a）环轧后；（b）转移过渡后；（c）旋压后Fig.13 Distributions of volume fraction of α phase in rolling-spinning process:（a）after rolling，（b）after transition，and（c）after spinning

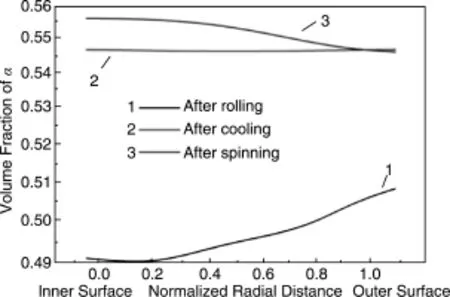
图14 沿工件径向的初生α相体积分数分布Fig.14 Distributions of volume fraction of α phase along radial direction of workpiece

4.2.2 初生α相晶粒尺寸分布与变化

研究获得了TA15钛合金轧-旋全过程中的初生α相晶粒尺寸的分布与变化，如图15和图16所示［18］。由图15可知，环轧后，初生α相晶粒尺寸相对初始坯料晶粒尺寸（11μm）整体呈下降趋势，工件内外侧晶粒尺寸比中部的小（图15a）。这说明在环轧过程中与变形相关的动态破碎机制在晶粒尺寸的演变过程中起主导作用［20］。环轧时，坯料不断通过芯辊和驱动辊之间所形成的宽度逐渐减小的孔型，剪切作用明显，晶粒得到细化。在转移过渡过程中，影响晶粒尺寸的主要因素是晶粒的静态长大，该过程坯料温度降低，平衡相体积分数增大，β相向α相转变驱动力增大，α相沿晶界析出并长大。但经过中间冷却过程后晶粒尺寸总体长大不明显，如图15b所示。这是因为平衡相体积分数在高温条件下对温度比较敏感，环轧结束后坯料最高温度为865℃，在该温度范围内平衡相体积分数随温度的变化不够明显，扩散驱动力较小同时温度对扩散系数也有影响，随着温度降低，扩散系数变小，故晶粒尺寸长大不明显［26］。旋压后，工件中部和内侧的应变虽然相对较小，但其晶粒也得到了不同程度的细化，理论上动态破碎机制导致的细化最为明显，如图15c所示。由图16可以看出，轧-旋过后外侧晶粒尺寸最小，内侧和中部晶粒尺寸相近。

图15 轧-旋全过程中的初生α相晶粒尺寸分布与变化:（a）环轧后；（b）转移过渡后；（c）旋压后Fig.15 Distributions of grain sizes of α phase in rolling-spinning process:（a）after rolling，（b）after transition，and（c）after spinning

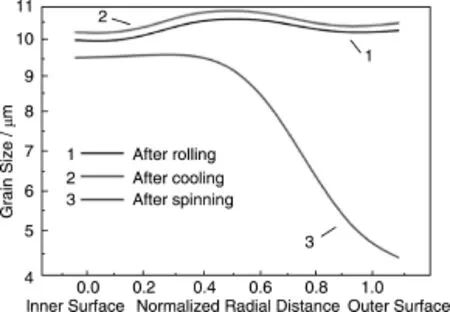
图16 沿工件径向的初生α相晶粒尺寸分布Fig.16 Distributions of grain sizes of α phase along radial direction of workpiece

4.3 损伤演化规律

4.3.1 应力三轴度分布与变化

研究获得了TA15钛合金轧-旋过程中的应力三轴度的分布与变化，如图17所示［17］。环轧时，轧制区的内外表面区域受到三向压应力，平均应力为负值，且绝对值比较大，此时材料处于压应力状态，材料的塑性较好，不容易发生断裂。轧制区的上下端区域由于受到较大的周向拉应力，应力三轴度大于0，此时材料处于拉应力状态，有利于材料内部空穴的生长，材料容易发生断裂［27］（图17a中相应轴截面示意图中的框选区域）。旋压时，旋压区的外表面区域，由于旋轮的挤压受到三向压应力，应力三轴度为负值；旋压区内表面大部分区域的应力三轴度为负，但还有部分区域的应力三轴度大于零（图17b中相应局部放大图中的红色框选区域）；旋压区的周向区域（除旋压区之外）由于受到附加的三向拉应力，应力三轴度为正。

图17 轧-旋全过程中的应力三轴度分布:（a）环轧；（b）旋压Fig.17 Distributions of stress triaxiality in rolling-spinning process:（a）rolling and（b）spinning

4.3.2 损伤分布与变化

研究获得了TA15钛合金轧-旋全过程中的损伤值的分布与变化，如图18所示［17］。研究发现，环轧时筒形件上下端的损伤值C比较大，内表面区域的损伤值C最小，并且小于零，外表面和内部的损伤值C介于两者之间，如图18a所示。由Oyane损伤理论可知，损伤值C的积累是由材料的塑性变形量以及其在塑性变形中应力状态共同决定的［28］。轧制区的上下端受到较大的周向拉应力，应力三轴度大于零，损伤的累积就会比较快。而轧制区的内外表面区域，虽然发生了较大的塑性变形，但是应力三轴度小于零，可以减缓损伤的累积。位于其他区域的材料，虽然应力三轴度比较大，但是基本不发生塑性变形，所以也不会发生损伤。旋压时筒形件损伤值C较大的区域位于内表面区域，呈环状分布；并且该环状区域随着旋轮位置向前移动，也不断向前移动，如图18b所示。旋压区外表面区域受到三向的压应力，应力三轴度为负值；在旋压区内表面区域，有应力三轴度大于零的区域，该区域在旋压区外表面材料的变形牵扯下产生协调变形，从而积累一定的损伤。

图18 轧-旋全过程中的损伤值C分布:（a）环轧后；（b）旋压后Fig.18 Distributions of damage values C in rolling-spinning process:（a）after rolling and（b）after spinning

研究获得了TA15钛合金轧-旋过程中的损伤值C与损伤阈值Cf的比值D/Cf的分布与变化，如图19～21所示［17］。由图19可以看出，环轧后，损伤比值D的分布与其损伤值C的分布是有所差别的。环轧时虽然上下端的损伤值C比较大，但是沿周向几乎呈均匀分布；而环轧的损伤比值D只和轧辊接触区域的上下端比较大（图19a）。这是因为，轧制区的应变速率比较高，损伤阈值Cf相对来说比较小，故而轧制区的上下端的损伤比值D比较大。旋压后，损伤比值D最大值的区域是旋压区的内表面区域（图19b），这是因为，对整个内表面区域而言，只有旋压区的应变速率较大，旋压区的损伤阈值Cf才能相对比较小，因此，内表面位置是后续旋压成形的危险位置。在旋压结束时，损伤比值D已经超过1，达到了1.065，说明内表面区域已经出现破裂。

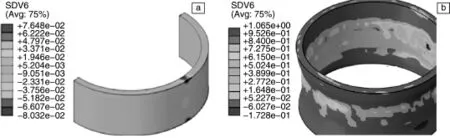
图19 轧-旋过程中的损伤比值D分布:（a）环轧后；（b）旋压后Fig1.9 Distributions of relative damage values D in rolling-spinning process:（a）after rolling and（b）after spinning

由图20所示的环轧件损伤值C和损伤比值D分布图可知，不同区域损伤值C与损伤比值D分布却是不同的，相对于内层和外层，中间层的损伤值C和损伤比值D较大。已轧区中间层的损伤值C最大，但损伤比值D却较小；而轧制区中间层的损伤值C并不是最大，但损伤比值D却最大；这是因为轧制区中间层处于变形区，应变速率相对于已轧区中间层较大，使得该处最易破裂。由图21所示的旋压件损伤值C和损伤比值D分布图可知，不同区域损伤值C与损伤比值D分布同样是不同的，相对于中间层和外层，内层的损伤值C和损伤比值D较大。旋压过程中内层的损伤值C和损伤比值D都是最大的，表明该处最易破裂。

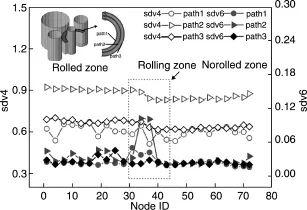
图20 环轧件损伤值C和损伤比值D分布Fig.20 Distributions of damage values C and relative damage values D in rolled tube

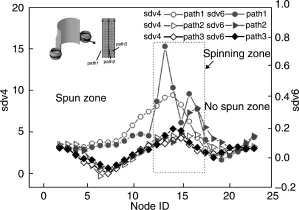
图21 旋压件损伤值C和损伤比值D分布Fig.21 Distributions of damage values C and relative damage values D in spun tube

5 结 论

高性能、轻量化构件是航空、航天和兵器等高产业发展永恒追求和目标。精确塑性成形是实现该类构件的短流程、低成本成形成性一体化的主要途径。然而，该类构件采用的轻质高强但难变形的材料，所采用的大型化、整体化和薄壁化结构及其成形过程中的多因素耦合作用导致此类材料极难实现其高性能、短周期、低成本精确成形。为此，本文综合环轧和旋压工艺的成形特点，发展提出了轧-旋成形新工艺，并研究揭示了钛合金筒形件轧-旋过程中的宏观变形行为、微观组织和损伤破裂演化规律。主要研究结论如下:

（1）基于Abaqus平台，建立了耦合损伤的轧-旋全过程宏微观变形分析三维有限元模型，为实际轧-旋过程的宏微观变形调控与优化奠定了基础。

（2）环轧-旋压成形过程后，工件外层应变最大，中间层和内层基本相同；应变速率在工件与芯辊和旋轮接触区最高，其他区域应变速率基本为0；工件温度沿壁厚方向由外到内逐渐降低。晶粒得到细化，外侧晶粒尺寸最小，内侧和中部晶粒尺寸相近；初生α相体积分数沿壁厚方向由外到内逐渐降低。应力三轴度在内表面区域大于零，损伤累积较快，因此工件内表面区域最易发生损伤。

参考文献References

［1］ Chen G，Ren C，Qin X，et al.Materials&Design［J］，2015，83:598-610.

［2］ Fan X G，Yang H.International Journal of Plasticity［J］，2011，27（11）:1 833-1 852.

［3］ He D，Zhu J C，Lai Z H，et al.Materials&Design［J］，2013，46:38-48.

［4］ Yang L，Wang B，Liu G，et al.Materials&Design［J］，2015，85:135-148.

［5］ Zhao J，Ding H，Zhao W，et al.Computational Materials Science ［J］，2014，92:47-56.

［6］ Zoghi H，Arezoodar A F，Sayeaftabi M.Materials&Design［J］，2013，47:234-242.

［7］ Xu W，Shan D B，Wang Z L，et al.Transactions of Nonferrous Metals Society of China［J］，2007，17（6）:1 205-1 211.

［8］ Xu Wenchen（徐文臣），Shan Debin（单德斌），Chen Yu（陈宇），et al.Forging&Stamping Technology（锻压技术）［J］，2008，33（3）:56-59.

［9］ Li Xinhe（李新和），Yang Xinquan（杨新泉），Wang Yanfen（王艳芬）.Forging&Stamping Technology（锻压技术）［J］，2011，36（1）:7-12.

［10］Zhu Y，Zeng W，Zhang F，et al.Materials Science and Engineering:A［J］，2012，553:112-118.

［11］Giglio M，ManesA，ViganòF.InternationalJournalof Mechanical Sciences［J］，2012，54（1）:121-135.

［12］Li Yanmei（李艳梅），Zhou Hai（周 海）.Manufacturing Technology and Machine Tools（制造技术与机床）［J］，2012（4）:104-107.

［13］Chen Rongping（陈荣平），Huang Rui（黄锐），Wang Yongchao（王勇超），et al.Aeronautical Manufacturing Technology（航空制造技术）［J］，2013（16）:100-102.

［14］Zhu S，Yang H，Guo L G，et al.Computational Materials Science［J］，2012，65:221-229.

［15］Wong C C，Dean T A，Lin J.International Journal of Machine Tools and Manufacture［J］，2003，43（14）:1 419-1 435.

［16］Shi Feng（石 丰）.Dissertation for Master（硕士论文）［D］.Xi'an:Northwestern Polytechnical University，2014.

［17］Li Lijing（李利境）.Dissertation for Master（硕士论文）［D］.Xi'an:Northwestern Polytechnical University，2015.

［18］Chu Qiang（褚 强）.Dissertation for Master（硕士论文）［D］.Xi'an:Northwestern Polytechnical University，2015.

［19］Semiatin S L，Montheillet F，Shen G，et al.Metallurgical and Materials Transactions A［J］，2002，33（8）:2 719-2 727.

［20］Semiatin S L，Knisley S L，Fagin P N，et al.Metallurgical and Materials Transactions A［J］，2003，34（10）:2 377-2 386.

［21］Jenkouk V，Hirt G，Franzke M，et al.CIRP Annals-Manufacturing Technology［J］，2012，61（1）:267-270.

［22］Zhou G，Hua L，Qian D，et al.International Journal of Mechanical Sciences［J］，2012，59（1）:1-7.

［23］Qian D，Pan Y.Computational Materials Science［J］，2013，70:24-36.

［24］Sun Z，Guo S，Yang H.Acta Materialia［J］，2013，61（6）:2 057-2 064.

［25］Wu C，Yang H.Journal of Materials Processing Technology［J］，2013，213（11）:2 033-2 041.

［26］Semiatin S L，Kinsel K T，Pilchak A L，et al.Metallurgical and Materials Transactions A［J］，2013，44（8）:3 852-3 865.

［27］Li H，Fu M W，Lu J，et al.International Journal of Plasticity ［J］，2011，27（2）:147-180.

［28］He J，Cui Z，Chen F，et al.Materials&Design［J］，2013，52:547-555.

（编辑 盖少飞）

Advances in Rolling-Spinning Technique of Titanium Tubes

GUO Jing，ZHAN Mei，YANG He
（State Key Laboratory of Solidification Processing，School of Materials Science and Engineering，Northwestern Polytechnical University，Xi’an 710072，China）

Abstract:Due to the characteristics of light weight，high strength and good corrosion resistance，titanium tubes have been widely applied and needed in the fields of aviation，aerospace and weapon.Considering that the existing processes are difficult to manufacture long，thin-walled titanium tubes with large diameter in efficiency and at low cost，a new tube forming technique by combining ring-rolling and tube spinning（called rolling-spinning）is developed.In the rolling-spinning process，blanks experience continuous local loading forming under the line contact action in ring-rolling process and point contact action in tube spinning process.These forming characteristics would lead to complex deformation history，inhomogeneous microstructure and fracture，which would finally affect the performance of tubes.Therefore，based on the twophase self-consistent model and Oyane criterion，a macro-micro finite element model coupling the damage effects is established.Using this model，the macro deformation behaviors，microstructure and damage evolutions are investigated.The results indicate that after the rolling-spinning process，the strain and α grain size are largest in the outer zone of the workpiece，while the strain and α grain size are almost same in the inner and center zones of the workpiece；the temperature and volume fraction of α phase decrease along from the outer surface to inner surface of the workpiece；the fracture would occur in the inner surface of workpiece during the spinning process due to the coupling effects of positive stress triaxiality and high strain rate.

Key words:titanium alloy；rolling-spinning；finite element method；microstructure evolution；damage evolution

中图分类号：TG306

文献标识码：A

文章编号：1674-3962（2016）04-0275-09

收稿日期：2015-12-10

基金项目：国家自然科学基金优秀青年基金（51222509）；凝固技术国家重点实验室自主课题（97-QZ-2014，90-QP-2013）

通讯作者：詹 梅，女，1972年生，教授，博士生导师，Email:zhanmei@nwpu.edu.cn

DOI:10.7502/j.issn.1674-3962.2016.04.05