对八年级数学这两个“思考”的认识
2016-07-13杨甫友
杨甫友

中图分类号:G633.6 文献标识码:B 文章编号:1672-1578(2016)06-0227-02
对人教版八年级数学上册107页,109页关于平方差公式和完全平方差公式的思考的一点看法:
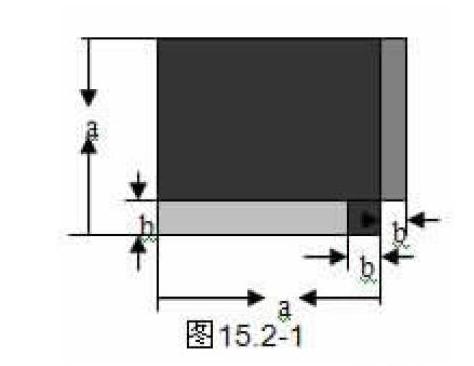
思考1 你能根据图15.2-1中的面积说明平方差公式吗?
笔者在上这节内容时,学生对这道题目不知所措,作为教师当然知道编者的意图,但作为学生根本不知道这个题目的意思,过去提到图形的面积一般都是求阴影部分的面积,如果这道题目是要我们求阴影部分的面积,那面积应该为a2-ab+b2,有的学生去求整个图形的面积为a2+ab-b2。
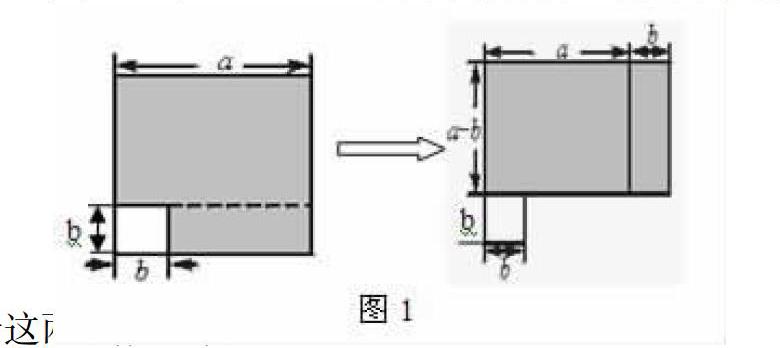
这些都不是而平方差公式左边的式子(a+b)(a-b)和右边的式子a2-b2,这两个都不是这个题目要求我们求出的图形的面积.同学们干脆说此图形不能说明平方差公式。我只有引导学生把这个图形进行折分(如图1),这样学生们一看就懂。这是什么原因呢?
题目对题设与结论根本没有说清楚,同学们刚学习平方差公式,也对这个公式的结构还不够熟悉,也就不能灵活应用在实际生活当中。不会从平方差公式的结构去考虑图形的面积,究竟要我们做什么?从图形上看要么求阴影部分的面积,要么求整个图形的面积,都不是平方差公式的表达式,說明图形也没说明白。
编者为了求新、奇、趣,为了吸引学生的注意力,为了体现新课程的理念,煞费苦心地创设迷人的问题情境,这道题目如果同学们能够正确理解,当然能够发展学生的思维能力,但对于这道题目在这里成了同学们猜答案、对答案的过程,笔者认为这道题目应该作一下修改,题目设置应简洁,也能体现课堂教学的时间、学生的思考、消化、吸收的时间,怎样学生就不会有特大的压力。这个问题的题目及图形应作修改:
如 请从这个大正方形边长为a的纸板上,剪下一个边长为b的小正方形,如图1,然后把胜余的图形拼成一个长方形,你能根据图中的面积说明平方差公式吗?
(a+b)(a-b)=a2-b2即两个数的和与这两个数的差的积,等于这两个数的平方差。
图形折分后同学们都称赞这个题目其实不难呀,为什么我们就没想到呢?这里只用到两种不同的方法求出了同一个图形的面积,根据面积相等就得到了平方差公式。
思考2 你能根据图15.2-2和15.2-3中的面积说明完全平方公式吗?
这里受到上一道题目来的影响,同学们更是茫然,想到这个图形可能也是求某一部分的面积,象上一题目不是求整体的面积;其实不然恰恰这个题目是求整个图形的面积,用整体的观念求出正方形的面积为(a+b)2,再用分割法求出各个图形的面积再求它们的和a2+2ab+b2。这样很简单就说明了完全平方和公式。此题目及图形也应该作修改:
如 你能根据图2图形中的数据,用不同的方法求出整个图形的面积说明完全平方和公式吗?
(a+b)2=a2+2ab+b2
即两数的和的平方,等于它们的平方和,加它们的积的2倍。
而图15.2-3中如果从(a-b)2出发来考虑,要求求出大正方形(阴影部分)的面积,但小正方形也是阴影出现,究竟求那一个图形的面积?根据编者的意图肯定是求大的正方形(阴影部分)的面积,要是把题目及图形改变一下,同学们就一目了然。
如 如图3根据图中的数据用不同的方法求出图中阴影部分的面积。
一种方法是直接表示阴影部分(正方形)的面积为(a-b)2;另一种是用边长为a的大正方形的面积减去一个边长为b的小正方形的面积和两个矩形的面积为a2-(a-b)b-(a-b)b-b2化简得a2-2ab+b2即得到了完全平方差公式(a-b)2 =a2-2ab+b2即两数的差的平方,等于它们的平方和,减它们的积的2倍。
这两个思考的题目及图形都没有说清楚,各个图形所求的面积有所不同(阴影部分的区分),这就给我们教师提出了更高的要求,促使教师去钻研教材,寻求切实有效的解决方法;有效激发学生数学潜能,也就是在平常的教学中,我们教师要善于思考,注重挖掘题目中潜在的价值,引导学生敢干探索、勇于探索、锐意进取的学习精神,不断提高学生的探究能力和创新能力。
"理解中学数学教材编写的意图"这件事应该是不难办的!因为这教材还一定会是具有学材功能的,而且学材这个功能是不必疑的首要功能。……教师有责任在教学生掌握知识的同时,还要让学生明白,只有进一步的学习才能更深刻的认识这一知识。另外,将学生的状况搞清楚,实行因材施教,之后的事就容易了,因为上好数学课的前提都具备了,下面就是努力教书了。
