现实生活中的数学问题

刘英婕

【摘 要】数学在生活中的应用是非常广泛的，在生活中得很多方面都存在数学的影子。如运用数学知识与方法分析生活中经济方面的问题；或者运用数理逻辑对生活中的问题做出正确的推断与选择；同时数学概率方面的知识都被人们经常运用在体育竞技方面。本文就是从人们一些日常的生活中去研究数学在生活中的运用。

【关键词】数学；经济生活；数理逻辑；体育竞技

数学作为一门自然科学在信息爆炸的今天，它的影响可谓无处不在。它不仅是人们日常生活的帮手，更是人类发展进步必不可少的一把钥匙。在日常生活中，数学作为一种思维方法，被运用在生活的许多方面，体现出数学这门学科的无穷魅力。

1 经济生活中的数学问题

经济与数学有着千丝万缕的联系。一方面经济概念、新的经济理论的出炉，往往都有着深刻的数学背景； 另一方面，作为经济学家都必须掌握相关的数学知识， 以便使这些知识应用到经济研究中， 使经济思想更深刻、更严密、更具一般性。在我们的日常生活中， 数学已不再是单纯的用作计数或统计， 还常用于对经济活动中的一些复杂现象进行分析， 如风险利润、股票债券、市场预测、投资决策、储蓄保险等等。利用数学知识与数学方法进行分析， 将有助于我们理解这些经济活动， 找出其中的规律， 并作出决策。

1.1 小本经营者的初等代数问题

经营者所追求的是利润的最大化， 而最大利润的获得通常有两个途径： 一是薄利多销， 二是提高售价。但在需求有限的情况下， 薄利并不能获得高额利润，提高售价又会减少销量， 利润也会随之下降。如某经销商将进货单价为8 元的商品按每件10 元售出时，每天可销售100 件；现在他想采用提高售价的办法来增加利润，已知这种商品每件每提价1 元， 日销量就要减少10 件。那么， 他把售价定为每件多少元， 才能使每天获利最大？每天的最大利润是多少？

设：将售价定为每件x元， 每天可获利y元， 则有：

y=（x-8）[ 100-10（x-10）] =-10（x-14）2+360

所以， 当把售出价定为每件14元时， 每天获利最大，为360元。这样， 我们用二次函数的知识巧妙的解决了最大利润问题.

1.2 股民必须具备的数学常识

据深、沪证券交易所公布， 截至2004 年12 月底， 证券市场开户数合计为7254.27 万；而2005 年1月6 日， 中国人口总数达到13 亿。可以算出， 目前证券市场投资者占中国总人口比例约为5.58%。深沪市总市值为37055.57 亿元， 占GDP 比重约为31.74%， 证券市场在国民经济中的地位越来越重要。炒股不仅需要精明的经济头脑和良好的心理素质， 更需要一定的数学知识。分析、综合、推理、计算、决策， 数学无时无刻不在显示它在股市中的作用。

我们来看一个小问题： 股民A 用1000 元人民币购买了一手股票， 随即将这手股票转卖给B，获利10%；而后B 又将这手股票返卖给A，但B 损失了10%。最后A 按B 卖给A 的价格九折将这手股票再卖给了B。

现在我们要知道A 在上述股票交易中A、B 的盈亏状况如何？ 解决此类问题的着眼点在于搞清股票交易中， 盈亏是以买入与卖出一个回合中支出与盈利情况决定的， 当收入大于支出时为盈利， 相反是亏本。本题A 在第一回合中盈利100元.B在第一回合中， 先以1000（1+10%）即1100 元买入，又以1000（1+10%）（1-10%）即990 元卖出，这样A 在第二回合中以990 元买入而以990×90%元卖出，亏损99 元，故整个交易中A 获利1 元。这是一个简单的算术问题。

1.3 购买住房问题

日常生活中处处都有数学问题的存在。只有我们留意观察，才能体会到其中的微妙。下面，就来看一个我们生活中的数学问题。现在买房的家庭日渐增多，在房屋质量相同的前提下，有些家庭认为买便宜一些的楼盘可以省钱，但是便宜的楼盘往往离市中心较远；但是有些家庭却选择楼盘较贵离市中心近的楼盘.那么，到底选择那种更为经济呢？当然，影响购房的因素很多，我们只就其中一些主要方面讨论一下。拿市中心较近的A楼盘和相对来说离市中心较远的B楼盘来进行比较，A楼盘是每平方米7100元，而B楼盘每平方米仅售2600元.有的家庭一看回龙观便宜那么多，就选择了回龙观。其实，我们不妨先计算一下，就知道这种选择到底可不可行。以下分两种情形来说明：

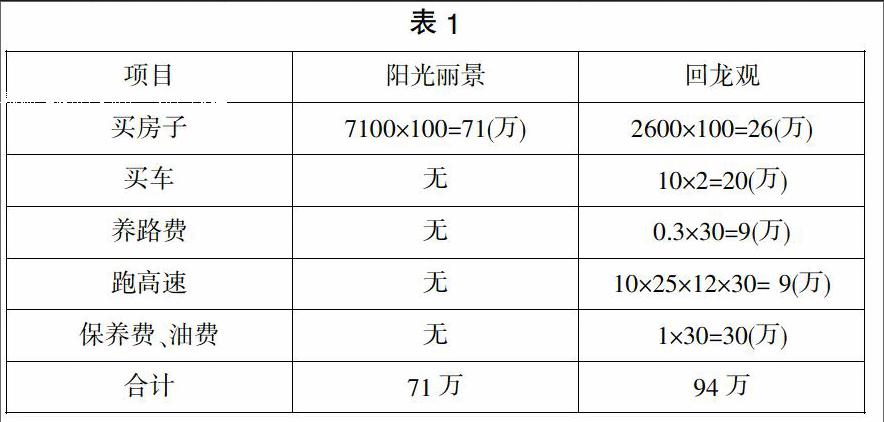
如果都买100平方米房的话，那么A楼盘就是71万，B楼盘是26万。一般来说，要住三四十年，就算三十年。因为比较远，如果还要买一辆10万元的车，三十年就买两辆（国家规定一辆车最多开十五年，十五年后则报废！） 10×2=20（万）一辆车每年还要交3000元的养路费0.3×30=9（万）。如果天天都跑高速公路的话，就算每月上班25天，每天10元钱，三十年就是10×25×12×30= 9（万）。买车的话，每年还要油费、修车、洗车等等，每年最少还要花1万元，三十年就是30万。如表1：

真是不算不知道，一算吓一跳.如果这样一算，买“阳光丽景”的房子似乎比买“回龙观”的房子要划算。

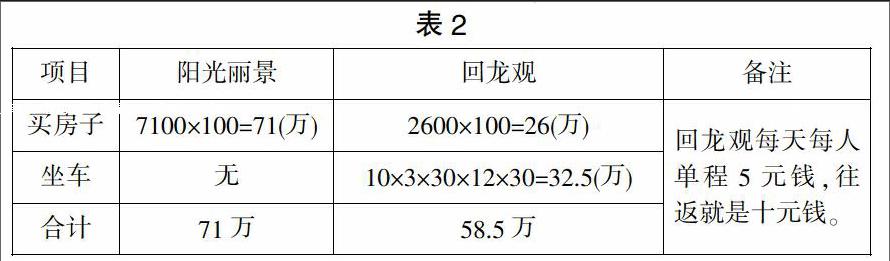
刚才算了一下如果买车的话，买哪里的房子更合算，那么如果不买车，天天坐公交车呢？让我们画一个表格进行分析吧！（假定一家三口人，每人每天10元费，一个月按30天计算）。

表2

所以说，如果不买车，每天坐公交车的话，那么买回龙观的房子就比买阳光丽景 的房子要实惠.这就是“生活中的数学”！只有我们在生活中留意观察，才能发现其中的微妙。

1.4 打折销售中的数学知识运用

“打折”的销售方式正成为一些超市扩大营业额的主要手段.进入销售旺季时， 一些商场把“九折”、“五折起”等打折广告语张贴在超市门口最显眼处， 至于具体实施办法， 有的只字不提。对于打折商品， 商家也都有明确的限制， 有些打折商品甚至存在不法商家事先抬高价格再低折出售的现象。对于低价打折的商品， 很多都是过时、过季或实用性不强的商品。更令消费者不能忍受的是， 自以为买来了低价货， 但其实并没有便宜多少.

我们来看一个具体的例子：

某商店将彩电先按原价提高40%， 然后在广告中写上“大酬宾， 八折优惠”， 结果彩电比原价多赚了270元， 那么作为消费者知不知道每台彩电原价应是多少元呢？设每台彩电原价是x 元， 依题意有下列方程：

X（1+40%）×80%=X+270

解此方程X=2250

由此可知， 每台彩电原价应是2250 元， 商家加价40%后， 变为每台3150 元， 再按8 折即每台2520元销售给消费者， （下转第266页）（上接第264页）“八折优惠”的欺骗性被揭穿。

2 数理逻辑在排队论中的应用

排队论， 又称随机服务系统理论， 它是研究服务系统中排队现象随机规律的学科，广泛应用于计算机网络、生产、运输、库存等随机服务系统。将数理逻辑的理论应用于排队论中，可以解决生产实践中的很多相关问题。

排队论主要应用数理逻辑中的范式理论，范式包括合取范式和析取范式，通过判断范式的真值情况，来判断排队的情况。

例如， 甲、乙、丙、丁四个人出去参加比赛回来后，向外部透露比赛结果。甲说：丙第一，乙第二；乙说：丙第二，丁第三；丙说：甲第二， 丁第四。已知这三个人说的都是一句真，一句假，并且无并列情况，则四个人的实际名次如何？

解析：用C1 表示丙第一；用B2 表示乙第二； 用C2 表示丙第二； 用D3 表示丁第三； 用A2 表示甲第二；用D4 表示丁第四；则因为每个人的话中至少有一个真命题，所以它们的析取为真命题，进而，这三个真命题的合取也是真命题，D4是一个真命题，同时这又是一个合取范式，现将其转化为析取范式。

T=（C1∪B2）∩（C2∪D3）∩（A2∪D4）

=（C1∩C2∩A2）∪（C1∩C2∩D4）∪（C1∩D3∩A2）∪（C1∪D3∩D4） ∪（B2∩C2∩A2）∪

（B2∩C2∩D4）∪（B2∩D3∩A2）∪（B2∩D3∩D4）

=m1∪m2∪m3∪m4∪m5∪m6∪m7∪m8

因为无并列情况， 所以m1、m5、m6、m7 均为假命题； 又因为一个人不可能同时占两名次， 所以m2、m4、m8 也是假命题， 而该公式又是一个真命题，所以m3=C1∩D3∩A2 就一定是一个真命题，即丙第一，丁第三， 甲第二，这样乙就只能是第四了，于是得出实际上的比赛名次如下： 丙第一， 甲第二， 丁第三，乙第四。

再如 从甲、乙、丙、丁4 个人之中派两个出去执行任务，按下列3 个条件共有几种派法如何派？（1）如果派甲去，那么丙和丁之中至少要派一；（2）乙和丙不能同时都去；（3）如果派丙去，那么丁必须留下。

因为必须派两个人去， 所以m1、m2 和m4 均为假命题， 于是由m3、m5、m6、m7 为真命题，共有下列3 种方案：

（1） A、C 不去， B、D 去；

（2） A、C 去， B、D 不去；

（3） A、D 去， B、C 不去。

以上我们给出了一个用于解决排队论问题的比较系统的方法。

数学在人们实际生活中的运用远远不止上面那几方面，而且数学在人类历史的发展中将充当越来越重要的角色。不管你是社会中的职业是什么，都离不开数学这包神奇的钥匙。只要你掌握好这包钥匙，你的生活也将由难变易，生活也将多姿多彩。

[责任编辑：杨玉洁]