随机激励的非线性Markov跳变系统的稳态响应*

宦荣华马云双郝琪朱位秋

（1.浙江大学应用力学研究所，杭州 310027）（2.中国南车青岛四方机车车辆股份有限公司，青岛 266111）



随机激励的非线性Markov跳变系统的稳态响应*

宦荣华1†马云双2郝琪1朱位秋1

（1.浙江大学应用力学研究所，杭州 310027）（2.中国南车青岛四方机车车辆股份有限公司，青岛 266111）

摘要大量实际工程问题需要用同时包含连续和离散变量的Markov跳变系统来描述.本文介绍了一类随机激励的单自由度（强）非线性Markov跳变系统的稳态响应的研究方法.首先，基于随机平均法导出具有Markov跳变参数的平均Itô随机微分方程，原系统方程的维数得到降低.接着，根据跳变过程原理，建立Fokker-Planck-Kolmogorov（FPK）方程组，方程组中的方程与系统的结构状态一一对应且互相耦合.求解该FPK方程组，得到Markov跳变系统的稳态随机响应及其统计量.最后，以一个高斯白噪声激励的Markov跳变Duffing振子为例，计算得到不同跳变规律下系统的稳态响应.研究结果表明，Markov跳变系统的稳态响应可以看作是各结构状态子系统稳态响应的加权和，加权值由跳变规律决定.

关键词Markov跳变， 随机激励， 非线性， 随机平均法

2014-11-01收到第1稿，2015-04-01收到修改稿.

*国家自然科学基金资助项目（11372271，11432012，51175474）、“973”计划（2011CB711105）

引言

随着计算机、军事、生物和工业技术的发展，经典的单结构系统理论已不能满足实际应用的需要，而一类既能反映系统状态变化又能反映系统结构变化的系统，即Markov跳变系统，从20世纪中叶提出以来引起人们的很大关注. Markov跳变系统是一个同时包含连续和离散变量的混合系统，离散跳变随机过程的引入，使得系统的动力学行为更为复杂，也增加了系统动力学研究的难度.因此，Markov跳变系统动力学的研究具有重要科学意义.

Markov跳变系统最初由Krasivskii和Lidskii提出［1］，经过几十年的发展，已经取得了一些成果［2 -3］. Markov跳变系统的稳定性理论是由Kats 和Krasovskii最先提出的［4］.随后，M. martion［5］利用随机Lyapunov方法分析了随机噪声环境下线性Markov跳变系统的均方稳定性. Fen和Fang［6，7］将传统的Lyapunov稳定性理论拓展到随机Markov跳变系统中，提出了随机Lyapunov第二方法稳定性定理. Krasovskii等首先研究了Markov跳变系统的LQR问题. Sworder等［8］基于极大值原理研究了有限时间区间内的线性Markov跳跃系统的最优控制问题. Ghosh等［9］提出了Markov跳变系统控制问题的动态规划方法.方洋旺［3］等对近20年里面随机跳变系统在状态估计、稳定性研究以及最优控制方面的主要理论进行了总结.然而，之前的研究多为线性系统，研究内容多局限于随机稳定性与控制方面，对非线性Markov跳变系统的动力学研究还极少涉及.

本文主要研究了随机激励下非线性Markvo跳变系统的稳态响应.基于随机平均法［10 -13］对系统进行简化，导出了Markov跳变系统的平均Itô随机微分方程.建立并求解相应的FPK方程组，得到Markov跳变系统稳态振幅响应的概率分布，研究了跳变规律对系统稳态响应的影响规律.将理论结果与数值仿真结果进行对比，验证了本文理论方法的准确性.

1 平均方程

考虑一类随机激励的单自由度（强）非线性Markov跳变系统：

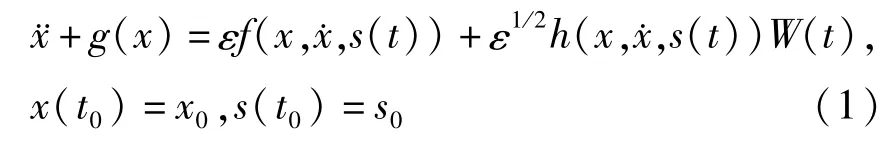
式中ε为小量，g为非线性刚度；εf为带有跳变参数的小阻尼；ε1/2hW（t）代表带有跳变参数的弱外或参数激励；W（t）为强度为2D的高斯白噪声.当s （t）固定时，函数f（x，˙x，s（t））和h（x，˙x，s（t））为x的光滑函数. s（t）是一个在有限集合S =｛1，2，…，l｝内取值的连续时间离散状态的Markov过程，s（t）代表系统结构的状态标号，l是系统所拥有的结构状态的数目.在小时间间隔Δt内，该Markov过程的转移概率为

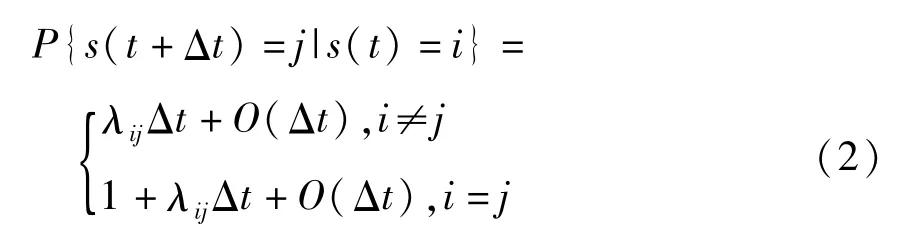
考虑独立跳变情形，即跳变过程与系统状态无关.假设系统始终运行在第i个结构状态中，无跳变发生.在此情形下，简单起见，令f（x，s（t））和h（x，s（t））简写为f（i）（x，˙x）和h（i）（x˙）.无跳变系统具有如下形式的解［10］

式中

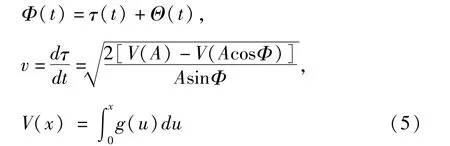
其中A，Φ，τ和υ为随机过程.运用随机平均法［10 -12］，得到关于振幅响应A的平均Itô随机微分方程

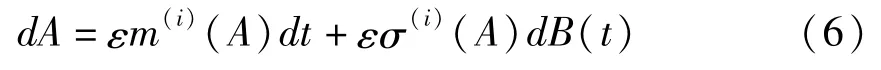
式中B（t）为单位维纳过程，扩散和漂移系数为

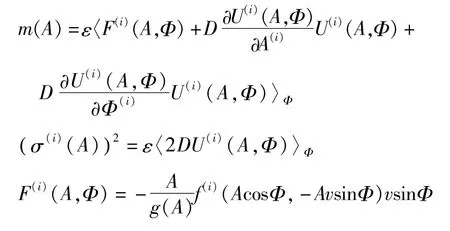
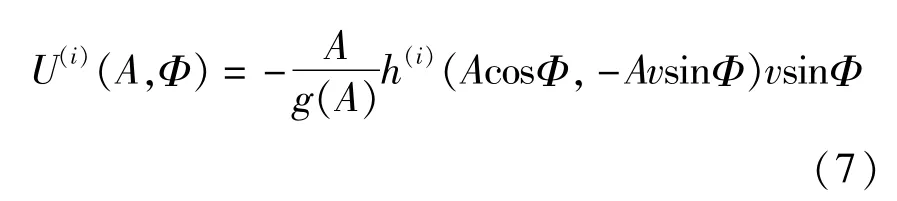
原跳变系统具有l个如式（6）所示的平均方程，平均后的跳变系统在这l个平均方程间跳变.因此，得到如下跳变系统的平均方程

式中m（A，s）和σ（A，s）为带有Markov跳变参数的扩散和漂移系数，当系统运行在第i个结构状态时，其扩散和漂移系数，即m（A，s = i）和σ（A，s = i）由方程（7）确定.

2 FPK方程

假设在很小的时间区间Δt内系统未发生跳变，则转移概率密度函数p（A，s，t｜A′，s，t′）满足如下FPK方程：

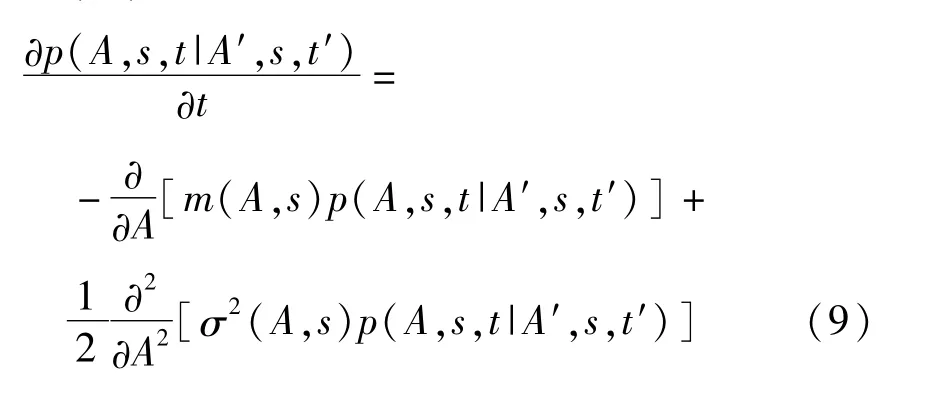
当在Δt内，系统发生了跳变，则此时概率密度函数p（A，s，t +Δt）为

式中条件概率密度q（A，s，t +Δt｜A′，r，t）表示t时刻和r状态的振幅响应A′为已知的条件下，振幅A 在t +Δt时刻和s状态的概率分布. q（A，s，t +Δt｜A′，r，t）的具体形式由实际问题的物理意义所决定.当跳变参数与系统状态无关时，即为独立跳变时，q（A，s，t +Δt｜A′，r，t）具有如下形式

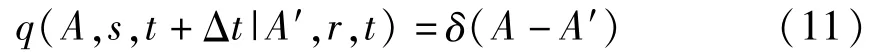
将方程（2）和（9）代入方程（10），并令Δt→0，方程（10）变为

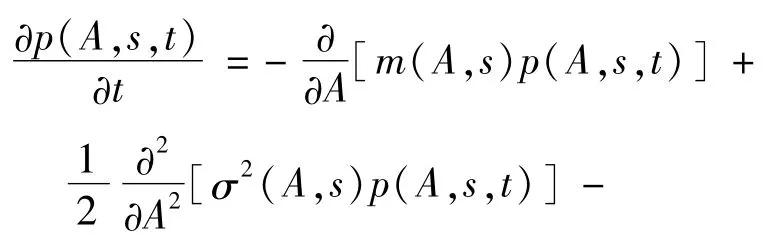
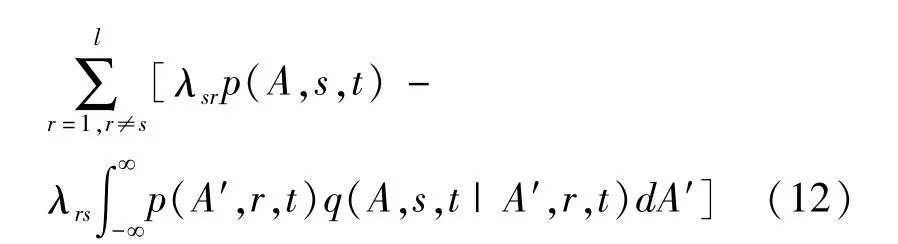
方程（12）即为混合随机过程［A，s］T联合概率密度p（A，s，t）所满足的FPK方程.对于独立跳变过程，利用式（11），FPK方程（12）可以简化为

初始条件

边界条件

式（13）是由l个方程组成的方程组（l为系统所包含的所有结构状态数目），且这些方程通过零次方项耦合. FPK方程（13）一般难以求解，即使是数值解也难以获得.若仅考虑稳态解，即令∂p/∂t =0，则方程（13）可以得到简化.通过差分法等数值方法求解简化后的FPK方程，可得到稳态联合概率密度p（A，s）.则振幅的概率密度p（A）为

式中c为归一化常数.

3 算例

考虑一个随机激励的跳变Duffing振子，其运动微分方程为

式中β（s）为跳变阻尼系数；h（s）为跳变外激励系数；W（t）为强度为2D的高斯白噪声；s为连续时间的Markov随机过程，其转移概率如式（2）所示.本文考虑2结构状态情形，即有限集合S =｛1，2｝.

利用上述随机平均法，得到如（8）式所示的平均方程，跳变扩散和漂移系数为

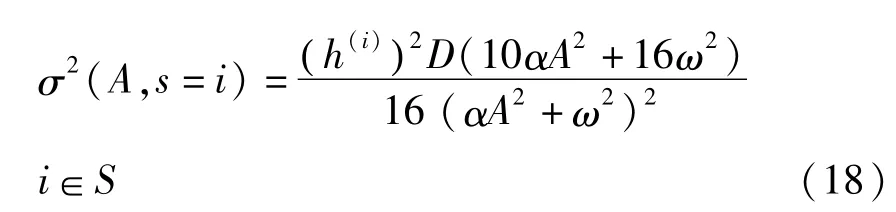
建立和求解简化后的FPK方程可得到跳变系统的振幅响应的稳态概率密度p（A）.

图1 跳变系统振幅响应的稳态概率密度Fig. 1 Stationary probabilistic density of the amplitude of jump system

图2 振幅响应的样本Fig. 2 Sample of amplitude

假设系统无量纲参数为：ω=1. 0，α=1. 0，D = 0. 1，β（s =1）=0. 1，β（s =2）=0. 2，h（s =1）=2. 0，h（s =2）=1. 0.图1为不同跳变规律下跳变系统振幅响应的稳态概率密度.图1（a）中Λ1和Λ3所代表曲线分别为系统结构状态为s =1和s =2时的无跳变系统的稳态振幅概率密度，Λ2为跳变系统的稳态振幅概率密度，结果表明，发生跳变后系统的稳态响应相比于无跳变系统发生非常大的变化，跳变对系统的响应具有很大影响.图1（a）中Λ2为对称矩阵，所对应的跳变系统为对称跳变.图1（b）为系统发生非对称跳变时的振幅稳态概率密度.当Λ =Λ4时，系统从结构状态s =1跳变到s =2的概率比跳回结构状态s =1的概率要小，即系统停留在s =1结构状态的概率较大，因此，图1（b）中Λ4代表的曲线更接近于曲线Λ1，而Λ5则更接近Λ3.显然，跳变系统的响应可以看作是各结构状态下无跳变系统响应的加权和，而加权值由跳变规律决定.不同跳变规律下系统的响应具有很大差异.图1中实线为解析结果，符号曲线代表数值仿真结果，两者吻合，表明了本文提出的理论方法的准确性.图2和3分别为振幅响应A和Markov跳变参数s（t）的一段样本.

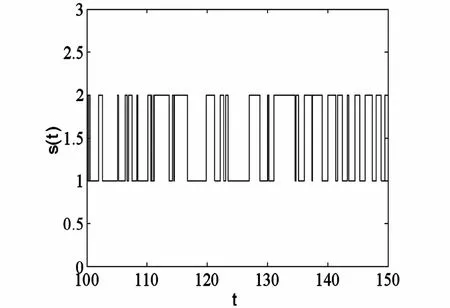
图3 Markov跳变参数s（t）的样本Fig. 3 Sample of Markov jump parameter s（t）

4 结论

本文提出了一种研究随机激励下Markov跳变非线性系统的稳态响应的求解方法.本文的主要工作是导出了非线性Markov跳变系统的平均Itô随机微分方程，得到了相应的FPK方程组.随机平均法的应用，降低了系统方程的维数，使得最后的FPK方程组的数值求解成为可能. Markov跳变Duffing振子算例的计算验证了本文提出的理论方法的有效性.

本文虽然只对单自由度Markov跳变系统的响应进行了研究，但该理论方法在多自由度Markov跳变系统的响应、稳定性与可靠性等的研究方面也具有很大潜力.

参 考 文 献

1 Krasosvkii N N，Lidskii E A. Analytical design of controllers in systems with random attributes. Automation and Remote Control，1961，22（1）：1021～1025

2 吴森堂.结构随机跳变系统理论及其应用.北京：科学出版社，2007（Wu S T. The theory of stochastic jump system and its application. Beijing：Science Press，2007（in Chinese））

3 方洋旺，伍友利，王洪强.结构随机跳变系统最优控制理论.北京：国防工业出版社，2012（Fang Y W，Wu Y L，Wang H Q. Optimal control theory of stochastic jump sytem. Beijing：National Defense Industry Press. 2012（in Chinese））

4 Kats L，Krasovskii N. On the stability of systems with random parameters. Journal of Applied Mathematics and Mechanics，1960，27（5）：809～823

5 Mariton M. Almost sure and moment stability of jump linear systems. Systems & Control Letters，1988，11（5）：393～397

6 Feng X，Loparo KA，Ji Y. et al. Stochastic stability properties of jump linear systems. IEEE Trans Automate Control，1992，37（1）：38～45

7 Fang Y G. A new general sufficient condition for almost sure stability of jump linear systems. IEEE Transaction Automate Control，1997，42（3）：378～382

8 Sworder D. Feedback control of a class of linear systems with jump parameters. IEEE Trans on Automatic Control，1969，14（1）：9～14

9 Ghosh M K，Arapostathis A，Marcus S I. Ergodic control of switching diffusions. SIAM Journal on Control and Optimization，1997，35（6）：152～198

10 Xu Z，Chung Y K. Averaging method using generalized harmonic functions for strongly nonlinear oscillators. Journal of Sound and Vibration，1994，174（4）：563～576

11 Huang Z L，Zhu W Q，Suzuki Y. Stochastic averaging of strongly nonlinear oscillators under combined harmonic and white noise excitations. Journal of Sound and Vibration，2000，238（2）：233～256

12 Huang Z L，Zhu W Q. Stochastic averaging of quasi-integrable hamiltonian systems under combined harmonic and white noise excitations. International Journal of Non-Linear Mechanics，2004，39（9）：1421～1434

13 陈林聪，朱位秋.随机扰动下简单电力系统的可靠度反馈最大化.动力学与控制学报，2010，8（1）：19～23 （Chen L C，Zhu W Q. Feedback maximization of reliability of a simple power system under random perturbations. Journal of Dynamics and Control，2010，8（1）：19～23（in Chinese））

Received 1 November 2014，revised 1 April 2015.

*This project supported by the National Natural Science Foundation of China（11372271，11432012，51175474）；“973”program（2011CB711105）

STATIONARY RESPONSE OF STOCHASTICALLY EXCITED NONLINEAR MARKOVIAN JUMP SYSTEM*

Huan Ronghua1†Ma Yunshuang2Hao Qi1Zhu Weiqiu1
（1. Zhejiang University Institute of Applied Mechanics，Hangzhou 310027，China）（2. Sifang Rolling Stock Research Institute CO. Ltd，Qingdao 266111，China）

AbstractMany practical problems should be described by nonlinear Markov jump systems involving both continuous and discrete variables. In this paper，the stationary response of stochastically excited single-degree-of-freedom（strongly）nonlinear system with Markovian jump parameters is studied. Firstly，the averaged It？differential equation with Markovian jump is derived based on the stochastic averaging method. Then，according to the Markovian jump principle，the finite set of（Fokker-Planck-Kolmogorov）FPK equations are formulated. The FPK equations coupled with each other through the absorptive terms and reductive terms. The stationary response and its statistics of the Markovian jump system can be obtained by solving the FPK equations numerically. Finally，as an example，the responses of a Markovian jump Duffing oscillator subjected to Gaussian white noise are studied. Numerical results show that the stationary response of the jump system can be regard as a weighted sum of the responses of no-jump system，and the weighted value is determined by the jump rules.

Key wordsMarkov jump， stochastic excitations， nonlinearity， stochastic averaging method

DOI：10. 6052/1672-6553-2015-035

通讯作者†E-mail：rhhuan@ zju. edu. cn

Corresponding author†E-mail：rhhuan@ zju. edu. cn