基于整体-局部高阶剪切理论的层合板多体系统的动静力学分析*

田立智刘锦阳

（上海交通大学，上海 200240）



基于整体-局部高阶剪切理论的层合板多体系统的动静力学分析*

田立智1†刘锦阳2

（上海交通大学，上海 200240）

摘要基于高阶剪切理论，推导了整体-局部1，2-3高阶位移模式.在满足层间位移连续，层间剪应力连续，以及上下表面自由的条件下，层合板每个节点的独立变量变为13，并且不随层合板层数的增加而变化.在此基础上将整体-局部1，2-3高阶位移模式推广到刚-柔耦合层合板多体系统，利用混合坐标法，基于虚功原理，建立了考虑层合板层间应力连续的多体系统动力学方程.通过静力学算例，验证了整体-局部1，2-3高阶位移模式的准确性，得到了层合板层间应力沿着厚度的分布情况.通过多体系统动力学算例，对比了传统方法的计算结果，揭示了本文方法与传统方法在计算层合板多体系统中层间应力的差异，说明了刚-柔耦合层合板多体系统考虑层间剪应力连续的必要性.

关键词整体-局部高阶剪切位移模式， 层间剪应力连续， 层合板多体系统， 应力分析

2014-10-29收到第1稿，2014-12-17收到修改稿.

*国家自然科学基金资助项目（11272203，11132007）

引言

在航空、汽车、机械等工业领域，很多运动机构为复合材料层合板结构多体系统，例如直升机机翼和风电机叶片等.通常情况下，层合板多体系统的刚-柔耦合动力学分析仅限于层合板表面的响应和应变分析，没有深入到多体系统层合板的层间应力，而层合结构特有的层间破坏问题要求准确计算层间应力，对于多体系统中的层合板结构，同样有必要进行层间应力的研究.

复合材料层合板的理论［1-2］主要包括：基于Kirchhoff假设的经典层合板理论CLT，基于Mindlin假设的一阶剪切理论FSDT，高阶剪切理论，分层理论以及Zigzag等理论.由于复合材料的各向异性和呈层性等特点，较厚层合板间的剪切和拉压应力对于结构的刚度和强度的影响较大，采用CLT和FSDT理论得到的结果很难满足精度要求.高阶剪切理论［3］可以较好地研究层合板的动力学响应，例如张伟等［4］基于高阶剪切理论研究了厚板振动的解析解，但是在层间应力的描述上仍存不足. Layerwise理论［5］可以较好计算层间应力，但是节点的独立变量随复合材料层数的增加而增加，对于层数较多的层合板，严重影响了计算效率并且增加了理论的复杂性. Zigzag理论［6］可以很好地计算层合板响应和层间应力，但对于较厚的板，需要借助平衡方程来计算横向剪切应力以提高精度.

1997年，X. Li等［7］针对正交铺设层合板提出了整体-局部高阶剪切理论.该理论在Reddy型高阶剪切理论的基本位移模式中增添了截取三次的局部位移，可以很好地计算层间应力. Zhen Wu等［8］将这种位移模式推广到了角铺设层合板结构.这种位移模式满足层间位移连续，剪应力连续和上下表面自由条件，每个节点的独立变量为13，并且不随层合板的层数而变化.

对于刚-柔耦合层合板，前人主要应用基于Mindlin假设的一阶剪切理论FSDT［9］，在此基础上侧重考虑薄板的几何非线性效应.潘科琪等［10］采用Mindlin假设计算了多体系统层合板的表面应变.但是对于较厚的层合板，非线性效应变弱，层合板层间的剪切应力连续条件需要给予考虑.

本文将基于整体-局部高阶剪切理论，针对上下表面面外剪应力为零的复合材料层合板刚-柔耦合多体系统层间应力进行研究.首先综合前人研究的整体-局部位移模式，验证了该位移模式能准确计算沿厚度方向的层间位移和应力分布，得到了层间应力沿着厚度的变化趋势，然后将整体-局部位移模式推广到复合材料层合板多体系统.通过刚柔耦合动力学算例，将应用整体-局部位移模式的刚-柔耦合层合板计算结果与传统方法的计算结果进行对比，得到刚-柔耦合层合板的层间应力变化趋势，可以看出考虑了层间剪应力连续的整体-局部位移模式与不考虑剪应力连续的理论在计算层间应力的差异，说明了在刚-柔耦合层合板多体系统中考虑层间剪应力连续的必要性.

1 整体—局部高阶剪切位移模式

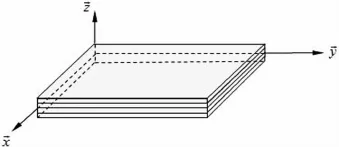
图1 层合板坐标系Fig. 1 Coordinate system of composite laminated plate

Reddy型高阶剪切理论的基本位移模式为：

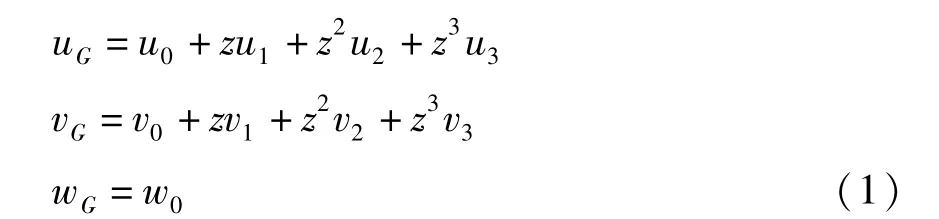
其中，vu0，u1，u2，u3为描述节点沿方向位移的独立变量，v0，v1，v2，v3为描述节点沿方向位移的独立变量，w0为描述节点沿→■z方向位移的独立变量，uG，vG，wG为对应非中面上整体坐标为z的节点的位移，后文以HSDT来简称这种位移模式.

这种位移模式考虑了剪切应力，但没有考虑层间剪应力连续和上下表面自由条件，因此不能准确计算出层间应力.整体-局部位移模式在Reddy型高阶剪切理论的基本位移模式HSDT基础上增加了局部位移，位移模式由两部分构成：

其中，uG，vG，wG为式（1）中的基本位移模式，这里称为整体位移；添加的变量ukL，vkL各层均不相同，称为局部位移.与整体位移类似，局部位移可以写为：

其中，ξk为层合板两层之间沿方向的局部坐标，可以写为：

akz - bk，其中，，k = 1， 2. . . n -1

为了减少独立变量，文献［6］与［7］将局部位移（4）分为两组应用位移连续条件，即双位移连续件：

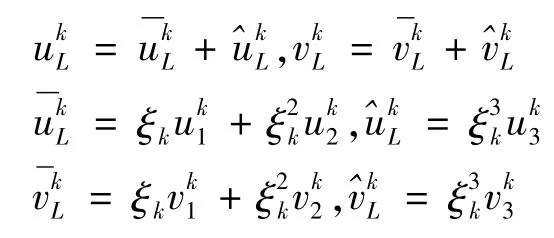
在整体-局部1，2-3位移模式下，对于n层的层合板，共有6n + 9自由度，利用层间位移连续条件可以消去4（n -1）自由度，利用层间剪应力连续可以消去2（n -1）自由度，那么剩下15自由度，最后利用上下表面自由条件，最终的自由度数目变为13.

1. 1 层间位移连续条件

应用双位移连续条件：

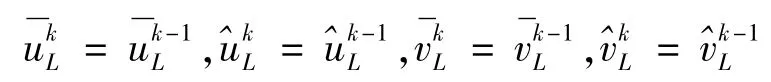
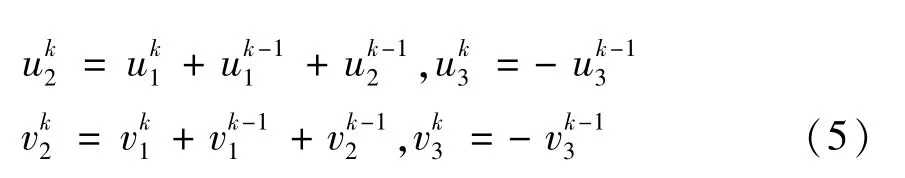
其中，k = 1，2，3，…n -1.

1. 2 层间剪力连续条件

应用层间剪切应力连续条件：

其中：

Q44k，Q45k，Q55k为第k层转换后的刚度系数，它们的具体表达式见参考文献［11］为剪切应变，可表示为：

将式（5）代入（4）、（6）、（7）以及层间剪应力连续条件，可以得到，，与，的递推关系：

其中：

1. 3 下表面自由条件

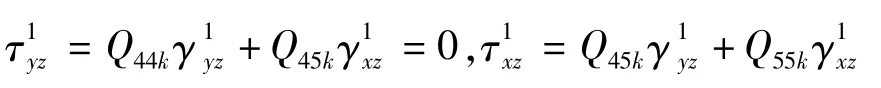
将式（2）、（4）、（7）代入上式可以得到：

结合式（8）的递推关系，可以假设局部位移变量为：

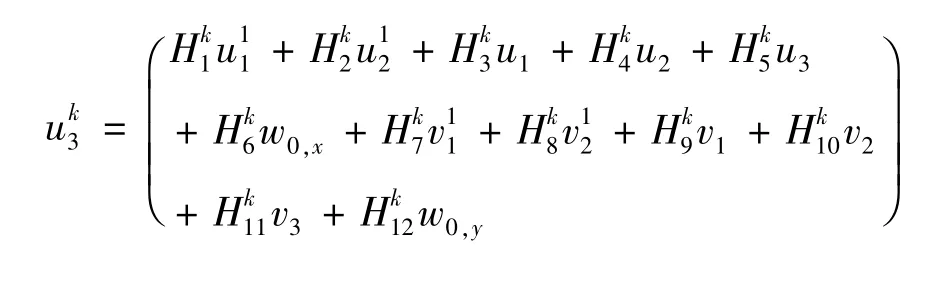
将上述表达式（10）代入式（8）可以得到：

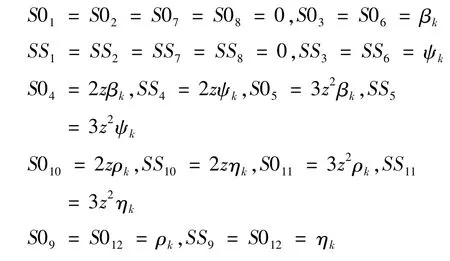
1. 4 上表面自由条件

同理，应用上表面剪应力为0的条件：

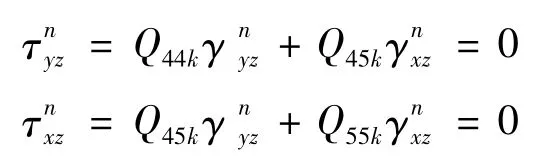
得到：

将式（10）代入上述两式，可求出u12和v12：

其中，系数A1，B1，C1，D1，E1，F1，G1，H1，J1，K1，A2，B2，C2，D2，E2，F2，G2，H2，J2，K2可以用Fni，表示.将式（12）代入式（10），并代入整体位移模式，最终可以得到：

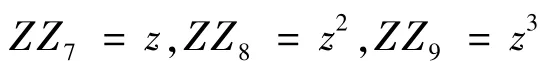
2 刚柔耦合板的动力学描述

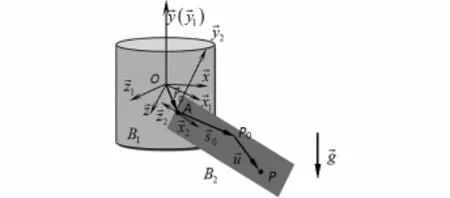
图2 刚-柔耦合复合材料层合板Fig. 2 Rigid-flexible coupling composite laminated plate

如图2所示，刚-柔动力学系统由作旋转运动的中心刚体B1和复合材料层合板B2组成. B2与在点A处相固接.建立惯性坐标系， B1的连体基■和B2的浮动坐标系■

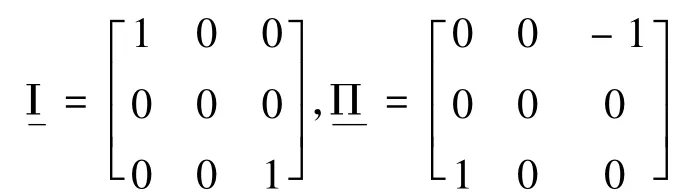
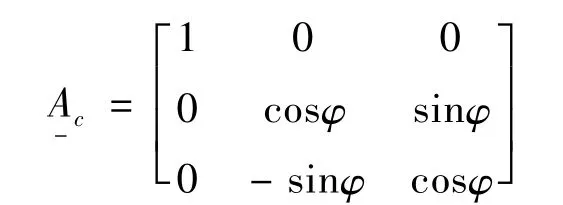
那么可以得到：

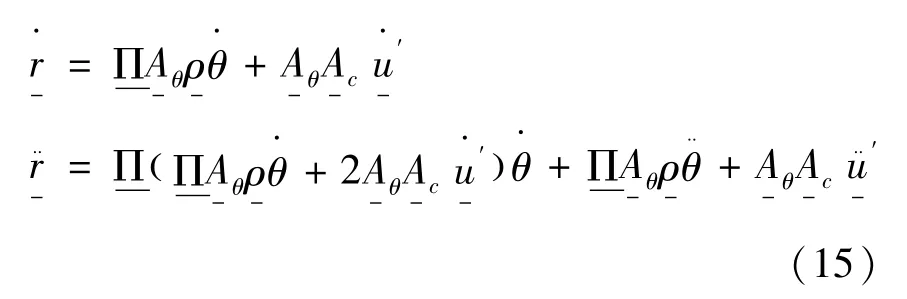
3 整体局部位移模式的层合板有限元离散

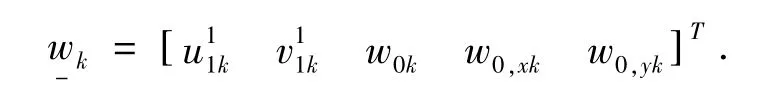
对面内变量采取双线性插值；对w0基于薄板非协调单元进行插值，即：

将式（16）代入式（13），可以得到：

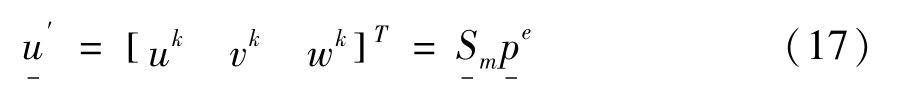
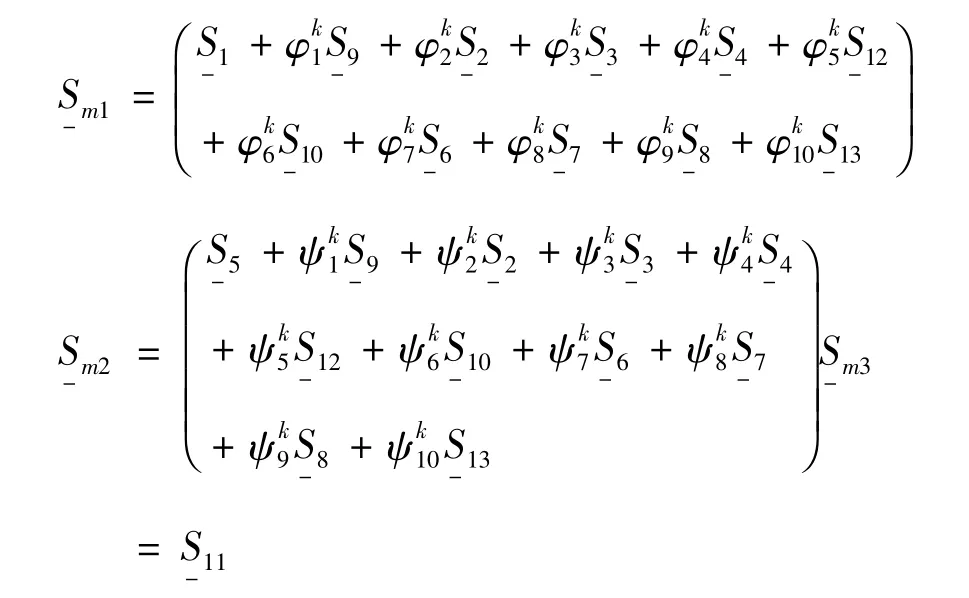
而文献［10］所采用的FSDT理论的离散为：

其中：

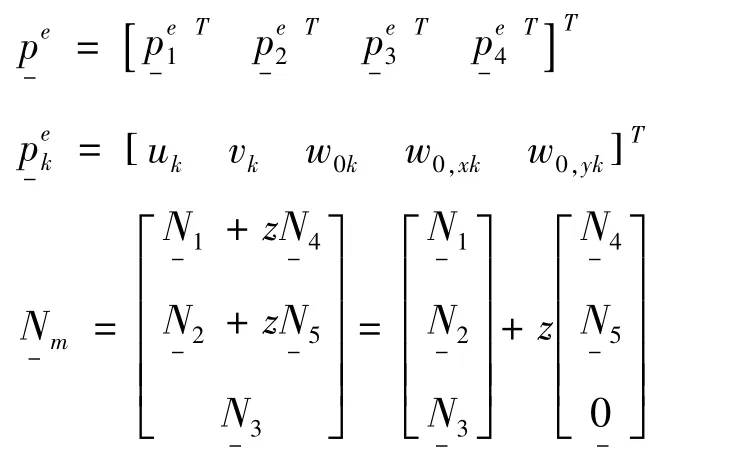
设J0为中心刚体的转动惯量，为层合板的广义坐标阵，为活动坐标，令：

应变可表示为：

将式（17）和式（18）代入式（19）可以得到：

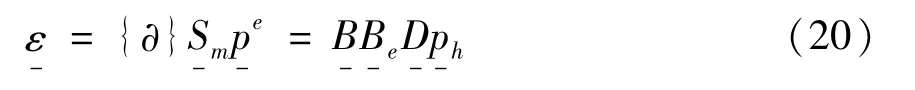
将式（17）代入式（15）可以得到：

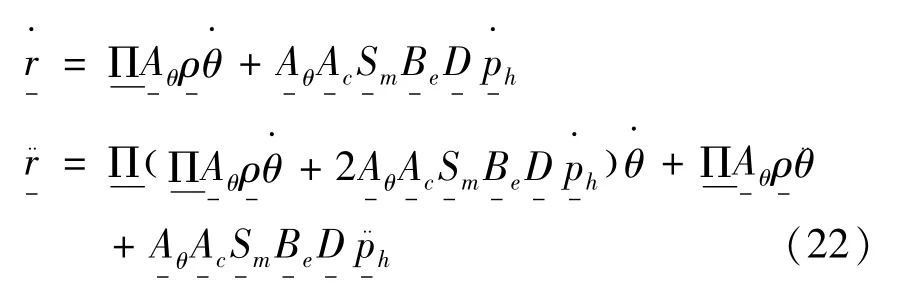
设J0为中心刚体关于→■y轴的转动惯量，那么惯性力的虚功率为：

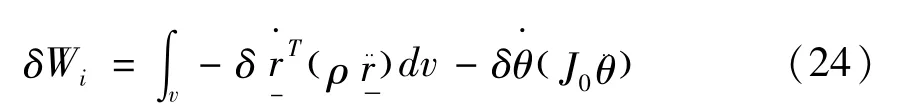
将式（23）代入式（24）可以得到：

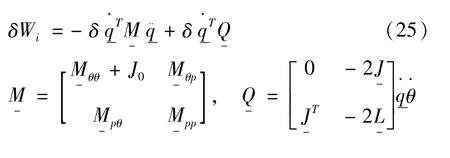
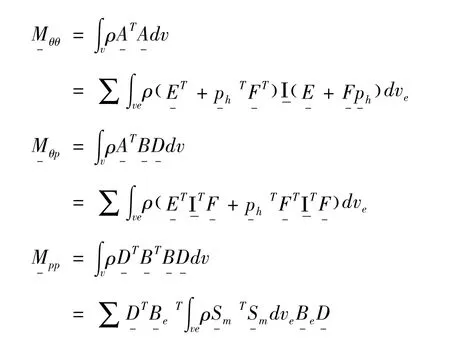
设重力加速度在惯性基下的坐标阵为g-f，重力的虚功率为：

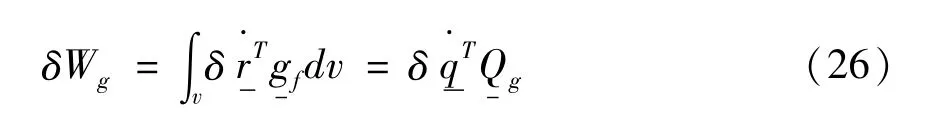
根据虚功原理，有如下关系：

将式（21）、（25）、（26）代入上式可以得到：

可以得到系统的动力学方程为：

4 整体-局部位移模式的验证

图3 两边简支复合材料层合板Fig. 3 Composite laminated plate with simply supported edges

单位体积分布载荷在总体坐标系下的坐标列阵为f-，上下表面的单位面积的分布载荷在总体坐标系下的坐标列阵分布为和.广义力阵为：

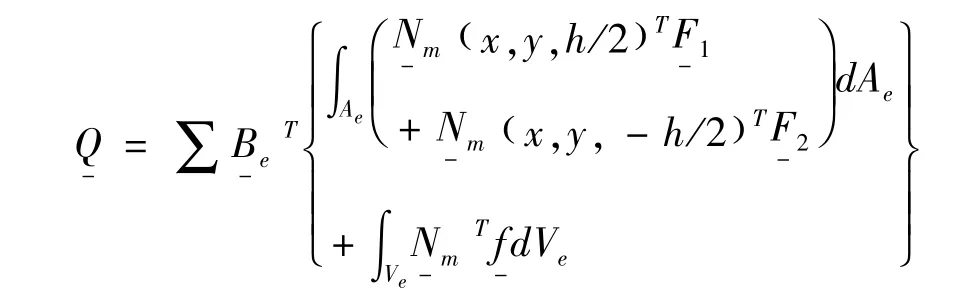
G23= 0. 2×106Pa，v12= v13= v23= 0. 25

E1= 2. 5×107Pa，E2= 106Pa，G12= G13= 0. 5×106Pa，，长厚比L/ h = 4，所有变量均无量纲化.

图4 两边简支面内位移u沿厚度的变化Fig.4 Relationship of in - plane displacement u and the thickness Z

图5 两边简支面内正应力σx沿厚度的变化Fig. 5 Relationship of in - plane normal stress σxand and the thickness Z

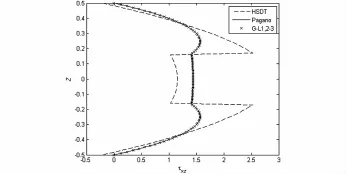
图6 两边简支面外剪切应力τxz沿厚度的变化Fig.6 Relationship of out -plane shear stress τxzand the thickness Z

图4～图6为两边简支条件下位移与应力沿厚度方向的变化.图4为分别利用Reddy型高阶剪切理论基本位移模式（HSDT），Pagano解析解以及本文整体-局部1，2-3位移模式（G-L1，2-3）得到的点（0，0）处位移u与厚度的关系，整体局部1，2-3与解析解吻合得很好，而高阶剪切理论在分层处开始出现误差，不能很好地反映出层间的位移变化；图5为分别利用三种方法求得的点（L/2，0）处正应力σx与厚度的关系，整体局部1，2-3位移模式可以很好地反映出面内应力的变化，而HSDT平滑变化，仅大致描述了应力变化的平均值；图6为面外剪切应力τxz与厚度的关系，HSDT与解析解差异很大，且不满足上下表面剪力为0的条件，而GL1，2-3与解析解吻合很好.不难看出来，整体局部1，2-3位移模式可以精确地计算出分处出现的层间剪应力，很好地反映出层间应力沿着厚度的变化，精度明显高于传统的高阶剪切论.

5 整体-局部位移模式的刚柔耦合板研究

如图2所示的复合材料板刚柔耦合动力学模型.

r=[ x y z ]T，

0000

其中，

x0= 0. 1m ，y0= z0= 0，J0= 1 Kg. m2

层合板的参数为：长L = 0. 8m，宽H = 0. 1m，厚h =0. 01m，铺层角（0/90/0），材料常数为：

令倾斜角φ为45o，由于层合板的大变形效应，中心刚体会转动.取时间历程2s时，计算t = 0. 1s时层合板应力沿着厚度的变化.研究如图2所示刚-柔耦合系统中浮动坐标系(A)下的四个节点：B（L/2，0），C（L/2，- H/2），D（L，0），E（L，- H/2）.计算四个节点的应力沿着厚度的变化.

图7 中心刚体角速度与时间变化Fig. 7 Angular velocity - time relationships of the central rigid body

图8 点B面外剪切应力τxz沿厚度变化Fig. 8 Relationship of out-plane shear stress τxzand the thickness Z at Point B

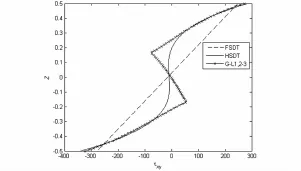
图9 点C面内正应力τxy沿厚度变化Fig. 9 Relationship of in-plane normal stress τxyand the thickness Z at Point

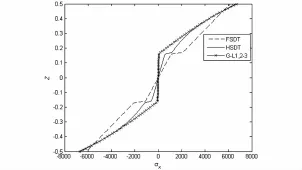
图10 点D面内正应力σx沿厚度变化Fig. 10 Relationship of in-plane normal stress σxand and the thickness Z at Point D

图7为分别利用文献［10］的一阶剪切理论FSDT，高阶剪切理论HSDT，以及本文的整体-局部1，2-3理论G-L1，2-3计算出来的中心刚体的转动角速度.图8到图14为分别利用一阶剪切理论，高阶剪切理论，以及整体-局部1，2-3理论，计算的多体系统刚柔耦合系统中，绕着中心刚体转动的层合板在t =0. 1s时各点的应力沿着厚度的变化.

图11 点D面内正应力σy沿厚度变化Fig. 11 Relationship of in-plane normal stress σyand the thickness Z at Point D

图12 点D面外剪切应力τxz沿厚度变化Fig. 12 Relationship of out-plane shear stress τxzand the thickness Z at Point D

图13 点E面内正应力σx沿厚度变化Fig. 13 Relationship of in-plane normal stress σxand the thickness Z at Point E

图7为分别利用三种模型计算出来的中心刚体的角速度时间历程，三种模型在计算中心刚体的角速度相同，说明了层合板模型对于刚体的影响可以忽略.图8为点B的τxz沿厚度变化，可以看出，一阶剪切理论与高阶剪切理论所得到的应力沿厚度呈不规则变化，而本文模型反映出应力在层间出现的变化与静力学中的面外剪切应力的变化趋势大致符合；图9为点C的τxy沿着厚度的变化，一阶理论的应力值呈线性变化，高阶剪切理论仅描述了平均值，而本文模型的应力结果可以较好地反映出层间变化.图10与图11分别为点D的σx与σy沿厚度的变化，图中显示，一阶剪切理论差异较为明显，在分层处，一阶理论和高阶理论均有明显的突变，而本文模型与静力学中面内正应力的变化趋势相符.图12为点D处的τxz沿厚度变化，图中显示，一阶剪切理论和高阶剪切理论差异均较大，本文基于整体-局部高阶剪切理论的动力学模型满足上下表面自由条件，可以较好地反映出层间应力的变化.图13为点E的σx沿厚度的变化.图14为点E处的τxy沿厚度的变化，其变化规律与点C相同.由于一阶剪切和高阶剪切没有考虑层间应力连续，对于层合板，几种方法计算出来的应力在分层处差异最大.由此可见，本文模型可以很好地反映出刚柔耦合多体系统中层合板的层间应力的变化.

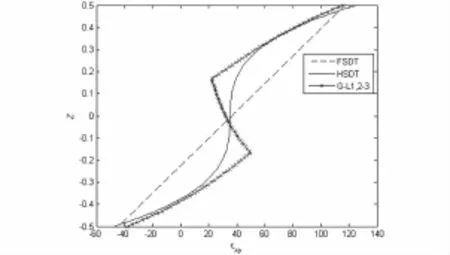
图14 点E面内剪切应力τxy沿厚度变化Fig. 14 Relationship of in-plane shear stress τxyand the thickness Z at Point E

图15 点B面外剪切应力τxz变化Fig. 15 Time history of out-plane shear stress τxzat Point B

通过图7到图14可以看出来，一阶剪切理论在计算层间应力会出现很大误差.高阶剪切理论和本文的整体-局部高阶剪切理论在分层处应力开始出现区别.考虑了层合板层间剪切应力连续的刚柔耦合层合板可以更合理的反映出具有转动效应的层合板的层间应力的变化.为了更好地对比三种模型计算出来的应力区别.现在选取层合板上述四个位置的对应中面上的四个点，计算时间历程.

图16 点C面外剪切应力τyz变化Fig. 16 Time history of out-plane shear stress τyzat Point C

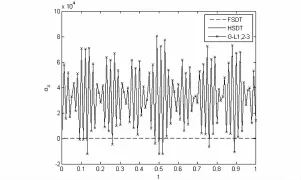
图17 点D面内正应力σx变化Fig. 17 Time history of in-plane normal stress σxat Point D

图18 点C面内位移u变化Fig. 18 Time history of in-plane displacement u at Point C

图15为位置B对应的点的面外剪切应力τxz的时间历程；图16为位置C对应的点的面外剪切应力τyz的时间历程；图17为位置D对应的点的面内正应力σx的时间历程；图18为位置C对应的点的面内位移u的时间历程；图19为位置E对应的点的面内位移v的时间历程.可以看出来不考虑层间剪切应力连续的一阶剪切理论、高阶剪切理论计算出来的应力与考虑了层间剪切应力连续的整体-局部高阶剪切理论的计算结果差异较大.而三种方法在计算响应的时候差异较小.由此可以看出来针对计算层间应力的精度问题而考虑层间剪切应力连续条件的必要性.

图19 点E面内位移v变化Fig. 19 Time history of in-plane displacement v at Point E

6 结论

（1）创新性地将整体局部高阶剪切理论扩展到刚-柔耦合多体系统，可以反映出刚柔耦合层合板层间应力沿着厚度的层间变化.

（2）在层合板刚-柔耦合多体系统中，层合板模型对于中心刚体的角速度影响较小.

（3）层合板多体系统的层间应力在分层处会出现较明显的变化，考虑了层间应力连续的模型，计算出来的层间应力的变化与静力学基本相符，但是由于惯性力的存在，面外应力在层间的变化与静力学的变化趋势存在差异，在层合板多体系统中需要考虑层间剪应力连续.

参 考 文 献

1 Zhanga Y X，Yang C H. Recent developments in finite element analysis for laminated composite plates. Composite Structures，2009，88（1）：147～157

2 Carrera E，Brischtto S. A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates. Applied Mechanics Review，2009，62（1）：1～17

3 Fiedler L，Lacarbonara W，Vestroni F. A generalized higher-order theory for buckling of thick multi-layered composite plates with normal and transverse shear strains. Composite Structures，2010，92（12）：3011～3019

4 陈丽华，孙玥，张伟.三阶剪切变形板的振东特性研究.动力学与控制学报，2014，12（1）：50～55（Chen L H，Sun Y，Zhang W. Study on vibration characteristic of thirdorder shear deformation theory of plate. Journal of Dynamics and Control，2014，12（1）：50～55（in Chinese））

5 Plagianakos T S，Saravanos D A. High-order layerwise finite element for the damped free-vibration response of thick composite and sandwich composite plates. International Journal for Numerical Methods in Engineering，2009，77 （11）：1593～626

6 Brischettoa S，Carrera E，Demasi L. Improved bending analysis of sandwich plates using a zig-zag function. Composite Structures，2009，89（3）：408～415

7 XiaoYuLi，Dahsin Liu. Generalized laminate theories based on double superposition hypothesis. International Journal for Numerical Methods in Engineering，1997，40（7）：1197 ～1212

8 Wu Z，Chen b R G，Chen W J. Refined laminated composite plate element based on global - local higher-order theory. Conmposite Structures，2005，70（2）：135～152

9 吴根勇，和兴锁.旋转复合材料板的动力学性能研究.振动与冲击，2008，27（8）：149～154（Wu G Y，He X S，Deng F Y. Dynamic analysis of rotating composite plate. Journal of Vibration and Shock，2008，27（8）：149～154 （in Chinese））

10 Pan K Q，Liu J Y. Dynamic investigation on composite flexible multi - body system considering thermal effect. Journal of Shanghai Jiaotong University，2010，15（4）：414～422

11 Mohamad S. Qatu. Vibration of laminated shells and plates. San Diego：Elsevier，2004：7～12

12 Pagano N J. Exact solutions for composite laminates in cylindrical bending. Journal of Composite Materials，1969，3（3）：398～411

13 Pagano N J. Exact solutions for rectangular bidirectional composites and sandwich plates. Journal of Composite Materials，1970，4（1）：20～34

Received 29 October 2014，revised 17 December 2014.

*The project supported by the National Natural Science Foundation of China（11272203，11132007）

TATIC AND DYNAMINC ANALYSIS OF LAMINATED PLATE MULTIBODY SYSTEM BASED ON GLOBAL-LOCAL HIGHER ORDER SHEAR DEFORMATION THEORY*

Tian Lizhi†Liu Jinyang
（Shanghai Jiao Tong University，Shanghai 200240，China）

AbstractBased on the higher order shear deformation theory，the global-local 1，2-3 mode is derived in this paper. Given the conditions of the continuity of in-plane deformation and shear stress，as well as the free conditions of the upper and lower surfaces，the number of the independent variables for each node of laminated plate is reduced to 13，which is independent of the number of laminate layers. The displacement mode is then developed through rigid-flexible coupling dynamics for laminated plate mutibody system. Based on the principle of virtual work，the dynamic equations for mutibody system are established through the hybrid coordinate formulation，

where the continuity of the interlaminar stress is taken into consideration for laminated plate. The global-local 1，

2-3 displacement mode is obtained and verified against the exact solution in statics example. Finally，the comparison of the results obtained by the proposed method and the traditional method for laminated plate mutibody system illustrates the necessity of considering the continuity of interlaminar shear stress in simulation of laminated plate mutibody system.

Key wordsglobal-local higher order theory， continuity of interlaminar shear stress， laminated plate mutibody system， stress analysis

DOI：10. 6052/1672-6553-2015-021

通讯作者†E-mail：tlz19901216@163. com

Corresponding author†E-mail：tlz19901216@163. com