船舶推进轴系校中对轴系振动影响分析

杨俊王隽 王刚伟

（武汉第二船舶设计研究所，武汉 430064）



船舶推进轴系校中对轴系振动影响分析

杨俊†王隽 王刚伟

（武汉第二船舶设计研究所，武汉 430064）

摘要随着船舶振动噪声要求的提高，现有的静态校中设计方法不再适用，需要考虑轴系校中过程中不对中量对轴系振动的影响.通过对弹性联轴器处三种不对中型式进行受力分析，获得了不对中激励力数学模型，通过台架试验验证了数学模型的准确性.研究表明：轴系不中激励作用下，1倍频和2倍频以及通频振动计算结果与台架试验相对误差小于20%；校中过程中弹性联轴节处不对中量绝对值越大，所产生的激励的幅值越大，造成的振动也越大.

关键词轴系校中， 轴系振动， 不对中激励， 弹性联轴器

2015-03-20收到第1稿，2015-06-05收到修改稿.

引言

目前所广泛使用的各种轴系校中方法，都是从静力学角度出发，将轴系敷设为某种状态，保证各轴承获得较好的载荷分配，使轴段应力在设计允许范围内，确保轴系强度满足安全运行的要求.这些校中方法都没有考虑校中对轴系振动的影响.随着船舶振动噪声要求的提高，通过轴系校中对轴系振动影响的研究，掌握校中对振动影响规律是十分必要的.

船舶推进轴系由刚性联轴器和弹性联轴器联接，按照目前的静力学校中方法安装的轴系，联轴器两侧的法兰存在不对中量，根据联轴器类型的不同，不对中所产生的影响作用也不同［1 -4］.刚性联轴器处的不对中仅对轴承的静载荷产生影响；弹性联轴器处的不对中，会产生周期性的激励力，引起轴系振动［3，5 -7］.该激励力的幅值及频率与弹性联轴器的刚度、不对中量的大小以及轴系转速有关［5，8 -9］.本文通过对弹性联轴器处三种不对中型式进行受力分析，获得了不对中激励力数学模型，通过台架试验验证了数学模型的准确性.

1 轴系校中产生的不对中激励

1. 1 不对中激励的形式

船舶推进轴系各主轴之间由联轴器联接，以传递功率和扭矩，联轴器分为刚性联轴器和弹性联轴器.刚性联轴器两法兰之间通过铰制螺栓紧固，联接后各段主轴之间仍是同一根旋转中心线，因此不对中量仅对轴承间的静态载荷分配产生影响.弹性联轴器两端的法兰分别与相应的轴段联接，由于其弹性特征，联接之后艏艉两端轴线之间仍然存在一定的径向位移、偏角位移或综合位移等误差，使得联轴器两端的轴线不重合，这是造成轴系不对中激励的直接原因.如图1所示，联轴器之间的不对中可分为：平行不对中、角度不对中以及这两者的组合.

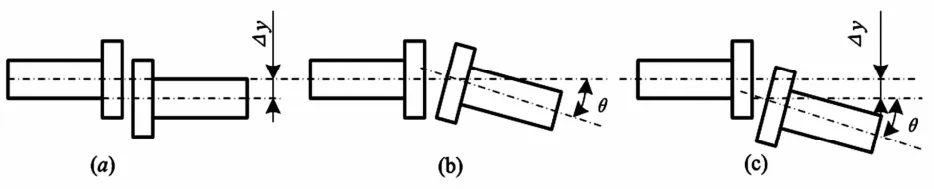
图1 不对中激励的型式Fig. 1 Misalignment model

1. 2 平行不对中

当联轴器两侧存在平行不对中时，联轴器两侧转子的不对中激励作用体现为在联轴器两端节点加受到了额外的力矩MX1，MX2，MY1，MY2，如图2所示.

图中：ΔX1，ΔX2是节点1在X，Y方向的位移不对中量；ΔY1，ΔY2是节点2在X，Y方向的位移不对中量；Z3为联轴器两侧结合处的中心距离.

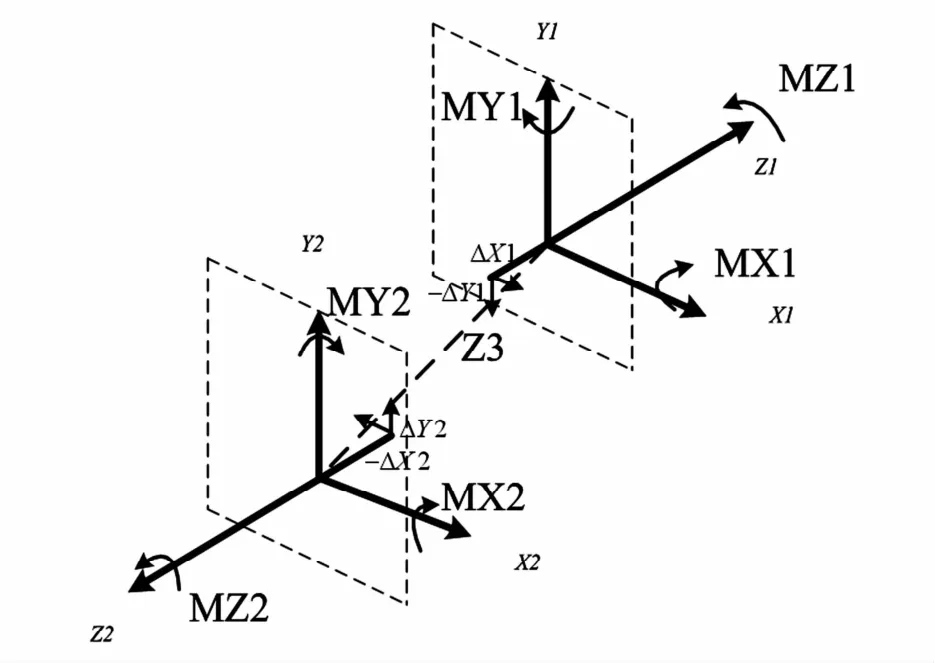
图2 平行不对中所受力矩作用示意图Fig. 2 The schematic diagram of parallel misalignment torque

而作用力矩中包含传递扭矩的分量以及联轴器弯曲引起的力矩，如图3所示.

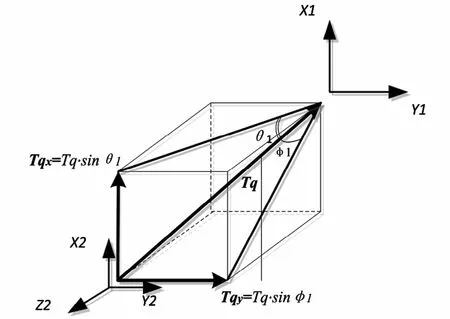
图3 平行不对中受力分析Fig. 3 The schematic diagram of parallel misalignment force

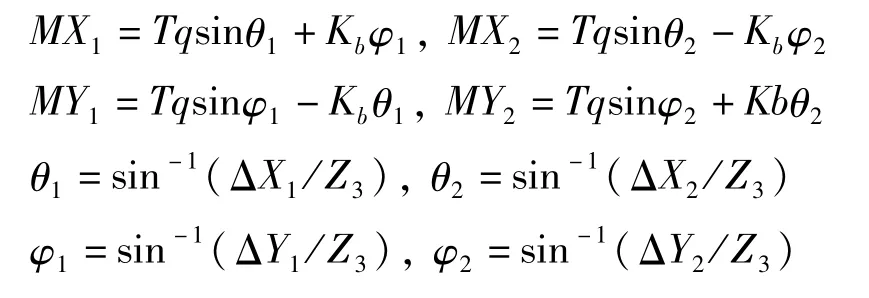
以上的反作用力矩以反作用力FX1，FX2的形式在轴系上作为不对中激励力传递，如下式所示.

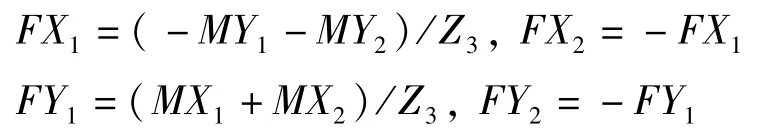
1. 3 角度不对中

存在角度不对中时，联轴器两侧转子的不对中激励作用体现为在联轴器两端节点加受到了额外的力矩MX1，MX2，MY1，MY2，如图4所示.其中，θ是角度不对中量.

作用力矩中包含传递扭矩的分量以及联轴器弯曲引起的力矩，如图5所示.

图4 角度不对中所受力矩示意图Fig. 4 The schematic diagram of angular misalignment torque

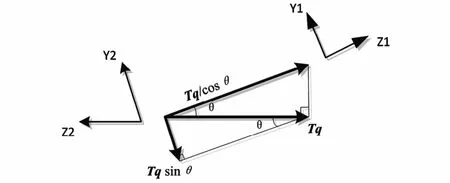
图5 角度不对中受力分析Fig. 5 The schematic diagram of angular misalignment force

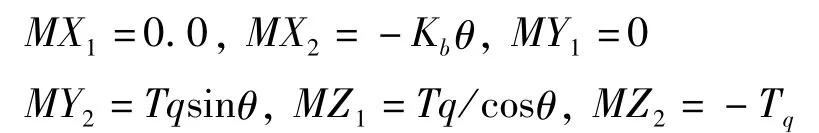
以上的反作用力矩以反作用力FX1，FX2的形式在轴系上作为不对中激励力传递，如下式所示.

1. 4 不对中的激励力

上面提到的反作用力与反作用力矩都是静止轴系的静态负荷.对于工作中的轴系，动态负荷表现为周期性的正弦函数.考虑在相应节点作用角速度为1Ω和2Ω的时变反作用力.轴系不对中在联轴器两端节点引起的额外载荷向量｛Q1c｝和｛Q2

c｝，具体表达式如下：

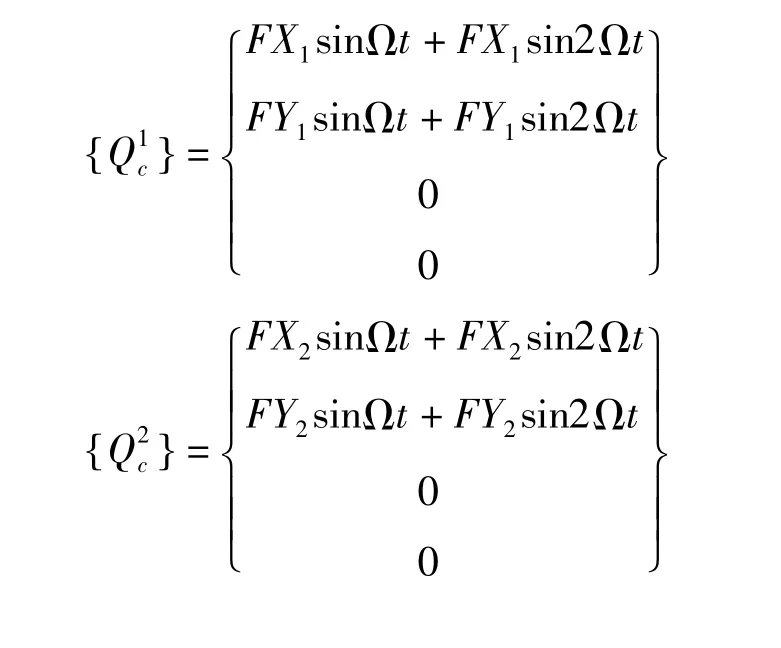
所以，当平行不对中和角度不对中两种不对中形式同时存在时，不对中激励力是二者的叠加，如下所示：

将Qc表达形式加入到系统动力学方程的右侧，即可得到考虑联轴器不对中激励影响的轴系动力学方程.

2 轴系动态响应计算

2. 1 船舶轴系有限元建模

实际转子是一个质量连续分布的弹性系统，具有无穷多个自由度.在将有限元方法应用于转子动力学时，通常将转子简化为具有若干个集总质量的多自由度系统.沿转子轴线把转子质量和转动惯量集总到若干个节点处，这些节点一般选择在叶轮、轴颈的中心、联轴器、轴的截面有突变处以及轴的段部等，并按照顺序编号，轴承一般安排到节点处.本文根据船舶轴系转子结构和轴承位置，将转子划分为12段共13个节点，如图6所示.

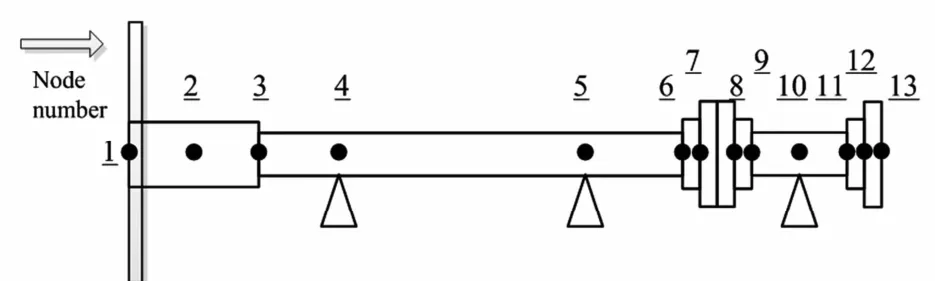
图6 转子轴承系统的离散化Fig. 6 The discretization of the rotor-bearing system

2. 2 系统运动方程

2. 2. 1 转子单元运动方程

图7 转子单元模型Fig. 7 Rotor unit model

转子单元可视为欧拉梁，如图7所示.每个单元有两个节点，每个节点有四个自由度，分别是节点在水平方向的位移x、竖直方向的位移y、绕水平轴转角θx、绕竖直轴转角θy.节点i处位移向量为：

节点i与节点i +1组成单元i的位移向量为：

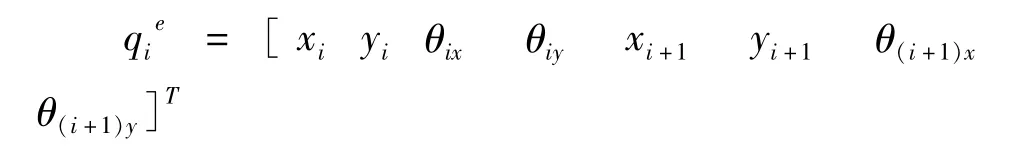
定转速下的转子单元的拉格朗日运动方程如下：

其中转子单元位移质量矩阵为：

转角质量矩阵为：

阻尼阵为：

弯曲刚度矩阵为：

轴向载荷刚度矩阵为：

m为单元线密度Kg/ m，l为单元长度，r为单元半径，E为单元弹性模量，I单元直径转动惯量，P为轴向载荷.

｛Qe｝为力向量，可以包含作用在转子单元上的不平衡质量，外载等.

2. 2. 2 轴承处转子单元运动方程

线性轴承处转子单元的运动方程为：

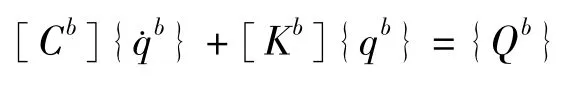
其中位移向量为：

刚度矩阵为：

阻尼矩阵：

2. 2. 3 系统运动方程

以上分别对转子单元和轴承处转子单元进行运动分析，形成了各单元的运动方程.将各个部件的质量阵、刚度阵、阻尼阵分别合并，并将各部件受力等效合并，得到整个系统的动力学方程：

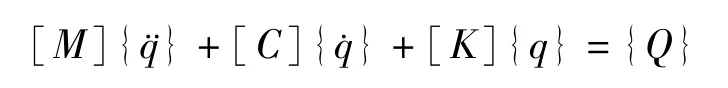
其中｛Q｝包含各部件的重力，不平衡激励、轴系不对中造成的激励以及其它外载.

3 轴系校中对轴系振动响应影响计算

以图8所示轴系试验台架为对象，开展轴系校中对轴系动力学响应影响的规律研究.通过改变轴承位置，来获得不同的轴系校中状态，计算不同校中状态下，联轴器处的激励力，并利用有限元法，进行轴系在此不对中激励作用下的响应计算.

图8 试验台架布置简图Fig. 8 Experiment set-up

计算条件：艉端载荷是20kg，通过改变2＃轴承的标高来调整轴系校中状态，调整范围-1～1mm，计算得到不同校中状态时，弹性联轴器两端节点的不对中量，计算结果如表1所示.计算取扭矩Tb为6000N·m，联轴器刚度Kb为107N·m/ rad，联轴节厚度为40mm.

4 轴系校中对轴系振动影响台架试验

4. 1 试验台架及测试系统组成

4. 1. 1 试验台架组成

试验台架包括以下基本部分：驱动系统，润滑系统，轴承系统，测量系统，以及基础平台等.该台架为两跨三支承轴系，三个轴承为油润滑轴承，台架艉部装有圆盘，以模拟螺旋桨悬臂载荷.通过改变圆盘质量，可对不同载荷条件下轴系运行情况进行试验，本试验中加载盘重量选择20kg.台架配置的标高调整系统，可在不停机的条件下，对轴承标高进行精确调整，以测量不同校中状态下，该联轴器处的不对中对轴系振动的影响.

4. 1. 2 轴系振动测量系统组成

试验台架轴系振动测试系统主要包括电涡流传感器、转速传感器、速度传感器、信号采集器、工控机等.试验中共选择三个振动测点，分别固定于三个轴承的轴承座上，每个测点处安装两个互为直角的电涡流传感器，具体布置如图9所示.

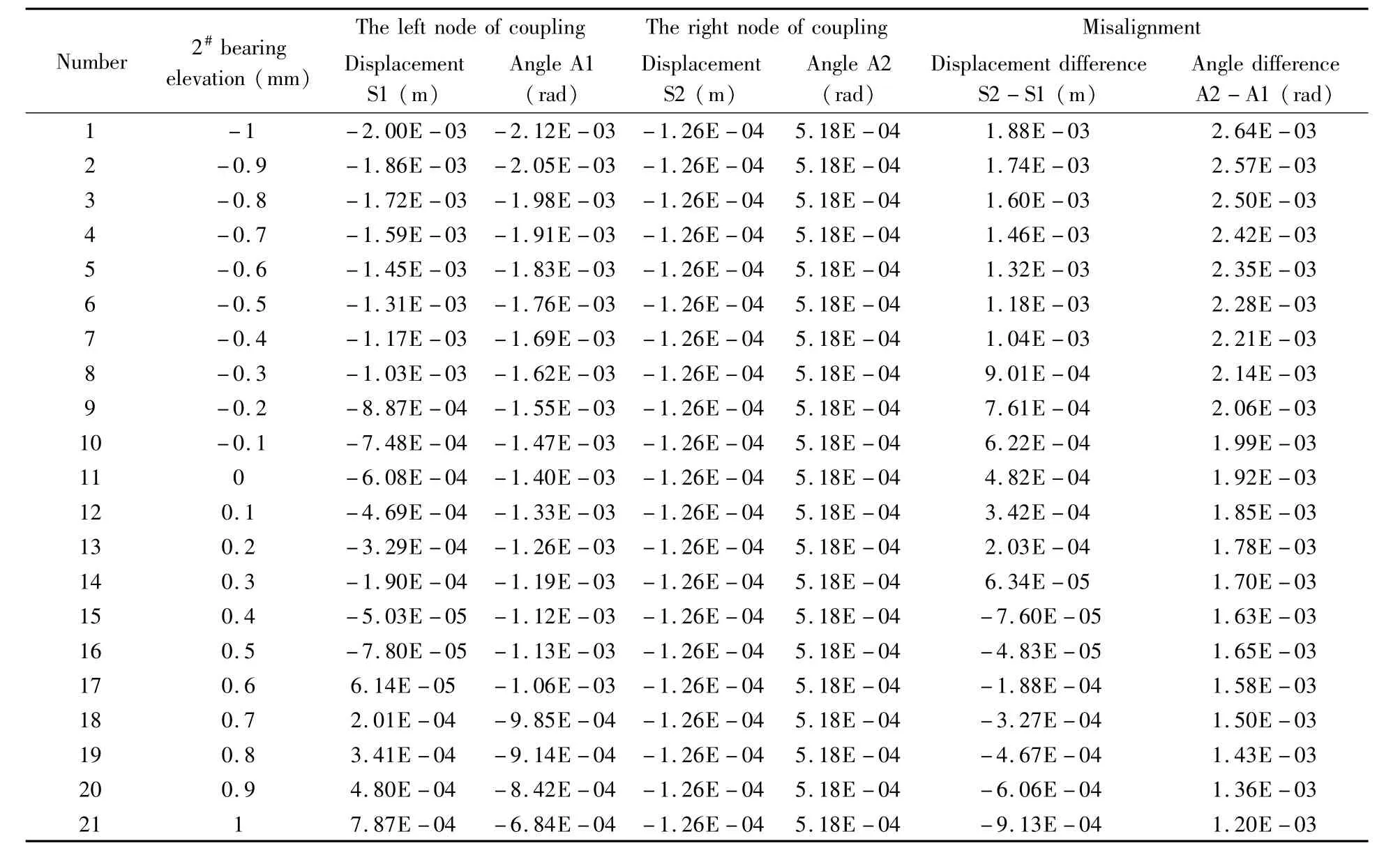
表1 2＃轴承标高变化时联轴器不对中量变化Table 1 coupling misalignment varying with 2＃bearing elevation

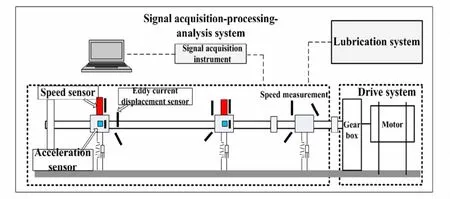
图9 轴系振动测量系统示意图Fig. 9 The measurement systemof shaft vibration

图10 涡流位移传感器的安装Fig. 10 Installation of eddy current displacement sensor

4. 2 台架试验内容

在试验轴系艉部加载20kg轮盘模拟推进器的悬臂载荷，试验在500r/ min的定转速下完成.

a）首先利用激光对中仪，将三个轴承调整至等高状态，及直线校中状态；

b）测量此状态下的轴系振动情况；

c）调整2＃轴承的标高，将其降低0. 5mm，测量此状态下的轴系振动情况；

d）调整2＃轴承的标高，将其抬高0. 5mm，测量此状态下的轴系振动情况.

4. 3 试验结果与理论计算对比分析

4. 3. 1 直线校中状态对比分析

通过试验，得到试验轴系在直线校中状态下转速为500r/ min时动力学响应. 2＃轴承处振动时间历程图和频域图如图11、图12所示.

从上面试验和计算结果的对比可以看出计算和试验振动响应的线谱频率基本一致，主要是一倍频和二倍频.

4. 3. 2 2＃轴承抬高0. 5mm试验

通过试验，得到轴系在直线校中状态基础上2＃轴承标高上升0. 5mm、转速为500r/ min时轴系动力学响应，各轴承处振动时间历程图和幅值图如图13、图14所示.

从上面试验结果和计算结果的对比可以看出计算和试验振动响应的线谱频率一致，主要是一倍频和二倍频.

图11 2＃轴承响应时域图Fig. 11 Time response graph of 2＃bearing

图12 2＃轴承响应频域图Fig. 12 Frequency response graph of 2＃bearing

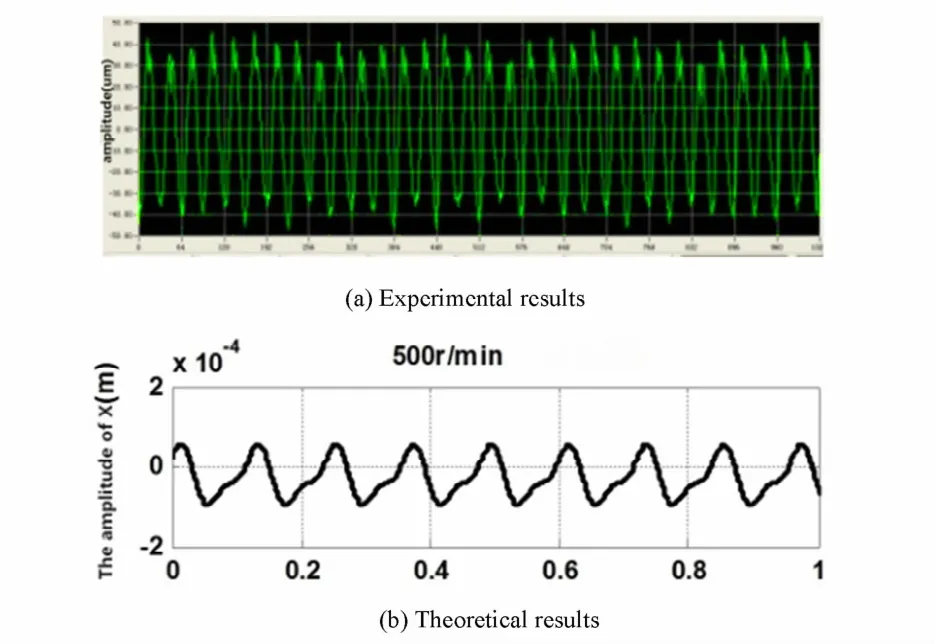
图13 2＃轴承响应时域图Fig. 13 Time response graph of 2＃bearing

4. 3. 3 2＃轴承标高降低0. 5mm试验

通过试验，得到轴系在直线校中状态基础上2＃轴承标高下降0. 5mm、转速为500r/ min时轴系动力学响应，各轴承处振动时间历程图和幅值图如图15、图16所示.

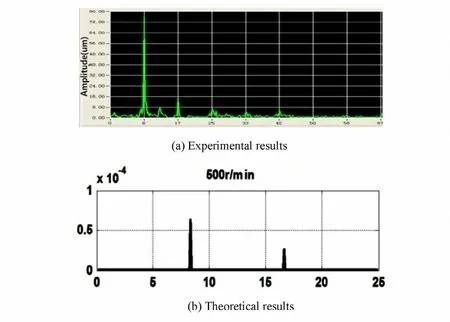
图14 2＃轴承响应频域图Fig. 14 Frequency response graph of 2＃bearing

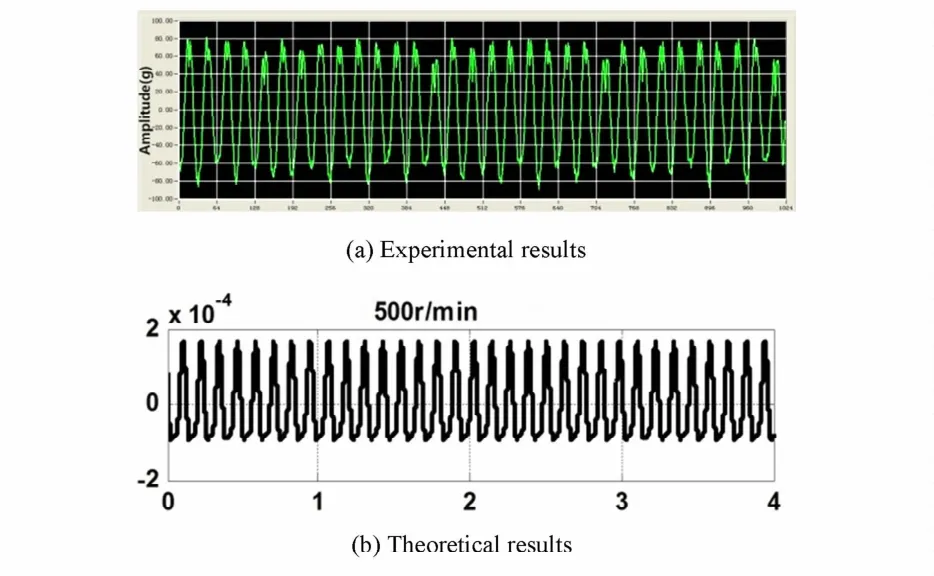
图15 2＃轴承响应时域图Fig. 15 Time response graph of 2＃bearing

图16 2＃轴承响应频域图Fig. 16 Frequency response graph of 2＃bearing

从上面试验结果和计算结果的对比可以看出计算和试验振动响应的线谱频率一致，主要是一倍频和二倍频.

4. 3. 4 试验结果与计算结果对比

将台架试验所测量的不同校中状态下各轴承处的振动位移幅值与理论计算结果进行对比，结果如表2所示.

表2 试验结果与理论计算结果对比Table 2 The comparison of experimental and theoretical results

5 结论

通过轴系校中对轴系振动影响分析研究，可以得出以下结论：

（1）轴系校中状态变化导致弹性联轴器艏艉法兰产生轴系不对中，会产生周期性的附加激励，即不对中激励.

（2）轴系不对中激励受不对中量绝对值大小影响，不对中量绝对值越大，激励的幅值越大.

（3）台架试验结果表明，不同校中状态下，轴系1倍频、2倍频以及通频的振幅计算结果与台架试验结果相对误差小于20%，表明不对中激励数学模型的准确性满足工程应用要求.

参 考 文 献

1 刘占生，赵广，龙鑫.转子系统联轴器不对中研究综述.汽轮机技术，2007（5）：321～325（Liu Z S，Zhao G，Long X. Survey of the research on coupling with misalignment of rotary machinery. Tubine Technology，2007（5）：321～325（in Chinese））

2 Xu M，Marangoni R D. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance part I：theoretical and model analysis . Journal of Sound and Vibration，1994，176（5）：663～679

3 赵广.转子-联轴器-轴承-隔振器系统耦合动力学特性研究.哈尔滨：哈尔滨工业大学，2009（Zhao G. Study on coupled dynamics of rotor-coupling-bearing-isolator system. Harbin：Harbin Institute of Technology，2009（in Chinese））

4 Xu M，Marangoni R D. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance part II：experiment validation. Journal of Sound and Vibration，1994，176（5）：681～691

5 Patel T H，Darpe A K. Experimental investigations on vibration response of misaligned rotors. Mechanical Systems and Signal Processing，2009，23（7）：2236～2252

6 Patel T H，Darpe A K. Vibration response of misaligned rotors. Journal of Sound and Vibration，2009，325（3）：609～628

7 Sekhar A S，Prabhu B S. Effects of coupling misalignment on vibrations of rotating machinery. Journal of Sound and Vibration，1995，185（4）：655～671

8 Parbhakar S，Sekhar A S，Mohanty A R. vibration analysis of a misaligned rotor-coupling-bearing system passing through the critical speed. Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2001，215（2）：1417：1428

9 赵广，刘占生，陈锋，王永亮.转子-联轴器-轴承-隔振器系统不对中及锁频故障实验研究.动力学与控制学报，2009，7（2）：171～176（Zhao G，Liu Z S，Cheng F，Wang Y L. Experiment research on misalignment and frequency-locking trouble of rotor-coupling-bearing-isolator system. Journal of Dynamics and Control，2009，7（2）：171～176（in Chinese））

Received 20 March 2015，revised 5 June 2015.

ANALYSISON THE EFFECT OF MARINE PROPULSION SHAFTING ALIGNMENT ON ITSVIBRATION

Yang Jun†Wang Jun Wang Gangwei
（Wuhan Second Ship Design and Research Institute，Wuhan 430064，China）

AbstractWith the improvement of marine vibration index，the current static shafting alignment method is not yet suitable. The effect of shafting misalignment on rotating system vibration is not clear. Based on the mechanics analysis on elastic coupling of three different types of misalignment，the dynamic models of misalignment excitation are first established，and this dynamic model is also verified by bench test. The results show that under the excitation of shaft misalignment，the relative errors between the simulation results for the situations of synchronous harmonic，second harmonic and peak-peak vibration and the bench test data are less than 20%. Moreover，it is found that the increasing misalignment of elastic coupling results in strong vibration，accompanying with increasing excitation amplitude.

Key wordsshaft alignment， shaft vibration， misalignment excitation， elastic coupling

DOI：10. 6052/1672-6553-2015-041

通讯作者†E-mail：hityj@163. com

Corresponding author†E-mail：hityj@163. com