纬编提花绗缝织物凹凸曲面的测量及三维建模

金兰名， 蒋高明， 丛洪莲

(江南大学 教育部针织技术工程研究中心, 江苏 无锡 214122)

纬编提花绗缝织物凹凸曲面的测量及三维建模

金兰名， 蒋高明， 丛洪莲

(江南大学 教育部针织技术工程研究中心, 江苏 无锡 214122)

针对纬编提花绗缝织物花型图案复杂、织物尺寸较大、多层结构易致仿真困难等特点，为节省设计与生产过程中造成大量时间、人力、物力资源的浪费，试图建立常规绗缝提花织物曲面模型并进行计算机仿真。综合考虑织物面密度和生产工艺的影响，共试织10种不同规格的织物样品进行凹凸效果分析，对连接纱引起的织物表面凹凸变化规律进行数据采集和计算，参考泛克里格法插值获得初步仿真结果，根据4块试样凹陷曲线方程对仿真过程进行改进，构建纬编提花绗缝织物三维模型。结果对于具有立体效果的织物计算机仿真有一定指导意义，为三维织物仿真系统的建立提供理论参考。

纬编； 绗缝织物； 三维建模； 曲面建模

提花绗缝织物较好的透气性、环保性和美观大方的图案使其在服装、家纺领域得到广泛运用。这种绗缝织物由于衬纬纱的存在产生了一定厚度,前后编织的连接纱将织物面纱、地纱和衬纬纱连接固定，并根据不同规格形成凹凸效果不等的立体感，因此，较为平面的花型设计图案与相对立体的最终织物产生了较大差距。

近年来,织物三维仿真技术研究已经屡见不鲜，Peirce模型及其衍生纱线模型、结构可控的非均匀有理B样条曲线、NURBS曲线等理论研究以线圈结构为主，并不适合提花绗缝织物小线圈、大提花、组织简单、立体感强[1]的特点，建立单个线圈模型更易降低仿真的真实感和速度。

本文研究针对提花绗缝织物的特点，提出建立三维凹凸曲面模型对此类织物进行计算机仿真。共试织10种相同原料、不同规格的织物，通过测试其凹凸效果得出相应数据及曲线方程，建立不同织物的曲面模型。本文实验是织物三维模拟仿真的完善，对提花绗缝等具有凹凸效果的织物三维模拟系统的设计开发有一定指导意义。

1 提花绗缝织物的仿真及方法

1.1 提花绗缝织物的仿真

提花绗缝织物由电脑提花圆机织造，其中图案开发和上机打板2个环节大都浪费大量的人力、物力和时间。主要问题为织物表面凹凸效果预判错误，颜色、图案搭配不当，织物密度及机器参数设置造成图案变形等。主要原因是提花绗缝织物的花型设计和织物实物的对比相距甚远，织物最终效果难以预估。如图1所示纬编提花绗缝织物，花型设计图可为以像素为单位的bmp格式文件生成，其与实际织物花型边缘形成的凹凸效应差距较大。如能通过三维建模预测不同面密度的设计意匠图，将减少产品开发的时间和损耗，有助于提升企业产品开发能力。

1.2 提花绗缝织物的仿真方法

纬编提花绗缝织物线圈较小，编织工艺简单，原料纱线较细，立体感强，此类织物在设计过程中的预测重点是花型图案的凹凸效果、颜色搭配、图案大小。从二维角度模拟织物外观，削弱了织物外观的真实感效果[2]，建立线圈模型更易降低仿真的真实感和速度，因此，本文提出根据三维曲面模型进行织物模拟，从织物织造方法及产生凹凸效果的原因入手,分析影响织物外观效应各因素之间的关系,以仿真真实度与仿真时间作为主要指标对织物仿真中的若干问题进行研究。

2 实验设计

提花绗缝织物的原料可分为面纱、提花纱以及衬纬纱。根据对织物面密度的要求，在织物组织中添加不同规格的涤纶网络丝增加织物的立体感[3]。

2.1 面料样品

本文选用德国迈耶·西公司生产的OVJA 1.6E电脑提花圆机进行小样试织。采用28 tex人造棉纤维作为正面纱，16.7 tex/76 f 拉伸变形丝(DTY)作为反面纱，搭配66.7 tex/192 f 拉伸变形丝作为衬纬纱。这种具有立体效果的双面织物，织物的2个表面分别在针筒和针盘针上编织，内衬纱的增减使织物产生不同的厚度变化，根据不同工艺要求通过电脑选针使反面纱线在正面成圈,起到连接前后面及衬纬纱的作用。

实验选择试织10种常见规格的织物，如表1所示。分为5种纱线配置方案织造，面密度为630 g/m2的样品是为目前机器批量生产的最大值。

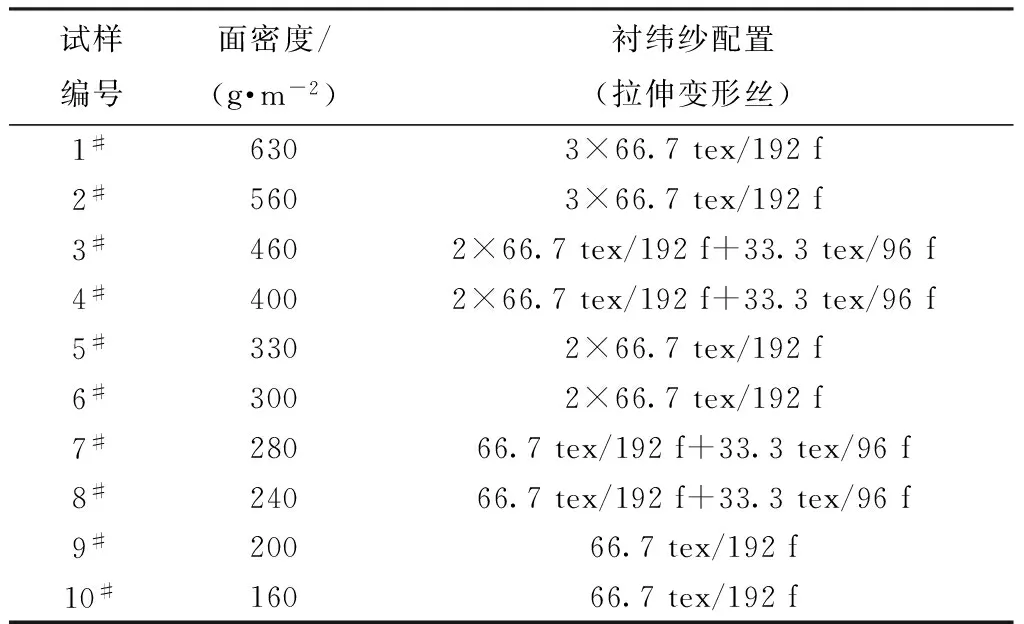
表1 试样1#～10#规格表Tab.1 Specifications of sample 1#-10#

2.2 提花绗缝纬编织物厚度的测量与计算

为使实验结果更加准确，10块试样采用相同工艺进行编织。图2示出织物提花示意图。黑色意匠格代表提花纱线，为不影响相邻2个提花纱线圈的相互作用，选择间隔1.5 cm的方式进行织造。

织物曲面厚度差即曲面织物最大曲面形变相对于参照面的最大距离。曲面织物高度如图3所示。在曲面织物中间接近高度最大的地方使用厚度仪多次测量高度，取其最大值。厚度差的测量和计算公式如下:

h=A1-A2/2

式中：h为织物的厚度差；A1和A2分别代表织物最大厚度和最小厚度，mm。h值越大,织物的立体感越强。

曲面翘曲度。曲面织物的曲面形变表达是其重要指标，评价指标在现有纺织品评价体系中还不完善，参考伍杰一[4]提出曲面织物的曲面翘曲度概念并运用公式表示如下：

R=h/l

式中：R为曲面织物的最大翘曲度；h为厚度差，mm；l为曲面的投影长度,mm。

3 实验分析

3.1 试样数据分析

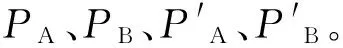
3.2 数据测量及计算

为准确获得曲面投影长度求得试样曲面翘曲度，需参考实际织物的图像。将切片后的织物截面运用超景深显微镜取像后转为阈值为110的无彩色像素图像，其轮廓较为清晰，如图5所示。

由图5可看出，点A为达到曲线EA峰值首个像素点，点E为凹陷处首个像素点，EF为水平方向，直线AB平行于EF，BD垂直于EF且平行于AC，根据已知织物曲面的厚度差数值和像素的数量之间的关系,可计算曲面投影长度:

l=l1h/h1

式中：l为曲面变化范围；h为织物最厚处；h1为AC像素数量；l1为AB像素数量。

本次仿真选择1#、3#、6#、8#试样进行像素测量和三维建模，由表3所示，曲面翘曲度R随投影长度和织物厚度差的增加而增加。

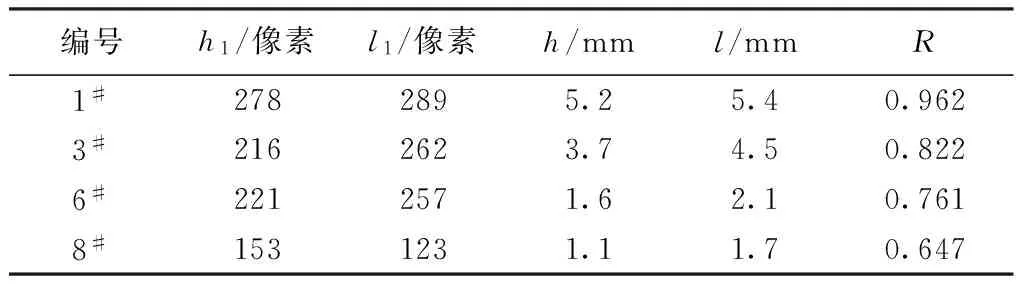
表3 1#、3#、6#、8#试样像素测量结果Tab.3 Pixels measurement results of sample 1#, 3#, 6# and 8#

4 纬编绗缝提花织物三维建模

4.1 曲面三维模型的初步建立

确定提花绗缝织物4块试样的曲面数值后，利用数字高程模型DEM(digital elevation model)给定二维数值高程值进行初步仿真模拟，模型结构简单，易于构网，存储量小，分析计算简便,适用于提供基本的数据支持地形建模的过程。具体流程[5]如图6所示。

通过在X和Y方向上按等距离方式记录断面上点的坐标,利用一系列在X,Y方向上等间隔排列的地形点的高程Z表示表面形态,形成矩形格网[6]。在数学上可表示为一个矩阵,表示区域D上地形的三维向量有限序列，用函数形式描述为：

Vi=(Xi,Yi,Zi) (i=1, 2,…,n)

其中：(Xi，Yi∈D)是平面坐标；Zi是(Xi，Yi)对应的高程。

高程数字模型内插的具体方法较多，考虑到绗缝织物凹陷非剧烈起伏，本文中使用相对误差较小的泛克里格方法来实现。泛克里格(universal kriging)假设数据中存在主导趋势，且该趋势可用1个确定的函数或多项式来拟合[7]。在此方法中， 预测值z(S0) 由2部分组成。一部分是m(S0)估计值，通过不同环境解释变量对主变量的回归估计，S0表示待估测点位置；第2部分是通过克里格插值残差e(S0)。泛克里格估计公式[8]如下：

z(S0)=m(S0)+e(S0)

式中：βk表示趋势模型的估计参数，本研究中选择普通最小二乘法进行估计；wi表示不同采样点位置残差的权重，此权重由残差半变异函数确定；e表示回归模型的残差。

选择其中4个试样进行建模，由于离散数据易引起模型异常，因此每个试样选择以织物凹陷处投影范围为半径的圆上的1#～9#个点为坐标值(X，Y)，具体如表4所示。

通过泛克里格插值确定圆内各点高程值(Z)后即可得出建模结果。如图7所示利用数字高程模型制作的立体模型。可判断厚度差异会影响提花绗缝织物的立体效果，通过相对简单、准确的数值能够对其最终效果进行初步仿真。运用DEM模拟的织物虽然可基本表示其凹凸效果，但DEM本身是自然地表的逼近而非数学表达，其误差来源于离散高程点的采样误差和插值或拟合所产生的逼近误差。由图还可看到连接点处凹陷过于理想，仅凭借曲面翘曲程度内插建模不能完全展现织物形态。DEM的内插模型由离散的格网数据直接构建的连续曲面，不符合由点到线、再由线到面的构造机理[9]，因此，由实际织物翘曲范围坐标点构成的曲线将更准确地展现绗缝织物的凹凸变化。

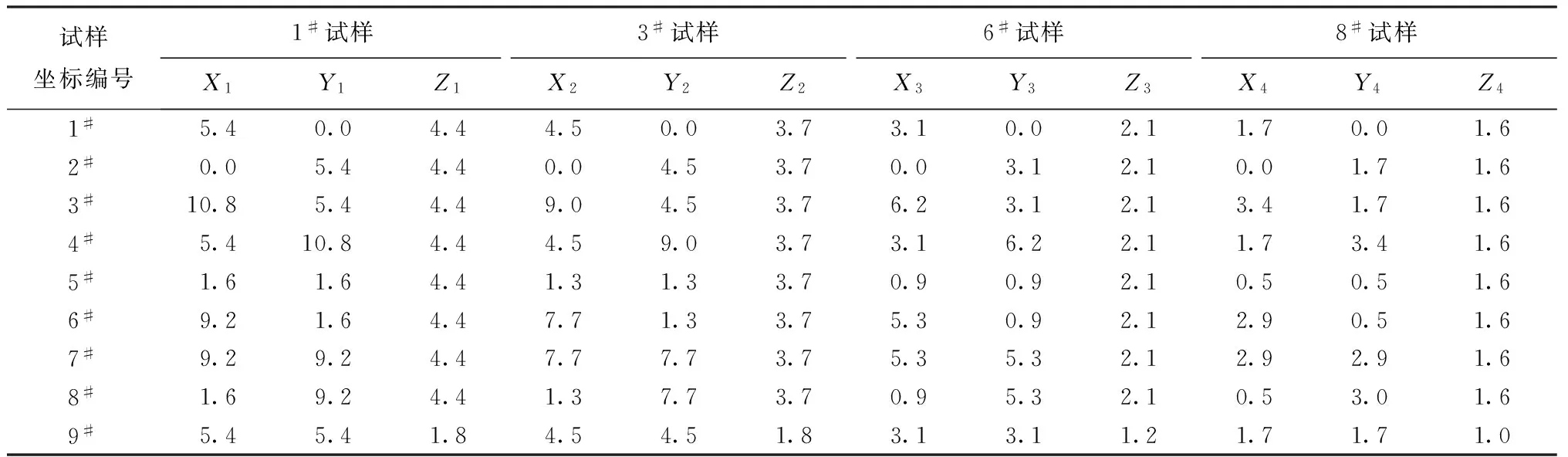
表4 1#，3#，6#，8#试样坐标值Tab.4 Coordinate figure (X,Y,Z)of sample 1#，3#，6# and 8#

4.2 纬编提花绗缝织物的三维建模

由上述仿真试验可知，单纯加入高程值的模型对后续织物真实感的模拟与预测不能起到基础作用，因此，运用织物翘曲变化规律建模，按照凹陷区域计算出织物真实凹陷变化曲线方程，借鉴DEM插值的算法进行建模。

图8示出织物凹陷处三维示意图。假设点O为织物最小厚度的一点，OM为曲面投影范围，N为纵向对应曲线上的一点，即织物厚度为MN。以OZ为中轴线，ON旋转一周形成三维凹陷面，即织物连接点处形成的模型，故以此能准确分析织物连接区域的厚度变化。

具体建模流程图如图9所示。首先对截面图进行二值化处理，使凹陷面能够被清晰鉴别。将切片后的织物截面拍照后转为阈值为110的无彩色像素图像，其轮廓较为清晰。根据已知织物曲面的厚度差数值和像素数量之间的关系,计算曲面的变化范围数值。本文基于MatLab获取各点平面坐标。然后，对曲面边缘进行快速检测，计算机将黑色像素点定义数值为0，白色像素点定义数值为1，检索时只针对0、1交界处的像素点进行查找，获取点N坐标值(m,z)。随后，计算机根据获取的数据进行快速的曲线拟合，如图10所示，获得曲线方程。

最终建立织物曲面曲线方程，方法如下：

以3#试样为例，假设每一个连接纱线圈造成的曲面凹凸范围形成一个半径为r的圆，计算其内部凹凸变化[10]。每个曲面坐标通过以下方程确定:

x=msinθ

y=mcosθ

z=0.003 6m3- 0.160 9m2+ 3.266 7m-3.106 8

式中：r为曲面凹凸范围所在圆的半径；m为半径内的任一点，0

提花绗缝织物的建模以每个连接纱线圈及其凹凸曲面为单元建立，图11示出不同角度的3#试样三维模型。图中0°角下的为截面图。通过查看不同角度的织物凹陷变化曲线可知，与线圈仿真相比，曲面建模所得仿真结果更加接近实际织物。配合运用光照模型和纹理映射等方式可增强织物表面真实感。图12示出运用文中所述方法对某斜纹提花绗缝织物进行建模和真实感模拟，可从不同角度清晰辨别织物提花纱线造成的凹凸表面，效果较为逼真。

5 结 论

针对线圈建模不适合提花绗缝织物等具有立体效果的织物，线圈过小、织物仿真面积过大以及计算机处理速度为影响最终效果的重要因素的问题，本文对提花绗缝织物的曲面凹凸效果进行数据分析并建立模型，目的是建立此类织物的三维模型，经研究得出以下结论：1)通过10种不同面密度的织物实验发现，织物翘曲度是决定织物立体感的关键，织物凹凸曲面的测量有助于立体效果织物的仿真;2)运用高程数字模型(DEM)配合泛克里格插值算法可基本表现出由于厚度差引起的织物规则凹陷，但是由算法误差造成的曲面过于理想;3)通过建立凹陷区域曲线方程建立三维曲面模型，能够较全面地观察此类织物的特征，较好展现提花绗缝织物的凹凸效果。

通过研究实现了纬编提花绗缝织物的三维仿真，后续工作可针对不同工艺图案提花织物进行研究，并尝试建立三维立体提花织物的计算机仿真系统。

FZXB

[1] 李蓓蓓. 三维织物仿真的研究[D]. 上海：东华大学,2007:6-12. LI Beibei. 3-D fabric simulation research[D]. Shanghai：Donghua University, 2007: 6-12.

[2] 马凌洲. 计算机辅助织物创新设计与制作系统的研究与实现[D].杭州：浙江大学, 2005:9-13. MA Lingzhou. Fabric computer aided innovation design and manufacture system research and implementa-tion[D]. Hangzhou: Zhejiang University, 2005:9-13.[3] 李丽敏, 赵俐. 底板色块数对床垫面料表面凹凸感的影响[J].针织工业, 2010(9):8-10. LI Limin, ZHAO Li. The effect of soleplate color piece number of the mattress fabric to surface stereo-scopy [J].Knitting Industries, 2010 (9): 8-10.

[4] 伍杰一,赵敏. 织物组织对曲面机织物成型效果的影响[J].纺织科技进展, 2014(2):28-31. WU Jieyi, ZHAO Min. Fabric woven fabric is based on the forming effect[J]. Journal of Textile Science and Technology Progress, 2014 (2): 28-31.

[5] 张锦明. DEM插值算法适应性研究[D].郑州：解放军信息工程大学, 2012:20-24. ZHANG Jinming. DEM interpolation algorithm adaptability research[D]. Zhengzhou：the PLA Information Engineering University, 2012:20-24.

[6] 贺丹.不同分辨率DEM提取地形因子的适宜分析窗口研究[D]. 西安：西北大学，2012:17. HE Dan. Different resolution DEM extraction of terrain factors of appropriate window study [D]. Xi′an：Northwest University, 2012:17.

[7] 郭炳岐.基于Kriging方法的GPS高程拟合模型及其应用研究[D].西安：西安科技大学, 2008:23-24. GUO Bingqi. Based on the GPS elevation fitting model of Kriging method and its application research [D]. Xi′an：Xi′an University of Science and Technology, 2008:23-24.

[8] CRESSIE N A C. Statistic for Spatial Data[M]. New York: John Wiley & Sons, 1993: 151-172.

[9] 王耀革. 基于Coons曲面的规则格网DEM表面模型[J].测绘学报, 2008(5):217-222. WANG Yaoge. Based on the rules of Coons surface grid DEM surface model [J]. Journal of Surveying and Mapping, 2008(5):217-222.

[10] 邵昊.地质体的三维建模与可视化研究[D]. 武汉：中国地质大学, 2008:28-39. SHAO Hao. 3-D modeling and visualization of geological body research[D]. Wuhan: China University of Geosciences, 2008:28-39.

Determination and 3-D modeling of weft knitted jacquard quilted fabric with concave surface

JIN Lanming, JIANG Gaoming, CONG Honglian

(Engineering Research Center of Knitting Technology, Ministry of Education, Jiangnan University, Wuxi, Jiangsu 214122, China)

Focusing on the problems of weft knitted jacquard quilted fabric on complicated pattern, large fabric size and easy simulation of the multilayer structure of fabric, in order to save a great amount of time, manpower and material resources in the design and production processes, the curved surface modeling and computer simulation are performed on conventional weft knitted jacquard quilted fabric. Considering the effect of surface density and production process, 20 kinds of fabric samples with different specifications is subjected to the concave-convex effect analysis, data acquisition and calculation are performed on the concave-convex change rule of the fabric surface caused by connecting yarn, and the initial simulation result is obtained in reference to Universal Kriging. The simulation process is modified according to the concave curve equation of 4 samples, and the 3-D model of the weft knitted jacquard quilted fabric is established. The result provides guiding significance for the computer simulation of the fabric, and establishes a theoretical basis for the simulation system of 3-D fabrics.

weft knitted; quilted fabric; 3-D modeling; curved surface modeling

10.13475/j.fzxb.20150403407

2015-04-20

2016-02-17

国家科技支撑项目(2012BAF13B03)

金兰名(1988—)，女，博士生。主要研究方向为三维纬编提花织物的计算机仿真。蒋高明，通信作者，E-mail：jgm@jiangnan.edu.cn。

TS 186.2

A