含间隙和尺寸误差空间连杆引纬机构运动精度综合分析

张 雷， 贺 虎， 孔佳元

(浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

含间隙和尺寸误差空间连杆引纬机构运动精度综合分析

张 雷， 贺 虎， 孔佳元

(浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

为分析间隙和尺寸误差对引纬机构运动精度的影响,详细介绍了非连续接触模型和等效杆长理论的使用方法,针对空间连杆引纬机构中的空间四杆机构和平面四杆机构，在考虑制造误差和磨损或装配间隙的情况下，以概率分析方法和非连续接触理论为基础建立了运动学模型。运用MatLab的计算和仿真模块进行运动仿真，得出了相关曲线。详尽分析了机构的尺寸误差和间隙对整个机构运动输出的影响,在考虑构件误差和间隙影响时，剑头的输出误差比单独考虑1种影响因素时明显，且误差最大值都出现在速度的极大值点附近，可见间隙和构件误差对高速机构的影响尤为显著，此研究结果可为后续对空间连杆引纬机构的运动精度分析提供参考。

引纬机构； 非连续接触模型； 间隙； 等效杆长理论； 尺寸误差

随着纺织工业的发展，无梭引纬方式得到广泛应用，剑杆引纬、片梭引纬、喷水引纬和喷气引纬由于运动精度高和较强的产品适应性等优点得到纺织企业的青睐。引纬机构是剑杆织机的核心部分，对织机的性能起到决定性作用。近年来，引纬机构主要朝着广泛适应性、高速度、高精密性、高可靠性等几个方面发展。目前，国内引纬机构的主要类型有4种：共轭凸轮引纬机构、空间连杆机构、变导程螺旋引纬机构和差动轮系连杆机构，其中应用最为广泛的是空间连杆机构。

针对连杆机构的运动精度研究，文献[1]以概率论为理论基础，提出了针对铰间间隙研究的等效杆长方法；文献[2]考虑杆长尺寸偏差和铰间间隙以及磨损等因素，以飞机舱门为例对任意空间四杆机构进行了运动精度和可靠性分析；文献[3]运用拉格朗日方程对含间隙平面四杆机构进行了动力学和运动特性分析，建立了形式简单易于计算的矩阵形式的运动输出模型；文献[4]运用二维矢量表示的方法，对机器人关节间隙进行了深入研究，并以概率论为理论基础，建立了机器人输出末端点的概率密度函数，得出了关节间隙误差与机器人末端位置重复精度的约束关系；文献[5]针对含间隙平面四杆机构的运动时变可靠性(任意时刻机构误差是否超过允许范围)进行了综合分析，对含间隙和尺寸公差的空间连杆引纬机构的精度研究提供了依据，但是，国内对织机引纬机构的运动精度的综合分析的文献较少，对这方面的研究十分迫切。

本文针对高速空间引纬机构，考虑杆件设计和制造误差，以及轴承间隙和高速运转长期使用时的磨损间隙带来的振动、碰撞等，对于由此产生的运动学和动力学影响问题进行分析，求解更符合实际工况的特性分布规律，以指导后续的基于弹性动力学并考虑间隙的高速引纬机构优化设计问题。

1 空间连杆引纬机构结构简介

从运动学角度讲，空间连杆引纬机构包括3个主要的组成部分：空间四杆机构、平面四杆机构、轮系动程放大机构。整个空间连杆引纬机构由曲柄、叉形架、摇臂、连杆、摇杆、扇形齿轮、小齿轮和剑带轮共8个构件组成，如图1所示。整套机构结构简单，工作可靠性较高。

如图1所示当曲柄在所在平面内做圆周运动时，带动叉形架运动，其运动分量作为平面四杆机构的运动输入，利用连杆机构带动摇杆摆动，通过齿轮轮系组成的动程放大系统连接剑带，使剑带作高速往复运动，实现引纬。

2 含间隙铰的等效杆长理论

等效杆长理论[1]主要是以非连续接触模型为理论基础提出的，销轴在轴套内运动时，销轴中心始终在误差圆内运动，如图2所示。

同一批次杆件尺寸误差和原始间隙误差可看成是随机分布[6]的，其中误差圆半径为统计量，各参数关系如图3所示。

图中O为轴套的中心，C为销轴中心，P为杆件另一端铰链接销轴的中点，r为理论杆长，R为等效杆长，由图中的几何关系可得到

(1)

式中Xr、Yr为销轴中心的局域坐标，Xr与PO方向相同为正。一般假设C点总是在误差圆内服从随机分布，这里假设服从正态分布。误差圆半径值G为统计量，则G的均值和方差分别为：

E(G)=[E(d轴套)-E(d销轴)]/2

(2)

D(G)=[D(d轴套)+D(d销轴)]/4

(3)

根据概率论，在±3σ之间置信度达到99.73%[7-8]，则有

(4)

根据方差定义有

(5)

将式(5)代入式(4)得到：

(6)

(7)

根据正态分布的对称性

E(Xr)=E(Yr)=0

(8)

3 空间四杆机构分析

3.1 空间四杆机构运动分析

如图1所示的a部分为空间连杆引纬机构中的空间四杆机构，是典型的主、从动摇臂杆转轴相互垂直的RSSR机构。根据机构中构件的运动关系，得到空间RSSR机构的运动关系简图，如图4所示。

图4中，以曲柄转轴中心O点为坐标原点，竖直向上为Z轴正方向，曲柄转动平面为XOZ平面，摇臂摆动平面为YOZ平面，建立如图OXYZ三维坐标系,其中曲柄OA理想长度为L1，连杆AB理想长度为L2，摇臂BC理想长度为L3，OC理想长度为L4。B、C分别为摇臂与叉形架与机架之间的铰链接，曲柄与X轴正方向的夹角为α1X，摇臂与Y轴正方向的夹角为α3X。

3.2 RSSR机构运动精度分析

以杆AB为例，考虑到空间RSSR机构中的尺寸误差J和因为加工误差或磨损带来的铰间间隙K，一般情况下，假设各输入参数都服从正态分布[9-10]。Ji(i=1,2,3,4,)服从正态分布N(μJi,,σJi)，其中μ=μJ时,杆长取理想长度，则Ji服从正态分布N(0,σJi)。考虑间隙对杆件等效长度的影响，Ki(i=1,4)～N(μKi,,σKi)，分别对应图4中的O、C2个平面铰链接)。

AB两端为空间铰链接，杆长L2在考虑尺寸误差外还应该考虑空间铰间间隙的影响，空间铰间间隙的处理[3]一般将间隙等效到相应的杆长上，假设AB杆两端间隙Ki(i=2,3)分别对应图2中的A、B2个空间铰链接，假设K2、K3分别服从随机分布N(uK2,σK2)、N(uK3,σK3)。

(9)

式中：当AB杆受拉时取+；受压时取-[11]。

将O、C两处的平面铰间间隙等效到OA杆和BC杆上，由式(5)、(6)得各杆件的实际等效长度：

(10)

(11)

(12)

式中L4为机架，考虑安装位置误差，按尺寸误差计算。

3.3 工程分析

假设K1，K4～N(0.2,0.08)，每处平面铰间隙的Xr～N(0,0.07)、Yr～N(0,0.07)、K2，K3～N(0.1,0.05)。根据所研究的空间连杆引纬机构的尺寸和各杆件的运动关系，以MatLab为平台进行编程和仿真分析[12]。相关实际尺寸如表1所示。

表1 RSSR机构参数Tab.1 Parameters of RSSR

曲柄OA的起始角为0°，分别考虑尺寸误差存在、间隙存在和二者综合的情况下，杆BC的运动输出特性曲线如图5～7所示。图中曲线2为理想状态下摇臂的运动特性曲线。

从图5～7中可看出：在所给定数据的情况下，尺寸误差对输出的精度影响略小于间隙的影响；且二者共同作用时对输出精度的影响存在一定的叠加关系，此时摇臂的输出误差可能达到最大。从角位移、角速度和角加速度方面看，在考虑杆长的尺寸公差和磨损和装配带来的间隙的情况下，摇臂的角位移变化不大，角速度曲线出现小幅的波动，而角加速度曲线出现了大幅的波动,如图7(c)，形成了波动幅度很大的锯齿状波形。综合考虑杆件尺寸误差和间隙时，摇臂的输出与理想情况下的偏差如图8 所示。

从图8中可看出，存在尺寸误差和间隙情况下，摇臂的角位移和角速度输出偏差在一个较小的区间波动，而摇臂的角加速度波动十分明显，波动幅度很大。且摇臂的摆角运动输出误差的极值出现在90°、270°附近，此时速度达到最大值，可见在速度的极大值点附近机构的运动输出误差达到最大，而在180°附近，机构的运动输出最小，此时机构的速度和加速度都处于极小值。相比低速情况，机构尺寸误差和机构中的间隙对高速机构的运动输出影响更加明显。

4 平面四杆机构分析

4.1 平面四杆机构运动分析

平面四杆机构是空间连杆引纬机构中的重要部分，其构件的误差直接影响到整个运动的输出，从而导致引纬误差和产品质量的下降。图9示出含间隙平面四杆机构示意图。本文以等效杆长理论为基础，对平面四杆机构进行误差分析。

RSSR机构在YOZ平面的输出量作为平面四杆机构的输入量，连接C点和E点，其中角β和角γ分别为CE杆和BE杆、CE杆和DE杆的夹角，D和E分别为扇形齿轮和连杆、机架之间的铰链接,α5X为扇形齿轮和Y轴之间的夹角。当α3x为已知时，可以求出α5x的变化量，进而得到整个引纬机构的运动输出。

4.2 平面四杆机构精度分析

假设平面四杆机构中，每处平面铰间间隙的Xr～N(0,0.07)、Yr～N(0,0.07)，杆BC、杆CD、杆DE、杆EC的理想长度分别为L3、L5、L6、L7(L7为机架，考虑安装位置误差，作为尺寸误差考虑)。则Ji(i=3,5,6,7)服从正态分布N(0,σJi),在考虑尺寸误差和间隙情况下,各杆的等效长度为：

(13)

各杆长参数如表2所示。

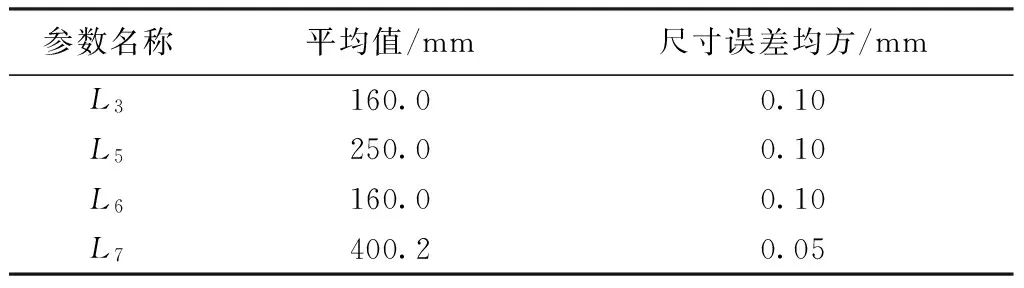
表2 平面四杆机构参数Tab.2 Parameters of planar four bar mechanism

通过空间连杆机构和平面四杆机构的误差累积，通过啮合齿轮的动程放大系统转化成剑头的输出，依据各参数的几何关系，运用MatLab编程，最终得到考虑空间四杆机构和平面四杆机构尺寸误差和铰间间隙情况下剑头的输出特性曲线(见图10)和输出参数的偏差曲线(见图11)。图10中曲线1为各种其他情况下剑头的运动输出曲线，曲线2为理想情况下剑头的运动特性曲线。

从图中可看出：剑头位移偏差在0～4 mm之间变动，变动区间很小；速度偏差在0～3 m/s之间变动，变动幅度不是很大；加速度变动范围很大，波动十分剧烈。且误差极大值出现在速度极大值点附近，在速度和加速度较小的区间，相应的误差输出误差也较小。可见高速场合下，考虑尺寸误差和间隙对机构的运动精度分析是十分必要的。

5 结 语

1) 间隙和尺寸误差给剑头带来的精度影响具有一定的随机性，以等效杆长理论为基础，将间隙等效到对应的杆长上，能够将复杂的间隙问题简单化，具有很高的工程使用价值。

2)在考虑尺寸误差和间隙的情况下，剑头的输出位移变化不大，但是速度和加速度出现一定程度的波动，其中加速度对尺寸误差和间隙非常敏感。

3)空间连杆引纬机构中的RSSR机构和平面四杆机构会出现误差累积，且在高速阶段机构的运动输出较低速阶段大，在高速机构中尽量减小或避免尺寸误差和间隙对保证空间连杆引纬机构的运动输出精度是十分有必要的。

FZXB

[1] LEE S J, GILMORE B J. The determination of the probabilistic properties of velocities and accelerations in kinematics chain with uncertainty[J]. Journal of Mechanisms Transmissions and Automations in Design,1991(113):84-90.

[2] 顾井峰,冯蕴雯，冯云生.任意空间四杆机构运动精度及可靠性分析[J].机械科学与技术,2012(31):814-817. GU Jingfeng, FENG Yunwen, FENG Yunsheng. Analysis of kinetic accuracy and reliability of space four-links mechanism[J]. Mechanical Science and Technology for Aerospace Engineering, 2012(31):814-817.

[3] 吴焕芹,程强，钟诗清.含间隙平面四杆机构运动特性分析[J].武汉理工大学学报,2010(32):419-422. WU Huanqin, CHENG Qiang, ZHONG Shiqing. Analysis of motion characteristics for plane four-bar mechanism with clearance[J]. Journal of Wuhan University of Technology,2010(32):419-422.

[4] 宋月娥,吴林,戴明.机器人关节间隙误差分析[J].机械工程学报，2003(4)：11-16. SONG Yuee, WU Lin, DAI Ming. Error analysis of robot joint clearance[J]. Journal of Mechanical Engineering, 2003(4):11-16.

[5] 邹文韬.含运动副间隙平面连杆机构运动时变可靠性研究[D].成都：西华大学，2013：21-45. ZOU Wentao. Time-dependent reliability analysis of planar linkage mechanism with joint clearance[D]. Chengdu: Xihua University,2013: 21-45.

[6] 黄玮，冯蕴雯，吕震庙，等.考虑铰链运动副间隙的机构可靠性分析模型[J].机械强度，2007,29(2)：264-268. HUANG Wei, FENG Yunwen, LÜ Zhenmiao, et al. Analytical model of mechanism moving reliability taking account of kinematics joint gap [J]. Journal of Mechanical Strength,2007,29(2):264-268 .

[7] 董霞,王恪典.一种间隙副连杆模型及其在复杂机构精度分析中的应用 [J].机械科学与技术，2005(24)：479-484. DONG Xia, WANG Kedian. A lingkage model with revolute clearance and its application to analyzing the precision of a complex linkage [J]. Mechanical Science and Technology for Aerospace Engineering, 2005(24):479-484.

[8] 袁英才,刘义伦,王仪明. 含运动副间隙的轮转机刀式折页机构的动态响应特性[J]. 中南大学学报(自然科学版),2011(42):972-976. YUAN Yingcai, LIU Yilun, WANG Yiming. Nonlinear dynamic response of offset press′s fold mechanism with clearances[J]. Journal of Central South Univer-sity(Science and Technology),2011(42):972-976.

[9] ASOKK Mallik, SANJAYG Dhande. Analysis and synthesis of mechanical error in path-generating linkages using a stochastic approach [J] Mechanism and Machine Theory,1987,22(12):115-123.

[10] BAKER J Eddie. On 5-rovolute linkages with parallel adjacent joint axes[J].Mechanism and Machine Theory, 1995,25(19):467-475..

[11] 华大年，华志宏.连杆机构设计与应用创新[M].北京：机械工业出版社,2008：150-162.

HUA Danian, HUA Zhihong. Design and Application and Innovative of Linkage[ M ]. Beijing: China Machine Press,2008: 150-162.

[12] 郭仁生.机械工程设计分析和Matlab应用[M].2版.北京：机械工业出版社，2008：120-135. GUO Rensheng. Mechanical Engineering Design Analysis and Application of Matlab [M]. 2nd ed.Beijing: Machinery Industry Press，2008:120-135.

Comprehensive analysis of motion accuracy for spatial linkage weft insertion mechanism with clearance and dimensional errors

ZHANG Lei, HE Hu, KONG Jiayuan

(College of Mechanical Engineering & Automation, Zhejiang Sci-Tech University,Hangzhou, Zhejiang 310018, China)

In order to analyze the effect of clearance and dimensional errors of weft insertion motion accuracy, non continual-contacting model and the equivalent length theory are introduced in this article. Considering the manufacturing error and the wear or assembly clearance, kinetic models are established for the spatial four-bar mechanism and the planar four-bar mechanism of the spatial linkage weft insertion mechanism based on the probabilistic analysis method and non-continual contacting theory. The movement simulation is carried out by the calculation and simulation module of MatLab to obtain a related curve. The influence of size error and clearance to the mechanism motion output is analyzed in detail. When considering the component error and clearance between the kinematic pair, the output error of sword head is more obvious than considering a factor only, the maxima error is near the maximum point of the speed, which indicates that the influence of clearance and component error in high-speed mechanism is particularly serious. The results of this study can provide reference for the research of motion accuracy of spatial four bar weft insertion mechanism.

weft insertion mechanism; non continual-contacting model; clearance; equivalent length theory; dimensional error

10.13475/j.fzxb.20150500707

2015-05-06

2015-12-14

国家自然科学基金(51175475)；浙江省自然科学基金(LY14E050027)

张雷(1974—)，男，副教授，博士。主要从事机器人和纺织机械的研究。E-mail：lzhang@zstu.edu.cn。

TS 103. 33

A