ITD改进信号子空间超声检测信号去噪

李大中,赵　杰,刘建屏,蔡文河,马延会（.华北电力大学自动化系，河北　保定07003；.华北电力科学研究院有限责任公司，北京00045）



ITD改进信号子空间超声检测信号去噪

李大中1,赵杰1,刘建屏2,蔡文河2,马延会2
（1.华北电力大学自动化系，河北保定071003；2.华北电力科学研究院有限责任公司，北京100045）

摘要：金属材料超声检测信号中存在的干扰噪声严重影响实际缺陷的检测精度，因此必须对采集的检测信号进行有效去噪处理。针对传统信号子空间去噪方法的不足，提出固有时间尺度分解（ITD）改进信号子空间信号增强算法的超声检测信号去噪方法，融合ITD方法和信号子空间的优势。通过现场超声检测缺陷信号数据的对比验证表明，信噪比、均方根误差和相关性等参数都比较满意，对含有有色噪声的超声检测信号去噪效果明显。

关键词：超声检测；去噪；固有时间尺度分解；信号子空间

0 引　言

信号增强技术作为信号处理的重要分支，被广泛应用于抑制噪声、信号合成与识别领域。在实际现场的超声波金属探伤过程中，由于金属材料的特殊性、探伤设备的自身干扰和实际检测环境的复杂性，超声检测回波难免会有大量噪声信号和固有信号混叠的情况，给超声检测信号后期处理与缺陷识别带来较大困难[1]，因此在对超声信号进行时频域分析之前进行有效的去噪处理很有必要。其中采用相关语音增强算法对带噪超声检测信号进行去噪处理是现阶段超声检测信号研究的最为深入的方法之一，也是可以有效去除噪声干扰的手段之一[2]。信号增强一般属于信号预处理，通过分析不同噪声特性采用不同的信号增强方法，常用的信号增强算法有基于短时谱估计的信号增强算法以及基于信号子空间的信号增强算法。短时谱估计信号增强算法已经在大量文献中得以研究[3]，其算法复杂，增强后的信号仍含有无用噪声，适用的信噪比范围较窄，在去噪过程中容易丢失固有信号中的有用成分，同时会引入较大的噪声。而信号子空间技术可以通过控制无用噪声消除程度及信号失真程度两方面进行去噪，在信号去噪领域得到不断关注，并有较好的去噪效果。

文献[4]将信号子空间技术与端点检测对大地电磁信号进行二次信噪分离处理，有效地补偿了形态滤波处理过程中损失的低频有用信号[4]。文献[5]将信号子空间谱域约束技术应用到图像去噪中，散斑噪声抑制效果明显。虽然信号子空间技术在白噪声环境下去噪效果明显，但是当信号中存在有色噪声时，传统信号子空间技术去噪效果明显下降。白噪声是功率谱密度不变且在整个频域内都均匀分散的随机信号，理想的白噪声在频域内具有无限带宽。因此，实际环境中并不存在完全的白噪声，当实际噪声不具备上述性质时，此时的噪声信号为有色噪声，而粉红噪声（pink noise）是最常见的，常用在声学测试中，不同于白色噪声，粉红噪声的频率分量主要分布在中低频段。

Frei等[6]于2006年提出了一种针对非线性、不平稳信号的新方法-固有时间尺度分解（ITD）。该方法适合分析非线性具有时变谱的不平稳信号，不需要样条插值和筛选过程，因此几乎没有边缘效应，计算速度很快，可以实时处理大量数据。基于此，本文提出一种ITD改进信号子空间技术的去噪方法，并依据现场超声检测缺陷信号数据进行了对比验证，得到了较为满意的结果。

1 信号子空间

信号子空间法在去噪过程中既可以控制信号失真程度，也可以权衡无用噪声的消除程度。

1.1 信号子空间原理

信号子空间技术是将实际中带噪声信号看成由两个向量空间组成，通过将带噪声信号投影到信号子空间和噪声子空间，这里信号子空间主要包括纯净信号成分和很少的噪声成分，将噪声子空间内全部信号置零滤除噪声子空间及信号子空间中的噪声成分，尽可能保留信号部分从而得到近似纯净的信号[7]。

用x表示无任何噪声的纯净信号，n表示加性噪声向量，y表示由纯净信号和加性噪声叠加而成的带噪声信号。假设纯净信号x和无用噪声n互不相关，此时有：

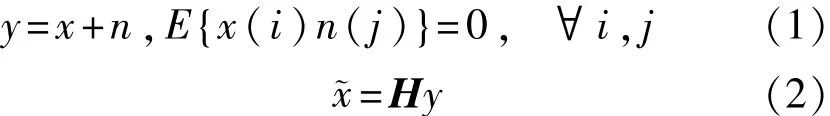
为平衡信号失真量和剩余噪声量，将信号失真能量进行最小化，利用特征值分解[9]（eigenvalue decomposition，EVD）可以得到当噪声为白噪声时，纯净信号x的最优线性估计矩阵如下：

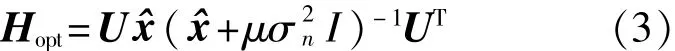
式中：μ——拉格朗日算子[10]；

该估计矩阵是一种次优估计，在白噪声背景下去噪效果明显，但遇到有色噪声时此算法去噪存在明显不足。为弥补该算法对有色噪声去噪效果的不足，通过对矩阵Rx和Rn同时对角化，获得有色噪声背景下的最优估计矩阵如下：

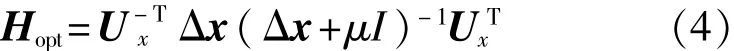
式中Δx与Ux分别为特征值对角矩阵和特征向量矩阵，将式（4）代入式（2），得到原始纯净信号x的最优估计如下：

式中Gμ=Δx（Δx+μI）-1为增益函数。

1.2 超声检测信号子空间去噪

超声缺陷信号去噪试验的主要流程是：选取具有代表性的缺陷，在指定工件上人为制造缺陷，使用信号采集装置收集缺陷的回波信号，在Matlab里进行去噪处理。将信号子空间技术应用到超声检测信号去噪中，具体步骤如下：

1）采集超声缺陷信号。为采集真实的钢材料中超声检测缺陷信号，制作钢材料试块如图1所示。在60 mm×40 mm×30 mm的试块中做直径为5 mm、深10 mm的圆柱形孔。通过超声波发生接收器CTS-8077PR与示波器DPO2012连接，用中心频率为5 MHz、直径为10 mm的直探头采集到此钢材料中缺陷样本信号如图2所示，采样频率为1 GHz，数据长度为3500。

2）获得带噪声信号。通过将原始超声检测信号与白噪声和粉红噪声叠加，获得需要去噪处理的带噪声信号，如图3所示。

3）信号子空间去噪。利用式（5）中原始纯净信号x的最优线性估计，将带噪声信号投影到信号子空间和噪声子空间，通过分帧构造协方差矩阵，对该协方差矩阵进行特征值分解，设置判断阈值将小特征值置零，即可得到全部置零的噪声子空间，重构该帧信号，并使全部帧信号连接起来得到去噪后信号，如图4所示。

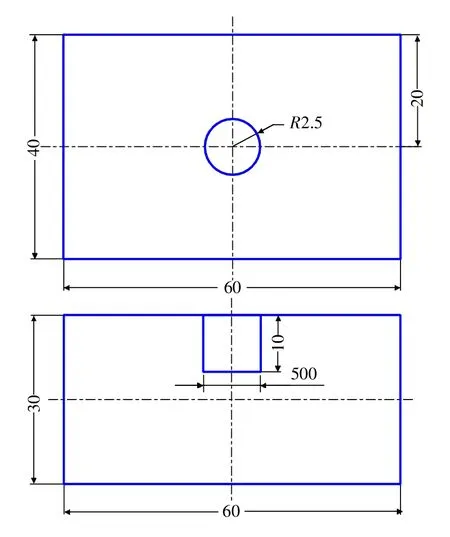
图1 钢材料试块图（单位：mm）

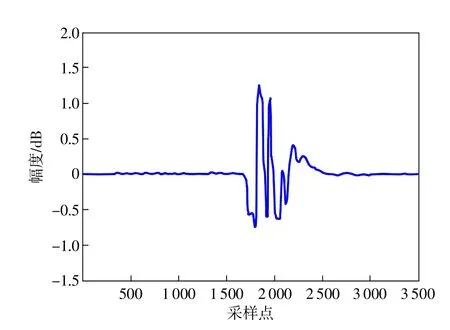
图2 现场原始超声检测缺陷信号

由图可知，利用信号子空间对带白噪声信号与粉红噪声信号进行去噪处理，白噪声信号去噪虽然仍残留一些无用噪声，但整体去噪效果明显，对之后超声检测信号的分析处理影响较小。但该方法对粉红噪声信号去除效果较差，信号严重失真，无法对其进行下一步的信号时频域分析处理。

2 固有时间尺度分解

固有时间尺度分解作为目前最新的信号分解方法，对不平稳信号具有高度的自适应性，该方法将超声检测信号分解成一系列瞬时频率有物理意义的固有旋转分量（PRC）和一个单调的趋势残量之和。得到ITD分解结果后，可以对任意一个固有旋转分量进行频谱分析，从而获得原来信号难以显现的调幅特征和调频特征。

图3 带噪声信号

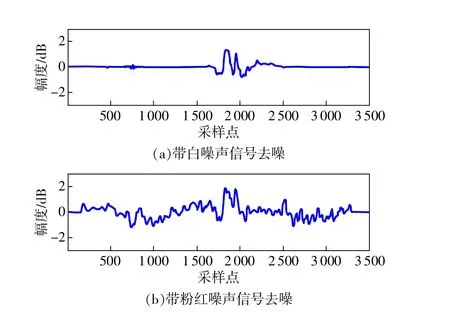
图4 信号子空间去噪结果

假设需要处理的超声检测信号为Xt，是一组由实数构成的离散数据。寻找Xt中的所有极值点，其对应的信号时刻为k（k=1，2，…，M，M为信号极值总数）。首先定义L为基线提取算子，令0=0，则信号Xt的第一次固有时间尺度分解为

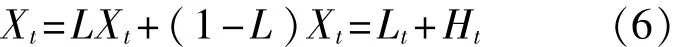
式中Lt=LXt和Ht=（1-L）Xt分别为基线提取信号和固有旋转分量（PRC）。

第一次分解通过从原始超声检测信号Xt中去掉一个基线提取信号得到一个固有旋转分量。之后用Xk和Lk等同于X（k）和L（k），为使Xt在t∈[0，k+2]有意义，定义Lt和Ht都在[0，k]上。在连续极点间隔区间[k k+1]上，定义分段线性基线提取算子[11]如下：

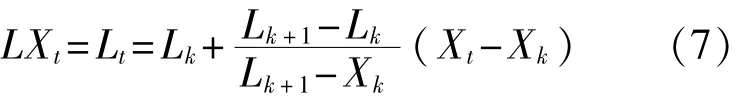
其中

式中σ为用于控制提取固有转动分量幅度的线性缩放，σ∈[0，1]，通常取σ=0.5。

分解出来的固有旋转分量表示原始超声检测信号Xt中的局部相对高频成分，即PRC分量。将基线信号作为下一次的的原始信号继续进行固有时间尺度分解，获得一系列按频率段从高到低不同排列的固有旋转分量，当迭代至产生一个单调的残余趋势信号时分解结束。信号Xt整个固有时间尺度分解过程[12]如下：

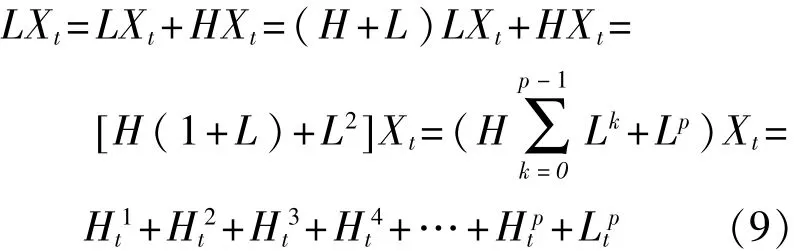
量个数为p。

由于该方法提出时间较短，在信号处理及故障诊断领域应用还很少，但已有文献证明该方法可以对带噪声信号进行比较基础的去噪。因此本文提出ITD方法对信号子空间技术进行改进的信号去噪方法，首先对该带噪声信号进行分解，得到一系列固有旋转分量和残余趋势分量，对其噪声分量进行剔除后重构其余分量可达到一定的去噪效果。

3 ITD改进信号子空间方法

鉴于传统信号子空间技术在对粉红噪声进行去噪时效果差的情况，将ITD方法对信号子空间技术进行改进。

3.1 信号ITD分解

超声检测信号是一种复杂的不平稳、非线性信号，固有时间尺度可以将该带噪声超声检测信号分解成若干个固有旋转分量，如图5所示。获得的瞬时幅值和相位信息能实时反应原始检测信号的特征，相对于其他时频域分析方法更适合分析较大数据量。

由图5可知，带噪声信号经固有时间尺度分解后，得到7个固有旋转分量和1个单调残余分量。其中PRC1，PRC2，…，PRC7为固有旋转分量，r7为单调的残余分量。固有时间尺度分解可以将原始信号分解成一系列较平滑的固有旋转分量，分解后既能反映原始信号的局部细节特征，也没有较大失真。

3.2 ITD改进信号子空间去噪

本文ITD改进信号子空间去噪方法同样利用式（5）对原始纯净信号x进行最优线性估计，将带噪声信号投影到信号子空间和噪声子空间，在分帧后对每帧信号进行固有时间尺度分解，剔除前两阶固有旋转分量（PRC1、PRC2），对其余分量进行重构获得基础去噪后信号，构造协方差矩阵，对该协方差矩阵进行特征值分解，设置判断阈值将小特征值置零，即可得到全部置零的噪声子空间，重构该帧信号，并使全部帧信号连接起来得到去噪后信号，去噪效果如图6所示。

图5 带噪声信号ITD分解

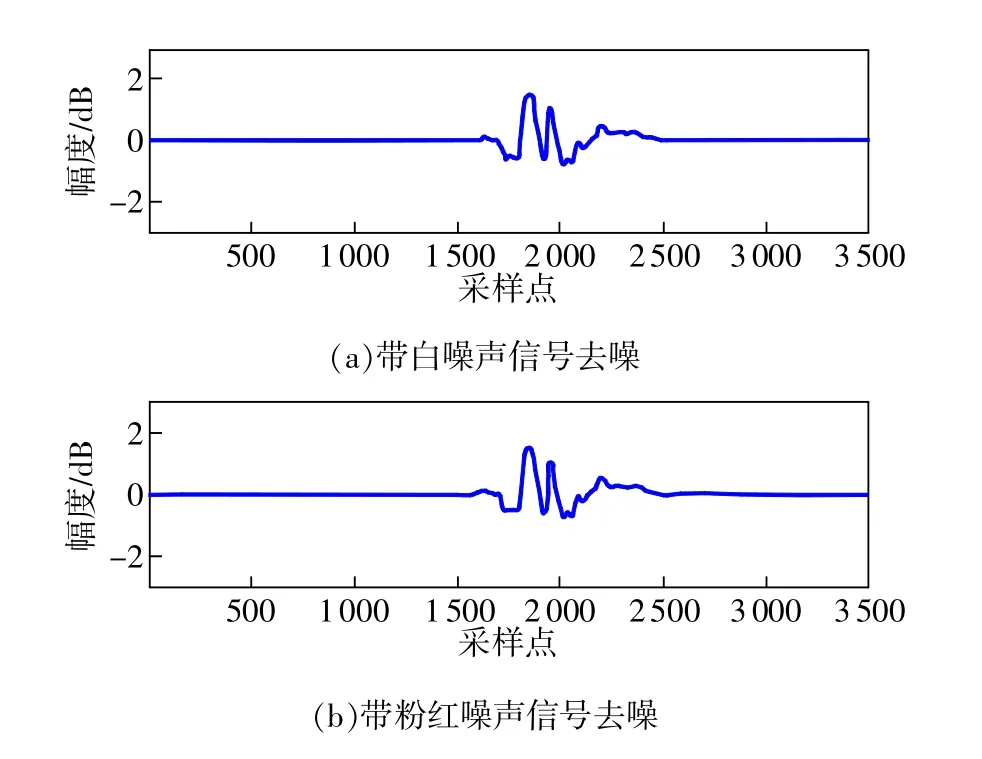
图6 ITD改进信号子空间去噪

由图中ITD改进信号子空间去噪结果，本文方法在白噪声背景下去噪效果与粉红噪声背景下去噪效果都很出色，对比图2中原始采样信号，去噪后信号基本无失真，且去除了大部分噪声。

3.3 去噪效果评价

去噪结果评价一般包括两个方面：主观评价和客观评价。通过对比传统信号子空间和ITD改进信号子空间去噪结果，可以看出后者去噪效果明显优于其他方法。但主观评价由于评价人主观感受的不同而没有确切的判断标准。

去噪效果客观评价一般选用信噪比（SNR）和均方根误差（RMSE）[13]，通过判断原始信号与去噪后信号的接近程度来判断去噪效果，信号越接近，信噪比越大，均方根误差越小，相关系数越大去噪效果越好，将上述方法得到的白噪声和粉红噪声背景下去噪后信号信噪比（SNR）、均方根误差（RMSE）、相关系数（r）分别计算如表1、表2所示。

表1 2种方法白噪声背景去噪效果对比

表2 2种方法粉红噪声背景去噪效果对比

由表可知，在白噪声和粉红噪声背景下，基于ITD改进信号子空间的去噪方法信噪比最大，均方根误差最小，相关系数最大。

4 结束语

本文针对超声检测信号传统信号子空间对有色噪声去噪的不足，提出一种基于ITD改进信号子空间的去噪方法，通过在信号子空间对超声检测信号进行分帧后，对每帧信号进行ITD分解并重构，通过设置判断阈值将噪声子空间置零，在重构每帧信号后并连接起来得到去噪后信号。在白噪声背景和有色噪声背景下本文方法去噪后能够获得最大信噪比以及最小均方根误差。通过现场超声检测缺陷信号数据的对比验证表明，信噪比、均方根误差和相关性等参数都得到了满意的结果，对含有有色噪声的超声检测信号去噪效果明显。

参考文献

[1]李力，余新亮，张全林.超声A扫描信号建模及其缺陷识别方法研究[J].中国测试，2014，40（1）：14-16.

[2]敬人可，李建增，周海林.基于小波包变换和自适应滤波的超声信号去噪[J].中国测试，2014，40（4）：115-118.

[3]刘晓明，班超帆，冯晓荣.失真控制下的短时谱估计语音增强算法[J].西安交通大学学报，2011，45（8）：78-84.

[4]李晋，汤井田，王玲，等.基于信号子空间增强和端点检测的大地电磁噪声压制[J].物理学报，2014，63（1）：019101.

[5]王灿进，孙涛，王锐，等.基于信号子空间谱域约束的激光主动成像散斑噪声去除[J].中国激光，2013，40（11）：217-222.

[6] FREI M G，OSORIO I. Intrinsic time-scale decomposition：time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society of London A，2007，463（2078）：321-342.

[7]曾鸣，杨宇，郑近德，等.μ-SVD降噪算法及其在齿轮故障诊断中的应用[J].机械工程学报，2015，51（3）：95-103.

[8]王玉红，崔波，金梁，等.利用特征极值比的盲信道阶数估计方法[J].信号处理，2015，31（5）：528-535.

[9]王军，闫锋刚，金铭，等.基于噪声子空间映射的二维波达角快速估计算法[J].电子学报，2015，43（2）：276-282.

[10]王楷，宗志亚，孙小惟，等.改进的自适应特征值分解声源定位算法研究[J].仪器仪表学报，2013，34（6）：1241-1246.

[11]黄建才，朱永利.基于改进固有时间尺度分解法的绝缘子泄漏电流去噪研究[J].电工技术学报，2013，28（1）：57-64.

[12]张立国，李盼，李梅梅，等.基于ITD模糊熵和GG聚类的滚动轴承故障诊断[J].仪器仪表学报，2014，35（11）：2624-2632.

[13]刘小春，张蕾.红外图像增强机车电力系统故障诊断与定位[J].中国测试，2014，40（6）：120-123.

（编辑：李刚）

Improved signal subspace method of ultrasonic test signal denoising based on ITD

LI Dazhong1，ZHAO Jie1，LIU Jianping2，CAI Wenhe2，MA Yanhui2
（1. Dept of Automation，North China Electric Power University，Baoding 071003，China；2. North China Electric Power Research Institue Co.，Ltd.，Beijing 100045，China）

Abstract:Interfering noise in ultrasonic testing signals of steel materials has seriously affected the testing precision of actual defects. Therefore，the noise in collected testing signals must be eliminated. A noise -removing method is proposed in this paper to solve the disadvantages of traditional signal subspace based on intrinsic time-scale decomposition（ITD）improved signal subspace. It combines the strengths of the ITD method and the signal subspace. SNR，RMSE and correlation as well as other parameters are satisfactory and the colored noises of ultrasonic defect signals are largely reduced，according to the on-site contrast verification of ultrasonic testing signal data.

Keywords:ultrasonic test；denoising；intrinsic time-scale deposition；signal subspace

文献标志码：A

文章编号：1674-5124（2016）04-0102-05

doi：10.11857/j.issn.1674-5124.2016.04.022

收稿日期：2015-10-20；收到修改稿日期：2015-12-15

作者简介：李大中（1961-），男，内蒙古包头市人，教授，博士，研究方向为新能源发电系统控制、智能优化理论及应用、分布式新能源发电及冷电联产控制系统。