数学教学中开放题的应用

黄敏芝（武夷山旅游职业中专学校，福建 武夷山　354300）



数学教学中开放题的应用

黄敏芝
（武夷山旅游职业中专学校，福建 武夷山354300）

摘要：随着数学素质教育不断深入，开放性问题教学的重要性已越来越被广大数学教师所认识。如何得用现有教材开展开放性问题的教学？是本文所要阐述的主要内容。

关键词：创新；思维发展；认知需求

开放题教学是一种新的数学教学模式，教师必须认识开放题材的作用，根据实际情况利用现有传统题目，开展开放性问题的教学，以适应数学教学的要求。

一、数学开放题的作用

要开展开放性问题的教学，首先要明确开放题的作用：数学开放题有助于增加鼓励和表扬学生机会。有助于开阔学生的视野；学生积极参加学习，发言次数增多，不同层次的学生能做出相应的某种意义的回答；学生增加发现问题和为人所认可的成就感；并可将所学知识综合利用。具体表现在以下几方面：

1.有利于培养学生的创新意识。

由于开放题的答案不唯一，给学生提供了较多提出自己独特的机会，培养学生的创新意识。

2.有利于培养学生良好的思维品质。

由于开放题要求学生寻求条件，结论，寻求不同解法。充分培养学生逆向思维，发散性思维，同时有助于培养学生思维的深刻性，广阔性，创造性，严密性，批判性，进而培养的思维品质。

3.有利于提高学生的主体地位，增强学生学习积极性。

由于开放题有层次性，有利于激发学生的好奇心和求知欲，为学生主动学习创造条件，使用不同层次的学生都能发挥主观能动性，进而达到学有所获的效果。

二、教学实践中开放题的几种开展方法

1.弱化成题的条件，使其结论多样化。

例1.如图1ΔABC是一个钠架，AB=AC，AD是连结A与BC中点D的支架。求证：AD⊥BC（《几何》课本第二册第38页）

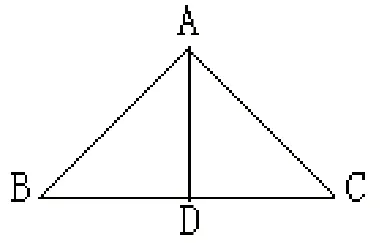
改编为：如图1，△ABC是一个房屋的人字梁，其中AB=AC为了使人字两梁更加稳固，房主要求木工顶点，A和横梁BC之间，加一根柱子AD，你能帮助木工确定D点在BC何处，才能使AD⊥BC吗？

写出方案，，并说明理由.

由于减少D是BC中点条件，便让学生有进行发散性思维的空间.有。有的学生凭直觉大胆猜想D为BC中点；也有学生会根据生活经验，用悬挂重物的方法寻求D点；还有学生想先拉根细线，再用三角板；还有学生说将一矩形长板块靠在A处并使用权矩形较矩边话在横梁上来确定D点。

学生依靠传统命题解题思路，逆向寻找被隐去的条件，唤起他们对问题解决的需要，并且能使学生产生对问题解决思考途径的一种反思。从而加绝对概念本质的理解。

2.隐去成题的结论，使其指向多样性。例2，如图2 ，AB是⊙ο的直径，⊙ο过BC的中点D，DE⊥AC，求证：DE是⊙ο的切线。（《几何》第二册第15页）改编为：如图2，AB是⊙ο的直径，⊙ο过BC中点D，DE⊥AE，垂足为E。

⑴由这些条件，你能推出哪些正确的结论？（要求：不用标注其它字母，如有连辅助线，则应不在结论中出现）

⑵若∠BAC为直角，其它条件不变，除上述结论外，你还能推出哪些新的正确结论？并简要说明理由。

由于隐去原题中结论，使得结论待定化和多样化。这样让学生能充分利用所学有关平行、相似及圆的知识来发现结论，有些甚至会很有新意。

有些问题的答案不确定，解答具有多样性，这决定了它能满足多种层次学生认知需求，有利于学生解答过程中重建认识结构。同时由于综合知识的容量加大，教师可有针对性地把学生分层次地加以引导提高。激发学生学习的好奇心，调动全体学生参加解答过程。

三、将原题特殊化、一般化

例3：求证：等腰三角形底边上任一定点，与两腰的距离和等于腰上的高。

改编为：如图3、在等腰三梯形ABCD中，已知AD∥BC，AB=DC，点P为BC上一点，PE⊥AB，PF⊥CD，BG⊥CD，垂足分别为E、F、G。求证：BE+CF=BG

将原题特殊化，即将等腰三解形变化等腰梯形，其条件，证法相似，便于让学生将知识延伸，达到举一反三的效果。

数学问题的结论往往是在一定条件基础上，由某些特殊条件建构或衍生的特定结果。以现有结论出发，进行联想，探索成立的特殊件，引导学生在求解过程中引出新问题，并将问题加以推广，找出更一般、更概括的结论。

四、开放题应侧重解决问题的思路和策略

学习不应是简单地感知，被动地接受，而需要学生自身积极能动地构造，通过建构，实现主体思维的拓展。通过开放性教学，学生主体精神能更好得以体现，因此应侧重解决问题的思路和策略而不是问题答案，则应注意以下几点。

1.斥其他问题的作用。如培养学生运算能力，使学生会根据法则，公式等正确运算，根据问题条件设计合理，简捷运算途径还得借助传统教学。

2.教师要做好示范。在开放性问题教学中，教师应自觉形成开放的意识，将教学语言演绎得丰富多彩。并处处创设问题的情境，让学生能过动手，动脑，发现规律，找分关系，体验创造性劳动的乐趣，老师在问答过程中起鼓励，指导作用。

3.要注意学生的认识层次，要满足不同学生的需求，对不同思维发展水平学生，应从实际出发，同时，将问题接不同梯度展开，给每个学生有发现的余地，有的放矢地给出一些启发和帮助，从而达到共同提高的目的。必须避免将开放题变成难题，怪题，让学生望而生畏。

综合上述，开放性问题的教学核心是培养学生的创新意思和实践能力。让学生懂得用现代看法解决现代问题仅仅是学习的开始，更重要的是发现新问题，提出新问题，解决新问题，这才是开展开放性问题教学的一种目的所在。

参考文献：

［1］闻黎明“平面几何题改编为开放题的一些做法”《数学教学》。

［2］刘达“由开放性问题设计而产生的开放性问题”《数学教学》。

中图分类号：G633.6

文献标识码：A

文章编号：1671-864X（2016）06-0262-01