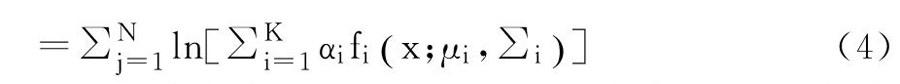基于混合高斯模型的上市企业聚类研究

黄咏宁

摘要：已有的基于上市企业财务指标的聚类研究往往无法反映出聚类过程的不确定性，其聚类结果也欠缺可解释性。在核主成分的基础上，引入了混合高斯模型聚类算法，不仅能较好地实现样本聚类，更能提高聚类结果的可解释性。实验证明以上方法的可行性及有效性。

关键词：财务指标；核主成分；混合高斯模型；聚类

中图分类号：F23 文献标识码：A doi：10.19311/j.cnki.1672-3198.2016.07.046

1 研究背景

上市企业定期公布的财务报表对投资者选股、持股有一定的参考价值，但大量数据背后的信息往往难以被发掘。聚类分析是一种以数据特征为基础的分类技术，通过对上市企业财务数据的聚类分析，能基于财务指标的相似性实现对上市企业的有效分类，对投资者有重要的指导意义。

原思聪（1995）首次探讨了模糊数学方法在股票选择方面的应用，通过综合隶属函数与模糊函数构建了股票选择的评价体系，然而模糊聚类的主观性较强。沈周翔、钟键（2005）则采用主成分（PCA）的方法，通过提取累计方差贡献率大于95%的两个主要成分，将股票财务数据投影到二维平面上，并根据平面象限区分聚类类别，但传统的PCA算法是基于线性组合构造主成分的，并不能处理具有非线性结构的财务数据，因此学者提出了以核主成分（KPCA）技术替代PCA技术进行特征提取。余乐安、汪寿阳（2009）先用KPCA算法对股票的财务数据进行降维处理，再对降维后的数据采用K-Means聚类，这种处理方法能得到准确率更高的聚类结果。但K-Means聚类为硬聚类技术，无法反映KPCA降维及聚类过程中的不确定性，更无法对聚类结果提供有效的解释。针对此问题，在KPCA降维数据的基础上，本文引入一种基于混合高斯模型的聚类算法，能有效地提高聚类结果的可解释性。

2 混合高斯模型软聚类算法

已有研究所采用的聚类算法都是一类优化目标函数的硬聚类算法，其特点是能清晰地对事物进行划分，不允许模棱两可的结果。然而，上市企业的财务指标具有多样性及复杂性等特点，硬聚类算法显然很难基于复杂多样的财务指标将上市企业清晰地加以区分。一种基于混合高斯模型的软聚类算法能有效地解决该类问题。

2.1 混合高斯模型的基本概念

混合高斯模型（Gaussian Mixture Model，GMM）是一种以高斯分布为基础的混合模型，其概率密度函数可表示为多个高斯分布概率密度函数的线性组合。Wilson（1999）已证明，由有限多个高斯分布构成的混合高斯模型能以任意精度逼近任何的多元分布，这种良好的性质使得其在降维或聚类中有良好的应用前景。

2.2 混合高斯模型算法

混合高斯模型是由多个独立的单高斯分布模型（Singal Gaussian Model）的线性组合而成，每一个单高斯分布可称为混合高斯模型的成分（Component）。考虑多元的情况，假设1×d的多维变量x服从单高斯分布，其概率密度函数f（x；μ，∑）为：（1）

其中，μ是1×d的均值向量，∑是d×d的协方差矩阵。而GMM的概率密度函数g（x）则可表示为：（2）

K为成分的数目，在聚类应用中同时代表类簇的数目；α_i（i=1，2，…，K）是权值因子，是第i个单高斯分布在混合模型中所占的权重；μ_i，∑_i分别是第i个单高斯分布的均值向量及协方差矩阵。

2.3 混合高斯模型参数估计

由于聚类是一种无监督学习的方法，其结果具有较强的目的导向性，因此在聚类应用中，聚类类簇数据K，即混合高斯模型的成分个数往往是外生的，而需要估计的参数有α_i、μ_i及∑_i（i=1，2，…，K）。假设N×d的数据集，服从概率密度函数为g（x；θ）的混合高斯分布，θ表示所有参数的集合，其似然函数L的形式如下：（3）

由于单个混合高斯概率密度函数值一般都很小，随着数据点个数N的增大，连乘的结果会变得非常小，容易造成浮点数下溢，因此采用自然对数形式改写目标似然函数：（4）

一般的参数求解方法是通过对对数似然函数求偏导以求得各参数的极值，然而（4）式中在对数函数里面存在大型求和符号，不能用求偏导解方程的发法直接求得参数极值。Bilmes（1998）提出的期望最大化算法（EM），能通过多次迭代的方法简化参数估计过程，进而求取模型参数。

首先初始化混合高斯模型的所有参数，设为θ₀=（α₀，μk₀，∑k₀），k=1，2，…，K，其中K个多元高斯分布的均值向量μk、协方差矩阵∑k可通过统计方法进行计算权值α_i初步设定为1/K。在迭代的过程中，对于第j个样本点x_j，其由第k个多元高斯模型生成的概率定义为：（5）

然后，在第一次更新参数的步骤中，计算可得ω_j1（k），对于任意一个样本点x_j，其值的ω_j1（k）*x_j部分可看作是由第k个单高斯模型产生的，即将该部分数据用作第k个单高斯模型的参数估计。因此，第k个单高斯模型共产生了ω_j1（k）*x_j（j=1，2，…，N）共N个数据点，通过这N个数据点能计算出第k个单高斯模型的均值向量与协方差矩阵参数，在第一次更新参数时，第k个单高斯模型的参数可更新为：（6）（7）（8）（9）

在第一次EM迭代计算后，可得到所有参数的更新值θ₁，用θ₁代替初始化参数，即可以进行第二次的EM迭代计算。在目标精度下，设置一个阈值thresh-old，在n次重复EM迭代后，当满足|ln（L）^[n-1]-ln（L）^[n]|

3 实证分析

3.1 数据来源

本文参考了财务综合能力分析的指标体系构建方法，考虑到数据的全面性及可得性，搜索了2014年沪市、深市134家房地产上市企业的年度财务指标，包括偿债能力、运营能力、盈利能力及发展潜力四个一级维度之下的18个二级财务指标（见表1），形成样本数据集（本文数据来自Wind资讯金融终端，实证分析通过Matlab实现）。

3.2 实证分析

在聚类类簇数目设定上，参考通达信软件对于股票收益率板块的区分（《通达信板块解释》），将作为外生参数设置为三类，分别表示下游企业、中游企业以及优质企业。

通过KPCA降维，在85%的阈值下将18个指标压缩为12个，并以该13412的降维后数据为基础，采用EM算法估算混合高斯模型的参数。参数估计后根据所得的概率矩阵，将134家上市企业聚为三类，其中聚于一类（优质企业）有5家，二类（中游企业）有113家，归于三类（下游企业）的有16家，聚类的三维可视图见图1。其中，132家上市企业能以85%以上的概率进行聚类，说明三成分的混合高斯模型能很好地逼近样本数据的多元分布，对样本聚类的把握性较大，而聚类概率低于85%的两家企业具体情况见表2。从表2可看出，两个聚类异常点与三维可视图结果相似，此外，由于不能以较高的概率确定其归属，因此对该两家企业的聚类情况应谨慎对待。

4 结论及建议

4.1 结论

实证分析显示，基于GMM的聚类算法能较好地实现对房地产上市企业的聚类，并反映各企业归属各类别的概率大小。事实上，GMM参数的估计依赖于样本点属于各个类别的概率大小，当遇到某样本点属于两个类别的概率相差甚小的时候，可对分类结果抱有怀疑态度，从而通过修正算法等方法找寻更精细的分类。

此外，通过GMM参数的估计，能获得各类簇近似的单高斯分布，而通过相应单高斯分布能深入了解到各类簇的结构与性质，便于对各类簇进行评估或进一步的研究。

4.2 建模的启示及建议

综合上述分析，有如下启示和建议：

（1）对于证券公司而言，其公布的业绩评价对于投资者购买股票具有举足轻重的作用，因此其评价必须严谨并有充分的依据。通过本文的分析，券商可以适当在上市公司业绩评级的过程中采用高维数据聚类的方法，通过该方法所得的聚类结果较之传统的净资产收益率识别具有更高的可信性。

（2）对于政府而言，加快证券市场的改革进度，进一步完善上市公司财务报表审核机制，确保所以上市公司公开财务报表的真实性。只有基于准确真实的数据出发，才能使研究结果贴近市场、贴近企业、贴近投资者，才能带动金融行业的进一步发展。

（3）对于科研大部分传统的统计分析手段都可以采用不同方式与大数据结合，并且基于大数据研究基础上的统计分析结果往往由于单纯的传统分析结果，其结论通常更具有针对性、前瞻性，对于丰富统计分析的内容，提高统计分析的质量具有重要意义。