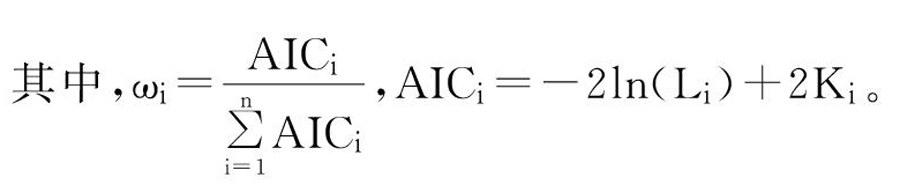我国GDP的组合预测分析

秦雪瑶

摘要：为了更精确的对我国GDP增长状况进行模型拟合与分析预测，采用组合预测的方法，根据模型准则值越小模型越好这一原则，选取若干个准则值较小的模型并赋予不同的权重，组成组合预测模型。并运用软件对我国GDP进行分析得出组合预测模型的预测效果明显优于最优模型的预测效果，预测结果具有更小的误差“风险”的结论。

关键词：模型；GDP；准则；组合预测分析

中图分类号：F2 文献标识码：A doi：10.19311/j.cnki.1672-3198.2016.07.006

1 引言

对我国GDP进行预测分析时，最多的是采取时间序列分析的方法，通过对我国GDP序列进行分析研究，建立合适的ARMA模型，用具体模型对问题的未来发展状况进行预测分析。

建立模型时一般采用AIC准则函数法和BIC准则函数法，选取AIC准则值或BIC准则值最小的ARMA模型作为最优模型，并以此对GDP进行预测分析。但是，在模型的选择过程中，经常会出现几个候选模型的准则值相差非常小的情况。由于用来进行建模的样本观测值都是随机变量，通过样本观测值计算得到的准则值也是随机变量，所以准则值最小的模型并不一定是我们所要寻找的真实模型，其预测效果也不一定比其它模型好。为了解决这个问题提出组合预测模型，并基于组合预测模型对我国的GDP进行预测分析，通过分析发现组合模型的预测效果优于最优模型的预测效果。

2 ARMA模型

ARMA模型的全称是自回归移动平均模型，它对解决我们现实生活中的时间序列问题有非常重要的作用。ARMA模型又包括自回归模型（Auto-regressiveModel，AR）、移动平均模型（Moving Average Model，MA）和自回归移动平均模型（Auto-regression Mov-ing Average Model，ARMA）三大类，主要用于研究零均值的白噪声序列，该模型的一般形式为：

（1）

3 模型建立的步骤

建模的目的是充分利用已有的信息来预测并获取未来信息，就是利用已知数据对事物的未来状况进行预测。建立模型时，首先要找到合适的模型，并确定好模型的阶数。在本文的研究中，采用组合的ARMA模型对数据进行建模，所以要考虑ARMA模型的建立过程：

平稳性检验。首先对数据进行分析，并用单位根（ADF）检验法检验数据是否是零均值的平稳化序列。如果数据平稳，符合模型要求，就可以建立数学模型；如果不平稳，则要将数据平稳化。

模型识别与定阶。通过模型的自相关函数和偏自相关函数确定模型的阶数。如果模型的自相关图和偏自相关图都拖尾，且分别在p步和q步之后偏自相关系数和自相关系数明显趋于零，则可以大体确定p和q的取值范围，再通过AIC准则，选择最优模型。在本文中，采取组合预测的方式，对所选择的多个模型进行组合，得出组合预测模型，因此要先确定n个模型ARMA（p-m1，q-m2）…ARMA（p，q）…ARMA（p+n1，q+n2），这n个模型分别用M₁、M₂…M_n表示，每个模型都要进行识别与定阶。

估计模型参数。如果差分后的数据满足ARMA（p，q）模型，则可以等价的认为原数据满足ARIMA（p，d，q）模型，其中d为差分次数，这时可以利用差分后的数据对ARMA（p，q）模型进行参数估计，包括p，q的估计和参数a.b的估计。

模型有效性检验。检验模型的残差是否是白噪声序列，如果是，则认为模型是合适的；反之，认为模型是不合适的。通常我们也可以检验模型残差序列的相关性，若模型残差序列不相关，则模型是合适的；反之，模型不合适。

建立组合预测模型。对选取的n个模型的AIC准则值取加权平均得到ω₁、ω₂、ω₃…ω_n，作为组合预测模型的权重，最终得到的组合预测模型M为：

M=ω₁M₁+ω₂M₂+…+ω_nM_n（2）

Li为第i个模型的似然函数值，Ki为第i个模型中未知参数的个数。确定出最终的组合预测模型。

4 采用ARMA模型对我国GDP进行组合预测

4.1 资料来源

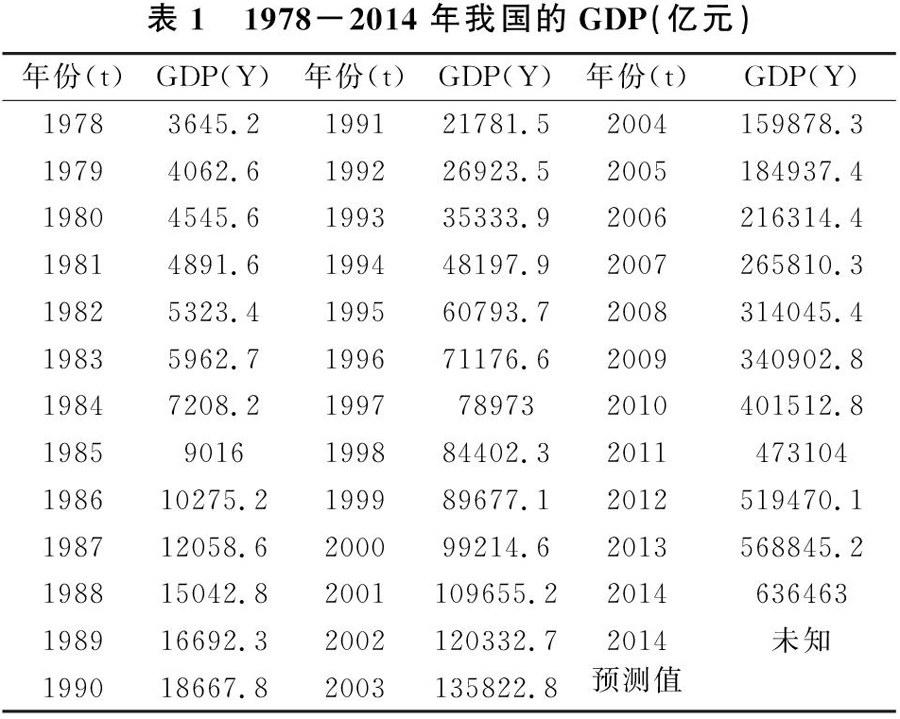
表1是我国1978-2014年的GDP（亿元），来自《中国统计年鉴2014》，选取前36年的数据作为样本数据，基于组合预测分析的方法，运用Eviews软件进行ARMA建模分析，向前一步预测并用2014年的GDP值对模型的预测效果进行检验。

4.2 对我国GDP进行建模

4.2.1 数据分析

根据已知数据，用Eviews软件做出时间序列图（时序图），由时序图可以看出，从1978年至2013年，我国的经济实力不断增强，GDP总量随时间的增长明显增加。

为了使序列变成零均值的线性平稳序列，需要对原序列进行转化。首先对原序列取对数，记H_t=logY_t，由图像可知Y_t为指数趋势序列，则H_t为线性趋势序列。再对H_t进行一阶差分，记为H_t1，消除线性趋势，则H_t1=H_t-H_t-1。

一阶差分后，为了检验H_t1是否平稳，进行ADF检验，检验后得到ADF统计量为-3.568181，大于1%水平下的临界值-3.661661，因此不能拒绝单位根假设，表明经过一阶差分后序列不平稳，故进行二阶差分，记Z_t=H_t1-H_t-11，再对Z_t做ADF检验，如表2。

由表2可知，经检验得到的ADF统计量为-5.270749，小于1%水平下的临界值-3.646342，因此可以拒绝单位根假设，认为序列Z_t平稳，进而可以对Z_t进行ARMA（p，q）模型的相关分析，差分后原数据的模型记为ARIMA（p，d，q），其中d=2。

4.2.2 模型的识别

由模型的自相关和偏自相关图可以得到，模型的自相关函数和偏自相关函数都是拖尾的，可以确定模型为ARMA（p，q）模型，并且在第4期后，偏自相关系数PAC迅速接近0，故p的取值可能是2、3或4，自相关系数AC在第5期后迅速接近0，故q的取值可能是2、3、4或5，因此可能的12个模型分别为：ARMA（2，2）、ARMA（2，3）、ARMA（2，4）、ARMA（2，5）、ARMA（3，2）、ARMA（3，3）、ARMA（3，4）、ARMA（3，5）、AR-MA（4，2）、ARMA（4，3）、ARMA（4，4）、ARMA（4，5）。

4.2.3 模型的选择

对定阶后得到的模型运用AIC准则进行判断，得到各个模型的AIC准则值如表3所示。

按照AIC准则值从小到大排列，候选模型依次为ARMA（2，5）、ARMA（3，5）、ARMA（4，5）、ARMA（4，4）、ARMA（3，3）、ARMA（4，3）、ARMA（3，4）、ARMA（2，4）、ARMA（2，2）、ARMA（2，3）、ARMA（3，2）、ARMA（4，2）。结合参数估计中系数的显著性，最终选取AIC准则值较小的ARMA（2，5）、ARMA（4，4）、ARMA（2，4）三个模型作为真实模型的估计，其中ARMA（2，5）为最优模型。

4.2.4 模型的参数估计

（1）ARMA（2，5）模型的参数估计。

由Eviews软件操作可以得到，ARMA（2，5）模型估计的拟合优度R₂=0.6774，R₂=0.6000，且模型整体上是显著的，其AIC准则值为-3.7452，SC准则值为-3.4246。

然后利用推移算子写出模型ARIMA（2，2，5）的估计结果：

M₁：（1+0.2787B+0.5313B₂）（1-B₂）1nY_t=（1-0.2844B-0.2488B₂+0.2204B₃+01.2532B₄+0.9060B₅）ε_t

（2）ARMA（4，4）模型的参数估计。

同理可得，ARMA（4，4）模型估计的拟合优度R₂=0.6186，R₂=0.4973，且模型整体上是显著的，其AIC准则值为-3.4283，SC准则值为-3.0546。

然后利用推移算子写出模型ARIMA（4，2，4）的估计结果：

M₂：（1-0.6859B+0.1814B₂-0.6276B₃+0.5020B₄）（1-B₂）lnY_t=（1+0.6580B+0.4112B₂+0.7250B₃-0.8268B₄）ε_t

（3）ARMA（2，4）模型的参数估计。

同理可得，ARMA（2，4）模型估计的拟合优度R₂=0.4506，R₂=0.3449，且模型整体上是显著的，其AIC准则值为-3.2752，SC准则值为-3.0003。

然后利用推移算子写出模型ARIMA（2，2，4）的估计结果：

M₃：（1-0.3194B+0.5158B₂）（1-B₂）lnY_t=（1+0.5236B-0.2462B₂-0.0483B₃+0.7246B₄）ε_t

4.2.5 模型的诊断

对ARMA（2，5）、ARMA（4，4）、ARMA（2，4）三个模型进行残差相关性分析，得到三个模型残差序列的样本自相关函数都在95%置信水平内，从滞后1阶至16阶的自相关函数相应的概率值P都远远大于显著性水平0.05，因此不能拒绝原假设，即可以认为三个模型的残差序列不存在自相关，模型是合适的。

4.2.6 模型的组合预测

根据以上分析，可以得出模型ARMA（2，5）、AR-MA（4，4）、ARMA（2，4）都是合适的，都可以用来对我国的GDP进行预测。根据本文提出的方法，将选出的ARMA（2，5）、ARMA（4，4）、ARMA（2，4）三个模型作为模型组，并外推一期，对2014年我国GDP进行预测，然后对模型组采取AIC准则值加权平均的方法进行组合预测，因此组合预测模型为：

M=ω₁M₁+ω₂M₂+ω₃M₃

由上述分析得到三个模型的AIC准则值分别为-3.7452，-3.4283，-3.2752，所以M₁、M₂、M₃模型的权重分别为ω₁=0.3584、ω₂=0.3281、ω₃=0.3135。由此得到组合预测模型M为：

M：（1-0.2253B+0.4116B₂-0.2059B₃+0.1647B₄）（1-B₂）lnY_t=（1+0.2781B-0.0314B₂+0.3017B₃+0.0466B₄+0.3247B₅）ε_t

其中Y_t-1=BY_t。

由表4可以看出，我国2014年的GDP真实值为636463亿元，最优模型及组合预测模型的预测值分别为662012.6亿元、653514.2亿元，预测绝对误差分别为25549.6亿元、17051.2亿元，预测相对误差分别为4.014%、2.679%，组合预测模型的预测值更接近真实值，并且预测的相对误差与绝对误差都小于最优模型，充分说明组合预测模型对我国2014年GDP的预测效果优于AIC准则值最小的最优模型，提高了预测效果，使预测结果更加精准。

5 总结

本文运用组合预测方法，结合AIC模型选择准则，确定合适的权重，构造出组合预测模型。并以1978-2013年我国GDP数据作为样本数据，建立组合预测模型，然后对2014年GDP进行分析预测并与实际值相比较检验预测效果。经过模型检验与实例分析得出组合预测模型在短期预测中的预测效果比AIC准则值最小的最优模型预测效果要好的结论。因此运用组合预测方法，基于1978-2014年数据预测出我国2015年GDP为694645亿元。

从上述实际建模及分析结果可以知道，组合预测模型的绝对误差和相对误差都比单个模型要小，因此组合预测模型与运用AIC准则值最小方法选择的单个模型相比，预测精度有明显提高。组合预测模型综合了各单个模型的优点，充分利用各单个模型所反映的所有有效信息，使预测结果更加接近真实值。

目前，我国经济正处于快速发展的时期，经济态势良好，以组合预测方法，考虑更多影响因素，对经济进行更加精准的预测，有利于为相关决策部门提供更多信息和科学的决策依据，以便制定相关经济政策，调整产业规划，促进我国经济更好的发展。