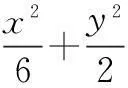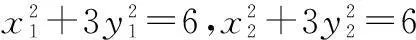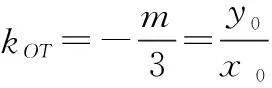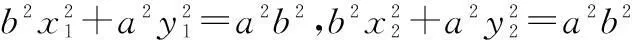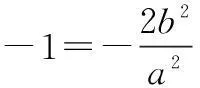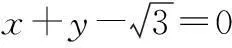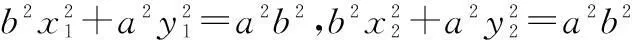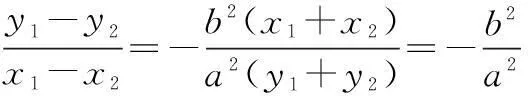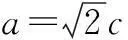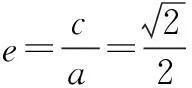例析“点差法”巧解圆锥曲线的中点弦问题
2016-07-08杜彦杰
杜彦杰
(黑龙江省齐齐哈尔市民族中学,161006)
例析“点差法”巧解圆锥曲线的中点弦问题
杜彦杰
(黑龙江省齐齐哈尔市民族中学,161006)
直线与圆锥曲线相交所得中点弦问题,是解析几何的重要内容之一,也是高考中经久不衰的热点.此类问题若用一般解法,不仅过程繁琐,而且运算量大又容易出错,而利用“点差法”解决这类问题,常常能起到化繁为简、出奇制胜的效果.
本文采撷课本和近三年高考试卷中若干中点弦问题,从不同的视角加以审视归纳,分类例说“点差法”在解此类问题中的巧用,希望对大家有所帮助.
一、斜率之积为定值的问题
例1(2015年全国高考题)已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.(1)证明:直线OM的斜率与l的斜率的乘积为定值;(2)略.
证明(1)设A(x1,y1),B(x2,y2),M(x0,y0).由题意,得

∵A,B两点在椭圆上,

两式相减,得
9(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,

∴kAB·kOM=-9,即直线OM的斜率与l的斜率的乘积为定值.
评注题中涉及直线的斜率与弦的中点坐标问题,故可以采取“点差法”.其解题步骤:一是设出弦的两端点坐标;二是代入圆锥曲线方程;三是作差:两式相减,再用平方差公式把上式展开;四是整理:转化为斜率与中点坐标的关系式,然后求解.
二、圆锥曲线上两点关于某直线对称问题
解(1)如图1,设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),则
x1+x2=2x0,y1+y2=2y0.
由题意知,m≠0,
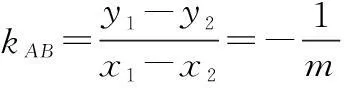
A,B两点在椭圆上,

两式相减,得
(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0,
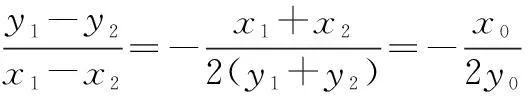

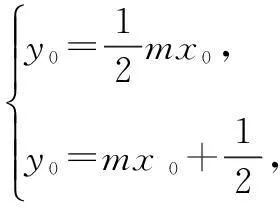


评注圆锥曲线中的对称问题综合性较强,在求解时,应抓住“斜率互为负倒数”与“中点”两个关键点.本题利用“点差法”,求得弦中点的坐标,然后利用中点与椭圆的位置关系(即中点在椭圆内)求解参数的取值范围,简单明了.
三、直线与圆、抛物线位置关系的问题
例3(2015年四川高考题)设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB中点.若这样的直线l恰有4条,则r的取值范围是()
(A)(1,3)(B)(1,4)
(C)(2,3)(D)(2,4)
解显然,当直线l的斜率不存在时,必有两条直线满足题设.
当直线l的斜率存在时,设斜率为k.如图2,设A(x1,y1),B(x2,y2),其中x1≠x2,M(x0,y0),则有
y1+y2=2y0.
∵A,B两点在抛物线上,
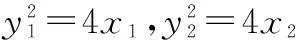
两式相减,得
(y1+y2)(y1-y2)=4(x1-x2),

设圆的圆心为C,由题意知CM⊥AB,

∴x0=3. ∴点M必在直线x=3上.
将x=3代入y2=4x,得y2=12,

又∵点M在圆(x-5)2+y2=r2(r>0)上,


又由题意知,当k存在时,y0≠0,
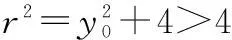
因此有 4 ∴选D. 评注本题意在考查直线与圆及抛物线的位置关系、参数的取值范围等问题.求解时利用“点差法”,求得点M所在的轨迹方程,然后利用点M与圆、抛物线的位置关系,得到r的取值范围,计算量较少.需要注意的是,在利用“点差法”时,要求中点弦的斜率必须存在,因此,首先要根据题意,讨论斜率的存在性;而对于斜率不存在的情况,可由题意直接进行判断得出结论. 四、平分线段问题 (1)求椭圆C的标准方程; (2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.(i)证明:OT平分线段PQ(其中O为坐标原点);(ii)略. (2)(i)证明:如图3,由(1)可得,F的坐标为(-2,0).设T点的坐标为(-3,m),则直线TF的斜率kTF=-m. 当m=0点时,显然OT平分线段PQ; 设P(x1,y1),Q(x2,y2),PQ的中点为M(x0,y0),则 x1+x2=2x0,y1+y2=2y0. ∵P,Q两点在椭圆上, 两式相减,得 (x1+x2)(x1-x2)+3(y1+y2)(y1-y2)=0, 所以点M在直线OT上,因此OT平分线段PQ. 评析此题在标准答案中用的是一般解法,即利用韦达定理并结合中点坐标公式求解,运算量较大,现利用“点差法”求解,大大优化了解题过程. 五、求圆锥曲线方程的问题 (1)求M的方程;(2)略. 解(1)设A(x1,y1),B(x2,y2),P(x0,y0),则 x1+x2=2x0,y1+y2=2y0. ∵A,B两点在椭圆M上, 两式相减,得 b2(x1+x2)(x1-x2)+a2(y1+y2)(y1-y2)=0, ∴a2-b2=3. 因此,a2=6,b2=3, 六、求离心率和的有关问题 解设A(x1,y1),B(x2,y2). ∵M(1,1)是线段AB的中点, ∴x1+x2=2,y1+y2=2. ∵A,B两点在椭圆上, 两式相减,得 b2(x1+x2)(x1-x2)+a2(y1+y2)(y1-y2)=0, 评析本题考查直线与椭圆的位置关系,考查椭圆的简单几何性质,题中涉及弦的中点及其斜率,用“点差法”解决此类问题很方便.