基于弹性地基梁法的沉陷区埋地管道应力变形分析

朱彦鹏,赵忠忠

(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室,甘肃 兰州　730050；2.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州　730050)



基于弹性地基梁法的沉陷区埋地管道应力变形分析

朱彦鹏1,2,赵忠忠1,2

(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室,甘肃 兰州730050；2.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州730050)

摘要场地的不均匀沉降是导致管道破坏的主要原因之一。对沉陷作用下埋地管道进行研究分析,将管道跨越区分为沉陷区和非沉陷区,非沉陷区管道的变形可利用弹性地基梁模型模拟推导出其挠曲线方程,沉陷区管道变形可模拟成三次曲线方程,然后利用边界条件,求得沉陷区管道的内力和位移方程。最后通过实例分析表明:管道的最大应力位于沉陷区与非沉陷区交界面处,且沉陷区管道的最大应力主要由管道内压产生的轴向应力与沉陷作用产生的弯曲应力和轴向应力共同组成,非沉陷区管道主要承受内压产生的轴向应力,故管道内压的影响必须考虑；沉陷量、沉陷区宽度、管径、埋深是影响沉陷区管道变形的主要影响因素,沉陷量、沉陷区宽度的影响最大,而埋深主要影响管道的轴向应力,对弯曲应力基本无影响。

关键词沉陷;埋地管道;弹性地基梁法;挠曲线

埋地管道作为地面工程的重要设施之一,是城市供水、供热、供电、输油、排污的基本组成部分,也是城市的生命线,随着城市化进程的持续发展和城市规模的不断扩大,地下管网的布局越来越复杂,尤其在人口密集的城市地区,大多管道都埋设于建筑物附近,甚至与建筑物地基相邻,一旦发生事故,将会带来重大的经济损失,甚至会造成人员的伤亡。因此,为保证管道的安全运营,对埋地管道的结构性能和设计方法的要求越来越高,而大量地质灾害表明,场地不均匀沉陷是导致管线破坏的最主要原因之一,如震陷、黄土失陷、滑坡、泥石流或其他等原因导致的土体沉降,往往引起管道拉伸或压缩屈曲失稳破坏,不仅带来重大的经济损失,还会带来巨大的社会负面影响[1]。

目前,场地不均匀沉陷下的管道变形研究并不多,而要研究埋地管道的受力变形状况,无论是解析法还是数值模拟法,都要首先研究埋地管道的管土相互作用。对于管土相互作用的研究,Winkler于1867年提出了土介质理想化模型[2],认为土介质表面任一点的位移与作用于该点的应力成正比,将地基模拟成了刚性支座上一系列独立的弹簧,当地面上某点处受到压力时,只有该点产生沉陷位移,而其地方则不产生沉陷,故将这种模型称为局部弹性地基模型。该模型参数单一,计算简便,但没有反应地基变形的连续性,特别是对于密实的厚土层,用该模型分析,将产生较大误差。Newmark等[3]对地下管线进行了振动研究,在分析过程中假定管线与土体一起运动且忽略了惯性力的影响。70年代,日本学者首先提出了管土相互作用理论,主要是基于弹性地基梁模型对地下管道破坏的影响分析,将管道与土之间的相互作用看作是若干弹簧连接来分析地下管道与土介质的相互作用,通过建立管土模型计算管道的应力变形,研究管道在各种荷载作用下的变化规律。1975年,Parmelee等[4]提出了利用半弹性空间中的弹性地基梁模型来分析地下管线与土介质的相互作用。高惠瑛等[5]深入分析了沉陷量、埋深、管径、管土间摩擦系数等多个因素参数对管道的破坏影响。童华等[6]分析了埋地管道在塌陷和冲击作用下管道的大变形。尚尔京等[7]分别采用Winkler模型和理想弹塑地基梁性模型的比较,通过分析计算,得出了管道失效的临界地层塌陷区长度。杨全林等[8]基于地埋管道受力特征的实测结果,建立了地埋管道与土的相互作用分析组合模型,并给出了模型参数的确定方法。基于以上研究理论,在查阅大量相关文献[9,11]的基础上,建立了沉陷作用下埋地管道的分析模型,利用弹性地基梁法对埋地管道进行分析研究,将管道跨越区分为沉陷区和非沉陷区,用弹性地基梁法模拟非沉陷区,求出其管线变形的挠曲线方程,对于沉陷区的变形,参考高惠瑛等[5]用三次曲线方程模拟其结合大变形,并通过沉陷区和非沉陷区交界面处的边界条件及力学协调条件求出的沉陷区管道的位移及内力曲线方程,继而通过实例分析了影响沉陷区埋地管道应力变形的几个因素:沉陷量、管径、沉陷区宽度以及管道埋深,得出了一些建议及结论,为沉陷区埋地管道的分析提供一定的理论基础。

1弹性地基梁分析模型

埋地管道在遭到地层沉陷后,受上覆土体、管内液体以及管道自重的作用,沉陷区会发生较大的变形,利用弹性地基梁法建立模型,将管道看作弹性地基梁,支撑管道的下部土体看成具有一定刚度系数的弹性土弹簧,管道上部的土壤作用表现为主动土压力,简化为作用在管道上的均布荷载,管道下部的土壤作用表现为被动土压力,看做弹性地基,用弹性地基系数k表示,如图1所示。将管道跨越区分为沉陷区和非沉陷区,A点为沉陷区与非沉陷区的交接点,由于非沉陷区管道处于弹性反应状态,故可看作半无限弹性地基梁,假设在沉陷区管道发生了较大的几何变形,且沉陷区发生的最大位移ymax,沉陷区宽度为W,在B′点发生最大位移,利用弹性地基梁的方法分析管道在沉陷作用下管道的强度、变形作用。

1.1非沉陷区管道分析

设非沉陷区的管道满足弹性地基梁模型且忽略惯性力的影响,图1给出了沉陷作用下管道的变形分析模型,管道的弹性模量为E,截面惯性矩为I,上部作用的荷载集度为q(x),土壤刚度系数为K,假定在荷载作用下梁的挠曲线为y=f(x),则梁分布荷载的总集度为

q0(x)=q(x)-Ky。

(1)

荷载、位移以及内力之间的微分方程为

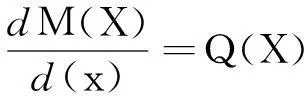
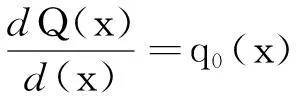
EIy″=-M(x),

其中:M(x)为梁的弯矩；Q(x)为梁的剪力,由此可得

EIy(4)+Ky=q(x)。

(1)

该微分方程对应的齐次性微分方程的通解为

y=eλx(C1cosλo+C2sinλi)+

e-λx(C3cosλo+C4sinλi),

(2)

根据边界条件:x→∞时,y→0；在A点,x=0时,y=0以及MA(x)=-EIy″,求得

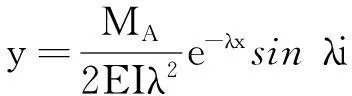
(3)

由式(1)可以看出,其特解就是仅外荷载作用下引起的梁挠度的附加项,所以梁总的挠度值为

y=eλx(C1cosλo+C2sinλi)+

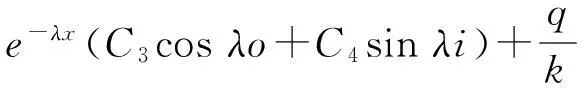
(4)

式(4)为非沉陷区埋地管道的挠曲线方程,C1、C2、C3、C4可根据边界条件求得。

1.2沉陷区管道分析

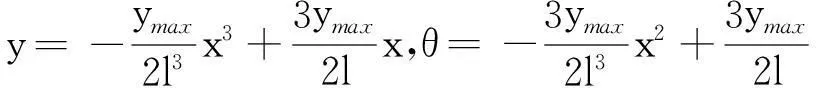
(5)

将管子分成n段,通过受力平衡方程最终解得管道在A点处的弯矩、轴力方程为[3]

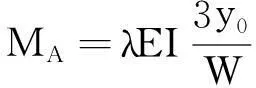
(6)

NA=EA(AC-h)/h,

(7)

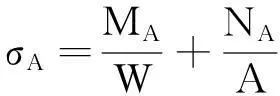
(8)

其中:y0为最大沉陷量；W为沉陷区宽度；h为坐标上的步长；AC为在步长h上的管轴的曲线弧长。

内压引起的管道轴向应力,参照《输气管道设计规范》[11]可得

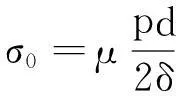
(9)

其中:μ为泊松比；p为管道设计内压力(MPa)；d为管道内径(mm)；δ为管道壁厚(mm)。

故管道的最大应力为

σmax=σA+σ0。

(10)

1.3荷载分析

作用在埋地管道上的荷载,主要有管顶土体的主动土压力、管道自重、管内天然气自重以及内压、管底土体的被动土抗力以及管土之间的滑动摩擦力的共同作用。

上覆土的平均土压力为

q1=0.5(1+K0)γZD,

(11)

其中:γ为土容重；Z为管线埋深；D为管道外径；K0为土压力系数,对于粘性土,该处取0.65。

管道自重为

(12)

其中:ρ为管道容重；r为管道外径；r0为管道外径。

天然气的自重为

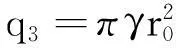
(13)

其中:γ为天然气容重；r0为管道内径。

所以管道受到的均布力为

q=q1+q2+q3,

土体滑动摩擦力为

fp=Pptanφ,

(14)

其中:φ为管土摩擦角；Pp为被动土抗力。

2算例及结果

选取管材为X70的钢,管径为1 016 mm,密度为7 850 kg/m3,壁厚20 mm,屈服强度为485 MPa,管土摩擦角20°,土壤类型为黄土,容重为25kN/m3,泊松比为0.3,管道埋深1.5 m,管道内压力为10 MPa,管道弹性模量E=210 000 N/mm2,截面惯性矩I=0.007 76 m4,λ=0.332 8 m-1,单位长度上管道所受总应力=上覆土压力+管道自重+天然气自重=7.6×104N/m,其下地基的抗压刚度系数为80 MN/m3。对于沉陷区埋地管道的应力分析,主要是研究影响管道受力变形的各影响因素与管道最大应力的关系,而管道最大应力位于沉陷区与非沉陷区交界处,即A点处,该处管道最大应力由管道内压所产生的轴向应力和沉陷作用所产生的管道弯曲应力、轴向拉应力组合而成。选取表1中的参数为分析参数,设定管道最大沉降量、沉陷长度、管径、埋深其中之一为分析变量,而其他参数保持不变,分析管道A点处最大应力随各分析变量变化规律。

根据前面分析过程,利用式(6)～式(8)可得到A点处管道管道的应力值,利用式(9)算得管道的内压,利用式(10)算得管道的最大应力值(A点处),得到以下结果。

图2为沉陷区宽度为30 m时的沉陷量随最大应力变化的曲线。由图2可知,随着沉陷深度的增大,管道最大应力也随着增大。由于X70钢管的屈服强度为485 MPa,故沉陷量超过某一值时,管道的所承受的最大应力值达到管道屈服强度值,管道将发生变形破坏。

图3为沉陷量为0.3 m所对应的沉陷宽度与最大应力曲线图。管道的最大应力随着管道沉陷区宽度的增加而减小,当沉陷区宽度大于70 m左右时,管道处于安全状态。

图4为沉陷量等于0.3 m,沉陷区宽度等于30 m时的管径与最大应力曲线图。管道的最大应力随着管径增大的幅度较小,且增大幅度呈逐渐较小的趋势。此时管道所承受的最大应力已超过管道的屈服强度,管道可能将变形破坏。

图5为埋深对管道轴向应力的影响曲线图。随埋置深度的增加,管道轴向应力逐渐减小,这是由于管道埋深的增加减小了管道的轴向变形。

根据以上分析结果可知,为保证管道的安全运行且管道最大应力不宜超过管道的屈服应力,不同的沉陷区宽度对应不同的最大的沉陷量,表2列出了沉陷区宽度从30～130 m不同沉陷区宽度所对应的允许最大沉陷量。从表2可看出,允许最大沉降量随沉陷区宽度的增加呈线性增长。

3结论

(1) 管道变形最大应力位于沉陷区与非沉陷区交界处,最大应力值是沉陷作用引起的弯曲应力、轴向应力以及管道内压产生的轴向应力的组合值；A点弯曲应力、轴应力值随沉陷量、管径的增大而增大,随沉陷区宽度的增加而减小,而埋深对管道轴向应力的影响较大。

(2) 沉陷作用下的埋地管道,非沉陷区主要承受管道内压产生的轴向应力,沉陷区管道承受的应力主要由管道内压产生的轴向应力与沉陷作用产生的弯曲应力和轴向应力共同组成。管道内压对管道的最大应力值有较大的影响,由于管道周围土体对其具有很大的约束,故内压对管道径向的影响可以忽略,而由于内压引起的管道轴向应力较大,必须予以考虑。

(3) 影响沉陷作用下管道变形破坏主要因素有沉陷量、沉陷宽度管径以及埋深,且沉降量和沉陷深度对管道的最大应力影响最大,其次是管径和埋深,埋深对管道轴应力的影响随其埋置深度的增加呈逐渐减小的趋势,而对弯曲应力基本无影响；因此在不同的地下环境中,为保证管道经济、安全运行,应合理的选取管道截面尺寸以及适当的管道埋深。

参考文献:

[1]焦赘,叶伟林.兰州地区黄土湿陷地质灾害危险性分析[J].甘肃科学学报,2008,20(3):60-63.

[2]龙驭球.弹性地基梁的计算[M].北京:人民教育出版社,1981.

[3]Newmark N M,Hall W J.Pipeline Design to Resist Large Fault Displacement[J].Earthquake Engineering Res Inst,1975:416-425.

[4]Parmelee R A,Ludtka C A.Seismic Soil-structure Interaction of Buried Pipeline[C]//Proc of US National Conf Earthq Eng,Oakland:EERI,1975.

[5]高惠瑛,冯启民.场地沉陷埋地管道反应分析方法[J].地震工程与工程振动,1997,17(1):68-75.

[6]童华,祝效华,练章华,等.坍塌和冲沟作用下埋地管道大变形分析[J].石油机械,2007,35(11):29-32.

[7]尚尔京,于永南.地层塌陷区段埋地管道变形与应力分析[J].西安石油大学学报:自然科学版,2009,24(4):46-49.

[8]刘全林,杨敏.埋地管与土相互作用分析模型及其参数确定[J].岩土力学,2004,25(5):728-731.

[9]罗金恒,赵新伟,王峰会,等.地质灾害下悬空管道的应力分析及计算[J].压力容器,2006,23(6):23-26.

[10]唐永进.压力管道应力分析[M].北京:中国石化出版社,2003.

[11]中华人民共和国建设部,中华人民共和国国家质量监督检验检疫总局.GB 50251—2003输气管道工程设计规范[S].北京:中国计划出版社,2003.

Stress and Deformation Analysis of Buried Pipelines on Subsidence Area by Base Beam Method of Elastic Foundation

Zhu Yanpeng1,2,Zhao Zhongzhong1,2

(1.Key Laboratory of Disaster Prevention and Mitigation in Civil Engineering of Gansu Province,Lanzhou University of Techonology,Lanzhou 730050,China;2.Western Center of Disaster Mitigation in Civel Engineering of Ministry of Education,Lanzhou 730050,China)

Key wordsSettlement;Burial pipelines;Base beam method of elastic foundation;Deflection curve

AbstractThe differential settlement of ground is one of the main reasons which causes pipeline damages.The research and analysis on buried pipelines under effect of settlement usually divide the pipeline crossing area into subsidence area and non-subsidence area.Deflection curve equation of deformation of pipelines in non-subsidence area can be simulated and deduced by using base beam model of elastic foundation.Pipeline deformation on subsidence area can be stimulated into cubic curve equation,and then concluded internal force and displacement equation of pipeline on subsidence area by using boundary conditions.The conclusions after combining living examples and analysis indicate that maximum stress of pipelines locates on the interface between subsidence area and non-subsidence area.Maximum stress of pipeline on subsidence area is jointly constituted by axial stress caused by pipeline internal pressure,bending stress and axial stress caused by effect of settlement.As pipeline of non-subsidence area mainly suffers axial stress caused by internal pressure,the effect of internal pressure shall be taken into consideration.The principle influence factors that affect pipeline deformation on subsidence area are settlement volume,width of subsidence area,pipeline diameter and burial depth,among which settlement volume and width of subsidence area have the biggest influence,and burial depth mainly affects axial stress of pipeline,which nearly has no influence on blending stress.

doi:10.16468/j.cnki.issn1004-0366.2016.03.015.

收稿日期:2015-01-15;修回日期:2015-03-09.

基金项目:教育部创新团队支持计划项目(2013IRT13068).

作者简介:朱彦鹏(1960-)，男，甘肃庆阳人，教授，博士生导师，研究方向为支挡结构的设计.E-mail:zhuyp@lut.cn.

中图分类号:TE973.1

文献标志码:A

文章编号:1004-0366(2016)03-0072-05

引用格式:Zhu Yanpeng,Zhao Zhongzhong.Stress and Deformation Analysis of Buried Pipelines on Subsidence Area by Base Beam Method of Elastic Foundation[J].Journal of Gansu Sciences,2016,28(3):72-76.[朱彦鹏,赵忠忠.基于弹性地基梁法的沉陷区埋地管道应力变形分析[J].甘肃科学学报,2016,28(3):72-76.]