空调系统的一种集总参数模型

褚　睿,杨渊晋,王良璧

(1.兰州交通大学 机电工程学院,甘肃 兰州　730070;2.兰州交通大学 铁道车辆热工教育部重点实验室,甘肃 兰州　730070)



空调系统的一种集总参数模型

褚睿1,2,杨渊晋1,2,王良璧1,2

(1.兰州交通大学 机电工程学院,甘肃 兰州730070;2.兰州交通大学 铁道车辆热工教育部重点实验室,甘肃 兰州730070)

摘要空调系统模型的研究对改善系统性能有重要意义。建立的一种集总参数法热力学模型与现有空调系统模型相比,不需要对空调内部各个部件分别建模计算,达到平衡,再进行系统平衡计算,而是选出各个部件模型中与系统模拟密切相关的热力参数,建立其模型,然后直接对所有未知变量同时迭代求解。建立的集总参数法热力学模型具有物理概念清晰、计算过程简明科学、迭代次数少、速度快等优点。

关键词空调系统;系统建模;模拟;集总参数法

我国建筑能耗已超过全国能源消费总量的1/4,空调系统的能耗占总建筑能耗的一半以上[1],对空调系统的研究成为热点问题之一。Hiller等[2]建立了可变容量的空调制冷系统稳态数学模型,对蒸发器、冷凝器采用集总参数建模方法分段建模,计算不同稳态运行工况下的系统性能。Sami等[3]采用集总参数法建立冷凝器、压缩机等部件的动态模型,并且利用流动模型建立换热器的数学模型,给出各区的质量与能量交换关系。在前人的研究基础上,Hamilton等[4]通过编制模拟程序,对制冷系统仿真进行了研究。Chen等[5]采用瞬态和分布参数方法描述独立部件的数学模型,优化部件间的匹配,通过与实验数据对比,分析理论模型的可靠性。Geoffrey等[6]运用稳态数值模拟方法模拟两种混合制冷剂的空调系统,并且通过对一个给定的空调工况和指定的混合制冷剂,程序预测系统(COP,coefficient of performance),结合相关温度、压力和流量,确定压缩机的尺寸和所需的蒸发器、冷凝器。丁国良等[7]提出动态仿真模型,建立压缩机模型、高压侧模型、低压侧模型和毛细管模型,然后分别建立四个有关制冷剂质量流量的方程,对空调器的实际动态工作过程进行仿真。朱瑞琪等[8]以制冷系统控制为目标,建立制冷系统的多输入多输出模型,通过线性化和降阶对系统动态特性12阶非线性微分方程进行模拟计算。杨志刚[9]、王婷等[10]、张飞翔[11]以制冷循环为研究对象,建立空调各个部件的数学模型,各部件分别封闭,计算出一个或几个参数,如冷凝器建立能量守恒的两个方程,计算制冷剂、空气的出口温度,然后局部耦合时修正温度参数,再实现系统的平衡,为制冷系统的多变量联合控制和系统性能的优化提供参考依据。Shao等[12]提出一种新的混合空调系统稳态建模方法,系统的物理模型完全或部分由神经网络取代,相同的计算条件下,偏差的关键性能指标下降±5%,速度是原来的50～100倍。但是在数据库、建模、避免风险方面存在不足。

现有空调系统模型存在很大不足。现有的模型大部分需要将制冷四大部件分别独立建模,模型内部首先迭代平衡,根据系统输入输出的相关性,部件模型之间通过调整热力参数,如蒸发温度、过热度,循环迭代,使假设值和计算值相等,并且使压缩机的质量流量和节流阀的质量流量相等,系统整体平衡。计算过程中,迭代次数较多,而且有时还不能得到预期的结果。

针对现有模型的缺点,以整个空调系统为单一系统,建立该系统的稳态集总参数模型。在此基础上寻求最适合求解系统模型方程的数值方法,并对新模型获得的结果和旧模型结果进行比较分析。

1空调系统的热力学模型

1.1空调系统工质状态的主要参数

空调制冷系统包括压缩机、冷凝器、节流阀、蒸发器四大部件。稳态集中参数法模型中,空调系统各部件的制冷剂质量流量和制冷剂的充灌量基本保持不变,制冷剂的状态确定。系统热力学过程如图1所示。图1中点1为工质进入压缩机的状态,点2为工质出压缩机及进冷凝器的状态,点3为工质进膨胀阀及出冷凝器的状态,点4为工质出膨胀阀及进蒸发器的状态。

整个热力过程共有12个状态参数,如表1所列。

当工质处于完全气态时,p、v、T应满足理想气体的状态方程为

pv=RT,

(1)

这里R为气体常数。根据图1 工质在点1和点2时处于完全气态,从而 p1、v1、T1中只有两个独立变量,p2、v2、T2中也只有两个独立变量。图1中工质在点3时是完全液态,根据工质在液态时的状态方程,可建立p3、v3、T3之间的关系式,从而p3、v3、T3中只有两个独立变量。图1中工质在点4时处在汽液混合的饱和状态,饱和温度和饱和压力之间的关系为

T4=f(p4)。

(2)

工质汽液相的质量比例通过引进干度系数x来表示。即使分别对于汽相和液相,p4、v4、T4只有1个独立变量,但x的引入使得描述点4的独立状态参数为2个。这样一来,图1所示热力学过程中描述工质状态的独立参数还有8个。为了进一步减少描述工质状态的独立参数个数,引入工质流经蒸发器和冷凝器的压力损失分别为△pevap、△pcond,p3与p2及p1与p4之间有如下关系:

p3=p2-Δpcond,p1=p4-Δpevap,

(3)

当△pcond、△pevap为已知时,描述工质状态的独立参数还有6个。

1.2建立模型的假设

为了进一步简化空调系统的热力学模型,需对空调系统的工作状态做如下假设:

(1)在所研究工况下空调系统稳定运行,蒸发器风扇、冷凝器风扇、压缩机的运行参数不随时间变化;

(2)工质压缩过程为多变过程;

(3)工质在膨胀阀进行绝热膨胀;

(4)冷凝器和蒸发器的K值按逆流对数温差整理。

1.3描述空调系统的控制方程

工质在膨胀阀中的焓值满足能量守恒定律

h3=h4,

(4)

压缩机提供的工质质量流量为

(5)

工质在压缩机中的热力学方程为

(6)

工质流经节流阀的质量流量为

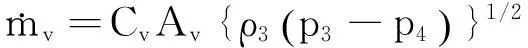
(7)

系统中的传热及能量守恒关系为

Qevap=(KF)evapΔtmevap,

(8)

Qevap+Pin=(KF)condΔtmcond,

(9)

(10)

系统中工质的质量流量应满足质量守恒定律

(11)

1.4描述方程中的参数表达式

蒸发器及冷凝器平均温差分别为

(12)

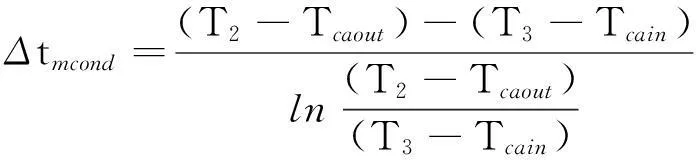
(13)

其中:Teain、Teaout分别为蒸发器空气侧进、出口温度;Tcain、Tcaout分别为冷凝器空气侧进、出口温度。

节流阀流量系数Cv[13]为

(14)

压缩机的理论容积输气量为

Vth=60nπR2Lε(2-ε)/3 600,

(15)

其中:R是压缩机气缸内半径;L是气缸轴向长度;ε是相对偏心值。

压缩机输气系数为

λ=λvλpλTλlλh,

(16)

其中:压力系数λp与回流系数λh为1;泄漏系数λl=0.85;容积系数λv=1-c{(p2/p1)1/m-1},通常压缩机的相对余隙c值一般为1.5%～6%[14];温度系数λT=ATc+B(T1-Te),A=2.57×10-3,B=1.06×10-3,T1是压缩机吸气温度,Te是蒸发温度,即蒸发器出口压力对应的饱和温度,Tc是冷凝器进口压力对应的饱和温度[15],适用于303 K≤Tc≤323 K[16]。

压缩机注入工质的热量Pin为

(17)

工质在点4的干度x为

x=(h4-h4f)/(h4g-h4f),

(18)

(19)

其中:下标f、g分别指饱和液体和饱和气体。

(20)

CVAV{ρ3(p2-Δpcond-p1-Δpevap)}0.5=0,

(21)

(22)

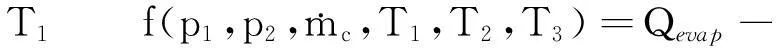
(KF)evapΔtmevap=0,

(23)

Pin-(KF)condΔtmcond=0,

(24)

Qevap-Pin=0。

(25)

2数值方法

空调系统的集中参数法热力学模型,即方程(6)～方程(11)中共有6个未知量。可采用高斯-牛顿迭代法来求解。高斯-牛顿迭代法的基本思想是用泰勒级数展开式近似地代替非线性方程,然后通过多次迭代,多次修正方程组的近似解,使方程组的近似解不断逼近准确值,最后使残差平方和达到最小。

3算例描述

采用的设备有制冷剂R134a、滚动转子式压缩机、电子膨胀阀、换热器。工作参数:额定制冷量为3 100 W的压缩机,转速为2 980 r/min;电子膨胀阀制冷剂流通面积0.5×10-6m2;冷凝器中空气侧进口温度为35 ℃,含湿量为11.2 g/kg,相对湿度为30%,空气质量流量为2 226.24 m3/h,(KF)cond为504.31 W/K;蒸发器中空气侧进口温度为27 ℃,含湿量为11.1 g/kg,相对湿度为50%,空气质量流量为963.06 m3/h,(KF)evap为273.105 W/K。

4计算结果与分析

4.1计算获得的算例额定点参数

4.2与现有系统模型对比

图2是6个状态点在压焓图中的状态位置。图3～图8为集总参数法模型和现有模型的计算结果。空调系统热力过程中6个状态点的热力参数的对比曲线见图3,从图3可以明显看出,各参数的符合度非常好。其中点2、点3处的压力值有一些区别,这是由于研究中的模型和现有模型算出的冷凝温度相差2 ℃,所以计算出的其他参数值会不同,压力误差为3.78%。

4.3空调系统运行参数对其性能的影响

用集总参数法模型与现有模型进行空调运行参数对其性能的影响分析。先考察电子膨胀阀流通面积对性能的影响,得到在额定点能效比最大时所对应的电子膨胀阀流通截面积,在分析压缩机转速、制冷量、室内环境温度、室外环境温度对系统性能影响时均采用此流通截面积。

(1)膨胀阀流通面积当其他参数保持在额定点不变时,电子膨胀阀的流通截面积对系统性能的影响如图4所示。由图4(a)可以看出,随着电子膨胀阀流通截面积的增加,压缩机的进口温度T1基本不变,压缩机的出口温度T2迅速减小,冷凝器出口温度T3基本不变,蒸发器的进口温度T4逐渐减小;由图4(b)可以看出,压缩机的进口压力p1、蒸发器的进口压力p4在缓慢减小,压缩机的出口压力p2、冷凝器的出口压力p3迅速减小,这是因为电子膨胀阀的面积增大,流入蒸发器的制冷剂流量缓慢增加,如图4(c)所示;空调系统的能效比也在迅速增加,当面积增加到0.54 mm2时,系统的能效比相对最大,如图4(d)所示。因此,在之后的研究中流通截面积取Av=0.54 mm2,调整电子膨胀阀的流通面积,可在一定程度上提高空调系统能效比。结果表明,研究中的模型与现有模型的结果近似,所以集总参数模型有很好的适用性,而且计算精确度也很高。

(2)压缩机转速随着压缩机转速的增加,压缩机单位时间输送制冷剂的能力增强,即从蒸发器吸走的制冷剂增加,流入冷凝器的制冷剂增加,冷凝器的热负荷增加。性能参数随压缩机转速的变化曲线如图5所示。由图5(a)可以看出,温度值T1迅速减小、T2迅速减小又出现小幅的增加、T3基本不变、T4迅速增加;由图5(b)可以看出,压力值p1/p4缓慢增加、p2/p3迅速增加;由图5(c)可以看出,制冷剂的流量迅速增加;由图5(d)可以看出,空调系统的能效比先增加后减小,在n<3 220 r/min时迅速增加,n>3 220 r/min后迅速减小,在n=3 220 r/min时能效比达到最大。这是因为在转速变化的范围内,当n=3 220 r/min时压缩机单位时间的实际输气量最大,其能效比最大。因此,对于额定点,持续增加压缩机的转速,并不能达到提高其能效比的目的。

(3)制冷量额定制冷量的研究范围是2 300～3 100 W,再增大时,T2值会超过Tc=101.1 ℃,不满足实际情况,故在此范围内进行计算。性能参数随制冷量的变化曲线见图6。由图6(a)可以看出,随着制冷量的增加,温度值T1缓慢减小,T2迅速增加,当Q>3 000 W时温度出现大幅的增加,T3缓慢减小,T4迅速减小;由图6(b)可以看出,压力值p1/p4缓慢减小、p2/p3缓慢减小;由图6(c)可以看出,制冷剂的流量缓慢增加;由图6(d)可以看出,空调系统的能效比在Q<3 000 W时迅速增加,在Q>3 000 W时迅速减小,因此,Q=3 000 W时能效比取得最大值。制冷量的增加不是越大越对系统有利,而是制冷量要与系统相匹配,它对系统的影响不容小觑。两种模型的计算结果中,p2/p3的计算结果误差较大,平均误差为15.7%,在允许范围内,导致能效比有一定的误差。

(4)室内环境温度随着室内温度的增加,蒸发器内的换热温差增大,换热量增加,故换热增强。性能参数随室内温度的变化曲线见图7。由图7(a)可以看出,温度值T1缓慢减小、T2迅速减小、T3基本不变、T4迅速增加;由图7(b)可以看出,压力值p1/p4缓慢增加,p2/p3缓慢增加,这是因为室内温度的增加使蒸发温度也增加,对应的蒸发压力增加,故压缩机的吸气压力增加;由图7(c)可以看出,制冷剂的流量缓慢增加;由图7(d)可以看出,空调系统的能效比持续增加。因此,随着室内温度的增加,系统的能效比必然增加,调节室内温度以达到既舒适又节能的目的是非常有必要的。

(5)室外环境温度随着室外温度的增加,冷凝器的换热温差减小,冷凝器所能换走的热量减小,换热效果变弱,制冷剂在冷凝器中的液化不及时。性能参数随室外温度的变化曲线见图8。由图8(a)可以看出,温度值T1缓慢增加、T2迅速增加、T3迅速增加、T4缓慢减小;由图8(b)可以看出,压力值p1/p4缓慢减小、p2/p3缓慢增加;由图8(c)可以看出,制冷剂的流量缓慢增加;由图8(d)可以看出,空调系统的能效比持续减小。因此,室外温度的增会使系统的能效比减小,对于室外温度较高的地区,选择对应的空调机型很有必要。

5结论

通过建立一种空调系统稳态集总参数法热力学模型,对某种分体式空调进行模拟,与现有系统模型的计算结果进行对比,再对空调系统性能随运行参数,如电子膨胀阀的流通面积、压缩机转速、制冷量、室内环境温度、室外环境温度的变化进行分析。主要结论归纳如下:

(1)通过和现有模型的对比,发现提出的集总参数模型物理概念清晰,计算过程简明科学,迭代次数少,计算速度快,能够准确确定各部件进出口的热力参数,除个别点,该模型与现有模型所得结果稳合度很好,最大误差在10%左右;

(2)空调系统的性能随运行参数变化的结果是:随着电子膨胀阀的流通面积的增加,空调的能效比迅速增加;随着压缩机转速的增加,空调的能效比先增大后减小,当转速为3 220 r/min时能效比最大;随着制冷量的增加,空调系统的能效比先增大后减小,在制冷量为3 000 W时能效比最大;随着室内环境温度的增加,空调系统的能效比迅速增加;随着室外环境温度的增加,空调系统的能效比迅速减小。

参考文献:

[1]黄翔.空调工程[M].北京:机械工业出版社,2006.

[2]Hiller C C,Glieksman L R.Improving Heat Pump Performance Via Compressor Capacity Control-analysis and Test[R].Energy Laboratory Reports MIT-EL 76-001,MIT-EL76-002.Cambridge:Massachusetts Institute of Technology,1976.

[3]Sami S M,Duong T N,Mercadier Y.Prediction of the Transient Response of Heat Pumps[J].ASHRAE Trans,1987,93(2):471-490.

[4]Hamilton J F,Miller J L.A Simulation Program for Modeling an Air-Conditioning System[J].ASHRAE Transactions,1990,96(l):213-221.

[5]Chen Z J,Lin W H.Dynamic Simulation and Optimal Matching of a Small-scale Refrigeration System[J].International Journal of Refrigeration,1991,14(6):329-335.

[6]Geoffrey G H,Chen J.A Computer Simulation Program for Mixed-refrigerant Air Conditioning[J].International Journal of Refrigeration.1994,5(2):343-350.

[7]丁国良,张春路,李灏,等.分体式家用空调器动态仿真[J].上海交通大学学报,1999,33(3):262-265.

[8]朱瑞琪,谢家泽,吴业正.制冷系统的综合优化控制模型[J].西安交通大学学报,2002,36(5):461-464.

[9]杨志刚.小型制冷空调系统的稳态仿真[D].吉林:吉林大学,2005.

[10]王婷,陈海耿,赵巍,等.小型制冷系统的稳态模拟[J].中国工程科学,2007,9(3):97-102.

[11]张飞翔.小型制冷系统模拟研究[D].南京:南京理工大学,2011.

[12]Shao L L,Yang L,Zhao L X,et al.Hybrid Steady-state Modeling of a Residential Air-conditioner System Using Neural Network Component Models[J].Energy and Buildings,2012,50(2):189-195.

[13]While D D.The Measurement of Expansion Valve Capacity[J].Refrigeration Engineering,1935,(8):108-112.

[14]缪道平,吴业正.制冷压缩机[M].北京:机械工业出版社,2002.

[15]张华俊,文力,靳贵铭,等.制冷原理与性能[M].武汉:华中科技大学出版社,2008.

[16]周子成.全封闭滚动转子式制冷压缩机性能分析[J].流体工程,1987,16(10):52-59.

[17]李树林.空调用制冷技术[M].北京:机械工业出版社,1995.

One Lumped Parameter Model of Air-conditioning System

Chu Rui1,2,Yang Yuanjin1,2,Wang Liangbi1,2

(1.School of Mechanical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China;2.Key Laboratory of Railway Vehicle Thermal Engineering of MOE,Lanzhou Jiaotong University,Lanzhou 730070,China)

Key wordsAir-conditioning system;System modeling;Simulation;Lumped parameter method

AbstractThe research on air-conditioning system has important significance on improving system performance. Compared with the current air-conditioning system model,rather than respectively conducting modeling calculation on each parts of air conditioner interior and calculation of balance of systems after reaching to balance,the thermodynamic model of lumped parameter method built only chooses thermal parameter of each component models which is closely related to system simulation,establishes its model and settles iterative solutions directly to all the unknown variables at the same time. The thermodynamic model of lumped parameter method built features advantages of distinct physical concepts,simple and clear calculation process,less iterations and fast speed etc.

doi:10.16468/j.cnki.issn1004-0366.2016.03.013.

收稿日期:2015-01-26;修回日期:2015-03-17.

基金项目:国家科技支撑计划(2012BAA10B00).

作者简介:褚睿(1990-)，女，甘肃酒泉人，硕士研究生，研究方向为热能工程.E-mail:lovely2150@126.com. 通讯作者:王良璧.E-mail:lbwang@mail.lzjtu.cn.

中图分类号:TB61+1

文献标志码:A

文章编号:1004-0366(2016)03-0059-08

引用格式:Chu Rui,Yang Yuanjin,Wang Liangbi.One Lumped Parameter Model of Air-conditioning System[J].Journal of Gansu Sciences,2016,28(3):59-66.[褚睿,杨渊晋,王良璧.空调系统的一种集总参数模型[J].甘肃科学学报,2016,28(3):59-66.]