谈二次曲线束在解析几何中的应用

黄旭东

(湖北省黄石市第一中学，435000)



谈二次曲线束在解析几何中的应用

黄旭东

(湖北省黄石市第一中学，435000)

在解析几何中,我们常常利用曲线束解题,如过两相交直线交点的直线束,过两圆相交的交点的圆束，等等,其最大的作用是简化运算.下面谈谈二次曲线束在解几方面的应用.

一、知识梳理

二次曲线方程ax2+bxy+cy2+dx+ey+f=0,根据参数的不同值,可表示成椭圆、双曲线、抛物线等二次曲线.其实除了上述曲线之外,还可表示成两条直线．形如

(a1x+b1y+c1)(a2x+b2y+c2)=0

的方程也为二元二次方程,可看成退化的二次曲线.

一般地,两条二次曲线通常有四个交点(这些交点可能有重合,也可能有虚的)，如果两条二次曲线的方程分别为f1(x,y)=0,f2(x,y)=0(其中f1(x,y),f2(x,y)是关于x,y的二次式),则过这两条二次曲线交点的二次曲线束的方程可写成μf1(x,y)+λf2(x,y)=0(λ,μ为不全为0的实数).

二、应用

1.处理四点共圆问题

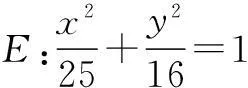
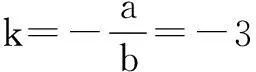
例2已知抛物线E:y2=2px(p>0)上一点M(x0,4) 到焦点F的距离

(1)求E的方程;

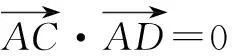
解(1)y2=4x,过程略.

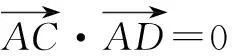
评注对于圆锥曲线中四点共圆的综合题,用常规法一般计算量大,甚至非常繁琐,而用二次曲线束可表示为圆,其方程xy系数为0,x2,y2的系数相等,再组成简单的方程组解方程,大大化解了设直线求交点及解复杂方程组的繁琐运算,同时也避免了为了运用四点共圆中的几何性质而煞费心机地反复转换,使解题过程变得简洁而高效!

2.求解定点与定值问题

(1)求椭圆E的方程;

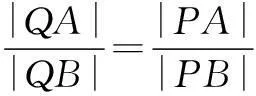
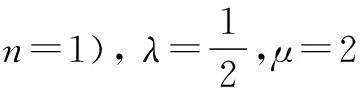
(1) 设动点P满足PF2-PB2=4,求点P的轨迹；

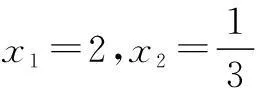
(3) 设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).

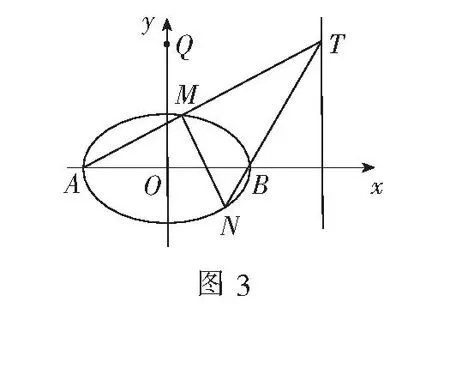
解(1)、(2)略.

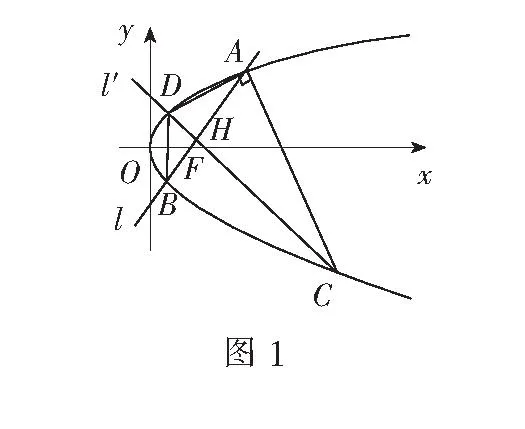
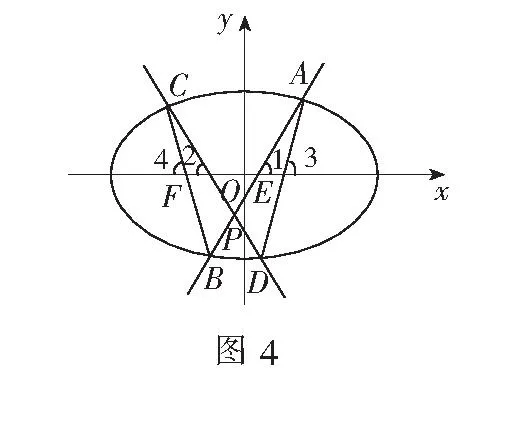
例5如图4,AB,CD是中心为O的椭圆的两条相交弦,交点为P,两弦AB,CD与椭圆长轴的夹角分别为∠1,∠2,且∠1=∠2,求证:|PA||PB|=|PC||PD|.

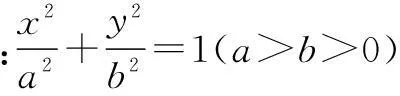
μ(mx+y+s)(-mx+y+t)

+λ(b2x2+a2y2-a2b2)=0.

①

设直线BC,DA的方程分别为a1x+b1y+c1=0与a2x+b2y+c2=0,则BC,DA组成的退化二次曲线束的方程为

(a1x+b1y+c1)(a2x+b2y+c2)

=0.

②

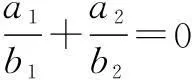
设直线AD与CB分别与x轴交于点E,F,则由上知∠3=∠4,又∠1=∠2,故∠3-∠1=∠4-∠2，即∠BCP=∠DAP,又∠CPB=∠APD,故∆BPC∽∆APD,故有

也即|PA||PB|=|PC||PD|.

评注例3,例4为证明定点问题,例5本质上是证明kBC+kAD=0的定值问题,它们都涉及到两相交直线与圆锥曲线相交问题,在应用双直线组成的二次曲线束处理此类问题时，运用技巧步骤为:(1)先由相交两直线AB,CD组成二次曲线束(a1x+b1y+c1)(a2x+b2y+c2)=0；(2)双直线与圆锥曲线相交于四点(可能为重合点或虚点)，它们组成过这四点的二次曲线束μ(a1x+b1y+c1)(a2x+b2y+c2)+λf(x,y)=0；(3)变换两直线与圆锥曲线交点次序组成新的二条相交直线,写出或设出其方程,重新组成新的双直线的二次曲线束(A1x+B1y+C1)(A2x+B2y+C2)=0；(4)原来的二次曲线束与新组成的双直线的二次曲线束都过相同四点,故方程μ(a1x+b1y+c1)(a2x+b2y+c2)+λf(x,y)=0包含新的二次曲线束(A1x+B1y+C1)(A2x+B2y+C2)=0,比较系数列方程求解即可．

综上所述,灵活运用二次曲线束解题,可避免求根的复杂运算,起到优化解题的效用．因此在平时的教学时,适当拓展一些解题技巧与方法,可开拓学生的视野,提高学生的技能与能力,从而更好的应对高考的要求,不失为一种可行的途径．当然不能舍本求木,走向另一极端,平时高考复习中,还是强调基础与通法为主,技巧兼顾,以更好适应高校人才挑选的要求．