例谈一类不等式的应用问题

张　刚

(安徽省宿州市埇桥区祁县中学，234115)



例谈一类不等式的应用问题

张刚

(安徽省宿州市埇桥区祁县中学，234115)

基本不等式是高中数学的重要内容之一,也是每年高考数学考查的热点内容之一. 使用基本不等式,要紧扣“一正二定三相等”的原则,这是使用基本不等式解决数学问题的关键.但是有些数学问题看似属于常规基本不等式模型,仔细分析,并不符合常规基本不等式使用的条件,很多学生遇到这类问题,往往不知所措,乱用公式,从而导致考试时大量失分,实在得不偿失.本文结合几例,谈谈如何破解这类不等式的应用问题,现抛砖引玉如下,供大家参考.

一、 分离系数,借助单调性

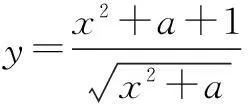
解将函数解析式变形，得

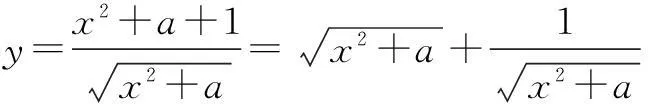
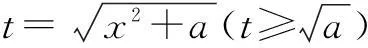
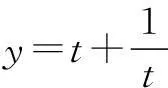
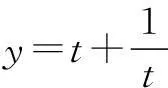
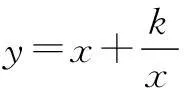
解由f(x)≥3变形，得

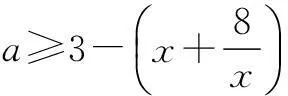
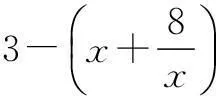
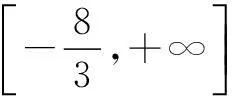
评注x∈N*,说明自变量是连续的正整数,对应函数的图象也就是一些孤立的点,其单调性只能通过点的高低具体判断.

二、 和为定值,巧妙换元

例3已知实数x,y,z,满足x+y+z=1,x2+y2+z2=3,则z的最大值为______.

解x+y=1-z,

x2+y2=3-z2,

则(x+y)2=x2+y2+2xy

≤2x2+2y2

=6-2z2,

得(1-z)2≤6-2z2,

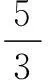
评注本题难点在于灵活运用基本不等式,通过换元,获得关于z的不等式 (1-z)2≤6-2z2.

三、 化“多”为“单”,利用导数

例4实数a,b,c满足a+b+c=9,ab+bc+ca=24,求abc的取值范围.

解由已知，得a+b=9-c，

ab=24-(a+b)c=24-c(9-c).

又(a+b)2=a2+b2+2ab≥4ab,

所以 (9-c)2≥96-36c+4c2,

解得1≤c≤5.

又abc=[24-c(9-c)]c

=c3-9c2+24c.

所以本题即求f(c)=c3-9c2+24c在[1,5]上的值域.利用导数法可知函数f(c)在区间(2,4)上单调递减,在区间(1,2),(4,5)上单调递增.又易知f(1)=f(4)=16,f(2)=f(5)=20,所以16≤f(c)≤20,故abc的取值范围为[16,20].

评注本题求解需要关注两点:一是准确分析c的取值范围(利用基本不等式及解不等式法);二是转化目标式,构造函数,利用导数法求取值范围.

四、 抓住整体,降次换元

例5若x>0,则函数

的最大值为______.

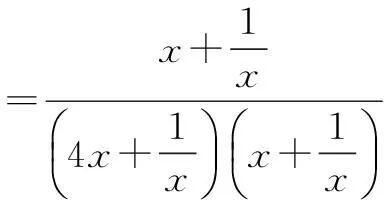
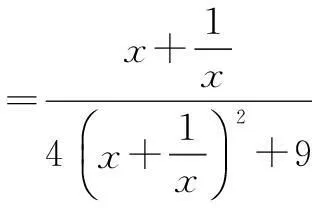
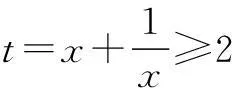
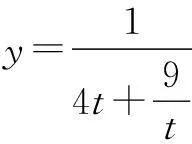
又易知新函数在[2,+∞)上单调递减,

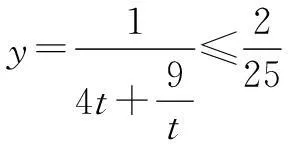
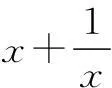
五、 利用性质,合理构造

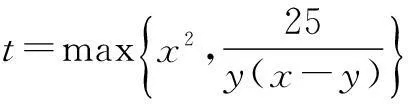
解法1由题意知

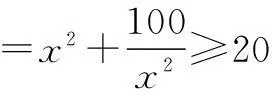
所以2t≥20,即t≥10，最小值为10.

解法2由题意，知

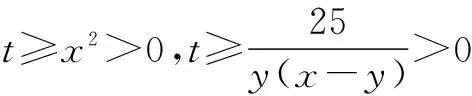
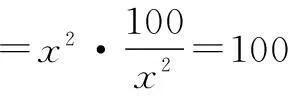
所以t2≥100,即t≥10，最小值为10.

评注求t=max{f(x),g(x)}的最小值问题,可利用2t≥f(x)+g(x)的性质求解;当f(x)>0,g(x)>0时,可利用t2≥f(x)g(x)的性质求解.