“导数的应用（一）”教学设计

姚贵丰郭桂芳



“导数的应用（一）”教学设计

姚贵丰郭桂芳

教材分析

教材内容：本节课是人教版高中数学选修2-2第一章第四节“生活中的优化问题举例”第一课时，主要内容是用导数求生活中面积、体积的最值问题。

地位和作用：生活中的优化问题是在导数的概念、运算，用导数求极值、最值等内容的基础上教学的，它既是对导数知识的复习巩固，也是导数知识在实际生活中的应用。本节课以生活实例为题材，培养学生的阅读能力和建模意识。学习过程中的认知冲突，不同思维的碰撞，易激发学生思维的积极性，有助于创新能力的培养。

学情分析：学生刚学完导数的概念、运算、用导数求极值、最值等知识，为用导数解决实际生活中的问题创造了条件。高二年级的学生正值身心发展的鼎盛时期，思维活跃，并有相应的认知基础，乐于探索、敢于探究。但逻辑思维能力还属于经验型，运算能力不强，数学建模方法的运用还不够熟练，有待进一步加强训练。

教学目标

知识与技能：掌握利用函数思想、导数方法求有关面积、体积的最值问题。

过程与方法：以日常生活、生产实践中典型的问题为载体，探讨利用函数思想、导数方法求面积和体积问题的应用。

情感态度与价值观：学生分享将实际问题转化为数学问题的学习乐趣，感受数学与生活的密切联系。

重点、难点

重点：从实际问题中抽象出函数模型，用导数方法求解函数最值问题的程序化步骤。

难点：对最值、最值与极值概念的区别与联系的理解。

教学过程

一、创设情境，复习引入

以本班学生参加元旦汇演的图片引入。K1303举行了2016年的元旦迎新活动，数学兴趣小组就活动前的海报设计和活动后海报的再利用进行了如下课题探究活动。下面我们一起再现他们的活动过程。

设计意图：以学生成功的活动经历引入，激起学生的学习兴趣。

二、活动设计，培养创新思维

探究一：如果海报为如下图所示的竖向张贴的海报，要求版心面积为128dm2，上、下两边各空2dm，左、右两边各空1dm。若海报版心高为xdm，

1.求四周空白面积关于x的函数解析式；

2.求四周空白面积最小值。

探究二：若海报材料用的是长20dm、宽10dm的长方形硬纸板，活动结束后，兴趣小组准备将海报做成废品收集箱进行再利用。如下图所示，从长方形纸板的4个角上分别切去面积相等的正方形，再把纸板的边沿虚线折起，用胶粘好，做成一个无盖的长方体箱子。问废品收集箱底面的长、宽分别是多少时，其容积最大，最大容积是多少。

探究三：兴趣小组将另外两张废弃海报用胶纸拼成如下图所示的边长为20dm的正方形ABCD，切去阴影部分所示的4个全等的等腰直角三角形，再沿虚线折起，使得4个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E，F在AB上，是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xdm。

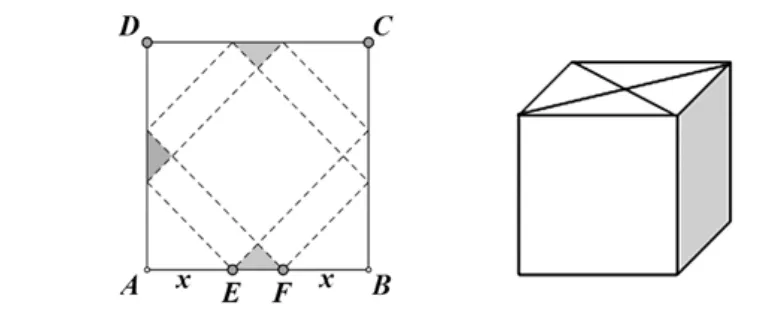
（1）包装盒要显得更大气，因而要增大包装盒的侧面积。试问x取何值时，包装盒的侧面积S（dm2）最大？

（2）另一同学认为包装盒要更适用，因而要使包装盒的容积最大。但限于某种原因，x∈（0，c]，（c∈（0，10]的常数），试问x应取何值时，包装盒容积V （dm3）最大？并求其最大值。

（3）先学后教，以学定教

教师让学生欣赏元旦汇演的图片后，引入探究一。学生思考后进行解答。观察到学生用基本不等式求解面积最值时，教师抓住契机提出问题，引入导数作为工具，求面积、体积的最值。教学探究三时，教师让学生先分组讨论，然后概括思路，再由学生作答。教师通过实物投影仪当堂评价，并就学生学习中出现的问题进行现场讲评，做到举一反三。

三、练习巩固，融会贯通

教师设计了两组检测题，学生根据各自的学习基础自主选择，力求做到人人可检测，个个有收获。

A组

1.用长为20cm的铁丝围成两个正方形，若其中一个边长为xcm，设两个正方形的面积之和S=f（x），则正确的是（ ）。

A.f（x）的定义域是[0，5]

B.f（x）=x2+（5-x）2（0＜x＜5）

2.要做一个底面为长方形的带盖的箱子，其体积为72cm3，底面两邻边边长之比为1：2，则它的长为_____，宽为_____，高为_____时，表面积最小。

B组

1.把长为100cm的铁丝分成两段，围成一个正方形与一个圆，那么怎样分，能使它们的面积之和最小？

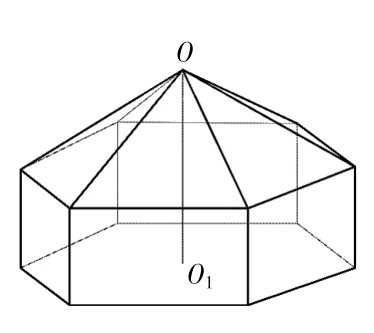
2.请同学们设计一个帐篷。它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如右图所示）。试问当帐篷的顶点O到底面中心O1的距离为多少时，帐篷的体积最大？

四、总结反思，提升经验

学生谈谈对这节课的收获，教师利用学生的反馈，引导学生进行总结反思，及时提升经验。

（作者单位：长沙市第二十一中学）