大跨径桥梁施工控制温度应力问题

陶文景

(贵州贵安建设投资有限公司，贵州　贵安　550025)

大跨径桥梁施工控制温度应力问题

陶文景

(贵州贵安建设投资有限公司，贵州贵安550025)

关键词：大跨径桥梁；温度应力；施工控制

0引言

桥梁施工安全与成桥状态能否符合设计要求是人们关注的重点问题，要实现高质量施工，只通过简单的检查与验收显然是具有很大难度的，所以需要对桥梁施工进行严格的控制，确保实际的施工状态与设计预期一一对应。结构设计参数主要用于衡量结构状态变化，若参数改变，则结构内力必然会出现相应变化。在众多结构参数当中，温度参数的确定难度较大，属于复杂变量，和所在地理位置、方向以及材料等有关，在明确结构应力中有着十分重要的作用，而且也是最难进行识别的重要参数。因此，针对温度应力开展深入的研究工作是施工控制的关键环节，是实现最佳成桥状态的重要举措。

1温度应力

1.1温度应力的产生

在分析温度应力的早期，人们通常将年温变化的产生与分布作为依据，随着研究的进一步深入，人们逐渐认识到非线性特点对于研究的重要性。近几年，伴随研究成果的不断更新，温度应力研究已经从过去的单一考虑气温条件上升至充分考虑日照条件的高度。对于大跨径桥梁而言，温度应力主要分成两种形式，分别为：结构物某种构件单元内，由于各纤维温度不尽相同而形成的应变差在约束的作用下产生的应力，这种温度应力被称为温度自应力；在结构或者是体系当中的各个构件，由于其温度存在一定差别而形成的结构变化，会在支承约束条件下生成应力，这种应力即为温度次应力[1]。研究还发现，温度应力的产生与分布不仅具有非线性，还具有十分显著的时间性。

1.2温度应力效应类别

大跨径桥梁由于受到自然条件等因素的影响会出现温度效应，一般而言，这种温度效应可以分成两种类型，分别为：年温差效应与局部温差效应。其中，年温差效应为改变迟缓的年温差，它会影响到桥梁截面的温升、温降以及伸长、缩短，桥梁位移在受到一定约束后，会生成温度次应力[2]。局部温差效应因为日照辐射生成，其在各种截面上的传热形式均不相同，具有非线性分布特征，而且，截面非线性温度分布所造成的胀缩和截面形变之间存在的差别，会使所有种类的截面都会出现自应力。

2大跨径桥梁温度应力计算

2.1基本假定

在对温度应力进行计算的过程中，基本假定是首要环节，具体内容如下：

(1)假设梁长方向中的温度分布均匀，同时省略掉局部温度变化所造成的差别；

(2)假设混凝土结构的材料是均匀，且各向同性的，在生成裂缝前，满足各项基本规律；

(3)假定截面不变且可用；

(4)根据温度荷载理论对应力进行计算；

(5)采用叠加法等计算出多种荷载情况下的应力。

2.2温度应力计算

在桥梁结构当中，若实际的分布曲线给定，如图1所示，则可据此求出应力分布。

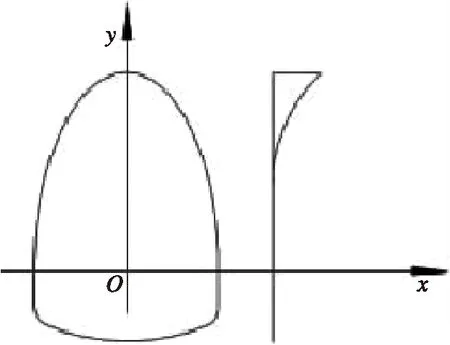
图1　桥梁结构温度分布曲线图

首先，假定结构中各种纤维均自由伸缩，则可得应力：

εT(y)=αT(y)

(1)

式中，a——膨胀系数；

T(y)——具体温度分布。

依据假设的平截面，可得总应变：

ε(y)=εc+ky

(2)

式中，εc——重心位置应变；

k——微段曲率。

因为总应变和温度应变不相同，所以可以得出一定几何关系：

ε(y)=εT(y)+εe(y)

(3)

式中，εe(y)——弹性应变，其应力可表示为：

σe(y)=Eεe(y)=E[ε(y)-εT(y)]=E[εc+ky-εT(y)]

(4)

截面内力可表示为：

NZ=∫Aσe(y)dA

=E∫A[εc+ky-εT(y)]dA

=EεcA-E∫AεT(y)dA

(5)

Mx=∫Aσe(y)ydA

=E∫A[εe+ky-εT(y)]ydA

=kEI-E∫AεT(y)ydA

(6)

根据式(5)与式(6)可得：

(7)

(8)

式中：E——弹性模量；

A——截面的面积；

I——抗弯惯矩。

针对超静定结构而言，如果将温度的赘余力表示为xi(i=1，2，…，n)，则在xi为1时，截面产生的内力为：

(9)

(10)

将式(9)、(10)代入式(7)、(8)中可得：

(11)

(12)

εc、k为已知条件，则可得出赘余力xi方向形变，在此基础上，通过形变协调条件对xi进行求解后即可得出应力：

σe(y)=E[εc+ky-εT(y)]

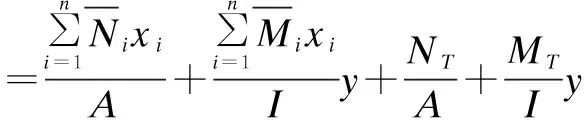
(13)

式中：

NT=E∫AεT(y)dAMT=E∫AεT(y)ydA

由式(13)得知，温度应力主要由两部分构成，分别为次应力与自应力：

(14)

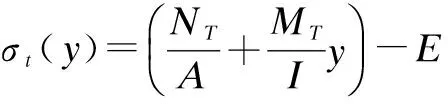
(15)

3工程案例分析

3.1工程概况

总干渠高大跨渡槽C2标由河沟头、焦家2座渡槽组成，河沟头渡槽主槽采用(80.55+2×150+80.55)m共461.1 m连续刚构体系；焦家渡槽主槽采用(95.95+2×180+95.95)m共551.9 m连续刚构体系。渡槽平面、纵向均位于直线上，渡槽箱梁顶面纵坡1/1 500，靠进口侧高，靠出口侧低。其中，河沟头箱梁跨中截面梁高4.6 m，是主跨径的1/32.61，墩顶梁高11.5 m，是主跨径的1/13.04；焦家箱渡槽梁跨中截面梁高4.6 m，是主跨径的1/39.13，墩顶梁高13.8 m，是主跨径的1/13.04。

3.2温度观测

研究发现，温度的改变是使主梁出现挠度的主要原因之一。相对之下，日温变化趋于复杂，特别是在受到日照等作用时，主梁的顶、底板温差较为明显，使得主梁出现挠曲现象，而且还有可能使墩身发生位移。而季温造成的实际影响则较为简单，变化趋势可以保持恒定，对各节段温度进行准确收集，并输入至计算机当中，借助相关软件进行计算分析，即可求出挠度数值。为进一步掌握截面温差情况，还要在被测梁体上设置多个测点，以及时获取温度变化情况。

3.2.1测点设置

设置两个截面，每个截面分别设置14个测点，把铂电阻设置在钢筋上，经防潮处理以后，埋置混凝土中，再将导线布置在结构表面。

3.2.2观测结果

分析得知，梁高温度分布和T(y)=T0ye-Cyy十分接近，如图2所示。

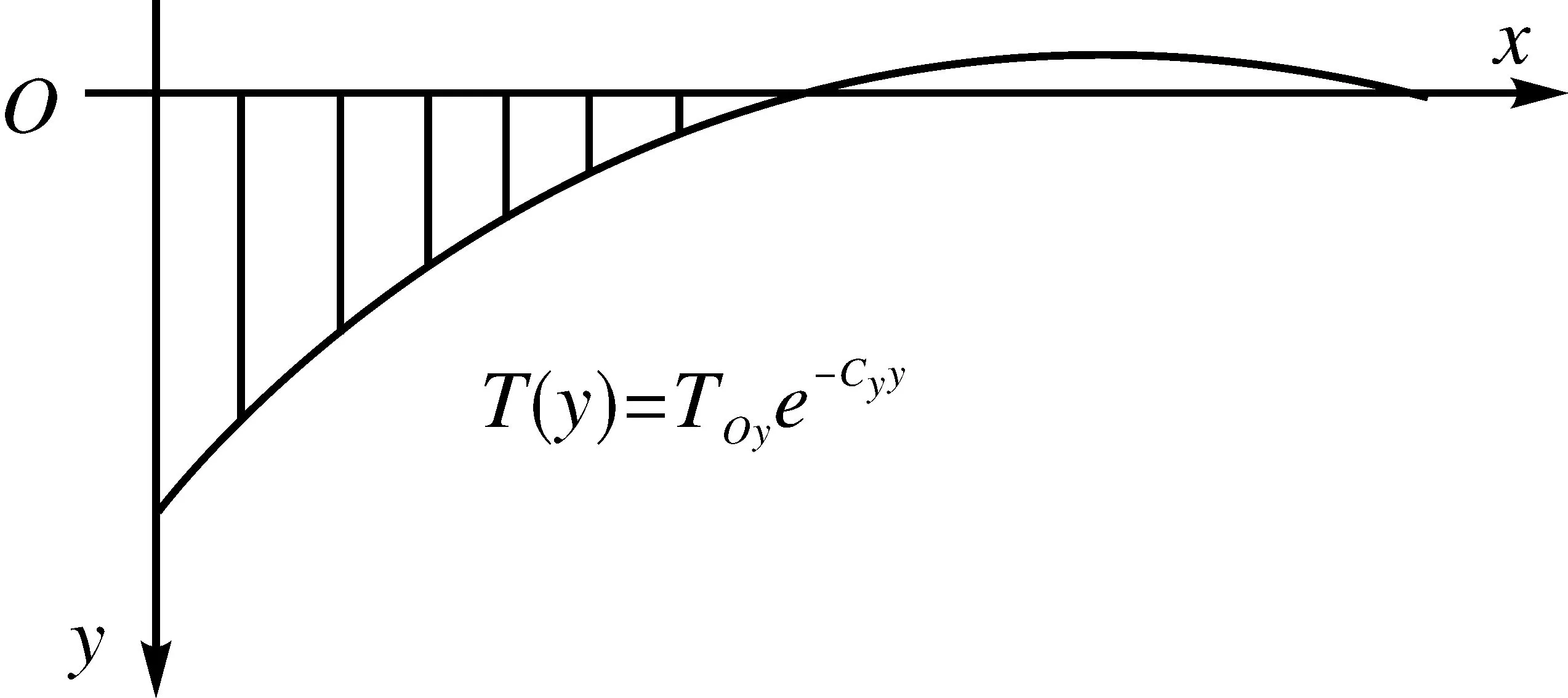
图2　温度分布示意图

3.3计算分析

基于观测结果方面的考虑，使用T(y)=T0ye-Cyy分布函数，根据应力叠加规律可得总应力为：σe(y)=σt(y)+σtx(y)。

结合上述公式，算出应力。首先，计算非线性温度条件下所产生的截面应变；然后，获取初应力，使用形变协调理论计算次应力与次内力。为对结构形变所造成的温度变化进行分析，箱梁顶板的升温与降温分别选为1 ℃、3 ℃与5 ℃，可表示为：T0y=20 ℃±(1 ℃、3 ℃、5 ℃)，cy=5，同时按照温度递增工况实施运算，只考虑温度造成的影响。

3.4施工温度应力控制方法

3.4.1结构形变控制

充分结合计算成果与实测数据，调整监控参数，得出不同阶段对应的形变数值，保证不同块件标高的实际值、预测值与设计值保持相同的变化趋势。

3.4.2结构应力控制

综合考虑温度、徐变与收缩等因素，通过实测、计算结果对比，对监控参数进行实时调整，确保结构应力的实际情况与预测结果变化保持一致[3]。

4结语

(1)温度参数是一种极其复杂的变量，对于应力与形变确定至关重要，所以在施工中应对温度控制给予足够的重视。

(2)在研究温度应力的同时，可根据假定的条件提出一系列计算公式，同时充分使用这些公式得出温度变化造成的形变影响。

(3)结构变位与温度分布存在紧密的联系，施工时应确保数据结果的真实性，进而保证施工控制更具合理性与有效性。

参考文献

[1]王力强，高猛.大跨径桥梁施工控制温度应力研究[J].广东公路交通，2010(1)：24-27，30.

[2]张浩.桥梁施工控制中的温度应力研究[J].交通标准化，2010(13)：75-79.

[3]吴文阳.大跨径桥梁施工控制温度效应研究[J].科技资讯，2006(2)：111-112.

摘要：文章分析了大跨径桥梁温度应力产生的形式与效应类别，提出了一套实用的应力计算方法，并结合实例介绍了大跨径桥梁施工温度应力控制方法。

Large-span Bridge Construction Control Temperature Stress

TAO Wen-jing

(Guizhou Gui’an Construction Investment Co.，Ltd.，Gui’an，Guizhou，550025)

Abstract：This article analyzed the forms and effect category of large-span bridge temperature stress，put forward a set of practical stress calculation methods，and in combination with examples，it intro-duced the construction temperature stress control method of large-span bridges.

Keywords：Large-span bridges；Temperature stress；Construction control

作者简介

中图分类号：U445.4

文献标识码：A

DOI：10.13282/j.cnki.wccst.2016.04.021

文章编号：1673-4874(2016)04-0075-03

收稿日期：2016-03-27

陶文景(1974—)，高级工程师，研究方向：高墩大跨桥梁施工。