巧设矛盾促进概念教学

刘远琴

【摘要】从哲学上看，矛盾关系普遍存在于世界上的一切事物之中.随着素质教育理念的深入，传统概念教学中的一些弊端逐渐显现出来.为了提升学生在教学中的主体地位，充分发挥其主观能动性，可以从概念的引人、生成、辨析、巩固四个阶段来设置矛盾，从而促进概念教学.

【关键词】矛盾；概念教学

矛盾是小说创作中较为普遍的一种创作手法，它可以使文章增添色彩和魅力.它的应用推动剧情的发展，进而达到高潮，引起读者共鸣.可以说没有矛盾就不可能是一部精彩的小说.概念课作为数学教学的基础，对于数学教学的质量有着直接的影响，对于学生后续的学习有着举足轻重的作用.由于概念课枯燥和抽象，学生普遍反映难度较大.我们如果能在概念教学的某些环节中适当适时的设计一些矛盾，必能在解决矛盾的过程中使学生的求知欲、探索欲得到激发，进而思维得到拓展.本文就概念教学中如何巧设矛盾，提高数学课堂教学效率，提供本人在教学过程中的几个教学设计，与大家共享.

1.引入概念时巧设矛盾，激发学生兴趣

良好的开端是成功的一半.概念教学的第一个环节是引入，无论是从学习内容本身，还是从生活实际中引入，我们在讲授概念之前都可以创设一些矛盾，让学生的求知心理和情境内容之间产生冲突，快速吸引学生的注意力，使学生迅速进入状态，激发学生的求知欲，产生一种迫切想知道答案的好奇心理.正如托尔斯泰所说“成功的教学所需的不是强制，而是激发学生学习的兴趣.”

案例1 等比数列的前n项和的教学引人

兔子上次比赛因为睡懒觉输给了乌龟，他觉得不服气，于是他找到乌龟要求和他重新比赛.乌龟想了想，回答说：“没问题，我可以和你比，但是你腿长我腿短，比赛不公平.如果让我用滑板，我们就比一比.”假设兔子每分钟最多可以跑100米，乌龟踩着滑板加速前进，在第一分钟滑1米，第二分钟滑2米，第三分钟滑4米，……即后一分钟为前一分钟的2倍.大家想想看，十分钟后谁会领先.此问题一出，立即引起了学生极大的兴趣，学生们立刻活跃起来.当即写出兔子十分钟内所跑的路程是1000米，而乌龟在滑板的帮助下所跑过的路程是1+22+23+24+…+29，要知道结果只能逐项求和.教师这时顺势提出是否有更便捷的算法.如此教学，使学生的心理激起层层涟漪，对接下来的学习充满了期待，一旦学习的热情高涨，自然对马上要学的内容产生了浓厚的兴趣.

2.生成概念时巧设矛盾，促进理解

概念教学必然要经历概念的生成.而学生可以通过概念形成和概念同化两种方式获得概念，不管是哪种方式的获得都需要教师能找准概念产生的基点，使学生在教师的引导下进行主动、积极的探索.如果我们能在概念的生成过程中适当的创设矛盾则更能刺激学生探求新知的欲望.

案例2 在棱柱的概念生成教学时我们可以这么设计教学：

师：通过观察我们熟悉的粉笔盒、螺杆的头部，三棱镜等等，我们会发现他们都呈棱柱形状，他们的每个面都是平行四边形，并且相对的两个面给我们以平行的感觉.小明由此得出只要满足有两个面互相平行，其余各面都是平行四边形的多面体就一定是棱柱.请问小明同学的说法是正确的吗？

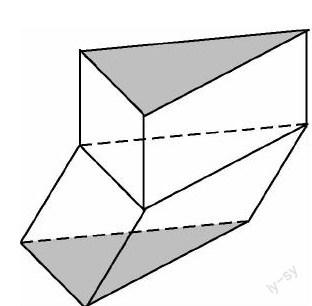
多数同学凭着原有对棱柱的印象觉得确实是这样，表示赞同，但有一小部分同学因为提前预习了棱柱的概念从而对这个说法表示怀疑.这时甲同学站了起来说：“我认为小明的说法是错的，应该说棱柱一定会满足是有两个面互相平行，其余各面都是平行四边形的多面体，但满足这两个条件的多面体不一定是棱柱.大家看看我画的这个多面体（如右图），它是不是棱柱？”同学们看完后顿时惊呼，从而明白棱柱只满足这两个条件是不够的.教师这时可以引导学生得出正确的概念.

这种巧设矛盾生成概念的方法比由老师直接讲授概念让学生印象更深刻.在归纳出概念的同时还培养了学生思考问题的缜密性，严谨性，让学生积极开动脑筋，主动参与到概念的生成当中，成为课堂的主人，而不是被动的接受者.

3.辨析概念时巧设矛盾，增进理解

概念形成之后学生虽然对概念有了一个初步的认识和大致的理解，但是对概念的内涵和外延未必有真正的掌握，对概念的理解往往会比较片面和肤浅，因此学生在概念形成后需对其进行及时的辨析.这时在易错的概念中巧设矛盾，让学生在辨析概念的过程中真正理解掌握概念，把对概念的理解渗透到解题的每一个环节，优化学生的思维品质.

教师把这种解法展示出来，请学生评判解法.几乎所有的学生都认为此题的解法是正确的.这是由于学生对单调性定义理解不够透彻造成的.于是我让学生先回顾单调性的定义及其中的关键字眼，然后再来评判.经过一片沉思，同学甲立即站起来说：“定义中的关键字眼有任意两个字，上述解法只满足了在两个区间上面分别是递增的，但未必在整个定义域内都递增.”这时还是有很多同學很困惑不是很理解.这时同学乙站了起来说：“我可以举一个反例来说明上面做法的错误.当a=9时，取两个自变量x1=1，x2=3，得到的结果是f（1）=6>f3=12.显然这与单调递增相矛盾.”同学们顿时醒悟，那该怎么做呢？教师引导学生通过画图分析得出正确解法.这样的争论使学生对单调性的定义有了进一步的理解，从中培养了学生的科学探究意识和细致的分析能力，增强了学生数形结合运用的能力.

学生在概念理解中出现的错误所引发的认知冲突，是推进概念教学的一种重要资源.教师在教学中要能及时捕捉学生原始生成的普遍错误，让学生主动发现错误并及时纠正，进而增进对概念的理解，

4.巩固概念时巧设矛盾，深化理解

学生获得概念后如不及时巩固就容易遗忘、混淆.这就需要在巩固概念知识的过程中巧设矛盾，引发学生展开辩论，从辩论中发现自身错误.这样就激活了学生的思维，让学生对概念有了更深刻的理解.一方面提高了学生运用概念的能力，另一方面也培养了他们分析问题和解决问题的综合能力.

显然这两种答案不一样，一种是直接按题目的要求根据割线的斜率来求解，另一种是认为割线的斜率就是切线的斜率，因而转化为切线的斜率来求解.这两种解法好像都对，学生在课堂上就这两种不同的解法形成了两派并展开了激烈的讨论.矛盾的焦点集中在割线的斜率是否就是切线的斜率.这就需要回到切线的斜率和割线的斜率的定义中去寻找答案.通过比对概念和进一步的分析学生做出了正确的判断.

学生经历了这次不同解法中产生的矛盾冲突，对割线的斜率和切线的斜率这两个易混概念有了更清楚的认识.矛盾在不经意间产生的同时其实也给每个学生营造了一个探究的契机，让他们的思辨欲望得到有效的激发.对概念的理解在对与错的辨析中得到进一步的深入和巩固.

总之，适当适时的创设矛盾可以充分调动学生学习的兴趣，激发学生的研究热情，培养学生的探究能力.使学生在数学概念的生成、理解、巩固、深化的过程中，对数学概念有了更加全面和深刻的认识.矛盾让学生的理性思维得到锻炼和升华.

【参考文献】

[1]林生.新概念获得的方式及教学策略.中学数学，2011（1）.

[2]陈敏.矛盾冲突—学生思维发展的“推进器”.中学数学，2011（8）.