任意角的三角函数定义引入的微课教学设计

张军钢

设计的意图：“任意角的三角函数的概念”的教学设计应注意通过与“锐角三角函数”概念的因袭与扩张关系，引导学生参与“定义任意角三角函数的过程”.有了适切的“立意”，借助怎样的载体来落实，也是一个值得细究的问题.那么，以“锐角三角函数的概念”作为任意角三角函数的知识生长点是否合适？“锐角三角函数的概念”是以直角三角形为载体，关注的是“解决直角三角形的边角关系问题”，而对它的函数本性的认识并不是重点，锐角三角函数并没有被纳入函数概念体系中.因此，要使锐角三角函数概念成为教学的起点，还需要一个较长的过程铺垫：回顾定义——坐标化（全新的学习）——“单位化”（取r=1，全新的学习），而且学生可能无法把任意角的三角函数的概念纳入到函数的概念中.

因此，还有一种想法是在函数概念下以“圆心在原点的圆周上的点的坐标”随角的变化而变化的“操作、观察”，先让学生建立起“任意给定一个角α，圆周上就有唯一的一个点P（x，y）与之对应”的直观感受，把注意力集中在三角函数的“函数特性”上，能使学生认清其对应关系、定义域和值域等，从而真正把握三角函数的“本来面目”.是否可以在“函数是描述客观世界变化规律的数学模型”的思想指导下，以“如何建立圆周运动的数学模型”为教学起点，调动象限角、弧度制、单位圆、锐角三角函数等相关知识，在建立函数模型的过程中水到渠成地引入任意角三角函数的概念.这样，既可以使学生知道这一概念的背景、解决的问题，也可以使他们感受运用函数概念建立模型的过程和方法，还可以让他们体会三角函数在物理学科中的重要性.如果这样的设计思想能够实现，那么其效果是一举多得的.以下为笔者在教学实践中对任意角的三角函数定义引入的微课设计.

一、教材分析

三角函数是函数的一个基本组成部分，也是一个重要组成部分，在整个高中以至于大学都会经常用到三角函数的知识.初中已经学习过锐角的三角函数，教材第一节学习了任意角的表示方法，这些是学习任意角三角函数的基础.本节课的主要内容是：正弦、余弦、正切的定义；正弦、余弦、正切函数的定义域.

二、教学目标

理解任意角的三角函数的定义.

三、重点，难点

1.重点：任意角的正弦、余弦、正切的定义；

2.难点：任意角的三角函数概念的建构过程；

四、教学情景设计

1.引 入

我们初中已经学习了锐角三角函数，知道它是以锐角为自变量，

以比值为函数值的函数，那么高中为什么还要继续研究呢？

实例导入：“离离原上草，一岁一枯荣.野火烧不尽，春风吹又生.”（王安石诗）.诗中描绘的是自然界中“按一定规律周而复始”的现象，称之为“周期现象.”我们曾学习过用“指数函数”模型刻画人口增长问题，用“对数函数”的模型刻画地震的震级变化，用怎样的数学模型来刻画周期现象呢？“周期现象一般与周期运动有关”，一个简单而基本的例子便是“圆周上的一点旋转运动”.

2.探 究

情境——选择数学模型.

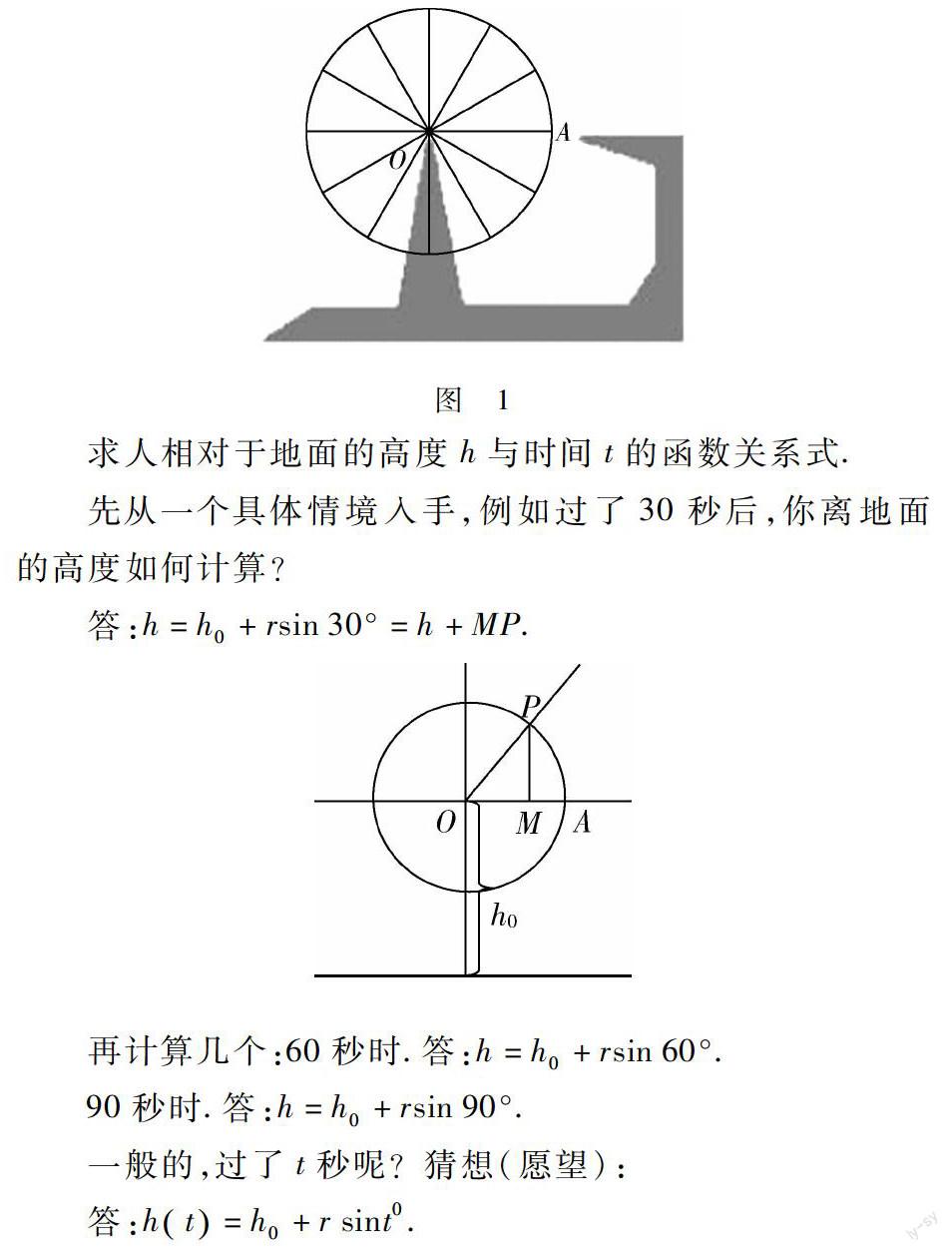
问题：摩天轮的中心离地面高度为h0，它的直径为2r，逆时针方向匀速转动，转动一周需要360秒，若现在你坐在座舱中，从初始位置点A 出发（如图1所示）.

求人相对于地面的高度h与时间t的函数关系式.

先从一个具体情境入手，例如过了30秒后，你离地面的高度如何计算？答：h=h0+rsin30°=h+MP.

再计算几个：60秒时.答：h=h0+rsin60°.

90秒时.答：h=h0+rsin90°.

一般的，过了t秒呢？猜想（愿望）：

答：ht=h0+rsint0.

“這样的想法合情，但合理吗？”

（意图：先从几个特殊情形出发，而后猜测一般性结论，再进行合理性论证！）

总结：人距离地面的高度h=h0+MP，其中h0是不变量，MP表示点P 到水平位置OA的距离，是变量；可以通过点P旋转的角度∠POA的大小，再结合初中锐角三角函数来计算.

3.分析数学模型

问题：对任意角∠POA；sin∠POA该如何定义？对前面这个问题往下具体分析：

当时间为t秒时，人距离地面的高度用h=h0±MP来表示，其中MP 表示点P到水平位置OA的距离.

对比：h=h0±MP与ht=h0+rsint0.

愿望：要想两者和谐统一.

必须有：rsint0=±MP即：sint0=±MP/r.

小结：点P在圆周上旋转运动，引起∠POA的变化，对任意一个确定的∠POA对应着唯一点P，进而有唯一的MP，得到sin∠POA=±MP/r①.

提问一：①式的分子何时取正值，何时取负值？

答：OA上方为正，OA下方为负.

提问二：根据①式这些特点，用怎样的一个量来替代MP或-MP，可以使上面的表示更简洁？

答：建直角坐标系，利用P的纵坐标替代MP或-MP.

4.建构三角函数的定义

任意的角的正弦一种定义方法.

（1）把α“放到直角坐标系内”.

（2）以原点为圆心，半径r 作圆，

又与α的终边相交于点P 坐标为（x，y）.

（3）规定：sinα=yr.

5.分析：以上规定是否合理？

问题一：当α为锐角时，此规定与初中定义矛盾吗？

结论：不矛盾，而且坐标法的引入摆脱了锐角的束缚.

问题二：圆的半径r大小有限定吗？

结论：根据相似三角形的知识，对于确定的角α，这个比值不会随点P在α的终边上的位置的改变而改变，是唯一确定的.

问题三：半径r取多少时，会使得比值更加简洁？

结论：可以考虑取r=1，这样的圆我们称单位圆.

即：在直角坐标系中，以原点为圆心，以单位长度1为半径的圆.

（意图：可以打破知识结构的平衡，感受到学习新知识的必要性——角的范围扩大了，锐角三角函数也应该“与时俱进”，并不显得突然.把定义的主动权交给学生，引导学生参与定义过程发展思维.）

6.导出任意角的三角函数定义

设α是一个任意角，它的终边与单位圆交于点P（x，y），那么，

y叫做α的正弦，记作sinα，即sinα=y；

x叫做α的余弦，记作cosα，即cosα=x；

yx叫做α的正切，记作tanα，即tanα=yxx≠0.

正弦、余弦、正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们将它们统称为三角函数.使比值有意义的角的集合即为三角函数的定义域.

7.归纳总结，注重渗透

本节课通过对实际问题的解决，学习了任意三角函数的概念.请同学们简要回顾探究过程.三角函数的定义可谓“看似平凡最崎岖.成如容易却艰辛.”（王安石诗）.早期的三角学隶属于天文学，为了天文观测的需要，与古希腊几何有不可分割的联系.尽管三角知识起源较早，但在欧拉以前，人们对三角函数的研究大都在一个半径不定的圆内进行的，运用起来很不方便.直到歐拉时代，才令圆的半径为1，置角于单位圆中，把三角函数定义为相应的线段与圆半径1之比.教材中现在的定义与历史上大数学家欧拉的定义是一致的.欧拉用直角坐标来定义三角函数，彻底解决了三角函数在四个象限中的符号问题，使三角函数成为研究现实世界中周期变化现象的“最有表现力的函数”.

（设计意图：对教学内容进行归纳、疏理、提升.有意加强数学文化的熏陶，让学生在数学学习中寻求数学发展的历史轨迹，感受数学家们严谨治学和锲而不舍的探索创新精神，从而提升自身的文化素养和创新意识.）

【参考文献】

[1]简洪权.高中数学运算能力的组成及培养策略[J].中学数学教学参考，2000.1-2.

[2]张卫国.例谈高考应用题对能力的考查[J].中学数学研究，2001.3.