中国上市商业银行信用风险分析及比较——基于KMV模型及面板数据

李 晟 张宇航

一、引言

商业银行在金融行业内一直扮演着重要的角色，信用风险是商业银行所面临的主要风险之一。相对于外资银行，我国商业银行一直以来都面临着较高的信用风险。以总不良贷款率为例，2015年年末外资银行的平均值只有0.33%，而我国五大行的平均值却高达1.48%。随着近年来我国金融市场的全面开放及自由化，为了适应国际化竞争环境，对于我国商业银行信用风险管理的要求越来越高。因此，采用适当的模型对于商业银行进行信用风险评估及管理就显得十分重要。

据中国银行业监督管理委员会网站于2016年2月公布的数据①数据来源： http： ／／www.cbrc.gov.cn／chinese／home／docView／F9ABBA7979E541568B624CBB3E565AE7.html。，我国商业银行的不良贷款率在2015年第四季度达到1.67%的水平，且这一指标在过去十个季度持续上升。与此同时，关注类贷款和逾期类贷款的增长也相当迅猛，这意味着不良贷款后续仍将面临较大压力。伴随着我国产业结构调整以及经济发展速度的减缓，商业银行势必会暴露在更大的信用风险中，因此能否有效控制与管理信用风险对于整个金融行业甚至整个宏观经济而言都至关重要。

KMV模型是美国KMV公司开发的信用风险量化评估技术，它不仅囊括了历史数据，同时还结合了未来相关数据进行定量分析，因此是国外比较成熟以及常用的信用风险研究方法。本文主要采用这种方法对信用风险进行分析，同时也加入相关数据对于影响商业银行信用风险的特定因素进行实证研究。

本文的主要贡献在于以下几方面：一是采用最新的16家上市银行作为样本，相较于之前的研究有所完善与扩大；二是通过KMV模型得出违约距离的实证结果；三是在第二步之后，接着通过面板数据分析来进一步研究影响违约距离 （即信用风险）的主要因素究竟有哪些。

二、文献综述

（一）信用风险研究的发展历程

有关信用风险的研究经历了从定性、初步定量到精确定量的过程。最初的研究一般采用定性方法，即所谓的专家法 （Foulke， 1961［1］）， 这种方法主要是依赖专家的个人能力对银行及公司信用风险进行评估。但专家法存在一系列缺陷 （Otway和Von Winterfeldt， 1992［2］）， 包括需要依赖风险分析结果来制定行动策略的政策制定者或经理们凭借个人意愿影响分析结果，难以选出正确的专家，难以避免提出错误的分析问题，分析结果可能存在偏误等。

一些研究者选择摒弃专家法转而采用简单的定量分析法研究信用风险 （Beaver， 1966［3］）。 这些专家通过分析企业的利润率、流动资金比率、偿付能力等单一指标来评估其信用风险。简单定性分析法的弱点在于进行这类分析的研究人员并未就哪种指标是最重要的信用风险评估指标达成共识，另外，仅采用单一指标也无法很好地评判企业的信用风险。为了改善采用单一指标衡量信用风险的定性分析方法，Altman（1968）［4］提出了采用Z计分模型对于信用风险进行评估。Z计分模型中包含了运营资本与总资产的比率、未分配盈余与总资产的比率、利息和税前收益比总资产等5个变量。随后Altman等 （1977）［5］又改进了之前的模型，拓展出了ZETA模型，将信用风险评估的变量增加至7个。

然而，简单的定量分析依然难以满足信用风险评估的要求，一些学者进而寻求将不同的模型运用到了信用风险评估当中，例如，Odom和Sharda（1990）［6］、Desai等 （1996）［7］将神经网络技术运用到信用评价之中，建立了神经网络信用评分模型，该模型被证实可以在实践中得到较好的运用。

目前较为流行的模型还有JP摩根银行开发的Credit Metrics模型和瑞士银行开发的Credit Risk＋模型，以及本文中所讨论的KMV模型。Gordy（2000）［8］在文章中对比了由JP摩根银行开发的Credit Metrics模型和瑞士银行开发的Credit Risk＋模型，虽然两者有所区别但是均能解决大体相同的信用风险评估问题。在精确定量信用风险的工具中，由美国KMV公司于1997年建立的KMV模型得到了广泛应用，很多研究都表明KMV模型能够准确地分析信用风险。

（二）KMV模型的应用

因为能对信用风险进行准确预测，近年KMV模型在国内外都得到了大量的应用。Crosbie和Bohn（2003）［9］的研究针对金融类企业，他们发现由KMV模型计算出的金融类企业的预期违约率 （EDF）能够灵敏地反映出企业信用状况的变化。以中小企业为研究样本，Tang（2009）［10］对比了加入违约距离与未加入违约距离的Logistic模型，结果表明包含了违约距离的KMV模型对信用风险的识别效果 （discrimination effect）明显优于其他方法。

在运用KMV模型分析中国上市公司信用风险方面，研究主要集中于分析上市公司违约风险的影响因素。张义强和杨星 （2004）［11］通过研究发现上市公司股价的波动率和预期违约率之间存在显著负相关，而预期违约率可以恰当地反映中国上市公司的信用风险。张泽京等 （2007）［12］分析了中国中小上市公司后发现资产规模对于公司的信用风险有显著的影响，且呈负相关。刘迎春和刘霄 （2011）［13］采用KMV模型可以很好地识别ST公司以及非ST公司之间的信用风险差异，同时还揭示出信用风险在很大程度上取决于公司所隶属的行业。郭立仑 （2012）［14］则比较了ST股票、非ST股票和∗ST股票的信用风险，认为后者的信用风险比前两者都大。高扬敏等 （2009）［15］通过对多家上市公司的面板数据分析发现资产负债率以及资产波动率都与信用风险显著正相关。彭伟 （2012）［16］对于2008年至2011年上市中小企业进行分析，发现其资产规模对于信用风险的影响并不确定且不显著，但是股价的波动是显著和违约距离呈负相关的。凌江怀和刘燕媚 （2013）［17］以10家上市银行作为样本，根据KMV模型得到了违约距离和违约率的实证结果并与标准普尔的权威评级机构进行对比，发现由此得到的结论与评级机构基本一致。

另外一些研究者则致力于对KMV模型的参数估计进行改进和修正，以求模型对信用风险的估计更为准确，这类研究涉及调整模型中的相关参数 （张智梅和章仁俊，2006［18］）或股权价值计算方法 （王建稳和梁彦军，2008［19］），抑或推导出适合中国市场的KMV模型波动率函数 （鲁炜，2003［20］），提出基于CVaR和GARCH （1，1）的KMV模型，以违约距离为基础重新度量信用风险 （王秀国和谢幽篁，2012［21］）， 采用优于 GARCH-KMV 的 SV-KMV 模型（王新翠等， 2013［22］）、 JD-KMV 模型 （谢赤等，2014［23］）。

虽然已有多位研究者采用KMV模型分析了中国上市公司的信用风险，但仅有为数不多的几项研究是采用该模型分析中国银行业的信用风险。谭燕芝和张运东 （2009）［24］基于不良贷款率数据对比了1999年至2007年中美日三国的部分银行，他们发现中国银行信用风险与失业率显著负相关，美国银行信用风险极低且基本不受宏观经济因素影响，但有可能是衍生工具隐藏了这种风险，而日本银行信用风险与CPI呈负相关。Cao等 （2010）［25］主要解决了 KMV模型中违约点的长期负债系数的问题，文章通过信用风险溢价与KMV模型计算出来的违约概率进行对比确定长期负债的最优系数，并将其运用到上市银行分析中。Huang等 （2010）［26］选取了2006年下半年至2008年期间中国银行、中国建设银行以及中国工商银行作为研究对象，计算了三大银行的违约距离并比较了它们的违约率，发现中国建设银行的违约风险高出其他两家银行，而这主要是由于受到其不良贷款率、贷存比以及非利息收入比的影响。

综上所述，虽然采用了较新的KMV模型来评估中国银行业的信用风险，但现有文献依然存在两方面的不足：首先是其研究对象仅涵盖了少数的银行，缺乏对银行业整体的考量；其次，这些文献基本都集中在分析2008年以前的银行数据，而近年来中国宏观经济历经很大的变动，相应的银行监管也有相当程度的变化，过去的研究在一定程度上已难以作为借鉴。我们希望本文的研究有助于弥补这两方面的不足，为银行业监管和风险控制提供更为全面和实时的参考。

三、研究方法

（一）KMV模型概述

1.KMV模型基本原理。

KMV模型由美国的KMV公司于1997年建立并用来估计企业的违约概率。其主要特点是以期权理论作为基础，利用市场上的信息而非简单的历史数据进行预测分析，将不断变动的市场信息纳入违约概率的计算当中，该模型能更准确地反映出企业本身当前的信用情况，比以前的方法有较大突破。

KMV模型主要思路来源于Black-Scholes-Merton期权定价模型 （BS-M Model），即把公司本身的权益部分看作公司资产价值为标的物的一种看涨期权，每当企业借入一笔贷款的时候，就相当于购买了一份以公司资产价值为标的物的以公司负债的账面价值为执行价格的看涨期权，如果负债到期的时候企业资产的市场价值大于负债的账面价值，企业本身就可以执行该期权，偿还到期的债务并获得收益，倘若不执行看涨期权即可认为公司本身资产的价值低于一定的水平，即会产生违约现象，这一水平被称为违约点（Default Point）， 如图1所示。

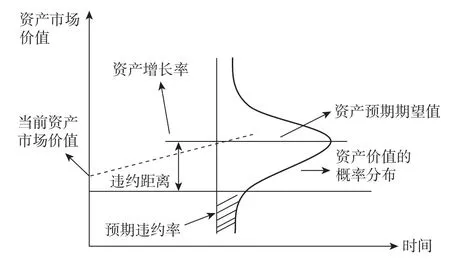
图1 KMV模型原理概述

根据BS-M模型，将其中的变量以上述变量表示，可以得到以公司资产为标的物的看涨期权公式（1） 和 （2）：

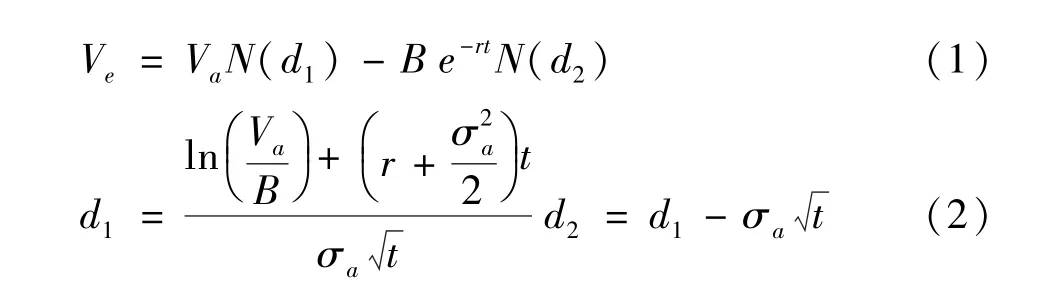
其中，Ve为公司股权市场价值，Va为公司的资产价值，B为负债的账面价值，t为债务的到期时间，r为无风险利率，σe为股权市场价值波动率，σa为公司资产价值波动率，N（·）为标准正态分布累计概率函数。

对于上述公式 （1）进行求导之后可以得出式（3）：

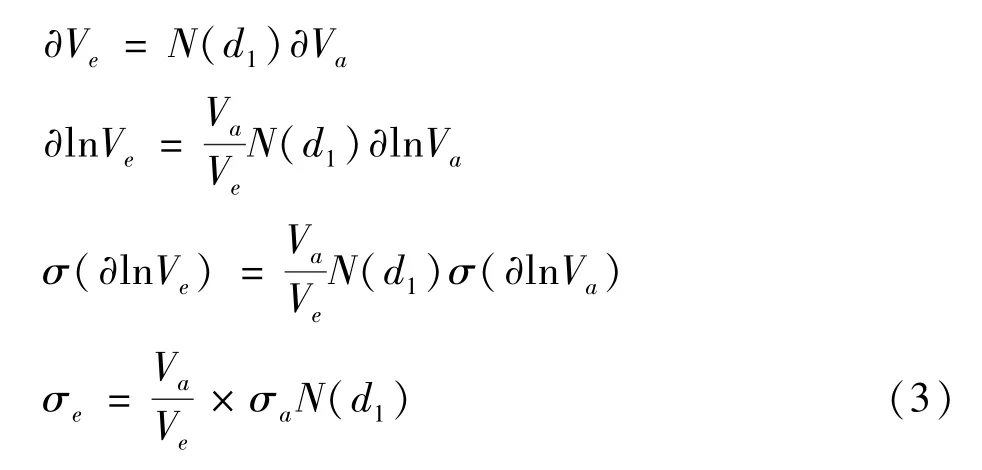
联立公式 （1）和 （3）即可求得资产价值（Va）以及资产价值波动率 （σa）的数值。KMV中定义违约距离 （DD）为

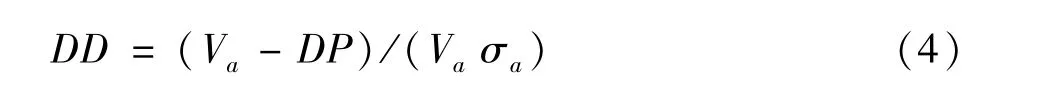
根据上述模型及表达式，本文运用MATLAB软件的相关程序进行方程求解得出结论。

2.KMV模型优缺点分析。

KMV模型的主要优点是：首先，KMV模型可被视为动态模型，主要采用股票市场的数据进行分析，而股市数据几乎是每日更新，KMV模型便可以随着股市的变动而迅速调整；其次，KMV模型带有一定的前瞻性，被认为是面向未来的方法，在一定程度上可以克服那些只是基于历史数据进行分析而产生的弊端。当然，KMV也存在一些弱点：第一，它的主要弱点在于它所需要的假设条件颇为严苛，例如正态分布的假设，就针对公司的研究而言，公司的资产收益分布往往存在 “肥尾”效应，实际情况下很少能满足KMV模型要求正态分布的假设。第二，KMV模型只关注企业的违约预测情况，可能忽略了企业自身信用品质的变化。第三，模型几乎没有考虑到信息不对称下的道德风险问题。第四，必须使用恰当的估计技术来获得公司资产价值、公司资产收益率的期望值和波动率。第五，对于非上市公司来说，由于其自身的资料难以获得或者不够全面，其预测性及预测精度就会较差。

（二）KMV模型变量说明

公式 （1）中的Ve等于股价与总股本相乘的积，其中股价以收盘价来表示，由于BS-M模型中并未包含股利的相关影响，因此在处理股价数据时采用的是复权价格，即不考虑股利发放的最终价格。

无风险利率一般取中国人民银行公布的一年期存款利率①彭伟 （2012）［16］、王建稳和梁彦军 （2008）［19］、王新翠等 （2013）［22］在研究中均选取了一年期存款利率来代表无风险利率。，根据模型需要把相关利率转化为连续复利（表1）。债务到期时间设定为1年。

本文中违约点的设定比较困难。通常KMV模型中将违约点设为短期负债加长期负债的一半，但考虑到我们的研究对象是上市商业银行，在这些银行的历年财务报告中并没有披露其短期与长期负债的数额，而仅仅披露了负债总量以及各负债的明细，我们无法将短期负债与长期负债区分开来，因此，在本文中我们把违约点设定为银行自身负债总额的账面价值。

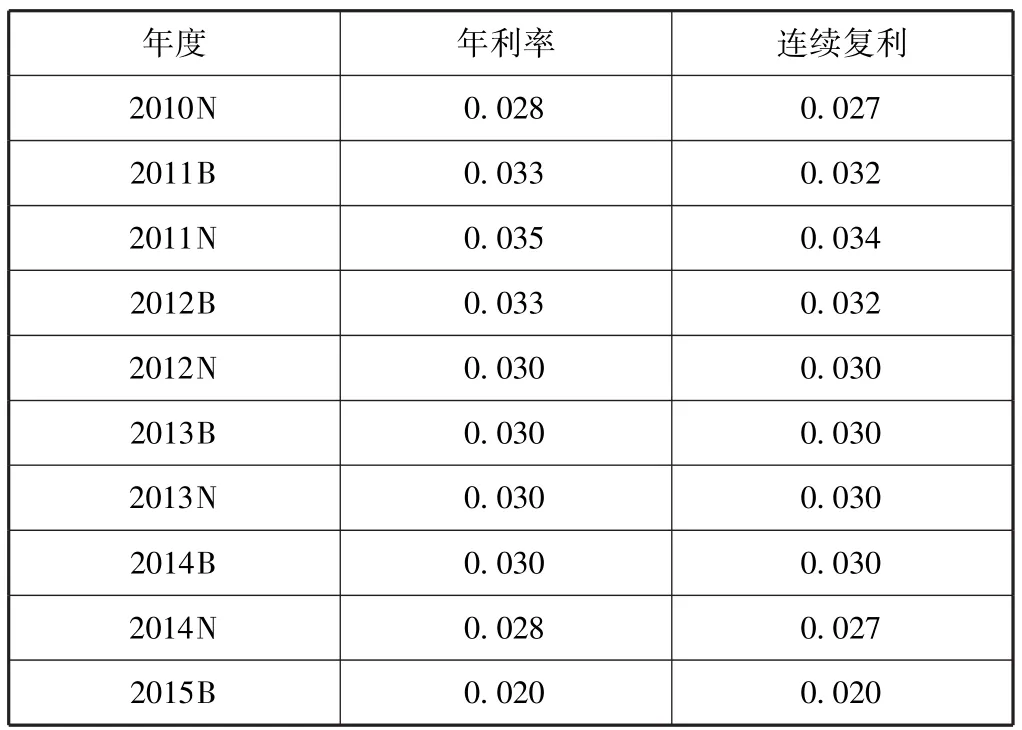
表1 2010—2015年一年期存款利率

（三）面板模型建立

在这项研究中，我们希望计算出16家银行近5年来的违约距离，原始数据属于面板数据，面板模型主要结构如式 （5）所示：

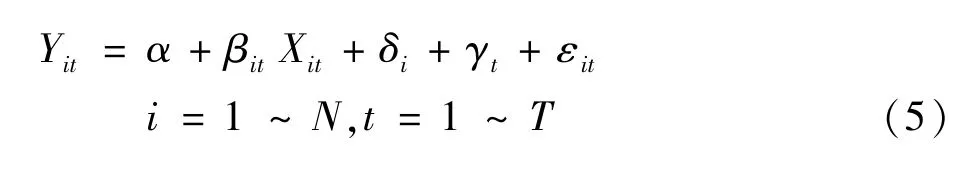
上式的Y代表违约距离DD，i是各家银行，t是不同年份，α为截距项，δi为横截面效应，γt为时间序列效应，εit是误差项。在选择因变量X时，我们参考了分析企业信用风险及银行信用风险的各项研究，最终选取了6个自变量：（1）总不良贷款率 （TNPLR），选取的参数主要借鉴了Huang等 （2010）［26］以及凌江怀和刘燕媚 （2013）［17］的相关研究，我们预期总不良贷款率与违约距离会呈现负相关关系。 （2）总资产（TA）， 根据张泽京等 （2007）［12］及彭伟 （2012）［16］的研究选取这一变量，但是这两篇文章中对于资产规模所得出的结论并不一致，因此对这一变量的研究具有一定意义，由于总资产这一变量数值较大，我们对其进行了对数化处理。（3）贷存比（LDR）， Huang等 （2010）［25］在研究中也选取了这一变量，预期LDR与违约距离呈负相关关系。（4）净资产收益率 （ROE）。（5）资产负债率（D／A）， 前述两个变量均依据Oderda等 （2003）［27］提出的影响银行违约风险的因素而选取的。（6）房地产业贷款占总贷款比率 （RER），这一变量在之前的研究中并未有过深入的讨论，本文之所以加入RER是因为近期房地产业成为焦点，其对于整个经济的作用不言而喻，对于银行就更加重要。本文中的回归方程主要形式如式 （6）：

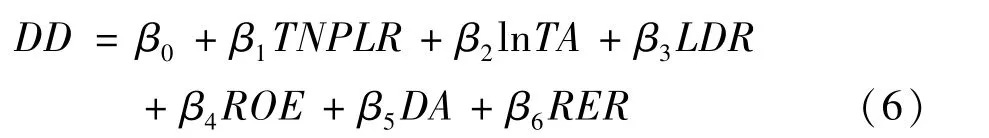
根据上述分析，我们提出如下假设：

H1：总不良贷款率与违约距离呈反比。根据之前的结论可以看出，总不良贷款越多，银行本身的坏账就会越多，这就会造成银行缺乏足够的资金应对其债务，其违约风险就会增加，违约距离就会缩短。

高校食堂是校园生活的重要场所，同时也是食品安全风险隐患突出和事故易发的地方。随着国家政治经济社会的高速发展进步，师生对饮食的要求越来越高，维权意识越来越强，这就要求食堂不断提升质量，确保师生安全用餐。

H2：总资产对于违约距离的影响不确定。但是根据前述研究来看两者可能呈现出正相关关系，即总资产规模与信用风险呈负相关关系，这是由于资产规模较小其本身运营能力及盈利能力就较弱，对于其偿还债务会产生一定负面影响，比之较大规模的银行来看其偿债能力就略有下降。

H3：贷存比与违约距离之间呈现负相关关系。这是由于贷款比例占存款比例过高时，其面对的违约风险可能就更大，更多的贷款可能会收不回来，因此其违约风险就会加大，违约距离就会减少。

H4：净资产收益率与违约距离呈正比关系。净资产收益率越大说明权益本身带来的利润越大，偿还债务也就越有保障，因此违约距离也会加大。

H5：资产负债率与违约距离呈反比关系。资产负债率越高，其偿还债务的比例也就越大，因此其风险也就越高，违约距离就会减小。

H6：房地产业贷款占总贷款比率与违约距离呈反比关系。由于近几年来房地产业库存现象严重，整个行业景气度较低，因此银行贷给房地产业的贷款可能会面临较高风险，因此房地产业贷款比越高，违约距离会减小。

四、数据来源及描述

本文的样本选取了在上海及深圳证券交易所上市的16家商业银行，研究的时间段为2010年12月30日至2015年6月30日，我们选取这段时间的主要原因是：在16家银行中，农业银行和光大银行于2010年下半年才上市，同时所有银行财务报表数据最近更新至2015年上半年。本文每半年计算一次违约距离，以便得到足够数据。所有KMV模型中的数据均来源于WIND数据库，所有面板回归中需要的数据均来源于上市银行的年度与半年度财务报告。数据统计概述如表2所示。

表2 变量统计概述

表3为变量相关系数表。从表3可以看出，各自变量之间的相关系数并不高，相关系数最高的为总不良贷款率与总资产的0.487 2，未超过0.5，因此我们可以认为各变量之间基本不存在多重共线性问题。

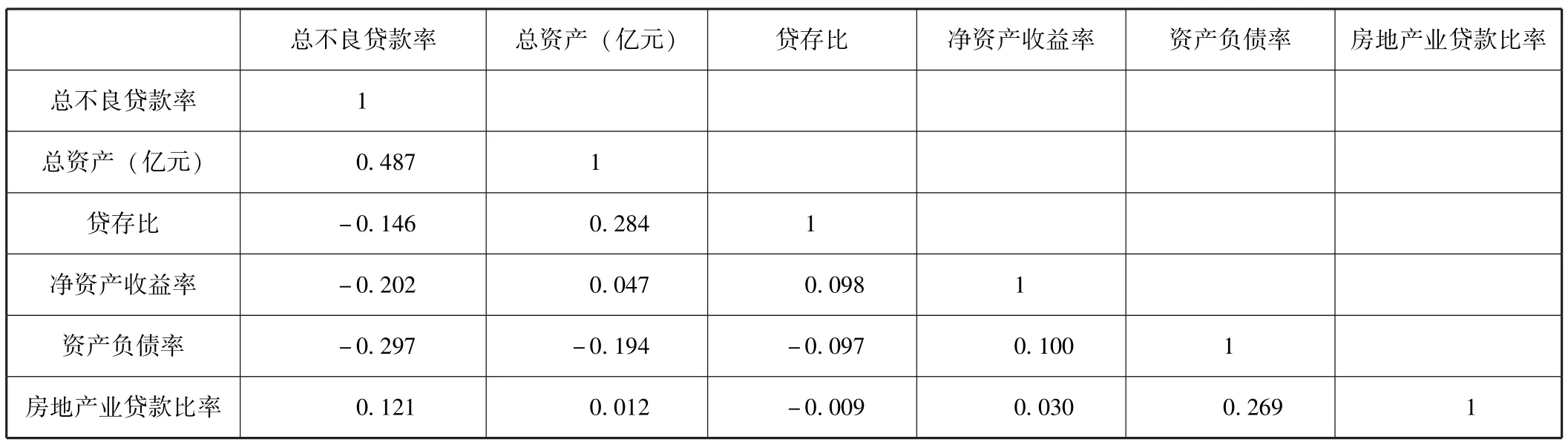
表3 变量相关系数表

五、实证分析

（一）KMV模型结论分析

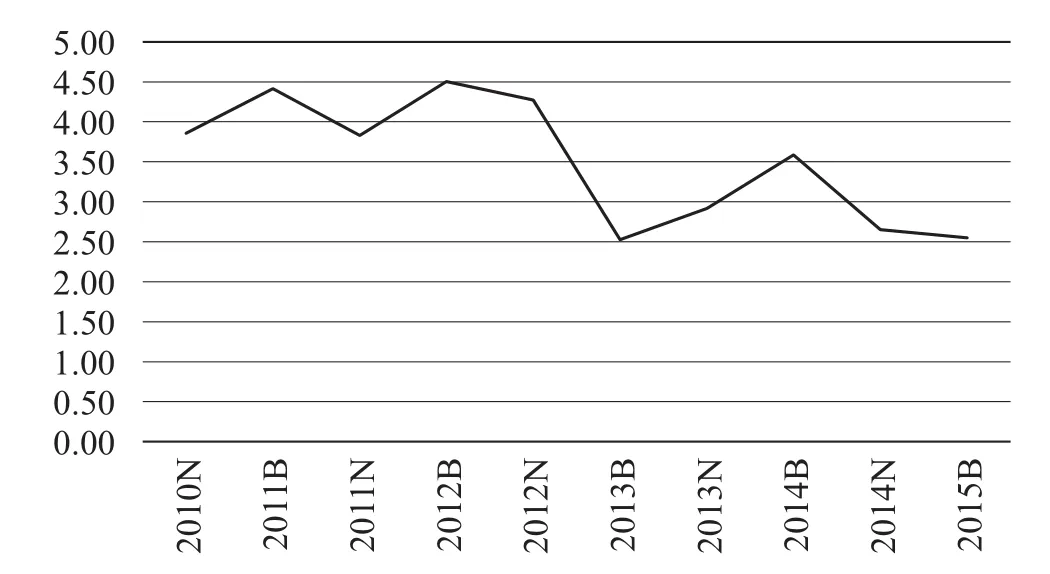
图2 银行平均违约距离时间序列

从图2中可以看到，2014年下半年至今，违约距离有明显的下降，说明在此期间信用风险较高。实际上，在这两段时间内我国整体经济低迷，银行坏账率也相对较高，因此在这期间信用风险会较大，与此同时在最近一段时间内我国经济改革力度加大，股市波动明显表现低迷，对银行业本身也造成了一定的冲击，因此图2与实际情况较为吻合。

为了进一步了解不同所有制如何影响银行信用风险，我们在研究中进一步区分了国有银行 （5家）与非国有银行 （11家）。图3列出了两类不同所有制银行的违约距离平均值。从图3我们可以看出，非国有银行的信用风险要明显高于国有银行，但有趣的是，近年两者的差距急剧减小，在2014年下半年开始几乎趋于一致。这说明近年来政府对银行业的监管力度逐渐增强，对于非国有银行的要求也越来越严格，随着市场逐步开放，非国有银行对于自身的建设以及监管也日益增强，因此国有银行与非国有银行的差距在逐渐缩小中。

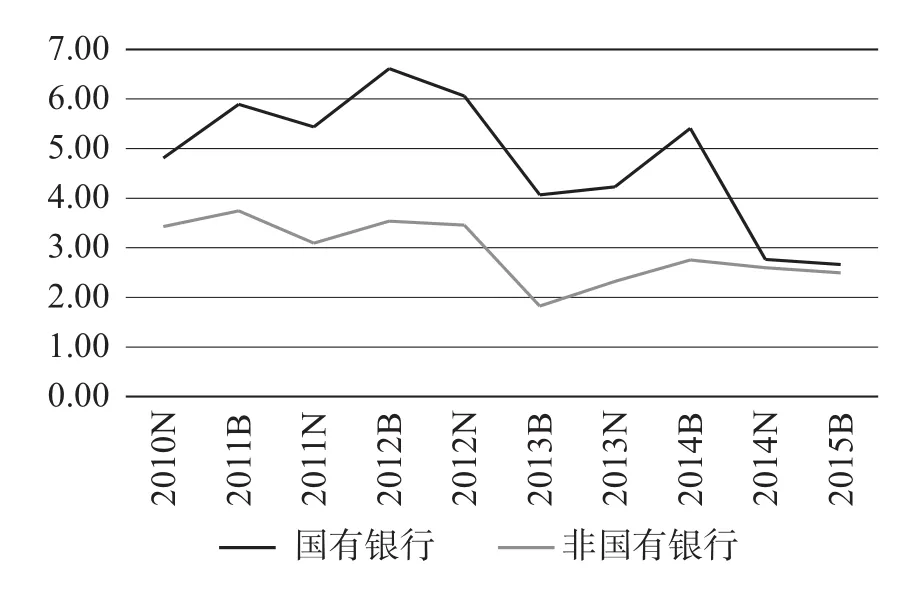
图3 国有银行与非国有银行违约距离对比

（二）面板回归结论分析

根据之前所构建的面板数据模型，我们运用STATA软件对其进行回归分析，其结果如表4、表5所示。

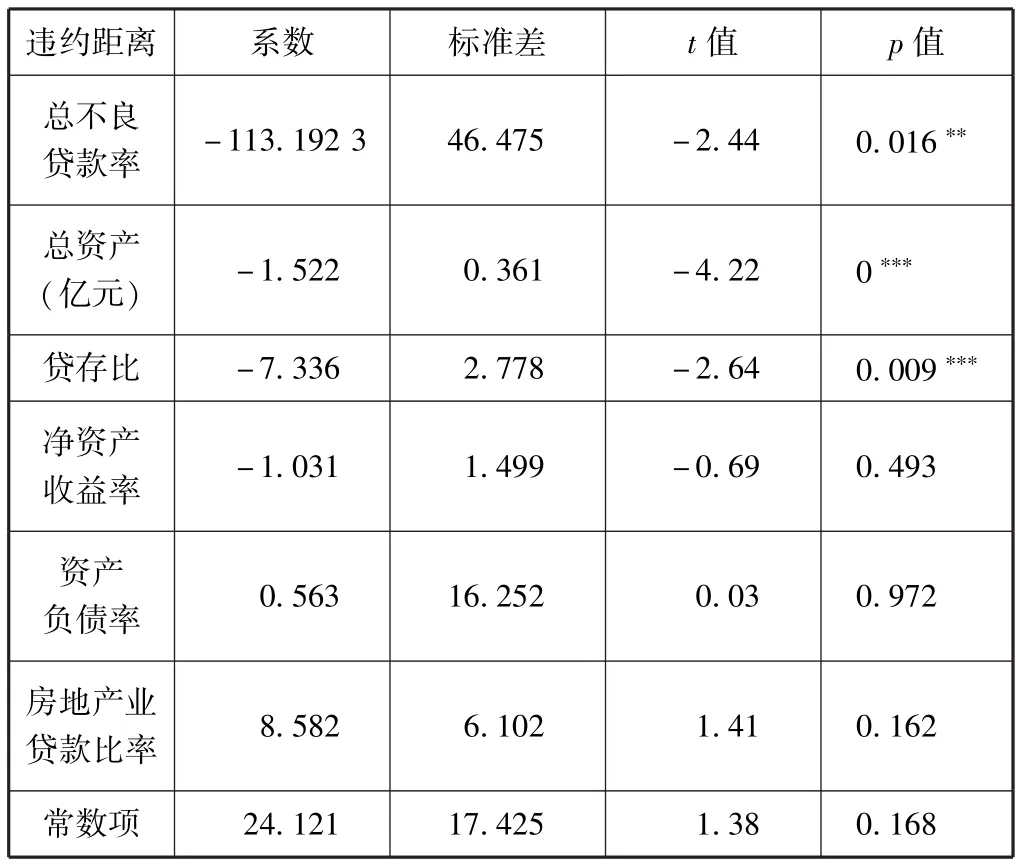
表4 固定效应面板回归结果

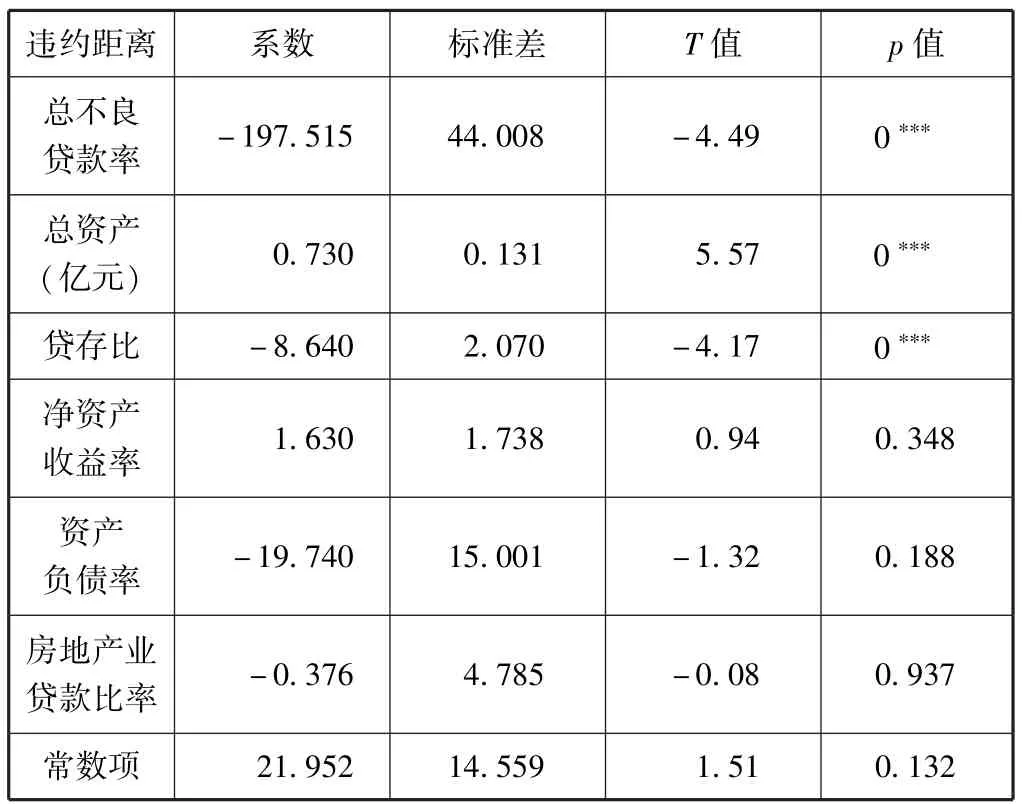
表5 随机效应面板回归结果

根据Hausman检验所得出的结果，其最终的p值为0.976，也就是说Hausman检验未能拒绝原假设，即随机效应模型更为合适，因此在本文中，随机效应模型对于数据来说更加合适。因此，根据表5，我们可以得出式 （7）：

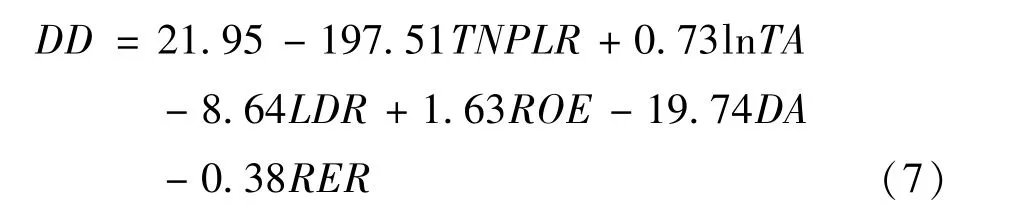
模型的R方为0.344，对于模型而言比较良好，总体的F检验也证明了模型总体较为显著。

在6个自变量中，总不良贷款率、总资产以及贷存比在1%水平上十分显著，其他变量则不显著。这意味着当总不良贷款率上升1%，违约距离会减少1.98；总资产增加1%，违约距离会增加0.73；贷存比每增加1%，违约距离会减少0.86。这些变量的预期符号与我们之前的假设一致。总不良贷款率很高时，意味着银行许多贷款无法收回，银行面临较大流动性问题，过多的贷款不能收回会使得银行自身的信用产生一定问题，对于银行本身的还款能力也会有一定影响，因此违约距离就会降低，违约风险增加。贷存比增加时，贷款比例和数量就会增加，贷款过多也会导致信用风险上升，违约距离下降。而对于总资产而言，资产规模的增加本身可能表明银行的运营良好，具有一定增长前景，规模较大的银行对于风险的承受能力相对较高，因此规模越大风险越低，违约距离也就越大。净资产收益率以及资产负债率均不显著。而房地产业贷款比率之所以不显著，可能是由于其所占比例与规模相较于整体的贷款总数而言还是过小，因此其起到的作用可能并不像预先的那么大。

六、结论与建议

本文通过对我国上市商业银行的分析研究，运用KMV模型以及面板数据作为研究手段，发现相比国有银行而言，非国有银行的信用风险较大，与此同时，受到经济周期等各种宏观因素影响，信用风险的变化与经济的发展变化密切相关。在影响信用风险的诸多因素中，总不良贷款率、银行规模以及贷存比是比较显著的因素。

综上所述，在今后的管理中，非国有银行应该更加注重其信用风险管理，更多地借鉴国有银行的一些管理方法及体系，与此同时所有银行在重视其相关财务数据时，也要密切关注不良贷款率对银行的影响，更加有效地管理其不良贷款，降低信用风险的产生。

［1］Foulke R A.Practical Financial Statement Analysis［M］.5th Ed.New York： McGraw －Hill， 1961.

［2］Otway H， Von Winterfeldt D.Expert Judgment in Risk Analysis and Management： Process， Context， and Pitfalls ［J］.Risk Analysis， 1992， 12（1）：83－93.

［3］Beaver W H.Financial Ratios as Predictors of Failure［J］.Journal of Accounting Research， 1966， 4：71 －111.

［4］Altman E I.Financial Ratios， Discriminant Analysis and the Prediction of Corporate Bankruptcy ［J］.The Journal of Finance， 1968， 23 （4）：589－609.

［5］Altman E I， Haldeman R G， Narayanan P.ZETATM Analysis A New Model to Identify Bankruptcy Risk of Corporations［J］.Journal of Banking and Finance， 1977， 1 （1）：29 －54.

［6］Odom M D， Sharda R.A Neural Network Model for Bankruptcy Prediction［C］.1990 IJCNN International Joint Conference on Neural Networks， San Diego， CA， USA， IEEE.

［7］Desai V S， Crook J N， Overstreet G A.A Comparison of Neural Networks and Linear Scoring Models in the Credit Union Environment［J］.European Journal of Operational Research， 1996， 95 （1）：24－37.

［8］Gordy M B.Comparative Anatomy of Credit Risk Models［J］.Journal of Banking and Finance， 2000， 24： 119 －149.

［9］Crosbie P， Bohn J R.Modeling Default Risk ［R］.White Paper： Moody's KMV Revised December 18， 2003.

［10］Tang Z.The Empirical Study on the Credit Risk Discrimination of Listed SMEs Based on the Distance to Default［C］.2009 6th International Conference on Service Systems and Service Management， Xiamen， IEEE， 2009.

［11］张义强，杨星.我国上市公司信用风险管理实证研究——KMV在信用评估中的作用［J］.经济论坛.2004（1）：43－47.

［12］张泽京，晓红，王傅强.基于KMV模型的我国中小上市公司信用风险研究［J］.财经研究，2007（11）：31－40.

［13］刘迎春，刘霄.基于GARCH波动模型的KMV信用风险度量研究［J］.东北财经大学学报，2011（3）：109－111.

［14］郭立仑.我国上市公司信用风险度量——基于KMV模型［J］.生产力研究，2012（1）：76－81.

［15］高扬敏，陈红伟，陈刚.上市公司信用风险的KMV模型分析［J］.辽宁工程技术大学学报，2009（1）：20－22.

［16］彭伟.基于KMV模型的上市中小企业信贷风险研究［J］.南方金融，2012（3）：23－30.

［17］凌江怀，刘燕媚.基于KMV模型的中国商业银行信用风险实证分析——以10家上市商业银行为例［J］.华南师范大学学报 （社会科学版）， 2013（5）：142－148.

［18］张智梅，章仁俊.KMV模型的改进及对上市公司信用风险的度量［J］.统计与决策，2006（9）：157－160.

［19］王建稳，梁彦军.基于KMV模型的我国上市公司信用风险研究［J］.数学的实践与认识，2008（10）：46－52.

［20］鲁炜，赵恒珩，方兆本，等.KMV模型在公司价值评估中的应用［J］.管理科学，2003，16（3）：30－33.

［21］王秀国，谢幽篁.基于CVaR和GARCH （1，1） 的扩展KMV模型［J］.系统工程，2012（12）：26－32.

［22］王新翠，王雪标，周生宝.基于SV-KMV模型的信用风险度量研究［J］.经济与管理，2013（7）：59－66.

［23］谢赤，赖琼琴，王纲金.基于JD-KMV模型的上市公司信用风险度量——一个区域金融视角下的实证研究［J］.经济地理，2014（6）：137－141.

［24］谭燕芝，张运东.信用风险水平与宏观经济变量的实证研究——基于中国、美国、日本部分银行的比较分析［J］.国际金融研究，2009（4）： 48－56.

［25］Cao Y， Chi G.Dang J.Probability of Default Estimation Model for Listed Bank Based on Minimum Error Management and Service Science（MASS）［C］.2010 International Conference， Wuhan， IEEE.

［26］Huang F， Sheng Y， et al.Evaluation of Default Risk Based on KMV Model for ICBC， CCB and BOC ［J］.International Journal of Economics and Finance， 2010， 2 （1）：72 －80.

［27］Oderda G， Dacorogna M M， Jung T.Credit Risk Models-Do They Deliver Their Promises？ A Quantitative Assessment［J］.Economic Notes，2003， 32 （2）： 177－195.