双电机机构协调运行的研究

梁保家

（广东科学技术职业学院工业中心，广东 广州 510640）

双电机机构协调运行的研究

梁保家

（广东科学技术职业学院工业中心，广东 广州 510640）

在起重、运输生产中经常遇到由于双电机机构运行不同步而造成严重的生产事故，为了使双电机机构能够达到自动同步的良好状态，采用了双电机机构协调运行的最优控制方法，通过变频调速、PLC和上位机相结合，实现了双电机机构的自动同步.通过计算机仿真结果验证了这一方法的优良效果.

自动控制；最优控制算法；误差变量法；定常无限时间状态；正定阵

在工业生产中，经常遇到双电机机构协调运行的问题，例如多用途起重机在进行吊钩、抓斗、集装箱等生产作业时，如果双电机不能协调运行，则会造成严重的生产事故.自从 Koren［1］在1980年提出交耦控制器后，多机协调控制理论开始深入到速度和转角双重同步的协调控制.近年来，运用现代控制理论的控制方法，把鲁棒控制、模型参考自适应控制、神经网络与遗传算法等应用到多电机协调控制中，取得了很好的效果.

本文以多用途起重机进行吊钩、抓斗作业时的运行状况为例进行分析，设计出简单易行、有实际应用价值的双电机同步控制系统.

1 工作原理

双电机协调运行的原理基于简单的闭环控制，首先对两台电机转速或转角变化进行检测，并把两台电机所产生的误差量反馈给上位机，经过上位机最优控制算法，再输入变频器，由变频器调节电机的速度而达到双电机同步运行［2，3］.

图1.1为起重机电机机构控制图.该系统在起重机电机上装有编码器，编码器的脉冲反映了电动机的即时运行状态（速度和转角），并输出至 PLC计数模块.如果把上述电机机构控制系统同样安装在 2台电动机上，那么当 2台电动机的运行状态发生不协调，即速度或转角产生误差时，两个编码器的脉冲数就会产生误差，此误差经过 PLC计数模块分辨后输入上位机，再由上位机采用最优控制算法得出最佳控制量，并把信号输出至PLC，PLC对变频调速器进行控制，最终使 2台电机的运行状态完全同步.

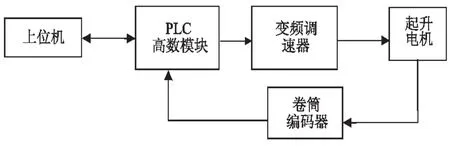
图1 .1 起重机电机机构控制图

显然，该系统中的关键因素是上位机的控制算法，双电机机构能否同步运行取决于其控制算法的优越性.现在首先对单台起重机电机进行数学分析［4］，如图 1.2所示.

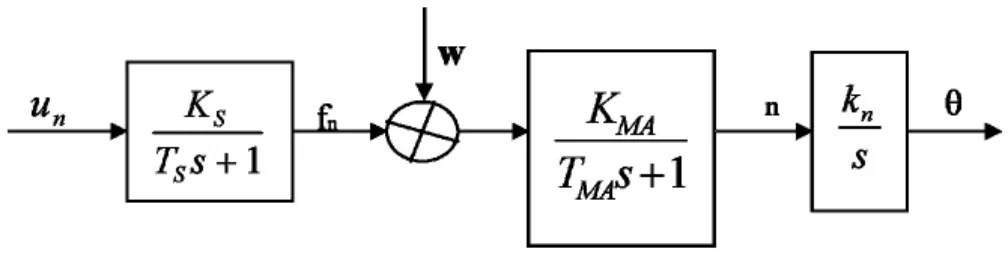
图1 .2 单台起重机电机数学模型分析

图1.2中，起重机电机的输入量为频率 f，输出量为转速 n，这是一个单变量环节，图中的 un是控制变频器的电压矢量.当起重机电机为全电压起动时，其数学分析模型为

式(1.1)中，TMA是惯性时间常数，设电机的启动时间为 tq，如果假设启动过程在 4TMA时结束，可得 TMA=tq/4；KMA为输入频率 f与输出稳态转速 n之比.对于变频调速的起重电机，在直接启动时，考虑到滞后作用，变频器的数学模型可看成是一个惯性环节：

上式(1.2)中，Ks是外加模拟电压与变频器设定频率的比值；Ts称为变频器的惯性时间常数，可以通过升速时间 tq来计算.升速时间 tq是变频器由最低频率 fs升高到最高频率 fh所用的时间，由于交流电机的最高频率为 50Hz，所以实际的升速时间是

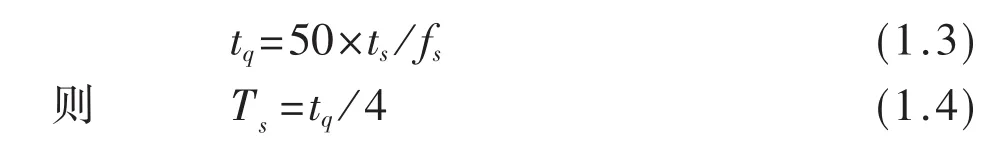
2 最优二次型控制方式

最优二次型控制方式是现代控制理论及其应用领域中最富有成果的一部分.最优二次型不但性能指标具有鲜明的物理意义，而且可以兼顾系统性能指标的多方面因素，例如快速性、能量消耗、准确性、灵敏度和稳定性［5］.考虑到工程上的实用价值，本文采用最优二次型控制方式中的定常无限时间状态调节器，在建立其系统状态方程时必须考虑到在实际生产中外部扰动是不可避免的，设其状态方程为：

式(2.1)中 W（t）是扰动变量，其性能指标如下：

其最优控制状态可表达为

式(2.3)中：P为正定阵，满足下式

对于定常无限时间状态调节器，在有恒定的外部扰动输入时，当 t→∞ 时，x（t）并不为 0，而是趋近于某一稳态值，因此式(2.3)中 u（t）也将不趋于 0，式(2.2)的性能指标 J[u（t）]将是发散的，这就导致式(2.1)失去其最优性.为此，在实际系统有恒定的外部扰动输入时，采用误差变量法，引入包含着与外部扰动量有关的偏差形式的状态变量，这样，在有恒定的外部扰动输入时定常无限时间状态调节器仍然能够保持其最优的性能指标.采用误差变量法，引入包含着与外部扰动量有关的偏差形式的状态变量，此时调节器的稳定状态为：

上式（2.5）中，xs，ys分别为x（t），y（t）的稳态值.

将式(2.5)代人(2.1)，可以得到稳态表达式

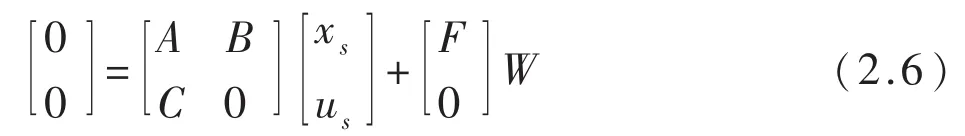
上式（2.6）中，us是u（t）的稳态值，由上式得

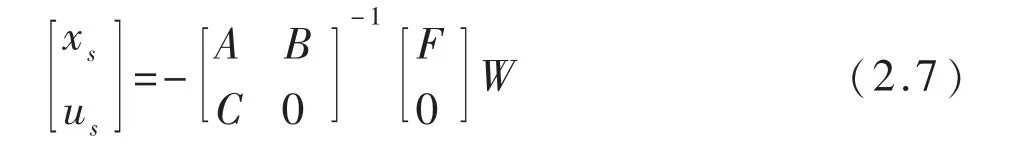
现在的问题转化为在式 (2.9)的约束条件下，求取二次型性能的指标 J[ue（t）]的最小值.

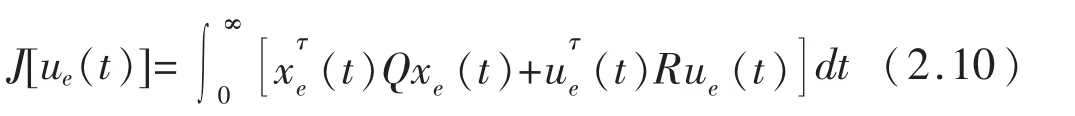
由式（2.13）可见，最优控制包括了状态反馈-R-1BτPx（t）和按扰动补偿的前馈 HW（t）.

3 双电机协调的最优控制算法

根据以上分析，可以确定双电机协调运行的最优控制模型［6］，见图 3.1.

图3 .1 双电机协调运行的最优控制模型

上述模型中的输出量 e是位置偏差，理论要求 e=0，θ1，θ2分别为两台电机的位移 (转角)，输出量 x1=θ1-θ2；n1，n2分别为两台电机的转速，这里设 x2=n1，x4=n2；fn1，fn2为两台变频器输出的频率，令 x3=fn1，x5=fn2；W1，W2为负载干扰量.

根据结构图可列出如下状态方程

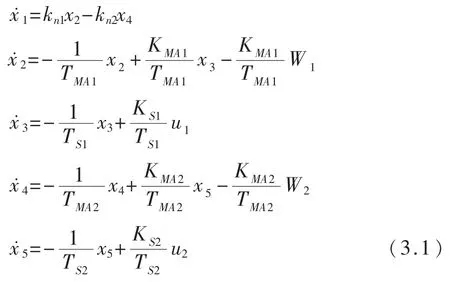
写成矩阵形式

应用误差变量法，系统的最优控制为

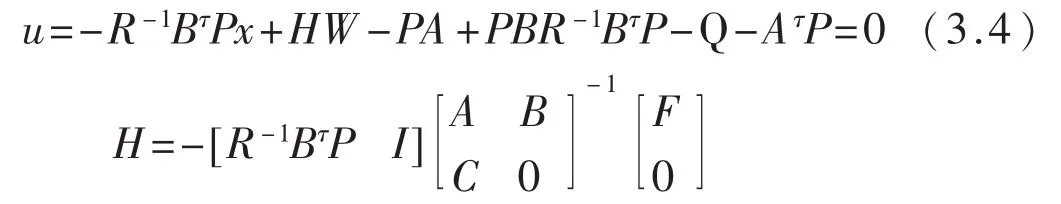
在上位机的程序设计中可植入上述算法，用以对电机进行自动协调控制.

4 计算机仿真

由以上分析可得出该最优控制模型的各项参数如下：

1)起重机电机在工频全电压起动时，可测得tq=0.85s

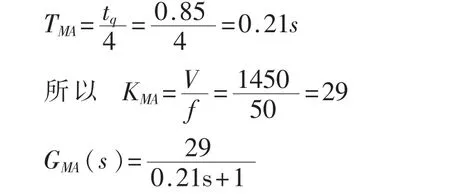
2)变频器 设定实际加速时间为1s

3）积分环节 根据角速度与角度的单位换算关系得

再由以上参数计算出A，B，F阵

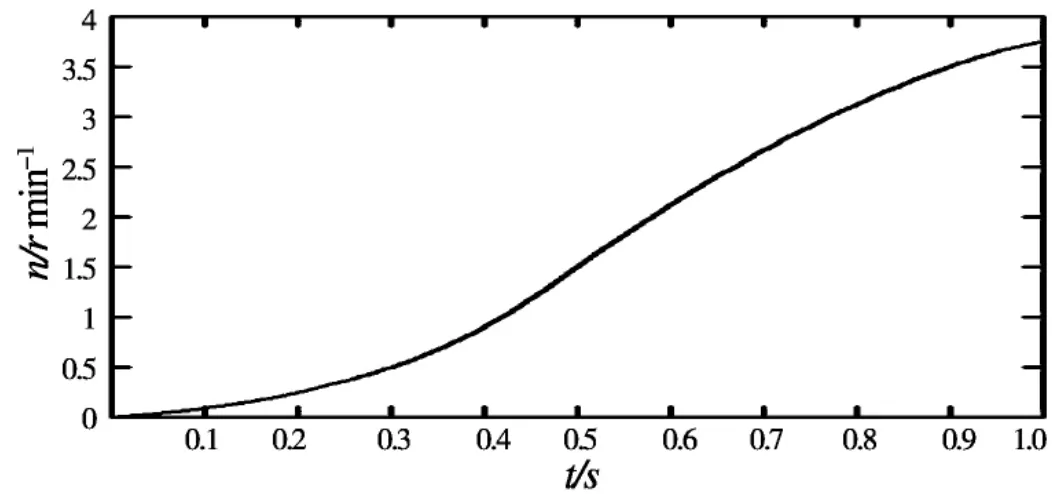
图4 .1 原始系统的动态仿真图

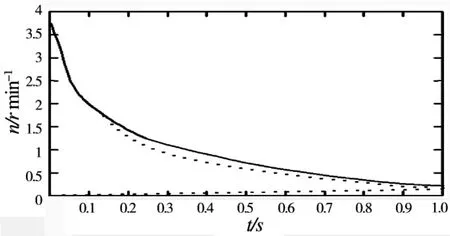
图4 .2 加入最优调节的动态仿真图

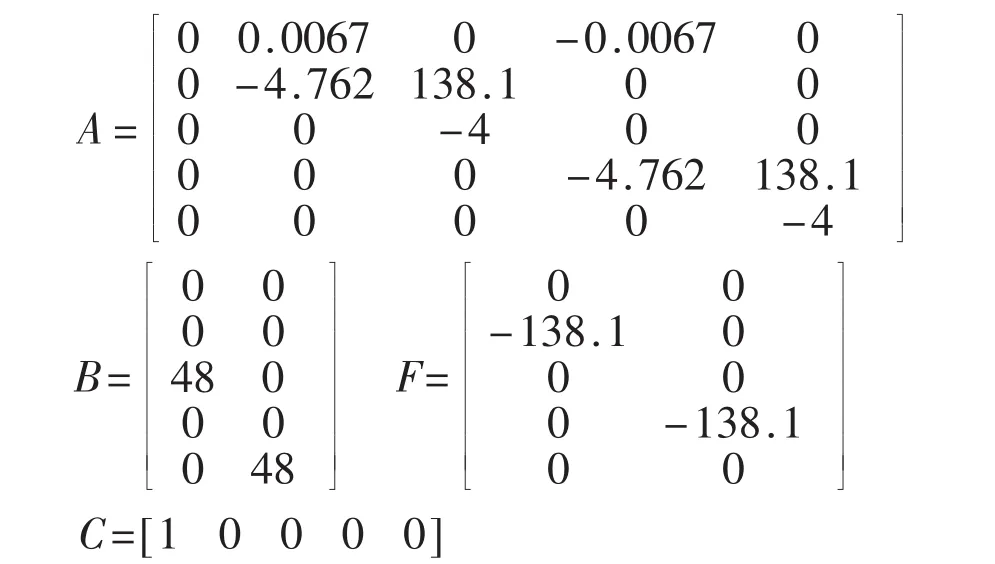
在式(3.4)中可以看到参数对于最优调节器起到关键的作用.该最优控制模型的准确程度，可通过MATLAB对其进行仿真［5］.

图4.1为原始系统的动态仿真图，1s之内的角位移为 3.77r，图 4.2为加入最优调节后，1s之内的角位移降低为 3.318×10-6r，计算机动态仿真结果证明加入最优调节后的性能指标有了极大的提高.

5 结论

上述分析和仿真结果都充分说明，这种定常无限时间状态调节器的设计方法是可行的，有实际应用价值，不仅能够快速纠正双电机之间的误差，实现精确的同步跟踪，而且对外部干扰具有很强的鲁棒性.该控制器能否应用于更加广泛的场合，还有待于进一步研究.

［1］Koren Y.Cross.coupled biaxial computer control for manufaeturing system ［J］.ASME Journal of Dynamic Systems，Measulment and Control，1980，102(12)：256—272.

［2］孙文焕.多电机协调控制的发展 ［J］.电气传动，1999，6：3～6.

［3］何济民.转速闭环变频调速系统的建模与调节器参数设计.电气传动自动化，2000(2)：34～38

［4］Pradeep A K.Shruz S M.A control law that itehieves simultaneous tracking for a group of system in finite timelJJ. ASNE Journal of Dynamic Systems，Measurement and Contml，1992，114(4)：140-148.

［5］胡中楫.邹伯敏，林冬青等.最优控制原理及应用.杭州：浙江大学出版社，1988.126～188.

［6］易灵芝,朱建林,张林亭,李卫平.最小二次型(LQ)控制器的工程化最优设计［J］.兵工自动化,2001年03期.

［7］薛定宇.控制系统计算机辅助仿真 ［M］.北京：清华大学出版社，2000.

［责任编辑：王晓军］

Study of Coordinated Operation about Bi-motor

LIANG Baojia
(Guangdong institute of science and technology,Guangzhou 510640，China)

Serious production and safety issues are caused in industrial due to dissonance operation of double-motor mechanism.In order to solve this problem,the theoretical analysis is carried out.Depending on optimal control scheme，with the ideal result of Double motor automatically synchronized is achieved by combining.At the same time the computer simulation result shows its excellence.

automatic control;optimal control algorithm;constant infinite time state;positively definite matrix

U 653．921

A

1672-402X（2016）08-0053-04

2016-01-20

广东省科技厅项目：广东创意人才库公共服务平台建设（粤科规财字【2014】116号 2013B040405006）,基于广东产业转型升级的创意产业公共信息服务平台建设（粤科规划字【2012】98号 2012B040306005），学校项目：“开关电源示教板”的开发与研制.

梁保家（1977-），男，广东阳江人，广东科学技术职业学院工业中心实验师，研究方向：计算机通信与电磁兼容.