基于k-means聚类和BP神经网络组合模型的用电负荷预测

黄　磊，陈　浩，衣乔木，陶亚龙

(1.上海新能凯博实业有限公司，上海　201210；2. 复旦大学计算机科学技术学院，上海　201203；3. 网络信息安全审计与监控教育部工程研究中心，上海　200203)

基于k-means聚类和BP神经网络组合模型的用电负荷预测

黄磊1，陈浩2,3，衣乔木1，陶亚龙1

(1.上海新能凯博实业有限公司，上海201210；2. 复旦大学计算机科学技术学院，上海201203；3. 网络信息安全审计与监控教育部工程研究中心，上海200203)

摘要：电能资源不能存储，节约电能的一个重要前提就是精准预测用电负荷。由于居民的用电负荷受多方面因素的影响(如天气)，使得用电负荷曲线为高度非线性曲线，但用电负荷的曲线又具有周期性，对于建立这种高度非线性函数并具有一定的周期性的预测模型，神经网络是一种非常合适的方法。针对现有的电力数据，并参考了现有的方法，提出了k-means聚类和BP神经网络组合模型的预测方法来预测用电负荷，通过与单独使用BP网络预测的结果进行对比，认为使用k-means聚类和BP网络的组合模型方法进行用电负荷预测，可获得较高精度。

关键词：用电负荷；天气；k-means聚类；BP网络

电力是现代工业发展的根本，也是我国的重要资源。为了更好地利用电能，上海市从2012年7月1日起，实施居民阶梯电价，其目的是为了促进居民合理用电，节约用电。由于我国的智能电网的发展技术相对于欧美、日本要滞后许多，导致了我国多次的用电供需失衡。国家为了解决供电量不足的问题，鼓励各地的发电厂大力发电，同时，也导致了很多地区用电量过剩，对电力资源造成了极大的浪费。因此，用电量预测已经成为了电力部门的一个重要组成部分，寻找准确科学的预测方法是当前的首要任务。

用电负荷预测并不是一个新颖话题，该理论研究开始于20世纪80年代，到目前为止，已有30多年的历史。在此期间，有许多的理论和方法被提出，甚至有些已经被实践，应用到实际中去，可是，效果并不尽人意。不同的预测方法都有一定的局限性，至今，还没有一个预测方法是普适的、是绝对的最优解。虽然用电负荷的预测方法有很多，但从大方向来说，可将其分为传统的预测方法和经典预测方法[1-2]。无论哪种方法，都已其明显的缺点。

常用的传统预测的方法有相似日预测法和卡尔曼滤波理论预测法。其缺点在于难以对噪声的特性经行估算。

常用的经典预测方法有时间序列法和回归分析法[3]。时间序列法的缺点是他只注重数据的拟合，没有充分的考虑影响负荷变化的原因有哪些。回归分析法的缺点是在使用时需要实现假定函数的基本形式，并且也不能真实的反映出负荷与影响因素之间的关系[4]。

近些年来，随着人工智能的兴起和不断发展，在很多领域中得到了广泛的应用。其中，人工神经网络具有非线性特性和较强的学习和归纳能力，同时可以充分考虑影响负荷变化的外部因素，从某种程度上，可以克服以上预测方法的不足。正是因为这样，神经网络在用电负荷预测的研究中，广受亲睐。由于数据量之大，单纯的用神经网络可能达不到理想效果，在建立神经网络之前，有必要对数据进行处理。在本文，使用k-means聚类方法，对数据进行归来，然后再建立BP网络预测模型，对用电负荷进行预测。

1数据处理及分析

1.1实验数据来源及处理

本论文的所用的用电负荷数据是上海浦东2013年1月1日至2013年12月31日的真实数据，来源于2013年数据来自浦东电力局。由于2013年的原始数据记录信息不完整、数据记录错误等原因以及数据采集的所造成的错误，造成一部分用户没有完整的365天的用电信息和一部分用户用电量为负值的情况，无法进行统计；因此，有必要对原始数据进行筛选和预处理操作。将没有完整2013年365天数据记录的居民用户和用电量为负值的居民用户剔除，最后得到了5 036户居民用电数据。为方便观察，将5 036户居民2013年1月1日至2013年12月31日的用电总量拟合成折线图，如图1所示。

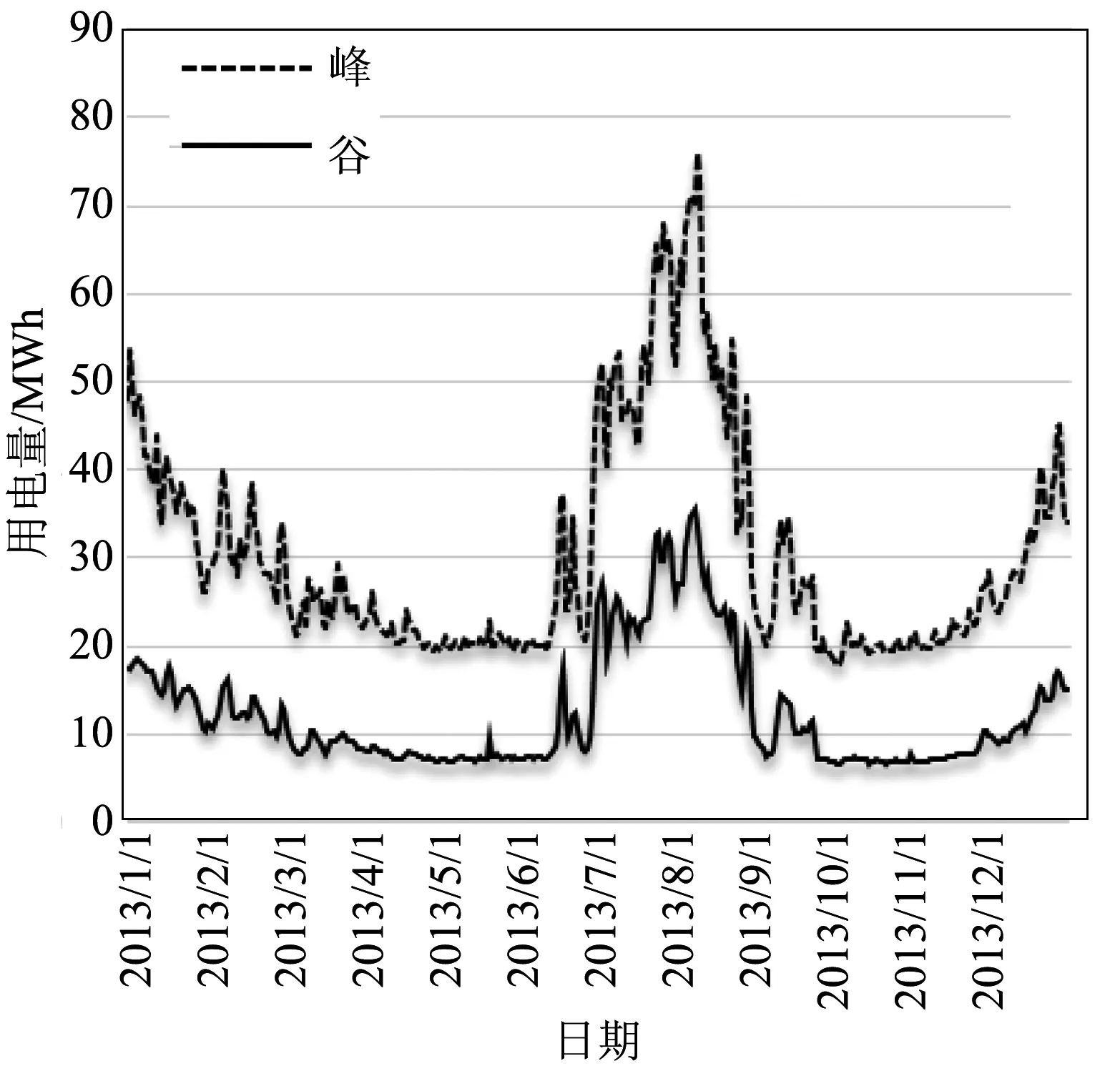
图1　居民用电量

此外，由于居民用电负荷还与环境因素有关，比如温度。本文也是重点考虑温度对用电负荷的影响，所以，还要获取2013年1月1日至2013年12月31日的天气数据。本文所使用的天气数据，是来自于上海浦东国际机场的所使用的天气数据。

1.2实验数据分析

由图1可以看出，用电量在7月至9月为最大，而且波动也较大，1月和12月次之，4月至6月和10月至11月，用电量最小，而且也相对稳定。其原因也不难理解，由于7月至9月处于高温时段，制冷设备会大量使用，1月和12月为最冷时段，供热设备会大量使用，所以，会消耗更多的电量，导致用电量最大。而4月至6月，10月至11月时，在上海温度比较适宜，大功率的制冷供热设备较少使用，所以其用电量为最少。从以上的结论也可以看出，温度高或者温度低时，用电量会增大，这一结论也符合我们的常识。

此外，用电负荷曲线为光滑连续曲线，且日用电负荷也会呈现一定的周期性，所以，前一天的用电负荷，对预测当日的用电负荷具有一定的参考意义[5]。

2K-means聚类和BP神经网络在用电负荷预测中的应用

2.1聚类分析

在数据挖掘领域中，聚类方法有多种，例如：K-means、k-中心、层次聚类、基于密度的聚类等等。由于K-means算法简洁、快速、聚类结果比较理想，因此，K-means聚类方法也得到了广泛的应用，本文也是采用的是K-means聚类。

K-means是典型的划分聚类方法。将数据集D划分成K个类。需要定义簇的代表：形心。从几何概念上来讲，簇的中心点就是它的形心，而在这里，形心可以有更多的定义方式，不仅仅是中心点，还包括了均值等。评估簇的质量可以用误差平方和，它的定义如下：

(1)

式中E——的数据集所有对象的误差的平方和；

p——空间上给定数据对象的点；

dist(x,y)——空间上点x到点y的欧几里得距离。

接下来，要讨论的是k是如何取值的。找到合适的k值，并非一件容易的事情，k的取值，对聚类的结果有着不同的影响。通常，找出正确的簇数依赖于数据集分布。在这里，采用肘方法，来确定k的取值[5,6]。

肘方法是基于如下观察：增加簇的数有助于降低每个簇的簇内方差之和。这是因为有更多的簇可以捕获更细的数据对象簇，簇中对象之间更为相似。因此，一种选择正确的簇数的启发方式是，使用簇内方差和关于簇数的曲线拐点。

2.2聚类过程及结果

在本文，我们根据每个用户每个月的用电总量，进行聚类，这样可以得到5 603*12的二维向量，根据上述论述的肘方法，得知k为3时，为最佳簇数。将每个用户，按每月用电总量进行分类，分为三类：低用电量用户、中用电量用户、高用电量用户。

根据以上的运算过程，可以得到用户电量的聚类的结果，观察簇心的分布情况如表1所示。

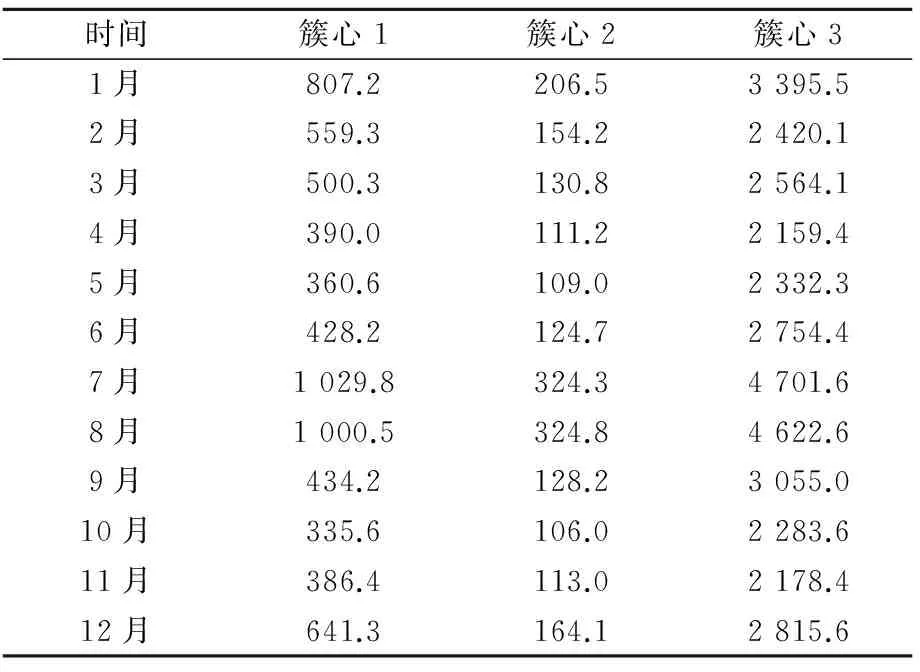
表1　用户用电量聚类结果的簇中心　kWh

2.3BP网络模型的建立

2.3.1BP神经网络

人工神经网络有很多种，如，BP神经网络，径向基神经网络，递归网络等。人工神经网络提供了普遍而使用的方法。对于建立高度分线性的模型函数提供了一种非常健壮的方法。在众多的神经网络当中，由于BP网络，非线性映射能力，自学习、自适应和容错性强的特点，使得BP神经网络得到了广泛的应用。其结构见图2。

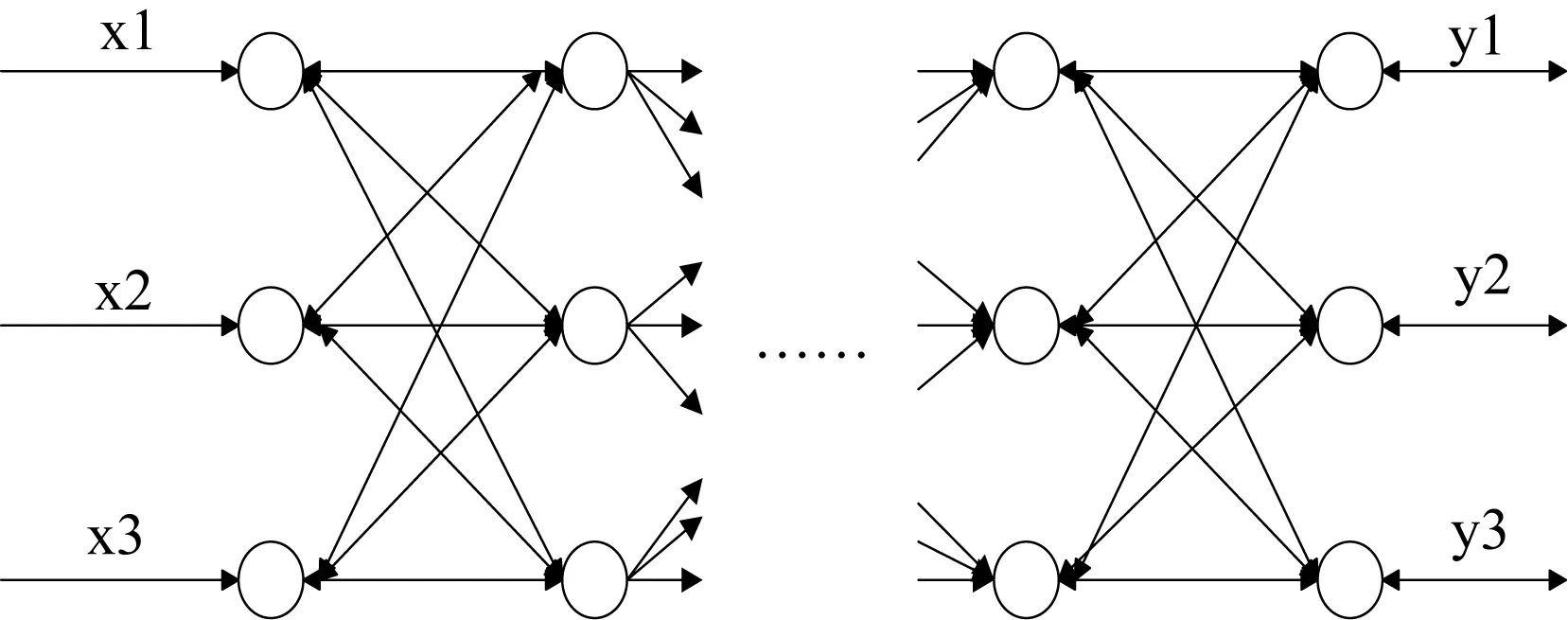
图2　BP网络结构

2.3.2输入/输出向量设计

输入向量就是一天峰时用电总量的真实值、谷时用电总量的真实值及当天的最高气温和最低气温。因此输入向量就是一个8维向量(前一日峰时用电量，前一日谷时用电量，前一日用电总量，当日峰时用电量，当日谷时用电量，当日用电总量，最高气温，最低气温)。

显而易见，目标向量就是当天的峰时用电量和谷时用电量，(当日峰时用电量，当日谷时用电量)[7]。

由于输入/输出向量的值比较大，也比较分散，而且数量级差异也较大，预测起来会产生很大的误差，因此还需要对输入/输出向量进行归一化处理，由于输入/输出向量的每列的数值相差很大，所以，需要单独对每一列归一化，使每列数值处在[0，1]范围之间，然后再重新组合成输入/输出向量矩阵。测试后的结果，要进行反归一化。归一化的方法有很多，这里采用如下公式[8]：

(2)

2.3.3BP网络设计及训练

由于本论文的用电量预测输入向量是一个8维向量，根据Kolmogorov定理可知，中间隐含层的神经元可以取10。而输出向量有2个，所以输出层中的神经元应该有2个。在本文用matalb来实现该过程，网络中间层的神经元传递函数采用S型正切函数tansig，输出层中的神经元传递函数采用S型对数函数logsig。这是因为函数的输出位于区间[0，1]中，正好满足网络输出的要求[9-11]。

利用以下代码在Matlab上创建一个满足上述要求的BP网络：

net=newff(minmax(sd),[8,2],{'tansig',logsig},'traingdm')；

其中，变量minmax(sd) 用于规定输入向量的最大值和最小值，traingdm表示设定网络训练函数为traingdm，它采用Levenberg-Marquardt算法进行网络学习。

网络设计好之后，还要进行网络训练，网络经过训练后才可以用于用电量预测的实际应用(见表2)。

表2　参数训练

训练代码如下：

net.trainParam.lr= 0.05; %学习速率

net.trainParam.epochs= 10000; %训练次数

net.trainParam.goal= 1e-3; %训练目标

3实验结果

3.1BP网络预测结果

训练好的模型还需要进行大量的测试才可以判断是否可以投入实际应用。利用以上方法，分别将三类用户按照上述方法建立模型，并且也分别得出了三类用户用电量的预测结果，将所得的三类用户用电量的预测结果，进行汇总，可得到以下结果。

单独使用BP神经网络预测所得到的结果以及相对误差绝对值和分布情况(见图3、图4)。

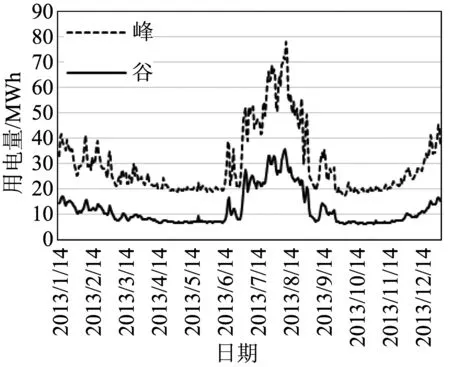
图3　BP网络预测结果

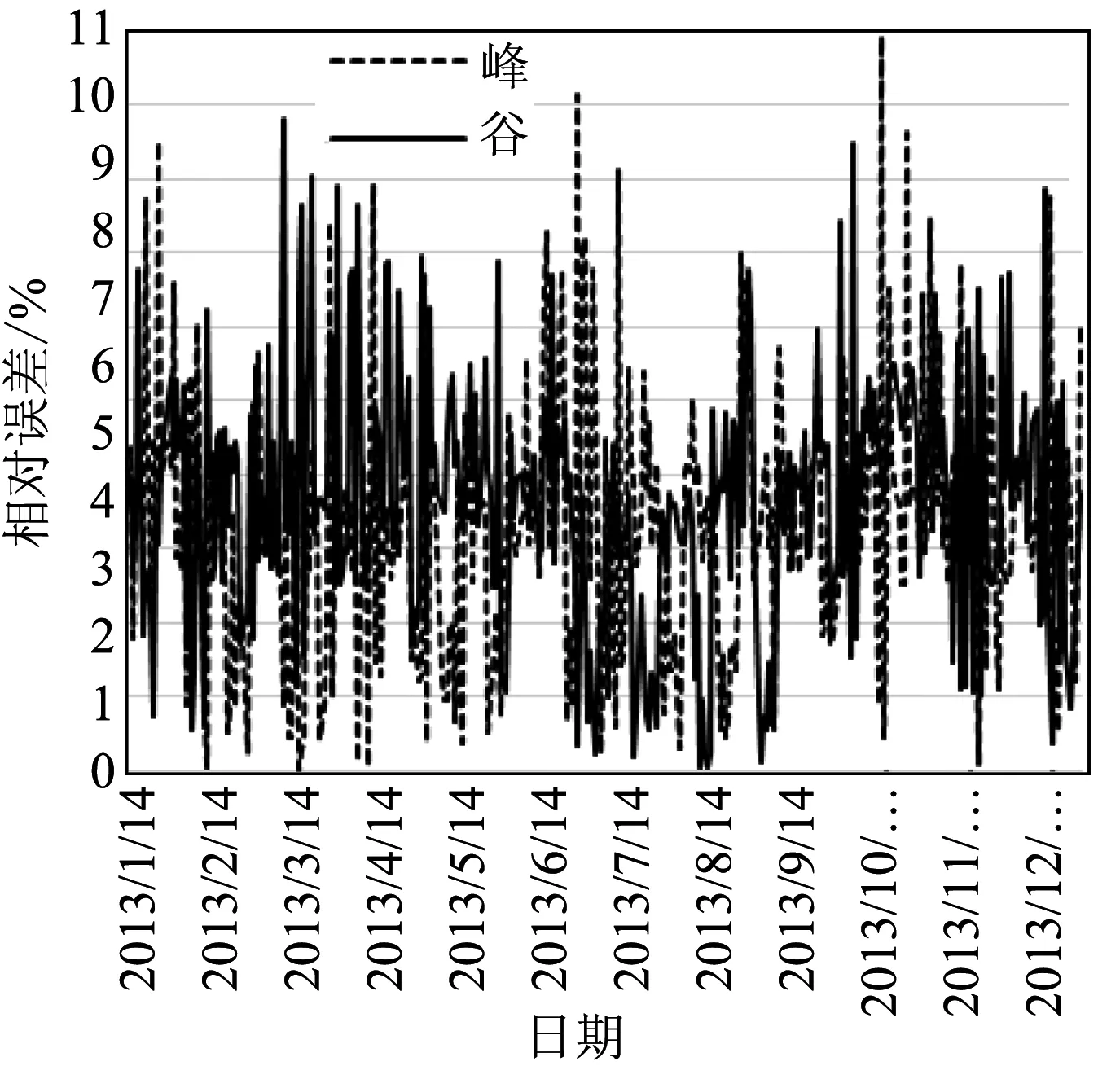
图4　BP网络预测结果相对误差值

3.2k-means聚类和BP网络组合的预测结果

基于k-means和BP网络组合的预测结果如图5所示。

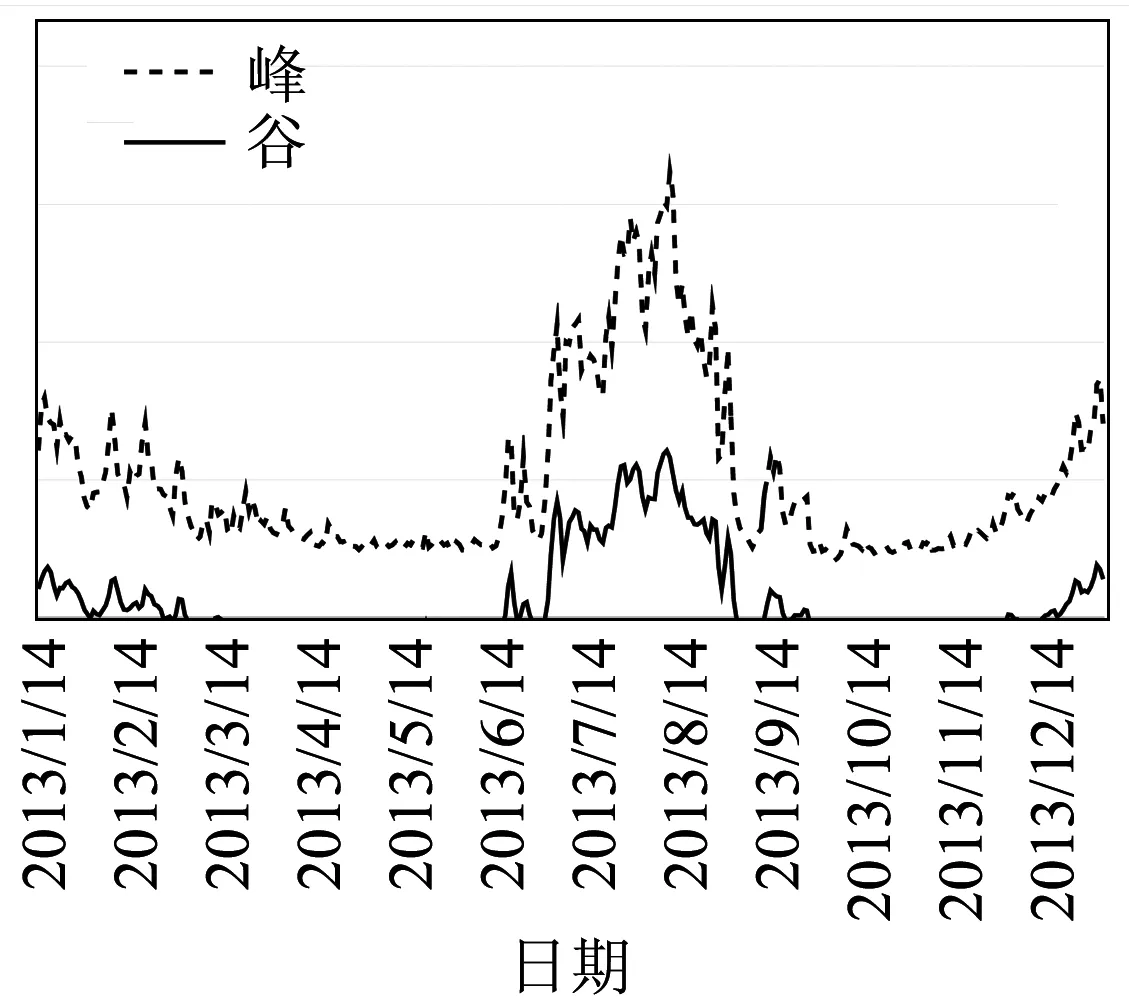
图5　基于k-means和BP网络组合的预测结果

将误差值除以用电量的真实值，可得到相对误差绝对值，绘出曲线如图6所示。

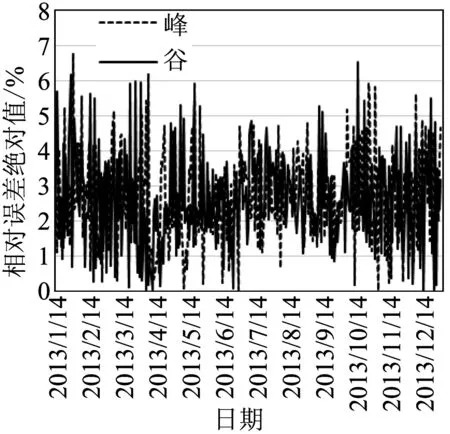
图6　基于k-means和BP网络组合的预测结果相对误差绝对值

3.3两组预测结果的比较与分析

基于上面的结果，对不同预测方法进行了比较，见表3。

表3　不同预测方法的比较

(3)

其中，MAPE为平均绝对值百分比误差。

从表3可以看出，k-means和BP网络组合的方法明星好于BP神经网络的预测方法。

4结语

本文演示了基于K-means和BP神经网络组合模型对用电量的预测。通过本文的实验可以看出，通过K-means和BP网络的组合方法对用电量的预测，可以获得较高的精度，而且还可以有效克服对用电量影响比较大的因素(如：温度)的影响。结论具有实际意义，可为电力部门的日发电需求提供一定的依据。

参考文献：

[1]张庆新，崔展博，马睿，等．基于k-means聚类与径向基神经(RBF)网络的电力系统日负荷预测．科学技术与工程，2013，13(34)：10177-10181．

ZHANGQing-xin,CUIZhan-bo,MARui,etal.Dailyloadforecastingofindustrialenterprisepowersystembasedonk-meansclusteringandRBFneuralnetwork[J]．ScienceTechnologyandEngineering，2013 .13( 34):1017 7-10181.

[2]钱虹，阮大兵，黄正润．电力系统超短期负荷预测算法及应用. 上海电力学院学报，2013，29(1)：9-12.

QIANHong,RUANDa-bing,HUANGZheng-run.Ultra-short-termloadforecastingalgorithmandapplication[J].JournalofShanghaiUniversityofElectricPower, 2013,29(1):9-12.

[3]孙红英．改进的BP神经网络方法在用电量预测中的应用．西安文理学院学报，2007，10(2)：88-91.

SUNHong-ying.ApplicationofimprovedBPneuralnetworkinforecastingelectricityrequirement[J].JournalofXi′anUniversityofArts&Science:NaturalScienceEdition,2007,10(2):88-91.

[4]朱雨晨，加玛力汗水，娜仁花．基于BP神经网络的电力系统短期负荷预测．黑龙江电力，2012，34(6)：439-441，445.

ZHUYu-chen,GamalihanoKumash,Narenhua.Short-termloadforecastingbasedonBPneuralnetworkforelectricpowersystem[J].HeilongjiangElectricPower, 2012,34(6):439-441,445.

[5]WANHe．Deepneuralnetworkbasedloadforecast.COMPUTERMODELLING&NEWTECHNOLOGIES，2014，18(3)：258-262.

[6]熊永胜．基于BP神经网络的电力系统短期负荷预测．成都大学学报，2012，31(2)：167-169.

XIONGYong-sheng.Short-termloadforecastingofpowersystembasedonBPneuralnetwork[J].JournalofChengduUniversity(NaturalScience), 2012,31(2):167-169.

[7]陆柳敏．基于Matlab的电力系统中长期负荷预测及应用．广西电力，2012，35(6)：26-28.

LULiu-min.MediumandlongtermloadforecastingandapplicationbasedonMatlab[J]．GuangxiElectricPower，2012，35(6)：26-28．

[8]祝燕萍，方鸽飞．基于动态自适应神经网络和人体舒适度的短期负荷预测．电力系统保护与控制，2012，40(1)：56-61.

ZHUYan-ping,FANGGe-fei.Short-termforecastingbasedondynamicadaptiveartificialneuralnetworkandhumanbodyamenityindicator[J]．PowerSystemProtectionandControl，2012，40 (1)：56-61．

[9]刘耀年，王卫，杨冬峰．基于模糊划分聚类的中长期用点预测．东北电力学院学报，2004，24(4)：39-42.

LIUYao-nian,WANGWei,YANGDong-feng.Mid-longtermelectriccapacityforecastingbasedonfuzzyclustertheory[J].JournalofNortheastChinaInstituteofElectricPowerEngineering, 2004,24(4):39-42.

[10]马光文，王黎，唐明，等．人工神经网络在用电预测中的应用．四川大学学报，2000，32(2)：25-27.

MAGuang-wen,WANGLi,TANGMing,etal.Powerdemandforecastingbyneuralnetworkmodel[J].JournalofSichuanUniversity(EngineeringScienceEdition), 2000,32(2):25-27.

[11]赵锡平，宋岱，张国庆，等．山东省气温与最大负荷和用电量的关联性分析．电网技术，2004，28(17)：37- 40.

ZHAOXi-ping,SONGDai,ZHANGGuo-qing,etal.Researchoncorrelativityamongairtemperature,maximumloadandpowerconsumptioninshandongpowergrid[J].PowerSystemTechnology,2004,28(17):37-40.

(本文编辑：赵艳粉)

Load Forecast Based on Hybrid Model with k-Means Clustering and BP Neural Network

HUANG Lei1, CHEN Hao2,3, YI Qiao-mu1, TAO Ya-long1

(1.XinnengKaiboIndustrialCo.,Ltd.,Shanghai201210,China;2.SchoolofComputerScience,FudanUniversity,Shanghai201203,China;3.EngineeringResearchCenterofCyberSecurityAuditingandMonitoring,MinistryofEducation,Shanghai200203,China)

Abstract:The development and popularity of the smart grid makes us more aware of the value of power energy resources. As we all konw, electricity cannot be stored, so accurate forecast is of great significance for saving electricity. Because the resident power consumption is affected by many factors, such as weather, the electricity load curve is highly nonlinear, but periodic, and neural network is a very suitable method for establishing the forecasting model. Based on the existing electric power data and methods, this paper presents a hybrid model with the k-means clustering and BP neural network to forecast the electricity load. Compared with the results only using BP network to forecast electricity load, it is concluded that the hybrid method can achieve high precision in forecasting the electricity load.

Key words:electricity load；weather；k-means clustering；BP neural network

DOI：10.11973/dlyny201601012

作者简介：黄磊(1965)，助理工程师，从事电力电子技术，电力用户侧需求研究。

中图分类号：TP399

文献标志码：A

文章编号：2095-1256(2016)01-0056-05

收稿日期：2015-11-13