陀螺式波浪能发电装置浮子运动及载荷分析
2016-07-05周宇英李炳强蔡宗举郑雄波
周宇英,李炳强,蔡宗举,马 勇,张 亮,郑雄波
(1.中国船舶工业系统工程研究院,北京 100036; 2.哈尔滨工程大学 海洋可再生能源研究所,哈尔滨 150001)
陀螺式波浪能发电装置浮子运动及载荷分析
周宇英1,李炳强2,蔡宗举1,马勇2,张亮2,郑雄波2
(1.中国船舶工业系统工程研究院,北京 100036; 2.哈尔滨工程大学 海洋可再生能源研究所,哈尔滨 150001)
摘要:为了获得陀螺式波浪能发电装置浮子的运动规律,运用CFD方法分析浮子在不同波浪工况下的单自由度和两自由度的运动及载荷变化,分析俘获宽度比的变化规律,进行小尺度水槽模型试验,验证波浪条件对装置能量转化的影响,获得装置的共振周期和最大俘获宽度比,通过数值模拟和水槽试验确定该装置浮子的运动规律及载荷变化。
关键词:波浪能发电装置;陀螺式;浮子;计算流体力学;模型试验
海洋波浪能作为一种清洁的可再生能源,具有储藏量大、能流密度大且可预测的优势,已经成为目前最具有开发前景的可再生能源之一[1-3]。根据联合国教科文组织的统计,全球波浪能的理论蕴藏量为30×108 kW。面对储藏量巨大的绿色能源,各国均对此高度重视,开发出多种类型的波浪能发电装置,并取得较好成果。作为摆式波浪能发电装置的代表,由Aquamarine Power公司研制(的第二代“Oyster 800”波浪能发电装置于2012年6月在苏格兰Orkney投入使用,该装置安装宽26 m,铰接在水深为13 m的海床上,离岸距离约为500 m,电能输出值可达800 kW[4]。由Ocean Power Delivery公司研制的“海蛇(pelamis)”波浪能发电装置,是一种离岸式波能转换器,被认为是目前最先进的波浪能发电机组。该装置已经在葡萄牙北海海床上安装并投入使用,可以产生2.2 MW的电能,可以提供约1 500个家庭的用电[5]。国内方面,中国科学院广州能源所研制并进行试验的漂浮式鸭式波能装置[6]和鹰式装置[7]。同时,国家海洋技术中心分别于1992年和2012年研建了重力摆式波浪能发电装置[8]和浮力摆式波浪能发电装置[9],并取得良好的示范运营效果。上述均为摆式波浪能发电装置,主要利用浮子的单自由度运动。陀螺式波浪能发电装置是一种利用陀螺效应的全新的发电装置,着重考虑浮子的2自由度下的运动规律。利用CFD方法分析装置的浮子运动及载荷计算,并依托哈尔滨工程大学波浪水槽,进行小尺度模型水池试验,提供可靠的实验数据,进行可行性分析。
1陀螺式波浪能发电装置
陀螺式波浪能发电装置是一种基于摇荡运动的新型波浪能发电装置,该装置由浮子和陀螺式能量转换机构成,浮子由锚链定位。通过水动力学理论分析和计算,设计浮子的匹配外形和结构,使其在波浪作用下以较大的幅度作摇荡运动。根据陀螺效应,浮子偏转运动时陀螺仪保持水平,引发机械传动机构转动,进而带动发电机发电。
总体设计如图1所示。浮子的剖面为U形,其结构如图2所示,主尺度参数见表1。

图1 总体设计
2浮子运动及载荷的计算方法
2.1力学模型
陀螺式波浪能发电装置由全封闭的浮子和安装于其内部的PTO系统组成。浮子漂浮于水面通过锚系定位。在波浪作用下浮子做6自由度运动,将波浪能转化为浮子的机械能。其中,浮子的纵摇驱动PTO系统做功,将浮子的摇荡动能转化为电能输出。因此,在波浪、PTO系统以及锚系共同作用下浮子的摇荡性能是决定装置吸收波浪能效率的关键因素。下面是进行浮子水动力分析的依据。

图2 浮子的三维图

参数数值长L/m4.0宽d/m1.8直壁高h/m1.0圆弧高m/m0.5吃水/m0.7质量/kg4000.0
根据耐波性原理,浮子在规则波中的纵摇运动方程为
这里,假定浮子的重心G在水线面上,并以此为坐标原点建立空间直角坐标系。
式中:θ(t)——浮子在t时刻的横摇角;
Jθ——浮子绕Z轴的转动惯量;
ΔJθ——浮子纵摇运动引起的周围流体质量对Z轴的转动惯量;

Dhθ(t)——纵摇恢复力矩,纵摇恢复力矩可由流体的浮力的变化,以及锚链的拉伸引起,因为这里锚链的拉伸主要作用是约束浮子的垂荡和纵荡,其对摇荡的作用忽略;
Mθ——浮子的纵摇扰动力矩。
2.2俘获宽度比的计算
入射波的功率为浮子直径宽度内的波浪功率Pi由下式计算。
(2)
式中:H——波高;
T——波浪周期;
D——浮子直径。
浮子的平均吸收功率Pa由下式计算
(3)
式中:Ma——电机作用在浮子上的阻尼力矩;
ω——浮子垂荡角速度,t2-t1=nT,n为整数。
浮子的俘获宽度比定义为浮子平均输出功率与浮子宽度内波浪输入功率之比,可由下式表示。
(4)
3CFD数值模拟
3.1计算工况
由于本装置考虑的适用地区为我国的渤海海域,渤海海浪的特点主要以风生浪为主,浪向与风向有较明显的相关性,冬季浪向以北向为主,夏季南向较多。渤海海浪平均波高分布与渤海波浪平均周期分布见表2、3。

表2 渤海波浪平均波高分布 m
本文根据以上渤海海域的波浪平均波高分布和平均周期,取保守海况要求为波高为0.7 m,周期3~7 s。根据实际计算量的安排,选取波浪周期为3 s和4 s的2个工况,浮子运动可分为只有一个自由度的纵摇运动和2个自由度的纵摇加垂荡运动。改变等效外界PTO阻尼系数,得出浮子的PTO阻尼与俘获宽度比曲线,以及浮子的垂向力、纵摇力矩、纵摇角和纵摇角速度时历曲线。即:
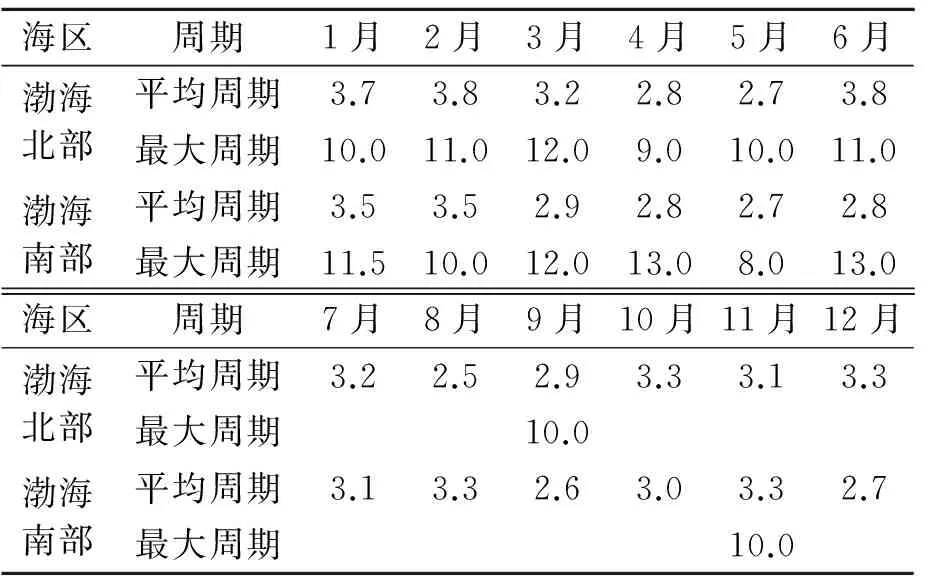
表3 渤海波浪平均周期分布 s
1) 按波浪周期划分。波高0.7 m、波浪周期为3 s和4 s 2种波浪参数对比。
2) 按浮子运动自由度划分。单自由度的纵摇运动和纵摇垂荡2自由度的耦合运动。
3) 按外界参数划分。浮子只有纵摇运动时,阻尼系数变化范围为0~28 000 N·m·s/rad;浮子有纵摇和垂荡2自由度时,其外界弹性系数范围为0~240 000 N/m,阻尼系数为80 kN·m·s/rad。
3.2CFD计算设置
3.2.1流体域划分
根据给定模型,将三维实体模型简化为二维模型,将模型长度方向尺度减小,二维计算域厚度为0.05 m,长度为14 m,高度为6 m,选取水深为3 m,浮子质量为50 kg,吃水0.7 m,初定其绕Z轴惯量为7 kg·m2,计算域如图3所示。

图3 计算域示意
图3a)中坐标系为计算域的总体坐标系,采用推板造波,造波板位于x=0处,生成规则波,波浪沿X轴负方向传播,Y方向为波高方向,Z为浮子长度方向。浮子域如图3 b)所示,图中坐标系为浮子的坐标系,浮子可在Y方向做垂荡运动,绕Z方向转动。
3.2.2网格划分
计算域网格划分见图4,采用结构网格,计算域网格数目约31 000,浮子域内网格约8 000。

图4 计算域网格划分示意
3.2.3边界条件的设置
边界条件的设置见图4,图中双向箭头表示该处边界条件为Opening,XY平面设置为Symmetry,其余边界条件设置为Wall。按照上述设置既可以减小计算时间,又可保证计算精度。
3.2.4求解控制
对浮子采用刚体求解,其刚体收敛控制分为运动控制、力的控制和力矩控制。其收敛标准见表4。
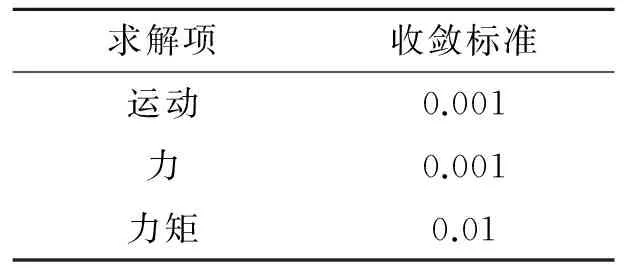
表4 收敛标准
3.3计算结果分析
3.3.1纵摇运动
浮子仅有单自由度的纵摇运动,其纵摇旋转轴在水线面下0.2 m。运用CFX软件模拟纵摇阻尼系数为0、800、1 600、2 400、3 200、4 000、5 600、8 000、12 000、16 000、20 000、24 000和28 000 N·m·s/rad下的浮子的纵摇运动。选取了浮子在波高为0.7 m,波浪周期为3 s时,纵摇阻尼系数为4 000和8 000 N·m·s/rad时运动和受力对比,见图5。
图5 a)为浮子的垂向受力曲线,垂向力指水给浮子的垂向力,包含静力和动力,静力指浮子在静水中的浮力,根据水线位置确定浮子静浮力为40 000 kN,图中可以看出不同纵摇阻尼系数下的浮子垂向受力曲线基本重合,这说明纵摇阻尼系数的改变对浮子的垂向受力影响不大。
图5 b)为浮子受波浪力矩的时历曲线。由图可见,纵摇阻尼系数较大时,浮子所受到的波浪力矩也越大,这是由于纵摇阻尼越大,浮子纵摇角越小,其对波浪的响应越小,与波面位置相差越大,其波浪力矩也就越大。
图5 c)和图5 d)分别为浮子的纵摇角时历曲线和纵摇角速度时历曲线,纵摇阻尼较大时,其纵摇角较小。原因是纵摇阻尼系数越大,浮子纵摇运动时克服外界做功越多,浮子自身能量减少,转动速度下降,位移也相应减小。

图5 T=3 s时,浮子的受力及运动
图6为在波浪周期为3 s时,浮子在不同纵摇阻尼下的俘获宽度比。由图6可知,纵摇阻尼系数会对俘获宽度比产生很大影响。此时,俘获宽度比的最大值为0.29,对应的最佳阻尼系数为5 600 N·m·s/rad,其平均输出功率为1.3 kW。
图7为浮子在波高为0.7 m,波浪周期为4 s时,纵摇阻尼系数为4 000和8 000 N·m·s/rad时运动和受力对比。

图6 T=3 s时,浮子不同纵摇阻尼下的俘获宽度比曲线
从图7 a)可见,浮子在周期为4 s的波浪中不同纵摇阻尼时的垂向受力基本相同,但力的幅值较波浪周期为3 s时大。不同纵摇阻尼下浮子所受波浪力矩不尽相同,纵摇阻尼较大时其所受波浪力矩也较大,这与波浪周期为3 s时的规律一致。对于较大的纵摇阻尼,浮子纵摇时对应的能量消耗也较大,使其纵摇角和角速度都较小。

图7 T=3 s时,浮子的受力及运动
图8为T=4 s时,浮子不同纵摇阻尼下的俘获宽度比。

图8 T=4 s时,浮子不同纵摇阻尼下的俘获宽度比
图8中的俘获宽度比随阻尼系数变化的趋势
与图6相同,但浮子的最大俘获宽度比略有不同,图15中俘获宽度比最大值为0.29,图8中的俘获宽度比最大值为0.297,但两者的最大俘获宽度比对应的最佳阻尼相同。
3.3.2纵摇加垂荡运动
装置有2个自由度时,需要用锚链将其固定,浮子以纵摇运动为主,尽量减小垂荡幅值,波浪周期为3 s时,取弹性系数为16 000和40 000 N/m的2种工况下浮子的受力及运动对比,结果见图9、10。
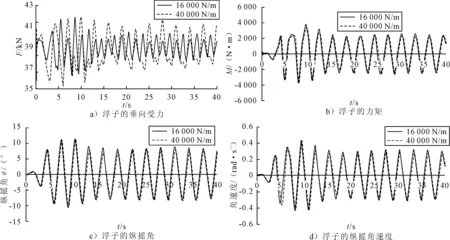
图9 T=3 s时,浮子的受力及运动
从图9 a)可见,弹性系数较大时,浮子的垂向波浪力也较大,这是由于弹性系数越大时,浮子的在垂荡时克服外界做功越大,自身动能减小,垂荡位移相应减小,吃水增加,垂向力增大;从图9 b)可见,弹性系数为40 000 N/m时,浮子所受的波浪力矩略小于弹性系数为16 000 N/m,这说明弹性系数的改变对浮子所受的波浪力矩影响很小;从图9 c)和图9 d)可见,弹性系数较小时,其纵摇角和角速度较大,但弹性系数的改变对浮子纵摇性能的影响很小。
波浪周期为3 s时,俘获宽度比随弹性系数的变化见图10,取纵摇阻尼系数8 000 N·m·s/rad,由图4可见,俘获宽度比随着弹性系数的增加呈现先减小后基本不变的趋势,在弹性系数为0,即浮子垂荡不受限制时,俘获宽度比为最大。在弹性系数大于80 000 N/m时,俘获宽度比基本不变。对比于浮子只有纵摇运动时,浮子在有垂荡运动时的俘获宽度比较高。

图10 T=3 s时,浮子在不同弹性系数下的俘获宽度比
波浪周期为4 s时,取弹性系数为16 000和40 000 N/m的2种工况对浮子的受力及运动对比,结果见图11。
从图11 a)可见,弹性系数较大时,其垂向力也较大。相比浮子在波浪周期为3 s的波况下的受力幅值较大;相比浮子只有纵摇运动时力的幅值较小,这是由于浮子有垂荡运动时,浮子可以随波面起伏,其设计水线与波面位置相差不大,使其垂向力也较小。而图11 b)~图11 d),浮子在周期为4 s的波浪中运动时,其力矩、纵摇角和纵摇角速度随弹性系数变化的规律与波浪周期为3 s时一致,但幅值比波浪周期为3 s时略大。
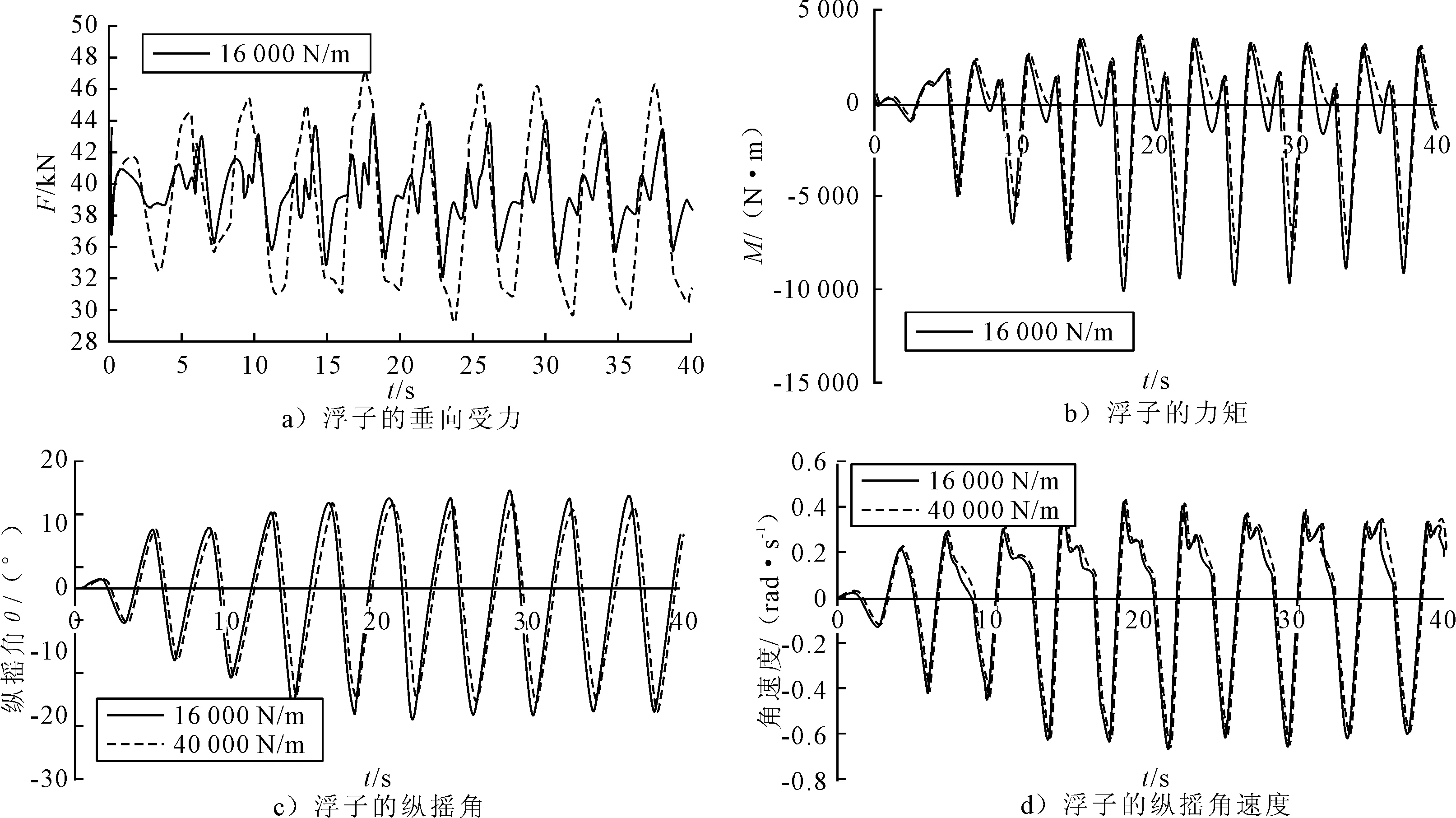
图11 T=3 s时,浮子不同纵摇阻尼下的俘获宽度比
当波浪周期为4 s时,俘获宽度比随弹性系数的变化见图12,从图中可以看出,俘获宽度随比着弹性系数的增大而减小,在弹性系数大于临界值时,俘获宽度比基本不变。这与波浪周期为3 s时俘获宽度比随弹性系数变化的规律一致,但俘获宽度比较大。

图12 T=4 s时浮子在不同弹性系数下的俘获宽度比
4水槽试验
结合以上的基于CFD方法计算获得的计算数据,设计了陀螺式波浪能发电装置的小尺度模型试验,用以验证浮子的运动及受力载荷。试验是在哈尔滨工程大学波浪水槽中进行。
4.1试验装置
波浪水槽:长33.5 m、宽0.8 m、深1.0 m,水深0.2~0.6 m,为钢骨架玻璃壁面、底面结构,采用单板拉推式造波机造波,可生成规则波和不规则波。规则波生成波高范围0.03~0.25 m,周期0.5~5.0 s;不规则波可根据PM谱、ITTC单参数谱、ITTC双参数谱、沿海谱和自定义谱生成。池端设有二级消波装置,一级为大孔径消波网板,一级为小空隙消波网,池中多点设有浪高仪,实现波高测量的同时,还可分析反射波作用的影响。
浪高仪。安装在水槽上方,用于对波浪进行实时测量。
电阻箱。作为发电机输出负载。
角位移传感器。测量浮子和摆锤的角位移、角速度、角加速度时历曲线,仪器的精度直接关系到试验结果的准确度,因此选用了精度等级较高的型号JN338,精度0.5%。
应变片。测量浮子在波浪作用下沿浪向的受力。采用BF120-5AA型号的箔式应变片,精度K=2.20。
4.2试验模型
根据原型装置的主尺度以及水池的尺度,本次实验的缩尺比为10∶1。实验模型主要包括箱型浮子、摆锤,以及发电机。
1) 浮子。雪弗板结构,长0.8 m,宽0.18 m,深0.15 m。浮子横剖面为U形,上部为直立侧壁,高0.1 m,底部由圆弧连接,高0.05 m,浮子采用等截面型式。
2) 摆锤。质量0.5 kg,连杆长度11.5 cm,摆锤及连杆均为钢制结构,连杆质量0.1 kg。
3) 大转矩直流发电机。发电机采用标准直流发电机,最大输出电压为DC18 V,最大输出电流为500 mA,最大输出功率为5 W,工作最大转速6 000 r/min,电机直径为37.5 mm,机身长度为50 mm,电机轴长75 mm,电机轴径3.17 mm,电机直径最大37.5mm,电机重量196.68 g。
4.3试验方法与步骤
1)选取一组模型参数(模型重心位置;浮子转动中心位置;摆锤质量、转动轴高度、杆长)。
2)完成模型组装,调整模型使其达到指定参数,安装好的模型如图13所示。
3)将调整好的陀螺式波浪能发电装置模型安装在水槽上方,调节滑杆在滑道内的位置,使浮子转动中心达到指定高度,如图14所示。
4)通过调整压载改变浮子浮态,使得浮子的浮心位置到达指定位置。
5)启动造波板使其持续产生指定波高和周期的规则波。
6)记录相应数据。

图13 模型安装

图14 试验布置
4.4试验结果
试验参数见表4,由于是小尺度水池试验,并根据水池造波能力,选取波高为0.04和0.06 m两种波况对浮体的纵摇运动进行对比。

表4 试验参数
纵摇幅值对比见图15~22。

图15 浮子纵摇角时历曲线
由图15可见,波高为0.04 m时,浮子的纵摇角在15°左右;波高为0.06 m时,浮子的纵摇角在18°左右。这说明波高的增大有利于浮子纵摇幅值的增大。

图16 摆锤纵摇角时历曲线
由图16可见,波高为0.04 m时,摆锤的纵摇角在6°左右;波高为0.06 m时,摆锤的纵摇角在8°左右。这说明波高的增大有利于摆锤纵摇角的增大。

图17 相对纵摇角时历曲线
相对纵摇角是浮子相对于摆锤的纵摇角,在装置做纵摇运动时,浮子和摆锤同时运动,但存在相位差,使相对纵摇角增大。由图17可见,波高为0.04 m时,相对纵摇角在20°左右;波高为0.06 m时,相对纵摇角在27°左右。这说明波高的增大有利于相对纵摇角的增大。
纵摇角速度对比见图18~20。
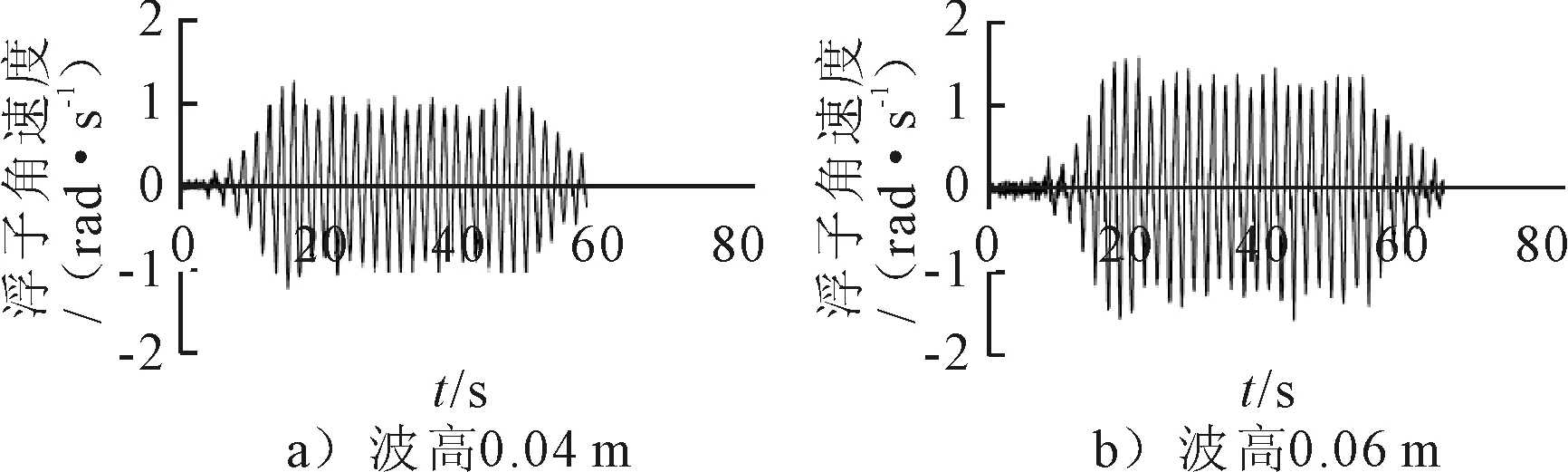
图18 浮子纵摇角速度时历曲线
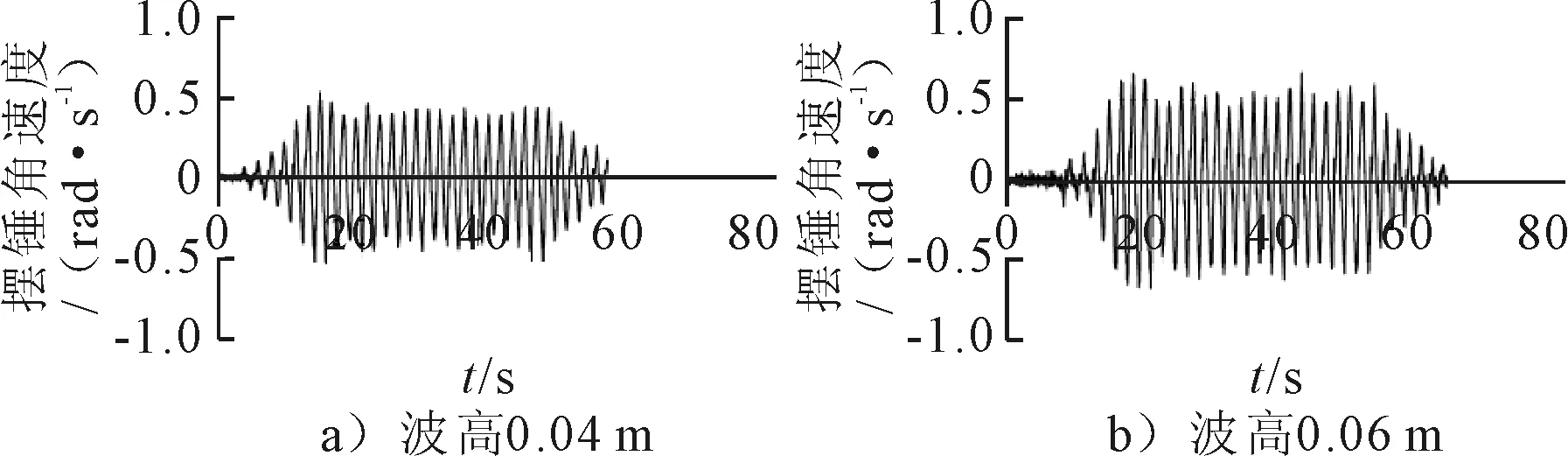
图19 摆锤纵摇角速度时历曲线

图20 相对纵摇角速度时历曲线
相对纵摇角速度是浮子相对于摆锤的纵摇角速度,它是影响装置能量输出的重要因素,在装置做纵摇运动时,浮子和摆锤同时运动,两者角速度存在相位差,使有效纵摇角增大。可以看出,波高为0.04 m时,相对纵摇角速度在1.5 rad/s左右;波高为0.06 m时,相对纵摇角在2.0 rad/s左右。这说明波高的增大有利于相对纵摇角速度的增大。
根据水池造波能力,选取波浪周期为1~3 s的波况,相对纵摇角随波浪周期变化见图21。

图21 相对纵摇角随波浪周期变化
由图21可见,相对纵摇角随着波浪周期的增大先增大后减小,在波浪周期为1.8 s时出现峰值,这说明对于确定参数的装置其共振周期几乎不变。

图22 装置俘获宽度比随波浪周期变化
从图22中可以看出,装置的俘获宽度比在波浪周期为1.8 s时最大,向两侧递减。波高较大时,其俘获宽度比略大,最大值为0.377。这说明靠近共振周期有利于装置对能量的吸收。
5结束语
运用CFD方法,对陀螺式波浪能发电装置的浮子在不同波浪条件下进行模拟。当其在纵摇单自由度下运动时,纵摇阻尼系数的改变对垂向受力影响不大,在波高一致时,俘获宽度比对应的最佳阻尼基本相同; 在纵摇加垂荡两自由度下运动时,弹性系数的改变对浮子所受的波浪力矩和纵摇性能均有较小的影响,当弹性系数为0时,此时的俘获宽度比最大;当弹性系数到达某一临界值时,俘获宽度比基本不变。
在小尺度水池模型试验中,随着波高的增加,浮子的总要幅值随之增大,决定装置能量转化效率的相对纵摇角也随之增大。相对纵摇角随着波浪周期的增大先增大后减小,在所测试的波高下,此峰值出现在周期为1.8 s时。当周期为1.8 s时,俘获宽度比出现峰值。这说明靠近共振周期有利于装置对能量的吸收。
本文通过数值模拟和试验测试相结合的方法,论证了陀螺式波浪能发电装置作为一种新型的波浪能发电装置的可行性,结果表明该装置具有能量转换效率高、系统可靠性高、主体结构简单等特点。后续研究方向应为研制模型和实型样机,完成相关海况海试,为开发适合我国波浪能资源特征的工程样机的开发和应用进一步研究设计方法、关键技术和评价基础。
参考文献
[1] 刘美琴,郑源,赵振宙,等.波浪能利用的发展与前景[J].海洋开发与管理,2010,27(3):80-82.
[2] 游亚戈,李伟,刘伟民,等.海洋能发电技术的发展现状与前景[J].电力系统自动化,2010(14):1-12.
[3] 蔡男,王世明.波浪能利用的发展与前景[J].国土与自然资源研究,2013(6):92-94.
[4] WHITTAKER T, COLLIER D, FOLLEY M, et al. The development of Oyster-a shallow water surging wave energy converter[C].Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal. 2007:11-14.
[5] HENDERSON R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter[J]. Renewable energy, 2006,31(2):271-283.
[6] 盛松伟.漂浮式鸭式波浪能发电装置研究[D].广州:中国科学院广州能源研究所,2011.
[7] 张亚群,盛松伟,游亚戈,等.100 kW一基多体漂浮鹰式波浪能发电装置模型试验研究[J].海洋技术学报,2014(4):13.
[8] 郑雄波,张亮,马勇.双浮体波能装置的水动力计算与能量转换特性分析[J].科技导报,2014,32(19):26-30.
[9] 顾明浩,谭祺,石世宁,等.摆式海洋波浪发电原理与事例[J].流体传动与控制,2012(5):5-9.
Study on Motion and Load of the Floater in Top-shaped Wave Power Generation Device
ZHOU Yu-ying1, LI Bing-qiang2, CAI Zong-ju1, MA Yong2, ZHANG Liang2, ZHENG Xiong-bo2
(1 Systems Engineering Research Institute, Beijing 100036, China;2 Institute of Ocean Renewable Energy System, Harbin Engineering University, Harbin 150001, China)
Abstract:The motion mechanism of the floater top-shaped has been studied by CFD methods. The movement and load changes in single and two degrees of freedom are given under different wave conditions, and the law of capture width ratio changes is analyzed. The small scale model test is carried out in tank, to prove the influence of different wave conditions on the energy conversion device. Based on the numerical simulation and tank test, the motion mechanism and load changes of the floater are confirmed.
Key words:wave power generation device; top-shaped; floater; CFD; model test
DOI:10.3963/j.issn.1671-7953.2016.03.022
收稿日期:2015-11-13
基金项目:国家自然科学基金(11572094)
第一作者简介:周宇英(1968—),男,硕士,高级工程师 E-mail:zhouyy_bj@139.com
中图分类号:U665
文献标志码:A
文章编号:1671-7953(2016)03-0090-09
修回日期:2015-12-11
研究方向:船舶电力系统、海洋波浪能发电及分布式能源系统等
