装备经济寿命的一般规律研究

吴诗辉，　刘晓东，　郭亚坤，　杨闽湘

(1. 空军工程大学 装备管理与安全工程学院， 陕西 西安 710051；　2. 95876部队)

装备经济寿命的一般规律研究

吴诗辉1，刘晓东1，郭亚坤2，杨闽湘1

(1. 空军工程大学 装备管理与安全工程学院， 陕西 西安 710051；2. 95876部队)

摘要为研究装备经济寿命的变化规律，需要对装备经济寿命进行解析求解。经典的经济寿命模型未给出解析解，而是采取列表试算法，难以对经济寿命的影响因素进行分析。通过引入Lambert W函数，将装备经济寿命表示成影响因素的显式方程；在此基础上，分析了各影响因素对经济寿命的影响规律，归纳出提高经济寿命的方法。同时，为实现经济效益最大化，提出了最佳使用维修费增长率的概念，并给出了解析公式计算最佳使用维修费增长率的取值区间。算例验证表明，分析结论正确。

关键词经济寿命；Lambert W函数；解析解；影响规律

装备经济寿命是从经济角度看装备最合理的使用期限。对于军事装备，与生产设备不同，谈不上经营的经济效益，用年费用法求其经济寿命更加适宜。因此，在研究经济上合理的使用期限(即经济寿命)时，就是找出装备年平均费用最低的年份，一般利用经典经济寿命计算模型，采取列表法试算[1]75。

文献[2]分别研究了原型装备更新和出现新装备条件下的更新决策方法，引入价值损耗描述技术进步对装备更新决策的影响，给出了经济寿命的计算公式，但没有考虑资金的时间价值。文献[3]考虑了资金的时间价值、装备的残值，应用年均费用法，建立了装备经济寿命的数学模型。为了增强模型的适用性，许多学者对经典经济寿命计算模型进行了改进。文献[4]认为在较长时期内，年利率和物价上涨指数受各种因素的影响，是一个以某个数值为基准上下浮动的不确定值，因此用模糊数表示贴现率对经济寿命进行了研究。文献[5]利用灰色理论，根据已发生的使用维护费、残值对未来的费用作出预测，在此基础上进行了装备经济寿命分析。

从现有文献看，目前大多数学者仍以经典经济寿命模型为基础展开研究，即采取列表法试算经济寿命[4-7]，但是试算法相比解析法，难以发现影响经济寿命的内在规律。本文利用Lambert W函数推导了装备经济寿命的精确解析解，在此基础上，研究了装备经济寿命的变化规律，对其影响因素进行了分析，提出了最佳费用增长率的概念，并给出了提高装备经济寿命的建议，为装备更新决策提供了一种新的思路。

1装备经济寿命的数学模型

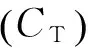
现金流量图如图2所示。

可算得购置费年分摊为

式中，K0表示购置费；L表示装备残值；i表示年利率；n表示年份；A表示资金的等额年值;P表示资金的现值;F表示资金的终值。

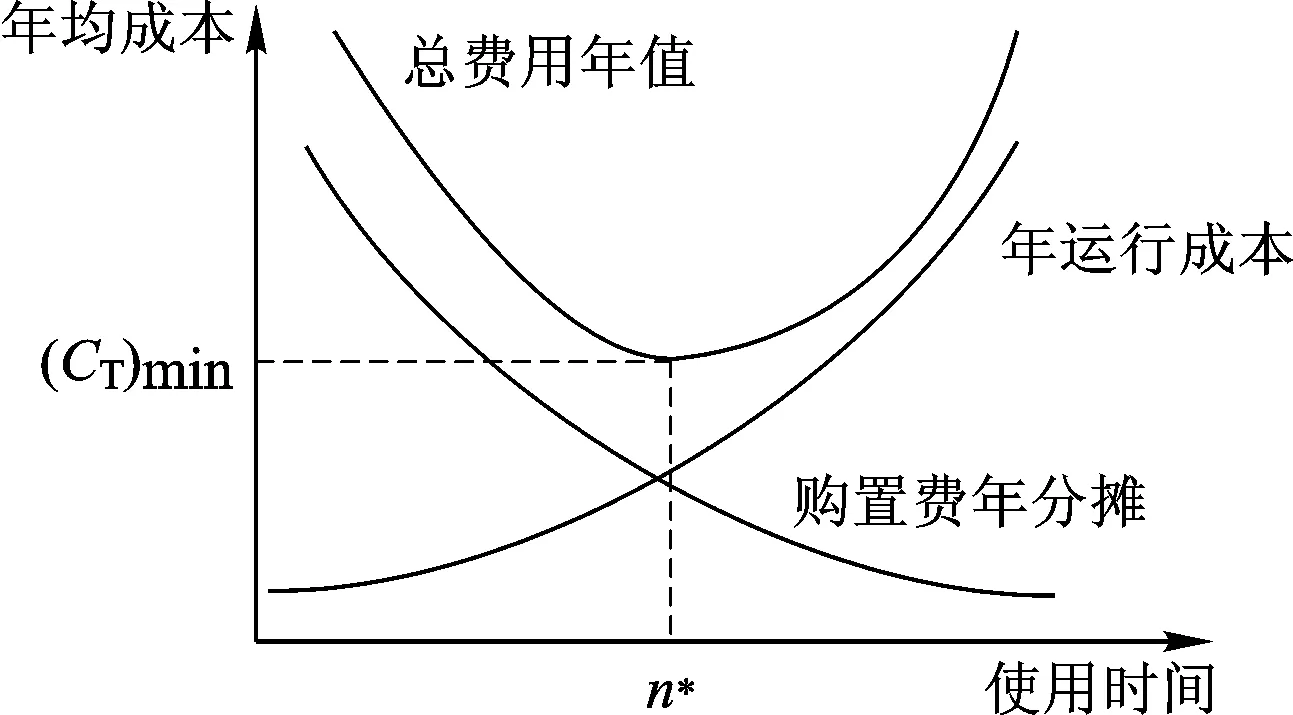
图1　年均成本与装备使用时间的关系

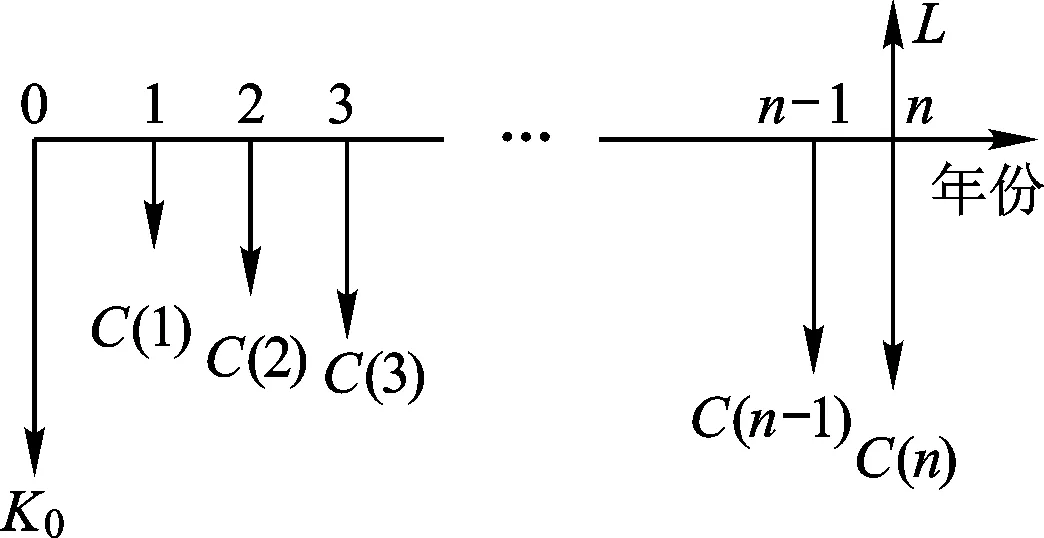
图2　现金流量图

使用维修费年分摊为

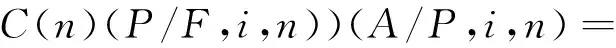
式中，C(j)表示第j年的使用维修费。

总费用的年分摊为

(1)

CT最小时，得到的n即为装备的经济寿命。

假设不考虑残值，每年使用维修费增长幅度均为ΔC,即C(j)=C(1)+(j-1)ΔC,经济寿命的数学模型为

(2)

2模型的解析解

公式(2)可转化为

其中的求和项

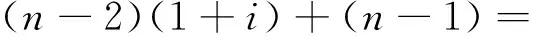
(3)

该式括号内是一个数列的求和项，令a=1/(1+i)，利用错位相减法进行求和计算。公式(3)方括号内可表示为

两端同乘以a，

aSn=a2+2a3+3a4+…+(n-1)an

故

从而有

(4)

故由式(3)、式(4)，可得

从而

令

有

ΔCni(1+i)nln(1+i)+ΔC(1+i)nln(1+i)-

令上式左端分子等于0，并约去i(1+i)n,得：

-K0iln(1+i)-ΔC+

化简，

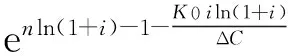
注意到，等式左侧为Lambert W函数形式，则上式可改写为

从而，可解得经济寿命的精确解

(5)

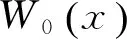
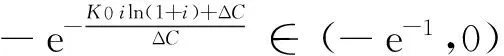
图3　Lambert W函数在(-e-1,0)区间上的部分

Lambert W函数在(-e-1,0)区间上的特性：

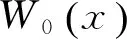
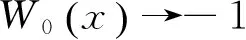
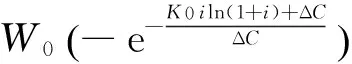
3装备经济寿命的一般规律分析

3.1影响因素分析

从式(2)可看出，经济寿命主要取决于K0,i,C(1),ΔC 4个因素。观察公式(5)，找出经济寿命与4个因素之间的影响关系。

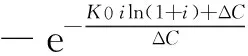
2) n*不随第一年的使用维修费C(1)的变化而变化。

3) n*可转化为

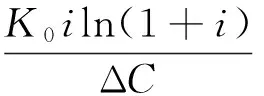
从定性角度可解释为，随着使用维修费增幅ΔC的增大，补偿购置费年分摊下降趋势所需的时间缩短，即经济寿命缩短。

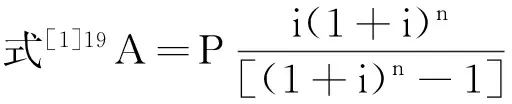
3.2设计最佳的费用增长率

根据3.1节的分析，经济寿命随使用维修费的增幅单调递减，这意味着，要提高经济寿命，需要压缩使用维修费的增幅。然而，经济寿命并不是越大就越好，当经济寿命小于自然寿命时，如果装备使用不到自然寿命末期而按经济寿命更新，则装备自然寿命的潜力没有得到充分地利用；经济寿命大于自然寿命时，会对使用维修费的增幅大幅压缩，造成使用维修费无法满足装备使用需求。因此，最佳状态是合理设计使用维修费的增幅，使经济寿命和自然寿命相等。

因此，由公式(5)，令

其中，N表示自然寿命。

可解得

(6)

也可表示为

(7)

(8)

3.3装备经济寿命的一般规律

综上分析，通过严格的数学推导和证明，可归纳总结出装备经济寿命的一般性规律：

1) 对于公式(2)描述的经济寿命模型，必然存在一个经济寿命的实数解。这是由于一般情况下，K0>0,ΔC>0,i>0成立，结合公式(5)和LambertW函数特性可得出此结论，这在第2节中进行了证明。

2) 装备的经济寿命与购置费K0、年利率i、使用维修费年增幅ΔC等因素相关，而与第一年的使用维修费C(1)无关。其中，经济寿命随购置费K0的增大而增大，随年利率i的增大而增大，随使用维修费增幅ΔC的增大而缩短。特别是，当ΔC=0,即各年使用维修费始终保持不变时，此时经济寿命趋于无穷大。

3) 要提高装备的经济寿命，可以通过提高购置费K0，增大年利率i，降低使用维修费增幅ΔC等方法实现，但是考虑到提高购置费和增大年利率的方法不切实际，因此，提高装备的经济寿命应该通过降低使用维修费增幅来实现。一般可以通过2种途径来降低使用维修费增幅，提高经济寿命：一是在设计阶段，使装备具有较高的可靠性，从而降低故障率，使各年的使用维修费保持慢速增长；二是在使用阶段，通过采用表面工程等新技术，可以减缓使用维修费用增长的幅度，达到延长经济寿命和自然寿命的目的。

4) 最佳的经济寿命并不意味着经济寿命越长越好，只要装备的经济寿命与自然寿命相当，则装备的自然寿命就能够得到充分发挥，此时装备具有最佳的经济效益。为此，在控制使用维修费增幅ΔC时不必使其接近于0(实际上也是很难做到的)，而是存在一个最佳的增幅：如果购置费与使用维修费年增幅的比例保持在最佳比例(由公式(7)算得)，或将使用维修费年增长率控制在最佳增幅(由公式(8)算得)，则可实现装备经济效益的最大化。

4实例计算

例某型飞机购置费为500万元，第1年的使用维修费50万元，以后每年递增5万元，残值为0元，年利率为10%，自然寿命为25a，对经济寿命进行分析。

对4个因素分别进行单因素敏感性分析，假设购置费K0取值范围为(300～700)万元，年利率i取值范围为0.01～0.2，使用维修费C(1)取值范围为(30～70)万元，维修费增幅ΔC取值范围为(1～20)万元，观察经济寿命的变化情况，如图4所示。可见，图中经济寿命的变化趋势与3.1节分析的结论相同。

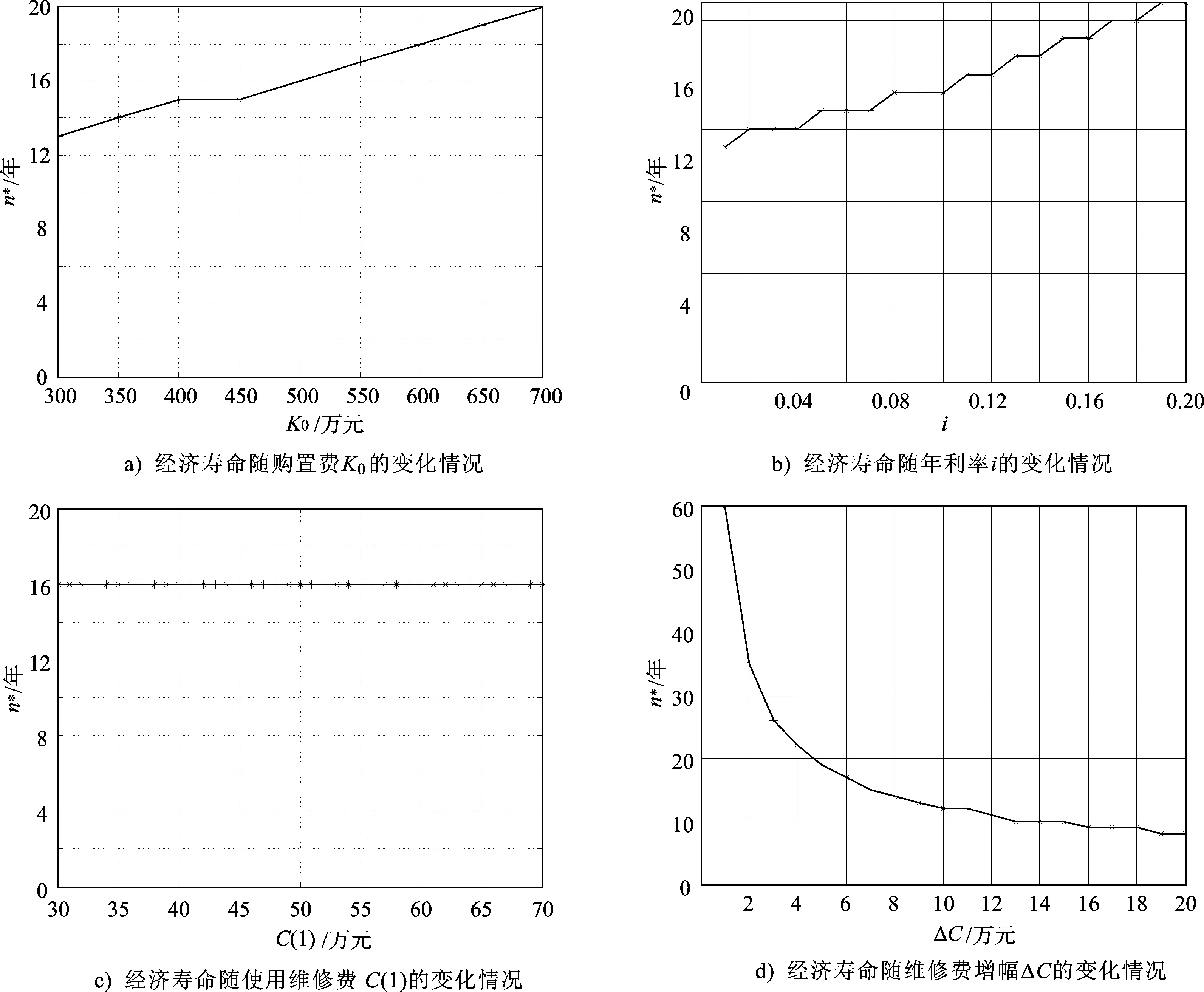
图4　4种影响因素取不同值时经济寿命的变化情况

对于该问题，根据公式(8)还可以计算出最佳费用年增幅为(3.157 ～3.328)万元，此时经济寿命刚好等于25a。

5结 束 语

本文利用LambertW函数，推导了装备经济寿命的解析计算公式，在此基础上，对经济寿命的影响因素及其变化规律进行了分析。由于经济寿命的最佳取值等于自然寿命，提出经济寿命最佳使用维修费增长率的概念。最后，根据影响规律分析，提出了提高经济寿命的建议。但文中结论是在假设年增幅相同的情形下得出的，对于年增幅不同的情形，如果假设3～5a为一个周期，该周期内的年增幅取平均值，而每个周期之间增幅保持恒定，则也可近似满足文中的假设条件，因此，本文的研究具有一般性。但是，对于部分装备的使用维修费随着使用时间增加，不满足单调递增规律的情形，则还有待进一步研究。

参考文献(References)

[1]赵建华，高风彦. 技术经济学[M].2版.北京：科学出版社，2004.

[2]夏水春，李梅. 后勤装备更新的技术经济分析[J].装备指挥技术学院学报, 2003,14(6):16-19.

[3]白利军，王永智，郜鹏，等.武器装备经济寿命分析与研究[J].火力与指挥控制, 2013,38(1):111-113.

[4]董岳，花兴来，李贻铭. 运用模糊理论的雷达装备经济寿命建模与分析[J].空军雷达学院学报, 2005,19(4):50-52.

[5]王春健. 灰色理论在装备经济寿命预测中的应用[J].兵工自动化,2007(4):21-23.

[6]方辉，宋忠平，李莉. 后勤装备经济寿命预测模型与分析[J].军事经济研究,2012(3): 41-42.

[7]张丽叶，邢伟. 装备更新经济性分析[J].装备学院学报,2012, 23(5):36-39.

[8]CORLESSRM，GONNERGH.OntheLambertWfunction[J].AdvancesinComputationalMathematics,1996,5(1):329-359.

(编辑：李江涛)

Research on General Rules of Economic Life for Weapons and Equipments

WU Shihui1，LIU Xiaodong1，GUO Yakun2，YANG Minxiang1

(1. Equipment Management and Safety Engineering College, Air Force Engineering University, Xi’an Shaanxi 710051, China;2. 95876 Troops, China)

AbstractIn order to study the rules of change of equipment economic life, it is necessary to find an analytical solution. Classical economic life models just adopt tabulation trial method instead of analytical solution, so it is impossible to analyze the influencing factors of the economic life. By introducing Lambert W function, the paper expresses the equipment economic life as an explicit equation; based on above work, the paper analyzes the influencing rules of each influencing factor on the economic life and accordingly concludes a way to improve economic life. At the same time, for maximize the economic benefit, the paper brings out a concept of the repair cost growth rate under the best utilization and gives an analytical equation to find out the value range of repair cost growth rate under the best utilization. The verification result of the example shows that the analysis conclusion herein is correct.

Keywordseconomic life; Lambert W function; analytical solution; influencing rules

收稿日期2015-05-11

作者简介吴诗辉(1982—)，男，讲师，博士，主要研究方向为装备经济。wu_s_h@163.com

中图分类号F224.9

文章编号2095-3828(2016)03-0063-06

文献标志码A

DOI10.3783/j.issn.2095-3828.2016.03.013